公路兼城市道路桥梁抗震设计对比分析
2021-11-12刘其卓
■刘其卓
(福建省交通规划设计院有限公司,福州 350004)
1 工程概况
晋江某大道位于晋江以南, 路线经过晋江市区、安海镇、南安水头镇,作为贯穿晋江市东西向的主要干道,承担着晋江市的集疏运功能。 项目采用一级公路兼城市快速路的技术标准进行设计,主线双向八车道,设计速度80 km/h,道路红线宽70 m(含辅道),道路全长约5.5 km,其中设置桥梁2 687 m/6 座,桥梁采用分离式断面形式,单侧桥宽17 m,中央绿化带6.5 m,标准跨径采用35 m 预制小箱梁,下部结构采用1.6 m×1.6 m 的矩形双柱墩,基础采用4 根桩径1.6 m 的钻孔灌注桩, 桥梁标准横断面布置见图1。
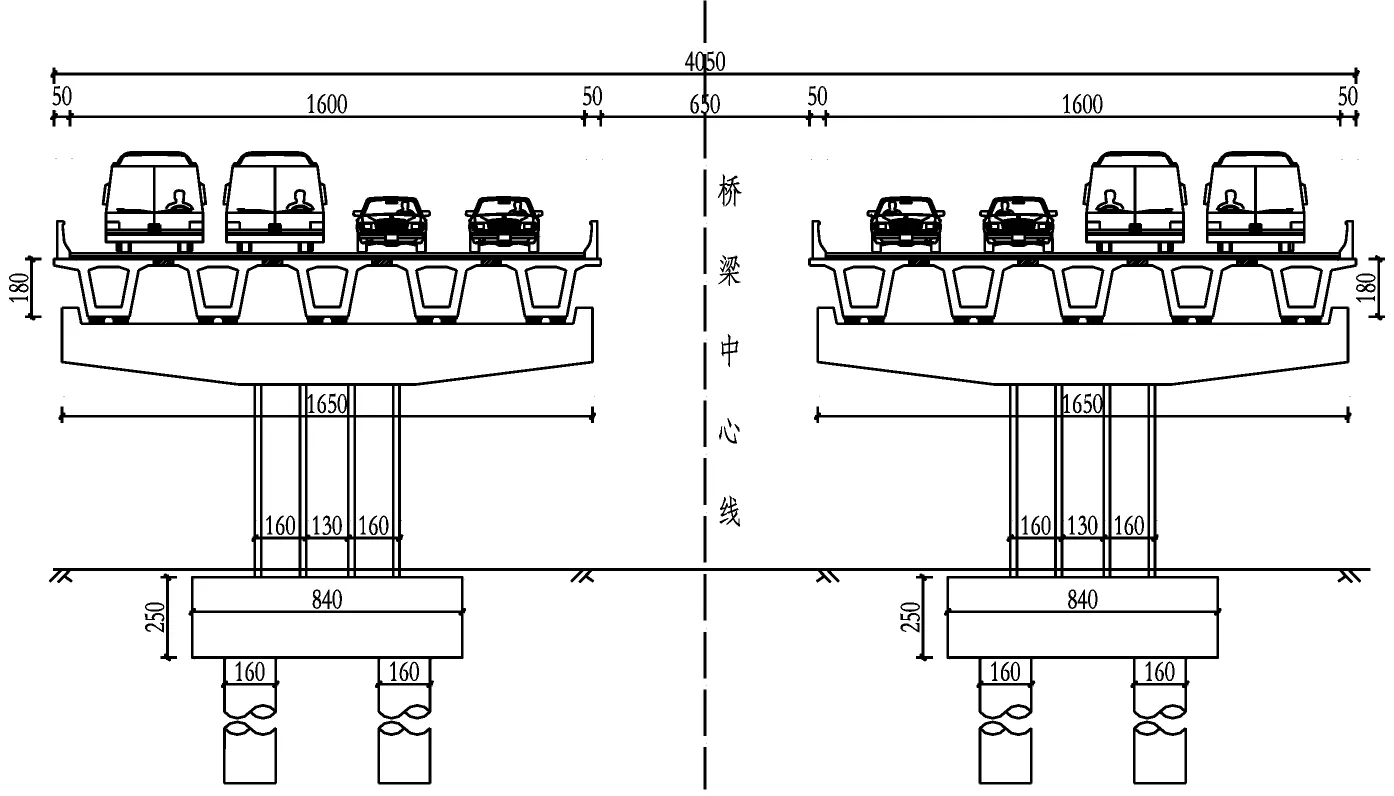
图1 桥梁标准横断面
1.1 主要技术标准
(1)道路等级:一级公路兼城市快速路;(2)设计速度:设计速度80 km/h;(3)荷载等级:公路-Ⅰ级(城市-A 级校核);(4)设计基准期:100 年;(5)结构安全等级:桥梁结构为一级;(6)环境类别:Ⅰ类。
1.2 地质条件
拟建场地内岩层地质由上往下分布地层为第四纪人工填土、冲洪积层、坡残积层、燕山早期侵入花岗岩。
1.3 地震参数及抗震设计要求
依据《中国地震动峰值加速度区划图(GB 18306-2015)》、《公路桥梁抗震设计规范(JTG/T 2231-01-2020)》[1]及《城市桥梁抗震设计规范(GJJ 166-2011)》[2]的相关规定,并结合本项目的技术标准及桥梁的标准跨径形式,得出地震参数及抗震设计要求(表1)。
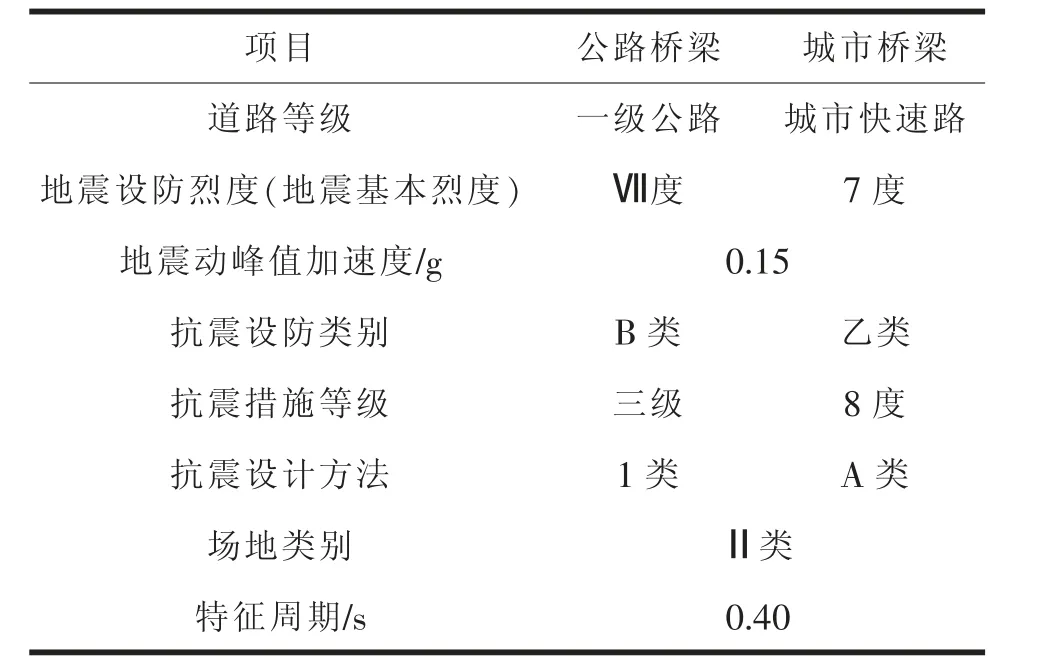
表1 地震参数及抗震设计要求
2 抗震性能设计标准介绍
地震作用主要采用设计加速度反应谱和设计地震动时程两种方法来表征,本文采用设计加速度反应谱的方法来计算地震作用, 并进行抗震分析。本项目桥梁抗震设防类别不论是公路桥梁的B 类,还是城市桥梁的乙类, 均采用两水准抗震设防,即E1 地震作用对应于第一级设防水准,E2 地震作用对应于第二级设防水准。
2.1 地震作用

2.1.1 公路桥梁抗震设计标准
本项目道路等级在公路中定义为一级公路,依据《公路桥梁抗震设计规范》:水平向设计加速度反应谱S 取值情况如下:
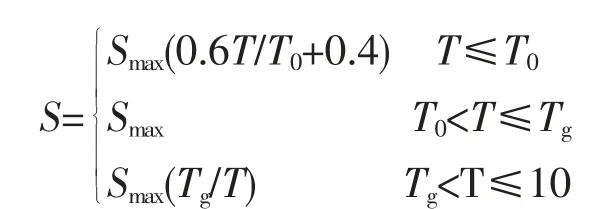
式中:T 为周期(s);T0为反应谱直线上升段最大周期,取0.1s;Tg为特征周期(s);Smax为设计加速度反应谱最大值(g)。
其中反应谱最大值Smax为:Smax=2.5CiCsCdA
式中:Ci为抗震重要性系数;Cs为场地系数;Cd为阻尼调整系数;A 为水平向基本地震动峰值加速度。
设计加速度反应谱见图2。 根据桥梁的地震设防烈度、地震动峰值加速度、抗震设防类别、抗震设计方法,得出地震作用参数的数值(表2)。
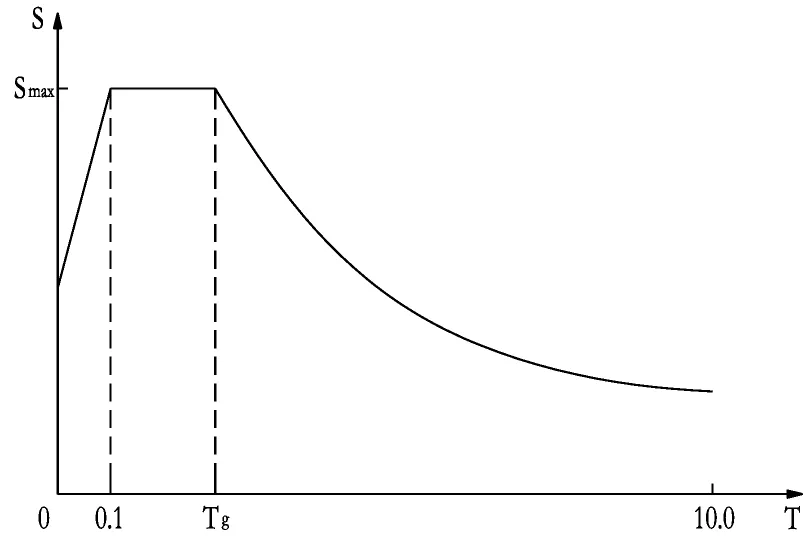
图2 公路桥梁抗震设计加速度反应谱
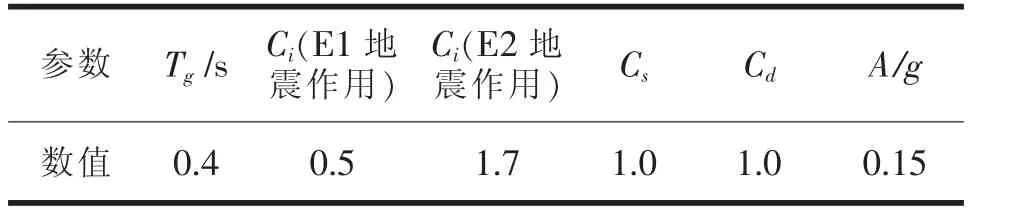
表2 公路桥梁抗震设计参数取值
2.1.2 城市桥梁抗震设计标准
本项目道路等级在城市中定义为城市快速路,依据《城市桥梁抗震设计规范》:水平向设计加速度反应谱S 取值情况如下:
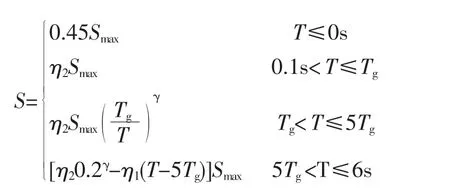
式中:η2为阻尼调整系数 (s);γ 为曲线衰减指数;η1为斜率调整系数(s);其余参数同《公路桥梁抗震设计规范》。
其中反应谱最大值Smax=2.25A (其中的A 值应考虑调整系数Ci)。
设计加速度反应谱见图3。 根据桥梁的地震基本烈度、地震动峰值加速度、抗震设防类别、抗震设计方法,得出地震作用参数的数值(表3)。

图3 城市桥梁抗震设计加速度反应谱

表3 城市桥梁抗震设计参数取值
2.2 抗震性能设计参数对比
从上文公路与城市规范关于地震作用的规定可以看出, 设计加速度反应谱S 值主要有以下不同:(1)反应谱最大值Smax取值不同;(2)周期T 的范围不同[4],如《公路桥梁抗震设计规范》中T 的范围为0≤T≤10 s,而《城市桥梁抗震设计规范》中的范围为0≤T≤6 s;(3)加速度反应谱谱值S 在周期值大于特征周期Tg后的变化曲线不同;(4)E2 地震作用的地震重现期不同,如《公路桥梁抗震设计规范》中的重现期是2 000 年,《城市桥梁抗震设计规范》中重现期是2 000~2 450 年。
以地震作用关联性最大的Smax为例, 根据各自规定计算得出的结果见表4,从表中可以看出,采用《城市桥梁抗震设计规范》 计算得出的E1、E2 地震作用分别比《公路桥梁抗震设计规范》的计算结果大9.6%与8.5%, 因此对于按一级公路兼城市快速路技术标准设计的桥梁,地震作用需要按《城市桥梁抗震设计规范》的规定采用。

表4 抗震性能设计参数对比
3 抗震设计对比结果与分析
3.1 建立模型
在公路桥梁与城市桥梁地震作用对比的基础上,建立了35 m 标准跨桥梁的有限元模型,对抗震分析做进一步的对比。 根据场地的地质情况,为提高模拟的精度,采用土弹簧模拟了实际桩长,同时为准确得出过渡墩的内力情况, 建立了两联的模型[5],即模拟的桥长为2×(4×35)m,整体有限元模型见图4。

图4 标准跨径抗震有限元模型
3.2 抗震设计结果分析
3.2.1 抗震动力特性分析
本桥运用MIDAS/Civil 程序进行动力特性分析,全桥共提取50 阶模态,X、Y 水平向的参与质量分别达到了98.6%与98.4%,前10 阶主要模态的频率与周期结果及振型图分别见表5、图5。
图5 主桥第1 阶振型图(主梁纵飘)
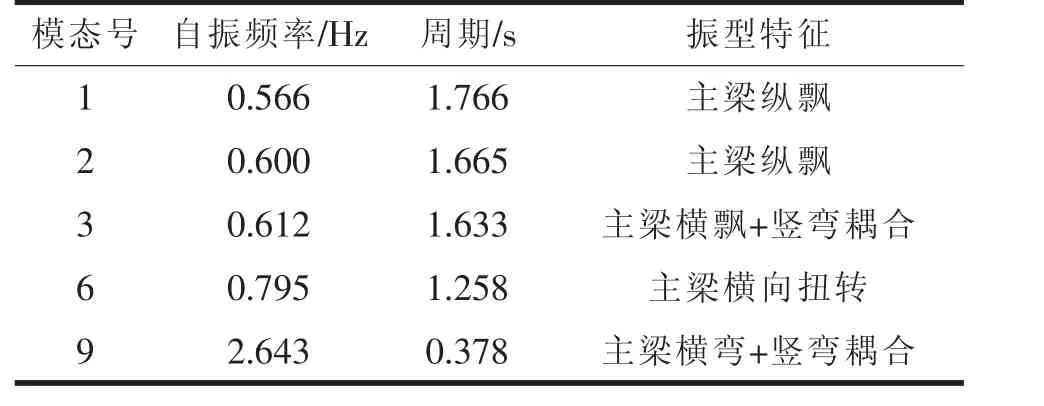
表5 主桥自振频率及振型特征
3.2.2 抗震性能参数分析
桥梁的抗震分析,主要采用能力保护设计方法对桥梁下部结构的强度与变形进行验算,其中桥墩塑性铰区的抗剪验算是重点。 对于采用双柱式桥墩的常规桥梁,纵桥向的桥墩塑性铰区通常发生在墩底, 横桥向的桥墩塑性铰区通常发生在墩顶与墩底。 地震剪力设计值需要根据截面极限弯矩Mu来确定,在计算截面极限弯矩Mu之前,应先判断桥墩是否进入塑性状态, 而判断的依据是等效曲服弯矩My,弯矩-曲率曲线见图6。

图6 弯矩-曲率曲线
3.3 抗震设计验算分析对比
根据两种规范分别计算纵、横桥向桥墩的地震弯矩,并进行对比分析。 为方便比较,本试验假定桥墩支座均满足抗震要求,桥墩的最不利轴力仅考虑恒载作用。 在此基础上,将计算的地震弯矩与纵、横向的等效曲服弯矩My进行比较,判断桥墩在两水准地震工况下,是否进入塑性状态。
3.3.1 公路桥梁抗震设计验算
对建立的有限元模型,依据《公路桥梁抗震设计规范》的要求进行抗震验算,其中的振型组合采用CQC 法,即考虑了振型的相关性,X、Y 两水平向地震荷载采用SRSS 法进行组合。 在E1、E2 地震作用下, 桥墩可能出现塑性铰区位置的最大弯矩、等效屈服弯矩、极限弯矩结果见图7、表6、7。 从表6可知,在E1 地震作用下,桥墩主要位置的能力需求比均大于1,说明桥墩处于弹性状态;从表7 可知,在E2 地震作用下,除过渡墩墩底外,桥墩其他位置能力需求比均大于1,处于弹性状态,而只有过渡墩墩底在顺桥向与横桥向的能力需求比小于1, 即出现了塑性铰,进入塑性状态,因此在这个位置需进一步验算桥墩的剪切强度与变形。

表7 E2 地震作用下桥墩抗弯强度验算结果

图7 E2 地震作用下桥墩纵向最大弯矩图
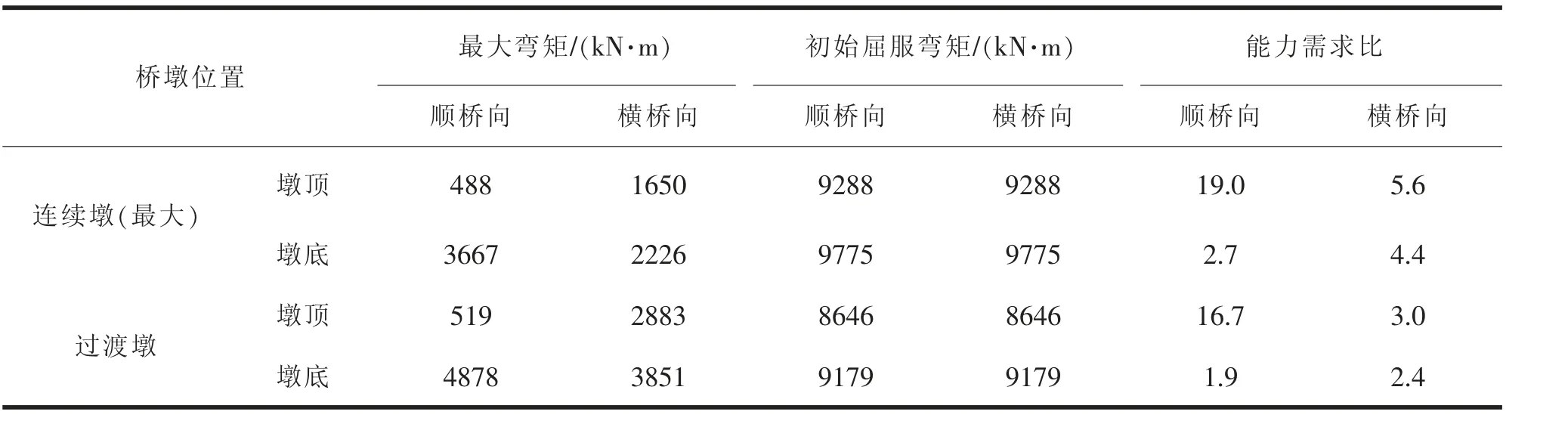
表6 E1 地震作用下桥墩抗弯强度验算结果
3.3.2 城市桥梁抗震设计验算
对建立的有限元模型,依据《城市桥梁抗震设计规范》的要求进行抗震验算,在E1、E2 地震作用下,桥墩可能出现塑性铰区位置的最大弯矩、等效屈服弯矩、极限弯矩结果见图8、表8、9。 从表8可知,在E1 地震作用下,桥墩主要位置的能力需求比均大于1,说明桥墩处于弹性状态;从表9 可知,在E2 地震作用下,连续墩与过渡墩墩底在顺桥向,过渡墩墩顶与墩底在横桥向的能力需求比均小于1,说明在这些位置出现了塑性铰,进入塑性状态。 同上,在这些位置需进一步验算桥墩的剪切强度与变形。

图8 E2 地震作用下桥墩纵向最大弯矩图

表8 E1 地震作用下桥墩抗弯强度验算结果
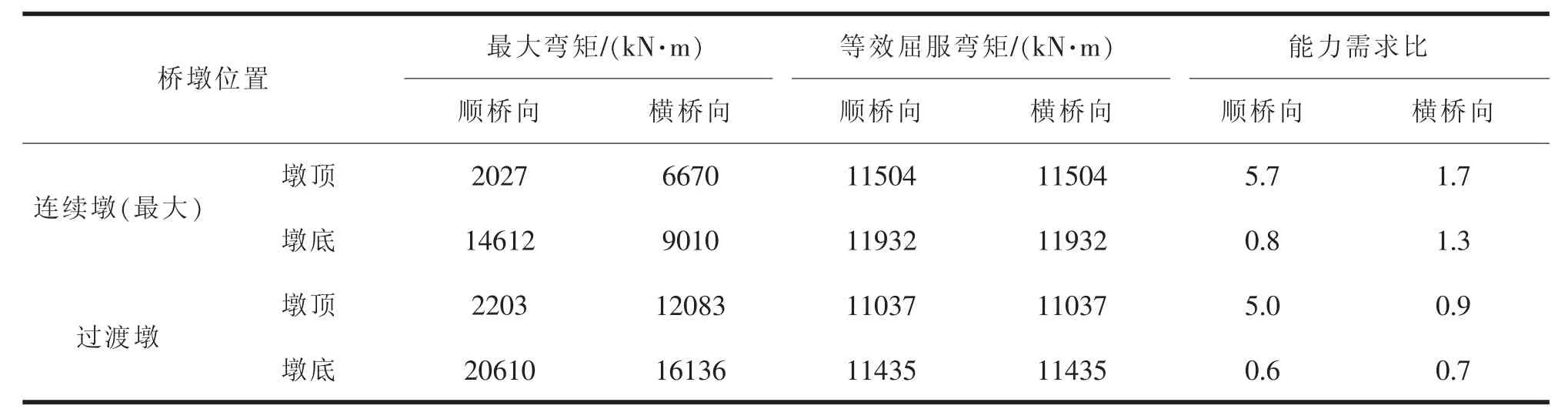
表9 E2 地震作用下桥墩抗弯强度验算结果
3.3.3 抗震设计对比分析
依据两种抗震规范计算E2 地震作用下的最大弯矩结果见表10。从表10 可知,桥墩不同位置采用《城市桥梁抗震设计规范》 计算得出的最大弯矩值比《公路桥梁抗震设计规范》 的计算结果大19%~25%,因此依据《城市桥梁抗震设计规范》的计算结果更不利。
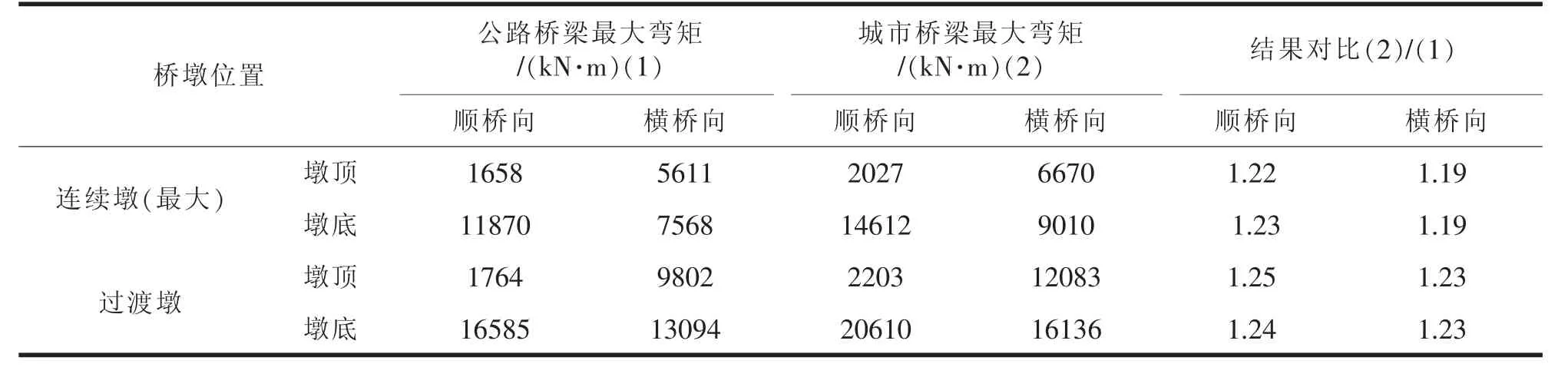
表10 E2 地震作用下的最大弯矩对比
4 结论
(1)对于一级公路兼城市快速路的桥梁,在抗震设计时,E1、E2 地震作用的取值,《城市桥梁抗震设计规范》 分别比 《公路桥梁抗震设计规范》大9.6%与8.5%,因此设计时,地震作用需要按《城市桥梁抗震设计规范》的规定取值。
(2)进行抗震分析时,在E2 地震作用下,桥墩不同位置依据《城市桥梁抗震设计规范》计算得出的最大弯矩值比《公路桥梁抗震设计规范》的计算结果大19%~25%, 因此在大桥振型周期较短的情况下,计算结果即出现了较大的差异。 而对于具有长周期的大跨度桥梁,地震作用效应的差异将更加明显。
(3)按照本桥下部结构拟定的尺寸,依据公路桥梁或城市桥梁抗震规范计算在E2 地震作用下的结果可知,桥墩均出现了塑性铰的情况,说明采用常规支座,无法保证地震工况下桥墩处于弹性工作状态,因此需要采取减隔震措施(如设置减隔震支座),以减轻地震作用的影响。
