浮盘式自适应流入控制装置控水性能及结构参数优化
2021-11-12薛世峰雷玉建朱秀星王海静
贾 朋, 薛世峰, 雷玉建, 朱秀星, 周 博, 王海静, 朱 渊, 房 军
(1.中国石油大学(华东)储运与建筑工程学院,山东青岛 266580; 2.石油工程教育部重点实验室(中国石油大学(北京)),北京 102249)
水平井已经被广泛应用于油气开采中。但是由于储层非均质与各向异性[1-2]、天然裂缝[3]以及跟趾效应[4]等因素导致长水平井入流剖面不均衡,过早发生水/气侵入,严重影响了油井产量。为了抑制这种不均衡现象,延缓含水率上升速度,常利用入流控制装置(ICD)限制水/气流入,均衡生产段入流剖面[5-7]。根据流体通道的面积或长度能否随流体性质自动调节,ICD可分为被动式(PICD)和主动式(AICD)两种[8]。AICD由于其自适应调节的优点得到深入研究,相继出现了多种结构形式,主要有浮力型、流道型、遇水膨胀型、浮盘型以及先导控制型等。其中浮力型AICD利用浮阀所受浮力工作[9],可有效地抑制气体突破。流道型AICD利用流体惯性力与黏性力的比例关系改变流体流动路径[10-11],将较高雷诺数流体引入涡流室[12-13]增加其流道长度,产生较大阻力,遏制其产出;将较低雷诺数流体引入捷径流出,提高其产量[14-16]。遇水膨胀型AICD利用遇水膨胀橡胶作为节流元件,在水侵发生后膨胀减小通流面积,抑制水的产出[17-18]。浮盘型AICD是由Stateoil公司开发的一种依据流体性质、流动条件自动调整流通面积的AICD,可有效地减少低黏流体的流入[19-20]。先导控制型AICD也称AICV,是在浮盘型AICD基础上增加了先导层流流道控制浮盘开关[21-22]。这些AICD的工作原理不同,具有不同的适用条件,笔者主要研究浮盘式AICD的工作特性。目前关于浮盘式AICD的研究主要集中于工程应用[23-24],利用试验得到的流量-压力关系曲线进行控水采油效果分析,而关于浮盘式AICD本身工作性能的研究则主要是通过试验或CFD模拟的方式进行[25-26],很少有关于结构参数对其工作性能影响的理论研究。为此笔者以浮盘式AICD为研究对象,采用理论分析与数值模拟相结合的方法,建立其稳态力学模型,然后从其内部流动特性出发,分别讨论结构参数、流体性质、入口流速对其工作特性的影响。
1 工作原理与力学模型
1.1 工作原理
如图1所示,浮盘式AICD由可以自由浮动的盘式阀芯和固定的上、下阀座组成。它通过作用在阀盘表面上的压力平衡来工作。该压力由涉及动能、压能、势能以及摩擦损失的伯努利方程决定。不同黏度的流体流经浮盘式AICD时,阀盘表面上的压力典型分布如图2所示。对于低黏度流体,摩擦损失较小,阀盘上表面的压力分布主要由加速压降决定,分布如图2右侧曲线所示,将盘面上的压力积分可得到向上的轴向力,使阀盘向上运动,开度减小;对于高黏度流体,摩擦损失较大,阀盘上表面的压力分布如图2左侧曲线所示,积分得到的轴力向下,使阀盘向下运动,开度增大。因此相同压力下高黏度流体的流量比低黏度流体的流量大。
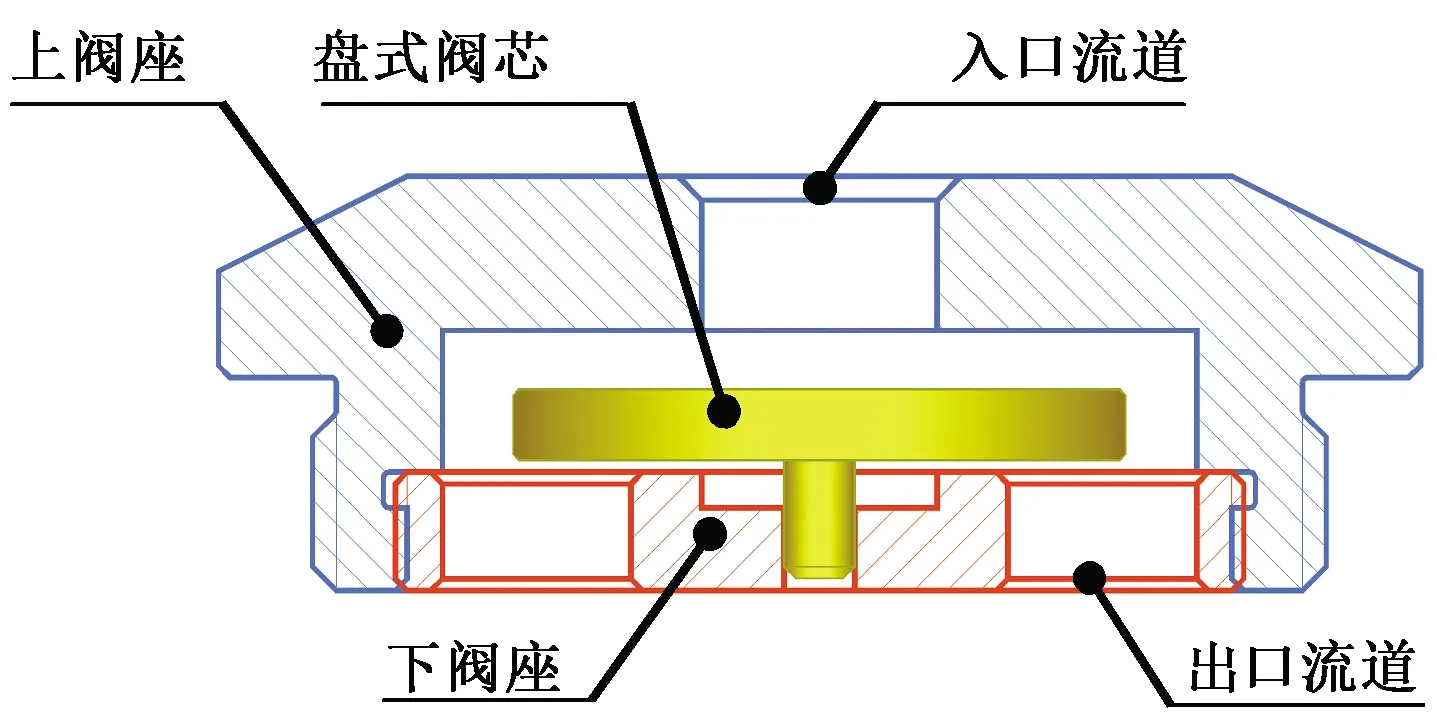
图1 浮盘式AICD结构示意图Fig.1 Schematic diagram of floating disc AICD
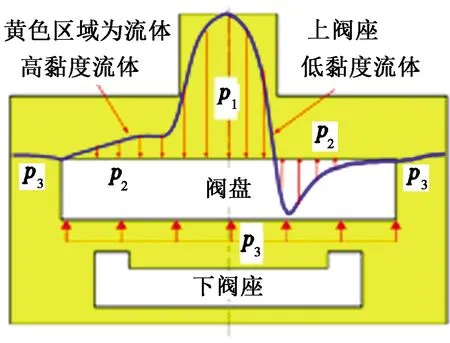
图2 不同黏度流体中盘面上的典型压力分布Fig.2 Typical pressure distributions on surface of disc in fluids with different viscosities
1.2 浮盘式AICD力学模型
阀盘上的压力分布决定作用其上的轴向力分量,轴向力的平衡则控制阀盘的开度,并最终决定流量大小。为了便于建立阀盘受力的数学模型,将阀盘表面分为两部分:一部分是与入口流道相对的未遮盖面积,其上压力分布为p1;另一部分是被上阀座遮盖的面积,压力分布为p2。
轴向力可由阀盘表面上的压力积分求得
(1)
其中
A=A1+A2.
式中,Fa为沿阀盘轴线方向的力,N,在图2中向下为正;A1、A2分别为阀盘上表面未被遮盖和被遮盖部分的面积,m2;A为阀盘总迎流面积,m2;G为阀盘浮重,N;θ为阀盘上表面法线的倾角,与管柱在井下的安装方向有关;Ff为阀盘所受的轴向摩擦力,N;p3为阀盘下表面上的分布压力,Pa。
式(1)表明,轴向力与流道内的压力分布有关,而压力分布又与流道几何尺寸、流体性质和边界条件有关。对于给定的流体性质和边界条件,如何设计几何尺寸是实现浮盘式AICD选择性阻流的关键。
1.3 阀盘表面压力分布
1.3.1 阀盘未遮盖表面压力计算
阀盘未遮盖部分的压力分布p1难以求得,可取图3所示圆柱形控制体(1-1,2-2)为对象,在入口轴向应用动量定理可得该积分式的具体表达式为
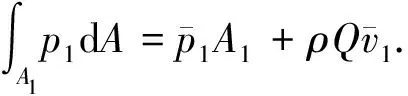
(2)
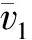
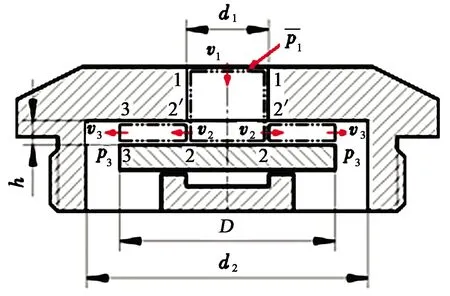
图3 浮盘式AICD计算结构简图Fig.3 Structure diagram of calculation of floating disc AICD

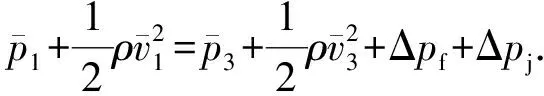
(3)
其中
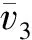
式(3)中忽略了两截面之间的位势差。
1.3.2 阀盘遮盖表面压力分布
阀盘被遮盖表面上的压力分布受入口流动影响,变得十分复杂。将这部分流动简化为阀盘与上阀座之间的圆盘形径向间隙流。在圆柱坐标系下研究该流动,由于阀盘与阀座的缝隙高度h很小,假设缝隙内的流动为轴对称层流,对称轴为z轴,并假设z方向的速度可以忽略,压力在z方向均匀分布。因此圆柱坐标系下,不可压缩黏性流体的定常轴对称流动的连续性方程为
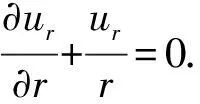
(4)
运动微分方程为
(5)
式中,ur为流速径向分量,m/s,是坐标z和r的函数;μ为流体的动力黏度,Pa·s。
由式(5)可知,缝隙内压力梯度由两部分组成:一部分是由黏性引起的压力变化(右侧第一项);另一部分是由流体加、减速引起的压力变化(右侧第二项)。该微分方程为非线性微分方程,很难给出其精确解。将分别求解这两部分压降,然后将其叠加近似得到总的压力损失。计算中用到的边界条件和连续性条件为

(6)
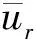
摩擦压降[27]为
(7)
式中,R为阀盘外缘半径,m。
可求得加速压降为
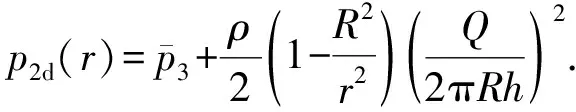
(8)
将式(7)和(8)合并可得阀盘遮盖部分近似的总压力分布为
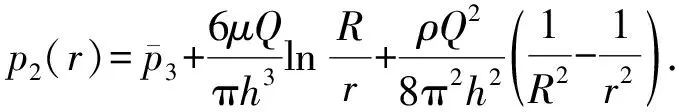
(9)
由式(9)可知,阀盘遮盖部分的压力分布与阀的开度、结构尺寸、入口流量和流体物性有关。将式(9)在阀盘遮盖面积上积分可得与其对应的轴向力分量。
将式(2)、(3)、(9)代入式(1)并积分可得轴向力的最终表达式:
Gcosθ∓Ff.
(10)
式中,ri为入口流道半径,m。
根据式(10)所述的轴向力模型可以分析流动条件、流体物性、结构尺寸对浮盘式AICD工作性能的影响。
2 局部损失系数计算
利用动量定理和伯努利方程求解阀盘未遮盖表面压力时,需用到入口流道拐角处的局部损失系数ζ2。通过数值试验方法确定该系数。
入口拐角处(2-2′截面)的压降与ρ、μ、v及几何尺寸di和h有关。它们之间存在函数关系:
f(Δp,ρ,μ,v,di,h)=0.
(11)
其中

通过量纲分析,可把阻力系数表示成无量纲积的函数:
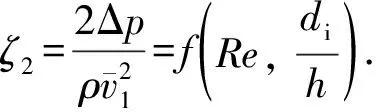
(12)
由于不同位置处雷诺数不同,因此雷诺数的表达式为
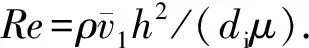
(13)
通过对CFD结果的统计得到局部损失系数的计算公式。CFD数值模拟的设置如下:将浮盘式AICD的结构进行简化建立如图4所示的四边形网格模型,阀盘左右网格细化。根据浮盘式AICD的结构特点采用轴对称模型,入口设为速度边界,出口设为压力边界,壁面为无滑移壁面,采用标准湍流模型以及标准壁面函数。
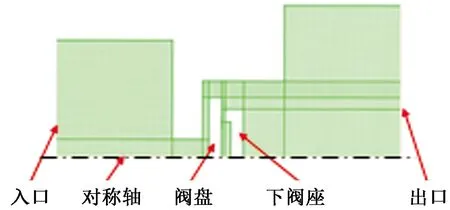
图4 浮盘式AICD的CFD计算模型Fig.4 CFD model of floating disc AICD
改变阀盘开度和浮盘式AICD的结构尺寸,可得一系列的CFD模拟结果,从中提取压力、流速及其他设置参数可得局部损失系数和所定义的Re之间的对应关系,如图5中散点所示。
拟合数值结果,可得计算局部损失系数的公式:
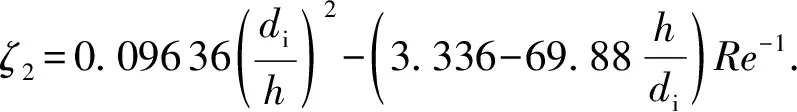
(14)
由图5可知,阻力系数随Re增加而减少,随di/h增大而增大,即di不变时ζ2随阀口开度的减小而增大。由图5还可以得出,当Re>10,阻力系数近似保持常数,因此将Re=10作为本问题的临界值。
将式(13)代入式(14)可知,当di/h趋于0,即开度足够大时,局部阻力系数趋于零;当di/h趋于无穷大,即开度无限小时,局部阻力系数趋于无限大。当Re>10且阀盘开度h>0.72di时,阻力系数降到0.05以下。因此可以取0.72di作为阀盘最大开度的设计依据,该值比以通流面积相同为依据得到的开度约大3倍。

图5 局部损失系数数值模拟结果与拟合公式结果对比Fig.5 Comparison between results of numerical simulation and results of fitting formula
确定局部损失系数的经验表达式之后,可将式(14)代入式(10),可由流动条件、流体物性、结构尺寸完全确定轴向力。
3 阀盘压力分布计算结果
阀盘遮盖部分压力分布的数值结果和模型结果随雷诺数的变化规律如图6所示。

图6 不同雷诺数下遮盖部分压力沿径向分布Fig.6 Pressure distribution along radial direction under different Reynolds numbers
由图6可知,当雷诺数较小时,内部流动为层流,图3中2-2′拐弯处没有形成涡流或涡流范围很小,因此遮盖部分压力分布的数值结果与模型结果吻合很好;随着雷诺数增加,拐弯处会出现较大范围的涡流,使遮盖部分入口起始段的速度沿径向先增大再减小,从而出现图6(b)所示的压力沿径向先减小后增大的现象。所建立的模型无法描述拐弯处(入口段)速度变化的影响,因此模型结果与数值结果在入口段相差很大,但在离入口段较远处两者吻合较好。
由图7可知,虽然数值方法与模型方法的压力分布曲线相差较大,但积分后的轴向力差值并不大。由图7可知,遮盖部分轴向力随雷诺数增大先增大后减小;当雷诺数大于50后,遮盖部分轴向力随开度增大而减小。由于本文中规定轴向力向下为正,所以当雷诺数大于50后,遮盖部分轴向力使阀盘向上运动,阀口有关小的趋势;当雷诺数较小,即黏性力起主导作用时,阀盘是向下运动的。

图7 不同开度下遮盖部分轴向力随雷诺数变化曲线Fig.7 Variation curve of axial force of covering part with Reynolds number under different openings
4 压力-流量关系影响因素
浮盘式AICD的压力与流量关系中的压力是其入口与出口的压差,可在式(3)的基础上,加上图3中1-1截面突缩引起的压力损失求得:
(15)
式中,ζ1为1-1截面突缩处的局部阻力系数,其计算公式可参考文献[27]。
利用式(10)、(13)、(14)和(15)分析浮盘式AICD的压力-流量关系,具体步骤如下:
(1)首先给定浮盘式AICD的结构尺寸R和ri,流体物性ρ和μ,浮重G和安装方位θ。
(2)给定一个流量Q,并令总轴力Fa=0,可以解出一个开度h。
(3)将开度h和流量Q代入式(15),可得流体流经浮盘式AICD的压差。
(4)改变流量Q,重复步骤(2)~(3)可得压力-流量曲线。
4.1 与试验结果对比
图8给出了应用新模型计算得到的压力-流量关系曲线,与文献[28]试验结果进行对比。由于无法得到试验所用浮盘式AICD的结构参数,因此首先调整结构参数ri、R和hmax,使模型结果与油的试验结果达到较好的匹配;然后再使用根据油的试验结果标定的结构参数来计算纯水的模型结果。由图8可知,纯水和油的计算结果均与试验结果吻合较好。
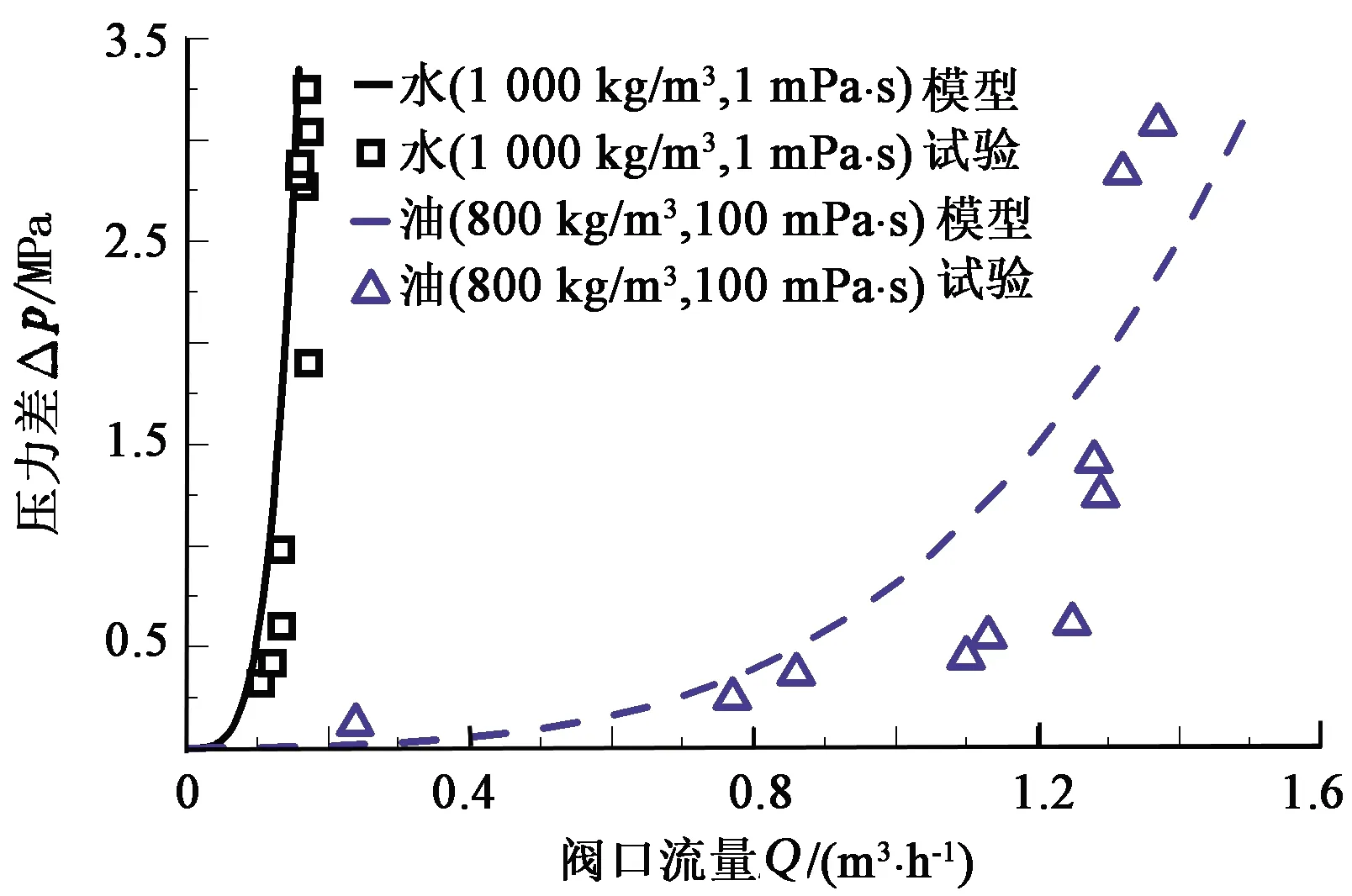
图8 压力-流量关系模型结果与试验结果对比Fig.8 Comparison of theoretical and experimental results of pressure-flow relationship
4.2 流体物性对压力-流量关系影响
浮盘式AICD根据流体物性进行选择性阻流,因此首先分析流体物性对压力-流量关系的影响。图9给出了密度为900 kg/m3时,不同流量下黏度对AICD压差和阀盘开度的影响。由图9(a)可知,不同流量下压差随黏度的变化趋势不同。当雷诺数较小时,阀盘坐在下阀座上始终处于最大开度处(图9(b)所示),阀盘与上阀座缝隙中的压降主要由流体黏性引起的,因此压差随黏度增加而线性增加。流量增大到0.049 8 m3/h后,当黏度较小时,加速压降占主导地位,阀盘在向上轴向力作用下离开下阀座一定距离,该距离随黏度增加而减小,因此压差减小;当黏度增大到一定程度后,阀盘完全坐在下阀座上保持最大开度不变,此时黏性压降起主要作用,因此压差又随着黏度增大而增大。当流量增大到一定程度后,加速压降始终处于主导地位,黏性压降随着黏度增加而增大导致阀盘开度增大,因此压差随黏度增大而减小。

图9 黏度对压差和阀盘开度影响Fig.9 Influence of viscosity on pressure difference and valve disc opening
图10给出了黏度为10 mPa·s时,不同流量下密度对AICD压差的影响。当流量很小时,压差随密度增大而线性减小。这是由两个原因引起的:流量很小时,负值加速压降很小不足以使阀盘升起,阀盘开度保持最大值不变;阀盘开度最大时局部阻力损失系数远小于1,因此由式(15)可知,压差随密度增大而线性减小。当流量增大到一定程度后,雷诺数也增大,阀盘升起,其开度随密度、黏度等因素而变化。因此压差不再与密度呈简单的线性关系,而是随着密度增大而非线性增大。
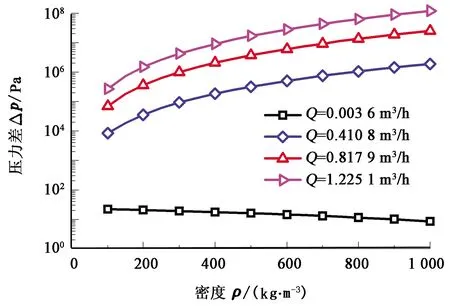
图10 密度对压差影响Fig.10 Influence of density on pressure difference
4.3 结构参数对压力-流量关系影响
图11给出了不同流量下在标准水和油(900 kg/m3,30 mPa·s)两种介质中,ri对压差的影响。图11中所使用的R=7.5 mm。由图11可知,不同流量下压差都随ri增加而降低。流量很小时,相同流量下水的压差比油的压差下降的快。流量达到一定程度后,在ri=2.25 mm附近水的压差变化趋势出现拐点。这是因为:当ri<2.25 mm时,阀盘几乎完全关闭,产生很大的压差;当ri>2.25 mm后阀盘开度逐渐增大,在入口流道节流和阀盘-上阀座间缝隙节流共同作用下压差变化趋于平缓。相比而言,油的压差随ri增大一直比较平缓。对于较大的流量,当ri<2.25 mm时油的压差显著小于水的压差;当ri>2.25 mm后,油与水压差相差不大,但仍小于水的压差。所以当R=7.5 mm,ri<2.25 mm时AICD具有很好的稳油控水效果。

图11 ri对压差影响Fig.11 Influence of ri on pressure difference
图12给出了ri为1.5 mm时不同流量下在标准水和油两种介质中,不同R对压差的影响。由图12可知,当流量很小时,水的压差随R增加而减小,油的压差随R增加而增大。这是因为:当流量很小时,油介质中阀盘处于最大开度不变,所以压差随缝隙流道长度R的增加而增加;在水介质中,黏性压降小于加速压降使阀盘处于某一开度,此时增加R将导致黏性压降增加使阀盘开度增加,因此压差随开度的增加而降低。当流量很大时,对于油和水来说,压差都是随着R增加先增加后减小;相同流量下,油与水的压差在R较小时相差不大,但随着R增大而增大。由图12还可知,水的压差随着R增加先增大后减小,转折点处的R可以看作ri=1.5 mm时的最优值,因为此时AICD的阻水效果最好。而且相同ri下,转折点处的R随流量的变化而变化很小。基于此,图13给出了流量为0.678 6 m3/h时,不同ri下压差随R变化曲线。由图13可知,转折点的R随ri增大而增大,例如,当ri=1.25 mm,R≈7.25 mm或ri=2.15 mm,R≈11 mm时可达到最优控水效果。
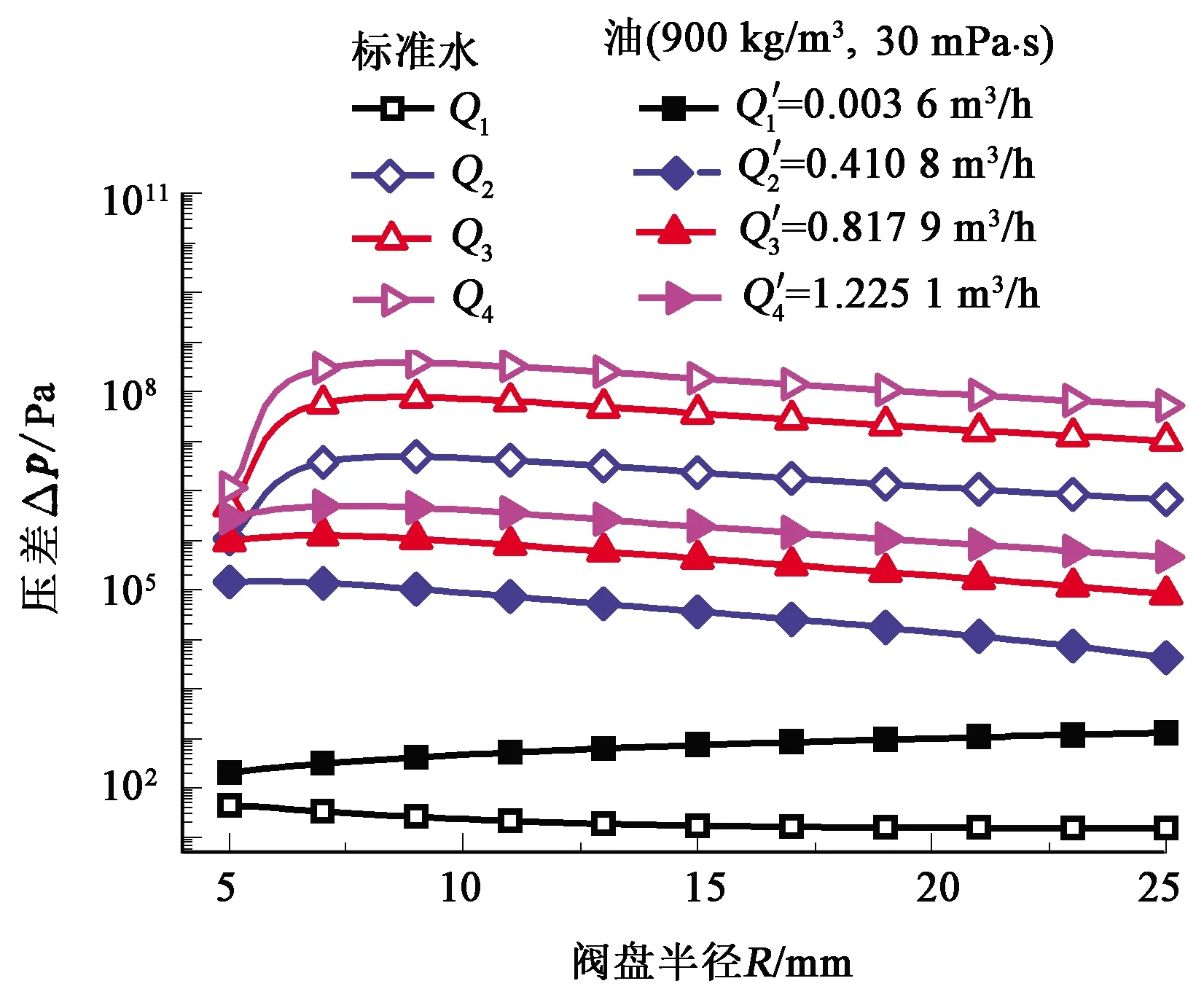
图12 不同流量下R对压差影响Fig.12 Influence of R on pressure difference for different flow
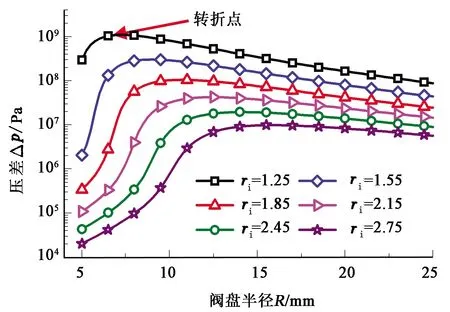
图13 不同ri下R对压差影响Fig.13 Influence of R on pressure difference under different ri
5 结 论
(1)阀盘遮盖部分入口处的阻力损失系数与结构参数di/h的平方和雷诺数的倒数呈线性关系,随di/h增加而增加,随雷诺数增大而减小。
(2)油井常规产液量下水介质在浮盘式AICD中的压降随入口流道半径的变化曲线存在拐点。当入口流道半径小于拐点对应值时得到较好的稳油控水效果;当入流流道半径大于拐点值时油、水的压降趋于相同,稳油控水效果不明显。
(3)对于给定的流量和入口流道半径,水介质的压降随阀盘半径的变化曲线存在转折点,转折点处水相压差最大,不同入口流道半径下转折点对应的阀盘半径可作为浮盘式AICD结构参数的优选值。
