电驱动系统可靠性目标载荷快速构建方法研究
2021-11-12邓思城赵礼辉郑松林
邓思城 ,赵礼辉 ,2,3,王 震 ,周 驰 ,郑松林 ,2,3
(1.上海理工大学 机械工程学院,上海 200093;2.机械工业汽车机械零部件强度与可靠性评价重点实验室,上海 200093;3.上海新能源汽车可靠性评价公共技术平台,上海 201108)
可靠性是新能源汽车的重要技术指标,也是当前影响其用户认可度的主要因素。电驱动系统作为新能源汽车的主要动力源(纯电动、增程式、燃料电池的唯一动力源),其可靠性是整车可靠性的重要构成部分,直接关系到整车的运行安全[1]。在汽车研发体系中,基于车辆服役载荷的可靠性设计、分析和试验是保障其在用户使用条件下可靠性水平的重要方式,其中能够复现不同用户车辆行驶过程中性能退化的工况载荷则是开展这些工作的前提。
由于驾驶行为、载重状态、路面起伏、交通状况各不相同,电驱动系统在不同用户使用条件下载荷差异巨大,为保证用户使用过程中车辆的可靠性,试验载荷需要覆盖足够的用户百分位水平(如95%),即目标载荷。可靠性目标载荷的构建,需要以大量用户样本数据为基础。直接通过用户车辆进行载荷采集的方式成本高、周期长,用户样本量往往较低[2];仿真方法成本低、载荷获取快速,是车辆载荷获取的重要方式。然而,行驶路况与外部环境的随机性[3],使仿真结果与实际用户载荷偏离较大,进而影响整体损伤水平的确定。
多年来,国内外研究人员围绕车辆运行数据(含载荷数据)和运行状态间的相互关系开展了大量研究,取得了丰硕的成果。张抗抗[3]等研究了电动车行驶阻力的贡献量,确定车辆运行过程中行驶阻力随着坡度的增加基本呈正比增加。夏光等[4]指出道路坡度与整车质量为影响车辆行驶阻力的主要参数,而风阻与滚动阻力系数基本固定,在速度较低时的影响可以忽略不计。FATHY等[5]以实测车辆运行数据为基础,结合整车质量上下限收敛,采用递归最小二乘法,得到行驶过程中车辆质量的有效估计。RAJAMANI等[6]和KIM等[7]基于实采悬架加速度和位移数据,采用平均法对整车动力学模型中的质量参数进行了估算。VAHIDI等[8-10]提出了一种平均估算法,基于车速、纵向加速度等信息实现了车辆质量、行驶阻力和道路坡度估计。雷雨龙等[11]通过纵向动力学模型,基于扩展卡尔曼滤波方法实现了车辆质量及道路坡度估计。诸文博等[12]通过提取驱动力信号和纵向加速度信号的高频部分,使用递归最小二乘法进行车辆质量与道路坡度估算。郝胜强等[13]通过稳态卡尔曼滤波法估算整车质量与道路坡度。综上研究可知,目前研究多聚焦于通过车速、驱动力、纵向加速度等运行数据估计车辆行驶道路坡度与整车质量等运行状态,较少开展反向研究。文献[3]和文献[4]虽然给出了与驱动力相关的影响因素,但并未进一步形成有效估计方法。在电驱动系统可靠性载荷构建过程中,不同用户使用条件下的车速信息相对容易获取,但转矩、转速等载荷信息往往缺失。鉴于坡道、质量等因素对驱动系统载荷的强相关性,如何考虑这些因素的影响,并通过已有车速数据构建有效的电驱动系统可靠性目标载荷,尚缺乏有效方法。
为此,本文提出一种基于不同用户车辆历史车速数据的电驱动系统可靠性目标载荷构建方法。以整车动力学仿真模型为基础,通过等效质量和等效坡度的参数优化,实现用户长期使用过程中仿真载荷与实际载荷损伤及频次分布的一致。进一步结合全体用户损伤累积分布,通过百分位损伤水平下参数统一,构建覆盖一定用户使用强度的电驱系统可靠性目标载荷,从而为快速准确地进行电驱动系统可靠性评估与寿命预测奠定基础。
1 整车及电驱动系统动力学建模
1.1 整车参数
本文研究的车辆为某品牌的新能源汽车,其基本参数见表1。

表1 整车基本参数
1.2 整车及电驱动系统数学模型
根据整车在行驶过程中的阻力与驱动力关系,可知整车受力平衡方程[14-15]:

式中:Ttq为电机轴转矩,Nm;i、η分别为总传动比和传动效率,组成减速器模型;r为轮胎半径,m;m1为整车等效质量,kg;f为轮胎滚动阻力系数,取值为[16]为空气阻力系数;A为迎风面积,m2;α为等效坡度,%,组成车身模型;v为车速,m/s;a为汽车加速度,m/s2。
根据减速器模型,得到的电机转速,结合转矩可由式(2)[17]计算电机功率:

式中:n为电机转速,r/min。
本研究着重考量电驱动系统载荷,不涉及功率损失,将汽车行驶过程中电机驱动功率近似等于电池输出功率,忽略辅助功率器件的影响,可得:

式中:Ubat、Ibat分别为电池输出电压和电流;Umot、Imot分别为电机输入电压和电流。
由此可以求得电池电压、电流变化与剩余SOC,从而构成电池模型。制动模块根据前后车轮抱死情况进行分析[18-19],得到制动控制模块。整车模型以式(1)为基础,连接数学模型,建立整车动力学仿真模型,如图1所示。

图1 电动汽车整车动力学仿真模型
1.3 仿真参数影响
1.3.1 等效参数分析
以40位用户车辆历史服役时长为2年的数据为基础,又以车速数据和电机轴转矩数据为对象进行研究,使用第1年数据进行分析,第2年数据对比验证。鉴于整体数据量较大,从中选取10位用户进行不同参数设置下仿真载荷单位里程损伤强度对比分析,10位用户的行驶时间和里程如图2所示。

图2 行驶时间和里程
车辆行驶过程中的道路坡度α、车辆载质量mv对整车动力学仿真结果具有重要影响,而同一等效参数的仿真结果对不同用户优劣各异。为对比等效参数的变化对仿真转矩造成的损伤变化和时域分布的影响,以及各用户仿真损伤精度的差异性,以3种状态进行载荷仿真(表2),并与实际载荷进行比较分析。

表2 整车载荷仿真状态参数
基于仿真载荷数据,结合S-N曲线和Miner线性损伤累积理论[20-21],各用户单位里程损伤结果如图3所示。参数为状态1时,10位用户都未达到预期损伤水平,在状态2和状态3时,部分用户损伤有较高精度,前者对损伤的提升最高可达50%,后者最高可达30%。各状态参数下用户仿真损伤与实际损伤进行分布拟合,服从对数正太分布,累积概率分布如图4所示,不同状态参数下95%损伤覆盖水平皆未达到实际效果,状态1参数下相差最大。

图3 用户不同参数仿真损伤

图4 损伤累计概率分布
以图2中5号用户为例进行时域分布对比。对变程分布和幅值分布进行归一化处理,结果如图5和图6所示。状态1参数下的仿真载荷在两种分布下与实际偏离最大,参数为状态2时偏离最小,仿真最大变程为实际的0.92倍,正向幅值大小都符合实际水平。

图5 变程分布

图6 幅值分布
通过对比分析可知,行驶坡度与载质量对转矩损伤强度和时域分布都有较大的影响,且不同用户难以基于同一参数仿真得到高精度载荷数据。
1.3.2 用户不同时段损伤一致性分析
对于每个用户,其驾驶行为相对固定,行驶路线及载质量状态具有高频分布特征,所以同一用户不同时间段驾驶工况的剧烈程度存在一定的关联性。通过模型仿真,研究200组随机参数状态下用户群体第1年与第2年数据仿真载荷95%损伤水平下相对实际的误差,如图7所示。两者误差差值绝对值对比如图8所示,最大值为14%左右,大部分处于10%以下;其大小随着两者误差的减小而减小,当误差小于10%时较小,为1%左右。两者误差的Pearson相关性为0.996,相关性极强。因此,对于该用户群体,仿真载荷损伤百分位水平越接近实际,后续构建的目标载荷可靠性覆盖度更准确。

图7 95%损伤水平误差对比
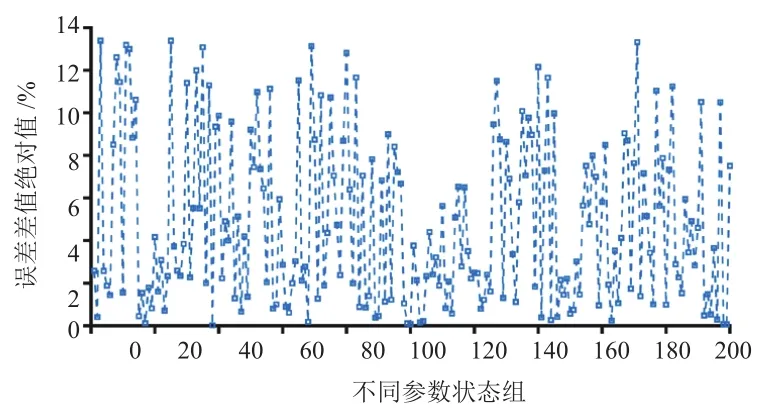
图8 误差差值绝对值对比
2 损伤与等效参数的函数拟合
为建立以损伤强度为目标的优化数学模型,构建电机轴损伤强度随行驶坡度d和整车质量m变化的函数关系式。
由表1可知,车辆最大载质量为500 kg;上坡路段对车辆转矩的影响要远大于下坡[22],且大部分道路坡度要小于12%。将1 500 ~2 000 kg整车质量等间隔100 kg、坡度0~12%等间隔1%进行仿真,以图2中1号用户为例,各等级参数下仿真转矩单位损伤强度见表3,损伤分布如图9所示。随着二者参数的单独增加,损伤均呈线性增加。
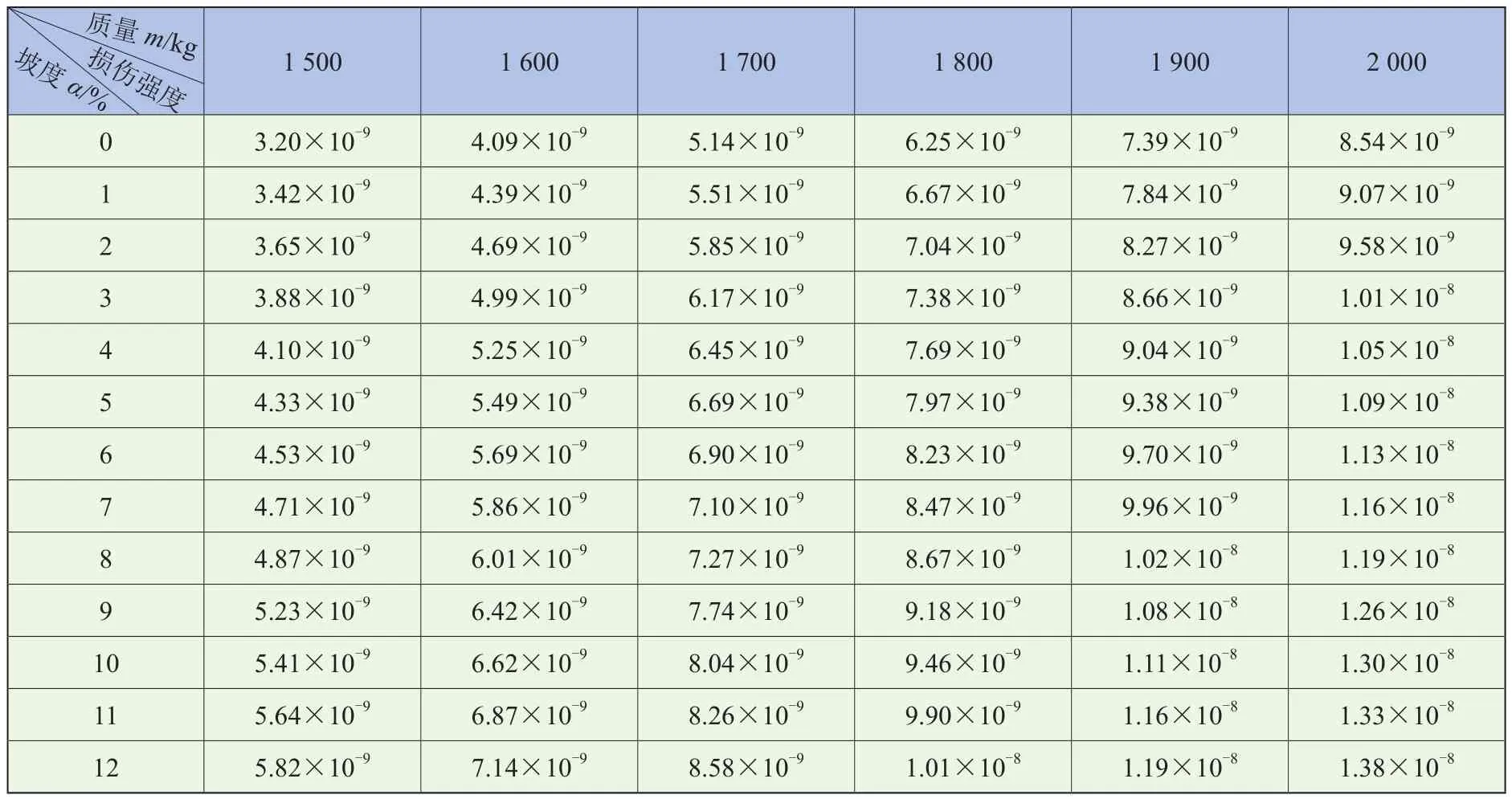
表3 各等级参数下单位损伤

图9 各等级参数损伤分布
根据表2数据,拟合出1号用户单位损伤强度关于整车等效质量、行驶坡度的近似函数关系式为:

考虑车辆实际状态,整车等效质量及坡度取值区间如下:1 500 kg≤m1≤2 000 kg,0≤α≤12 %。使用拟合的函数关系式,对各等效质量和坡度进行损伤计算,拟合误差如图10所示,最大为3%左右。

图10 各等级损伤误差
3 单个用户参数优化
3.1 参数优化模型
3.1.1 损伤强度优化目标函数构建
将实际损伤与拟合损伤的函数关系做差的绝对值,定义为转矩损伤的优化目标函数:

式中:f1j、dj、dacj分别为第j位用户的损伤目标函数、损伤数学模型和实际损伤值。
3.1.2 时域分布优化目标函数构建
考虑仿真转矩时域分布效果,根据式(1)对任意时刻仿真与实际转矩做差的绝对值作为目标函数时,会引入大量方程,得到复杂解。将各时刻转矩差值求和,能有效减少计算量、得到统一解。由于制动时受到制动策略控制,不完全符合式(1)。将仿真与实际驱动正转矩各时刻的差值绝对值求和,根据式(1)得:
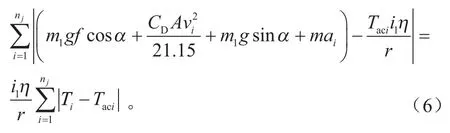
式中:nj为第j位用户驱动转矩出现的总次数;Ti、Taci为第i次出现的仿真和实际驱动转矩。
由表3可知坡度取值小,则可令:

根据三角不等式可得:

根据式(7)和式(8),第j位用户的转矩时域分布优化目标函数定义为:

将采集的历史服役数据计算求和,可得式(9)各项系数。
3.1.3 变量及约束条件
以道路坡度和整车等效质量作为变量,以两者正常取值区间作为约束条件,具体为:
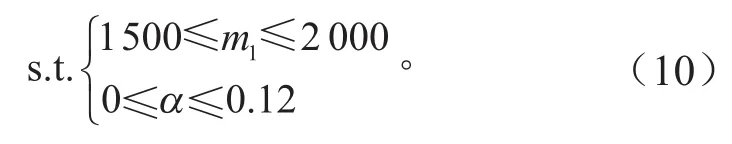
3.1.4 优化模型
根据式(5)~(10),可将第i位用户的仿真转矩多目标优化问题进行如下描述:

3.2 优化结果分析
结合优化模型为典型的多变量、多目标优化模型,采用非支配排序遗传算法-II(Non-Dominated Sorted Genetic Algorithm-II,NSGA-II)对不同用户进行参数优化求解[23]。各用户参数经200次迭代,可得到等效坡度和等效质量Pareto最优解。选取的10位随机用户对应的最优解见表4,其中用户5的坡度解最大,用户7的整车质量解最大,而9号用户坡度和质量解都处于较高水平,单位损伤强度高。基于优化参数进行仿真,与实际损伤最大误差为4.08%。群体用户仿真与实际损伤服从对数正太分布模型,累计概率分布如图11所示,两者95%期望损伤水平基本一致。

图11 损伤累积概率

表4 实际与仿真转矩单位损伤对比表
以损伤相对误差最大的用户(5号)为例进行说明,两个时间段内的转矩相对变化如图12所示,转矩归一化处理后,优化参数仿真载荷极值与实际载荷极值吻合度更高。变程与幅值分布如图13和图14所示,参数优化后仿真载荷幅值分布更为贴近实际,在幅值较大时明显,且正向振幅频次显著提高,近似实际分布。

图12 转矩时间历程片段
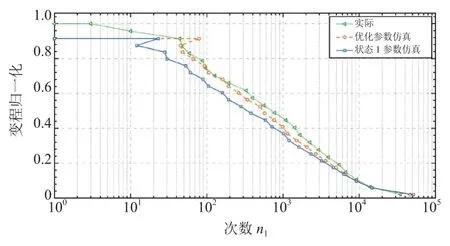
图13 变程分布

图14 幅值分布
4 群体用户参数统一
4.1 参数统一的优化模型构建
对Y~N(0,1),可知:

由图4和图11可知,仿真与实际用户损伤服从对数正态分布。根据式(12),以群体用户仿真和实际转矩损伤取对数的平均值、标准差和对应95百分位损伤作差的绝对值定义为目标函数:

根据式(9),将各用户转矩时域分布优化目标函数求和获得以群体时域分布作为目标函数:

变量和约束与式(10)相同,构建优化数学模型:

4.2 结果分析
基于第1年运行数据,对群体用户模型参数优化求解,得到对采用所有用户参数的统一最优解:等效坡度和质量分别为5.23%和1 779 kg。95%损伤期望水平与实际基本对应,如图15所示。基于此参数对用户第2年服役数据进行仿真验证,同样满足实际载荷的95%损伤期望水平,如图16所示。


图15 用户第1年损伤累积概率分布

图16 用户第2年损伤累积概率分布
图17为1号用户最优参数与统一参数的仿真转矩对比实际转矩变程的归一化分布,参数统一后的仿真转矩在变程小于0.8倍最大变程时分布与实际吻合度更高,在大于0.8倍时则相反。

图17 变程分布
结论证实了基于用户运行车速数据仿真构建可靠性目标载荷的研究方法的有效性。
5 结论
本文基于用户运行数据对道路坡度和整车质量模型参数进行优化,提出了电驱动系统可靠性目标载荷快速构建方法,并通过仿真与实际运行数据对比验证该方法的有效性。主要结论如下:
(1)根据整车数学模型建立仿真模型。由于工况的差异性,分析了在不同载质量与坡度状态参数下,用户仿真载荷的损伤精度、时域分布效果均不相同;在随机参数状态下,通过研究用户群体在不同时期仿真载荷的95%损伤水平与实际的误差,验证了用户不同时期工况剧烈程度有极强相关性。
(2)计算各等级参数下仿真转矩损伤,拟合得到损伤关于坡度和质量的函数关系式,验证了该函数的损伤计算精度。以此为基础,结合整车动力学平衡方程,构建不同用户的优化数学模型,对比实际转矩和空载无坡度参数下的仿真转矩,基于优化参数的仿真转矩损伤误差小,时域分布良好,95%损伤期望水平与实际基本一致。
(3)构建以参数统一、获取可靠性目标载荷为目的的数学优化模型,基于统一参数对整体用户进行转矩仿真,95%损伤水平基本对应实际,第2年服役数据同样满足条件;对比了用户时域分布,有较高精度。
本研究方法为电驱动系统可靠性目标载荷快速构建提供了一定参考,起到减少载荷样本采集量、加速电驱动系统可靠性评估与寿命预测的作用。
