基于Lasso回归和SVR模型的消费者信心指数的预测

顾艳文，刘媛华

(上海理工大学 管理学院，上海 200093)

0 引 言

中国的消费结构不断升级，消费亮点纷纷涌现，使得消费逐渐成为中国经济增长的主引擎。为了应对国内外动荡的经济形势，构建以国内大循环为主体的新发展格局，需要进一步加强消费对经济的拉动作用[1]。消费与消费者信心息息相关，增强消费的重要举措就是增强消费者信心。消费者信心指数是用来衡量消费者信心的指标，其反映了消费者对当前经济发展状况和未来经济发展预期的内心想法，科学有效的把握消费者信心指数的发展趋势，有助于了解消费者内心的真实感受，对有关部门制定宏观政策，促进经济健康发展具有重要意义。

消费者信心指数的获取通常是通过调查问卷的形式，但传统调查问卷的方法存在工作量大，时效性差，覆盖不全面等问题，所以国内外学者纷纷针对消费者信心指数进行预测研究。一些学者采用传统计量经济学模型，如杨娜、王静雅利用ARIMA模型预测消费者信心指数[2]；董现垒、Bollen Johan、胡蓓蓓利用谷歌趋势建立计量经济学模型，对消费者信心指数进行预测[3]；刘伟江、李映桥以网络搜索数据为基础，利用主成分分析法合成搜索指数，建立回归模型，预测台湾地区的消费者信心指数[4]。由于传统计量经济学模型通常适用于线性关系的情况，而消费者信心指数与变量之间的关系复杂多样，因此一些学者提出采用机器学习模型或者深度学习模型对其进行预测，如邹鸿飞、王建州建立了CEEMD-DEGWO-BPNN模型预测消费者信心指数[5]；唐晓彬、董曼茹、张瑞引入百度指数数据，建立长短时间记忆神经网络模型进行消费者信心指数的预测[6]。

Hanjo Odendaal、Monique Reid、Johann F.Kirsten认为在线情感指数对消费者信心指数具有预测作用，可为消费者信心指数的预测提供思路[7]。在以往的研究中，预测消费者信心指数所使用的影响因素也常为非结构化数据，然而非结构化数据的数据量较大，不能全部放入预测模型中建模，需要对变量进行筛选。本文采用对数据类型没有太多限制，且可以弥补最小二乘法和逐步回归法局部最优估计不足的Lasso回归对变量进行处理，同时采用既可以解决线性关系问题又可以解决非线性关系问题的机器学习模型——支持向量机回归，对消费者信心指数进行预测。

1 模型理论概述

1.1 Lasso回归

当数据特征较多时，为了防止模型的过拟合，常常需要对数据进行筛选降维。1996年国外学者Robert Tibshirani提出了Lasso回归。Lasso回归是一种缩减性估计，在回归过程中，可以将一些不重要的回归系数直接缩减为0，以此实现变量筛选的功能。Lasso回归可以降低模型训练时的计算量，因此在高维数据中得到广泛应用。Lasso回归的目标函数为式(1)：

(1)

其中，λ是惩罚项系数，控制着模型的复杂程度，λ越大对特征较多的模型惩罚力度越大，通过调整λ，最终可以获得特征较少的模型，以达到降维的目的。

1.2 SVR模型

SVR模型又称支持向量回归模型，其采用支持向量的思想，可将低维数据非线性映射到高维空间，从而在高维空间中对数据进行回归分析。支持向量回归模型的优点在于模型对数据的分布没有限制，可以有效解决小样本、非线性、高维度问题。SVR模型的目标函数为式(2)：

(2)

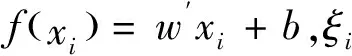
支持向量回归允许预测值和实际值之间存在一个合理的误差，即|yi-f(xi)|≤ε。根据拉格朗日函数的对偶性和极小值求解的方法，可以得到f(xi)中参数w与b的值，式(3)：

(3)

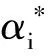
为了使模型能够解决非线性回归问题，引入核函数K(xi,xj)替换高维空间的内积，此时函数f(xi)可以表示为式(4)：

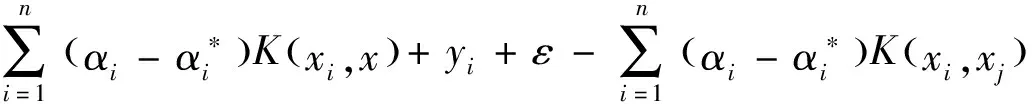
(4)

SVR模型对核函数的选择比较敏感，不同的核函数会使模型产生不同的结果。常用的核函数有多项式核函数(ploy核函数)、高斯核函数(rbf核函数)、Sigmoid核函数等，通过网格搜索的方法可以确定核函数的参数，从而使模型达到最好的效果。

1.3 消费者信心指数预测模型

由于Lasso回归的降维能力和SVR模型的优点，本文结合两个模型对消费者信心指数进行预测。首先，对数据进行预处理，提高数据质量；其次，对变量进行领先期数的确定，使选取的变量具有预测能力；然后利用相关系数选取与消费者信心指数相关的变量，再将新得到的数据集输入Lasso回归模型中降维，从而得到最终的预测变量；最后，把变量放入SVR模型中进行消费者信心指数的预测，并比较使用不同核函数模型的预测效果，从而确定最终的预测模型。消费者信心指数预测模型的构建思路如图1所示。

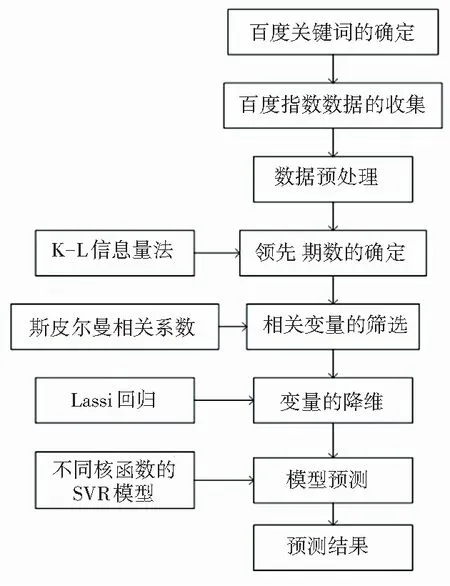
图1 消费者信心指数预测模型构建思路

2 消费者信心指数预测分析

2.1 数据来源

近年来，互联网快速发展，出现大量的非结构化数据，这些非结构化数据往往与经济现象之间存在某种联系，或多或少反映着真实的经济生活。因此，本文采用非结构化数据中的百度指数数据作为预测消费者信心指数的数据支撑，并通过文献参考和需求图谱的关键词推荐，选取了133个百度关键词，部分关键词见表1。百度指数数据分为移动端和PC端，而移动端的百度指数数据从2011年开始收录，故本文的数据从2011年开始收集，通过爬虫技术获取2011～2019年的PC端和移动端的百度指数。本文的研究对象为消费者信心指数，为保持数据的一致，选取了2011～2019年的月度数据作为本文的样本，其数据来源于中经网统计数据库。

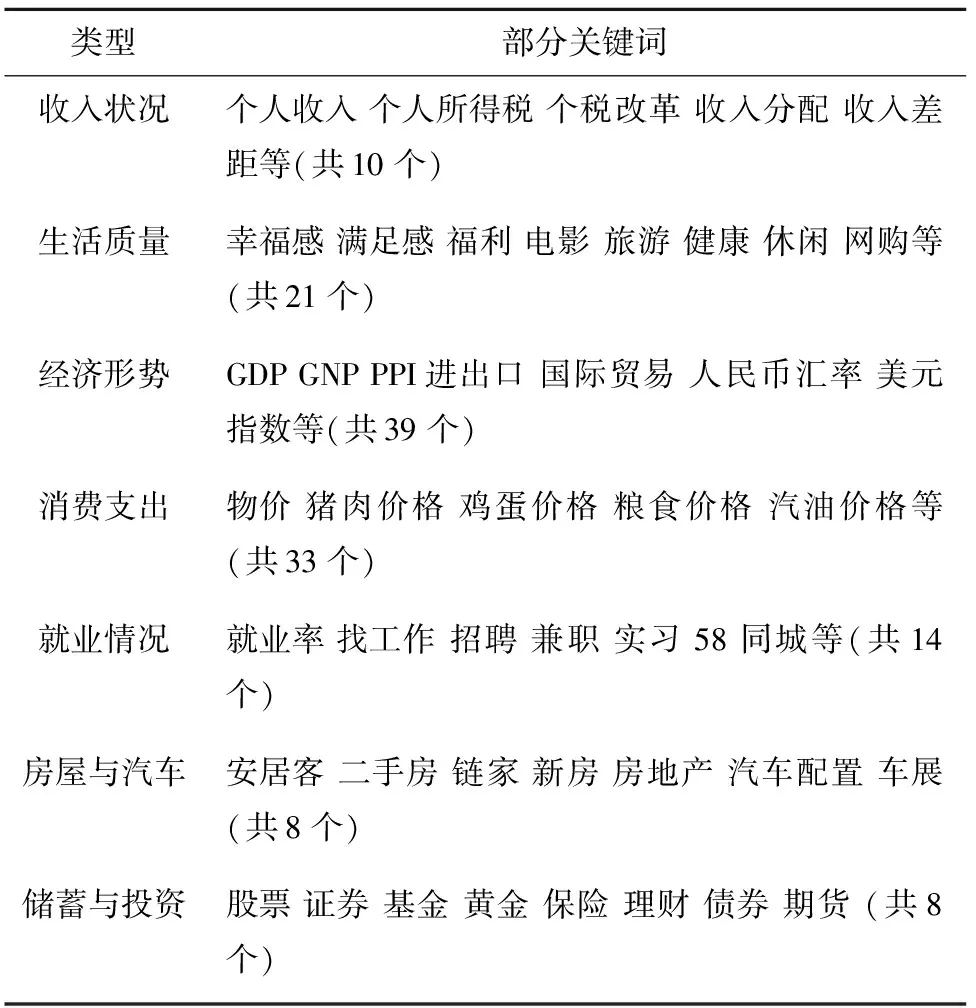
表1 部分关键词

2.2 数据预处理

百度指数数据是非结构化数据，可能会受到各种各样的干扰，存在噪声较大的问题，需要对其进行预处理。

第一步：异常值处理。百度指数数据会受到特殊事件的影响，导致出现异常值，而异常值会影响模型的预测效果，故需要对异常值进行处理。本文采用箱线图法对异常值进行判断，将筛选出的异常值用前后两期的均值进行替换。

第二步：去除长期趋势。随着近些年来互联网的高速发展，搜索引擎的使用频率也会随着时间的增加而增加，为了消除由于互联网发展导致搜索量的增加，需要寻找与本文研究对象相关性不大，且能代表互联网发展趋势的关键词[8]。因此计算选取的133个关键词与其百度指数的比值，以消除互联网长期发展趋势。通过参考相关文献，本文选取的关键词为百度。

第三步：合并数据。由于消费者信心指数为月度数据，故将百度指数的日度数据转为月度数据。

2.3 预测模型的建立

2.3.1 基于Lasso回归模型的变量的降维

本文选取的133个百度关键词并非都适合放入模型中作为变量进行预测，需要对其进行筛选。首先，通过K-L信息量法确定每个关键词的最佳阶数，将关键词领先阶数设为1～12阶，计算每个关键词领先1～12阶的K-L信息量，并从中选取K-L信息量最小值所对应的阶数作为该关键词的最佳阶数，根据最佳阶数将原始数据错位补齐；其次，计算错位补齐后的每个关键词和消费者信心指数之间的斯皮尔曼相关系数，并将阈值设为0.5，以此获得43个与消费者信心指数相关的关键词；最后，为了进一步减少模型的输入变量，提高模型的预测效果，建立Lasso回归模型对43个百度关键词进行筛选。

Lasso回归模型中的λ值是未知的，可以通过可视化方法大致确定λ的取值范围，然后通过交叉验证法确定最终的λ值。

λ和回归系数之间的关系如图2所示，每条折线图代表了每个变量。从图2可知，当λ的值大概在0.02～0.76之间时，绝大多数变量的回归系数趋于稳定。为确定准确的λ值，利用sklearn模块中的LassoCV类进行交叉验证，对每一个λ值，进行10重交叉验证，从而确定λ的值为0.141。以最佳λ值重新建立Lasso回归模型，最终筛选出6个百度关键词，分别为股票、赶集网、58同城、民宿、大众点评和个人所得税。表2是最终百度关键词的滞后阶数及斯皮尔曼相关系数。

表2 最终百度关键词

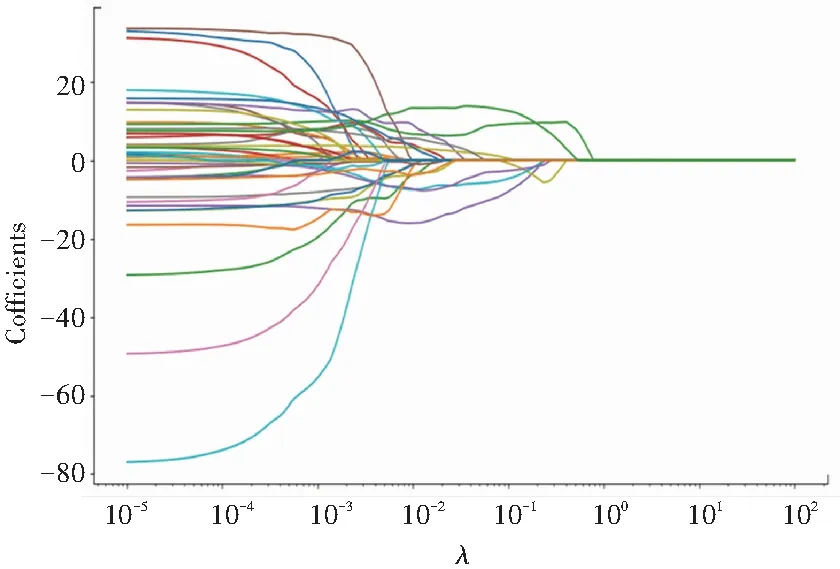
图2 λ与回归系数的关系

2.3.2 SVR预测模型

经过上述处理和变量筛选后，还剩余96期数据。将数据集按照7:3的比例划分训练集和测试集，并对其进行归一化处理，以消除不同数量级造成的影响。由于SVR模型的预测效果受核函数的影响较大，所以本文选取常用的多项式核函数高斯核函数，Sigmoid核函数进行建模，并采用网格搜索的方法对核函数参数、惩罚系数、损失函数参数进行寻优。SVR模型使用不同核函数的最终参数值见表3。

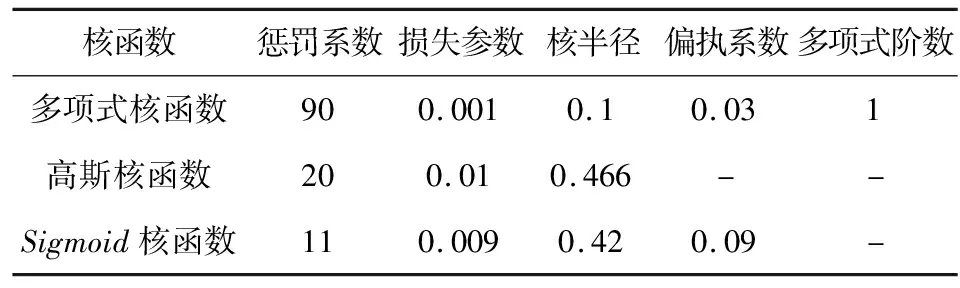
表3 模型参数值

根据网格搜索法得到的参数值，分别建立SVR模型，并对测试集进行预测，不同核函数预测结果如图3所示。

由图3可知，无论使用多项式核函数，高斯核函数还是Sigmoid核函数都可以对消费者信心指数进行大致的刻画，说明SVR模型对消费者信心指数具有一定的预测能力。但不同的核函数之间还存在一定的差异，为了选择更好的模型，对3种核函数的预测结果进行定量分析，采用均方根误差和平均绝对误差对其进行评价，评价结果见表4。

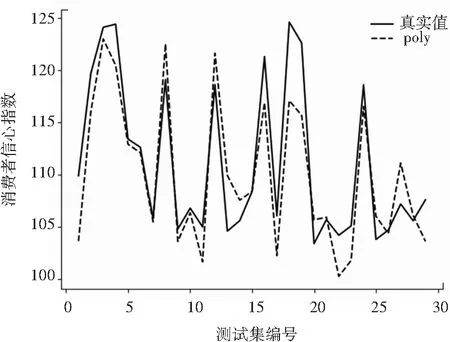
(a)多项式核函数

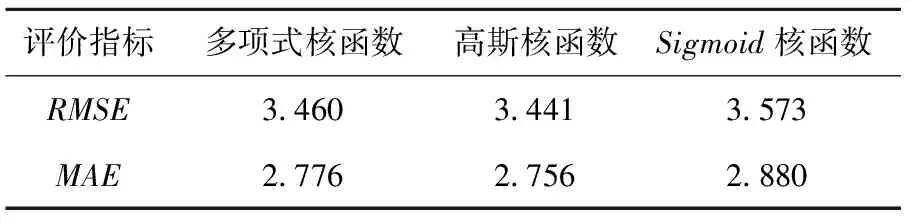
表4 不同核函数预测结果

由表4可知，多项式核函数和Sigmoid核函数的预测效果不如高斯核函数，当模型使用高斯核函数时，模型的均方根误差和平均绝对误差最小，分别为3.441和2.756；其次是多项式核函数，均方根误差为3.460，平均绝对误差为2.776；预测结果最差的是sigmoid核函数，均方根误差为3.573，平均绝对误差为2.88。

3 结束语

本文以非结构化数据中的百度关键词作为消费者信心指数的影响因素，将Lasso回归和SVR模型相结合，对消费者信心指数进行预测。同时，通过对比不同的核函数，认为在使用高斯核函数时，可以使消费者信心指数的预测效果达到最好。该方法有效预测了消费者信心指数，可以将其应用到其它经济指标的预测，从而更好的掌握经济指标的变化趋势。