《九章算术》中的代数部分

钱宝琮

《九章算术》是一部现有传本中最古老的中国数学经典著作.书中收集了二百四十六个应用问题和各个问题的解法，分别隶属于方田、粟米、衰分、少广、商功、均输、盈不足、方程、勾股九章.现在拟就问题的性质分成算术、几何、代数三类，介绍全书的主要内容.下面主要介绍《九章算术》中的代数部分，列出开平方与开立方、开带从平方、方程与正负数三个部分.

一、开平方与开立方

《九章算术》的少广章中提到了开平方法和开立方法，内容简明，依照两种方法进行演算也很方便.开平方法借用一根算筹来表示未知量的平方，开立方法借用一根算筹表示未知量的立方，这样就建立了筹式和代数方程之间的联系.开平方或开立方的各个演算步骤相当于解方程中求正根的过程.中国古代开平方、开立方的方法，不仅具有算术上的意义，更重要的是它们具有代数方面的意义.

少广章中的开方术说：“置积为实.借一算，步之，超一等.议所得，以一乘所借一算为法而以除.除已，倍法为定法.其复除，折法而下.复置借算步之如初.以复议一乘之，所得副，以加定法以除.以所得副从定法.复除，折下如前.”

例如，少广章中的第12题：一平方积为55225，求方边的长.布置算筹 ，这叫做“实”（被开方数）.取一算筹放在“实”的个位下边，如图1，这个筹式用代数符号表达出来是一个方程 .将这个“借算”向左移动，每一步移两位，移两步，便停在“实”的万位上，如图2.这样，“借算”所表示的数不是 ，而是 ，原方程就变为 ，可估算出 x 大于2而小于3，在“实”的百位上面放算筹ll，表示平方根的第一个数码.

以“议得”的2乘以10000得20000，摆在“实”的下面，“借算”的上面的算筹，叫做“法”.再以“議得”的2乘以“法”得40000，从“实”中减去40000，余数为15225，如图3.把“法”数加倍，向右边移一位，就变为4000，叫做“定法”.把“借算”向右边移两位，就变成100，如图4.这个筹式和代数方程 有同样的意义.

“议得”x 大于3而小于4，就把作3为平方根的第二个数码，将其放在“实”的十位上面.用3乘以100得300，将其放在“定法”的右边，加上“定法”得4300.用3乘以4300，从“实”中减去4300，余数为2325，如图5.再将300加上4300得4600，向右边移一位可得460，这是求平方根的第三个数码.把“借算”向右边移两位变为1，如图6.这筹式和代数方程 有同样的意义.

议得平方根的个位数 .用5乘以“借算”1得5，加上460得 465.用5乘以465，从“实”内减去它，没有余数.这样，我们就得到55225的平方根235.当被开方数是一个分数时，分母 b 开得尽，则 ，若开不尽，则 .

少广章中的开立方术说：“置积为实，借一算，步之，超二等.议所得，以再乘所借一算为法，而除之，除已，三之为定法.复除.折而下以三乘所得数置中行复借一算置下行步之，中超一、下超二位.复置议，以一乘中，再乘下，皆副，以加定法以定法除除已，倍下，并中从定法复除，折下如前.”

例如，少广章中的第19题：求1860867的立方根.要先布置算筹 ，将其作为“实”，并在“实”下面保留两个空层，把“算借”放在最下层.把这个“借算”从个位上移到千位上，再移到百万位上，如图8.这个筹式表示代数方程

通过估算可得 x1>1，将其作为立方根的第一个数码，在“实”的百位上面.用1乘以1000000得1000000，把它放在借算上面，称为“中行”.再用1乘以“中行”得1000000，将其放在“中行”的上面，“实”的下面，称为“法”.用1乘以“法”，从“实”内减去1000000，余数为860867，如图9.将其乘以3并向右移一位，将300000作为“定法”，“中行”乘以3并向右移两位可得30000.把“借算”向右移三位，可得1000，如图10.这个筹式表示方程

又“议得”x2>2，将其放在立方根的第二个数码上，并放在“实”的十位上，把“中行”乘以2得60000，将其放在“法”的右边.用2的平方乘以“借算”得4000，将其放在“中行”的右边.又将这两个数加上“定法”得364000.用2以乘“法”，从"实"内减去所得的结果，余数为132867，如图11.

用2乘以余下的数得8000，，加上“法”得432000，向右移一位得“定法”为43200.用3×2乘以“借算”得6000，加上“中行”得36000，向右移两位得360.把“借算”向右移三位，如图12.这个筹式表示方程  .

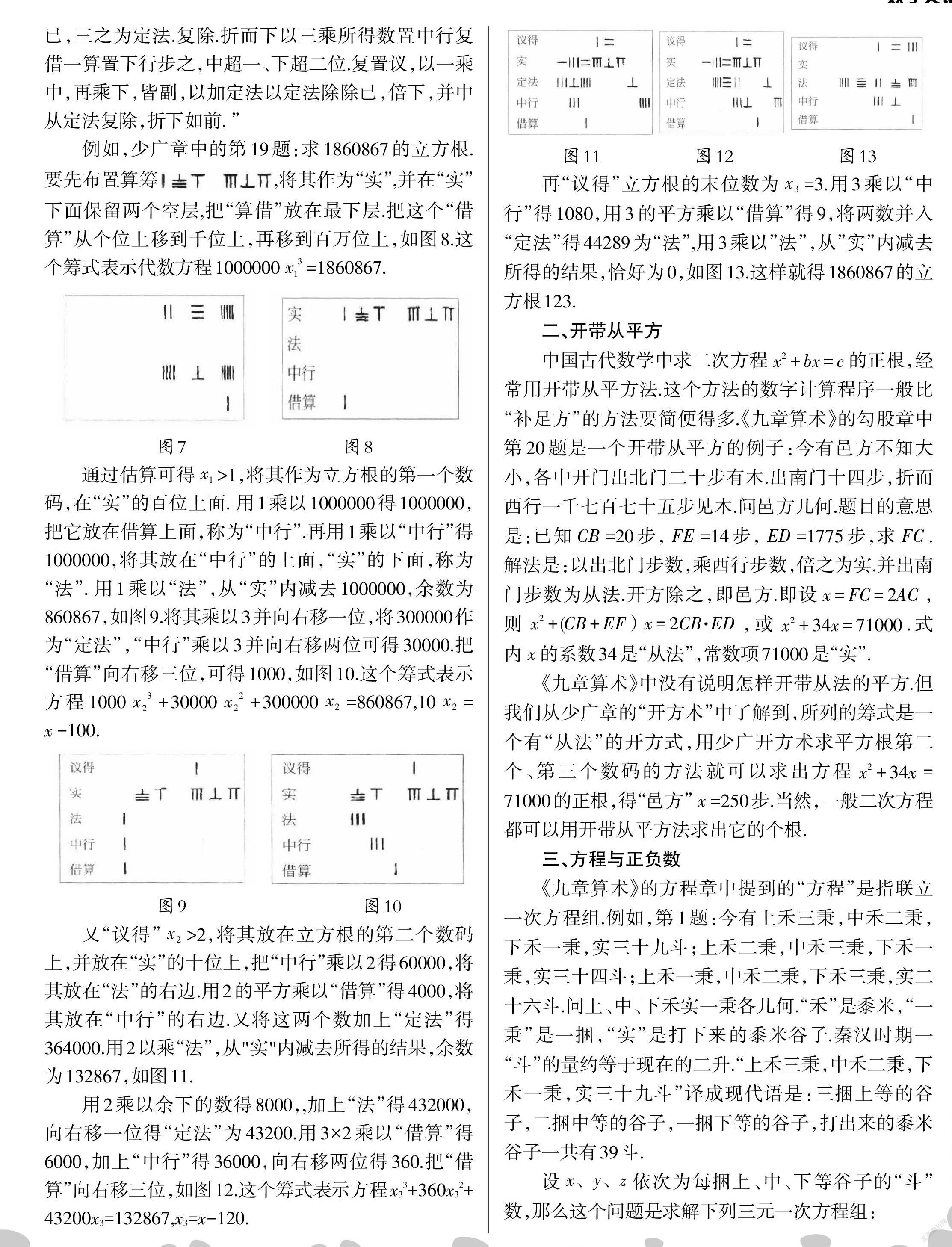
再“议得”立方根的末位数为 x3=3.用3乘以“中行”得1080，用3的平方乘以“借算”得9，将两数并入“定法”得44289为“法”，用3乘以”法”，从”实”内减去所得的结果，恰好为0，如图13.这样就得1860867的立方根123.

二、开带从平方

中国古代数学中求二次方程 x 2+ bx = c 的正根，经常用开带从平方法.这个方法的数字计算程序一般比“补足方”的方法要简便得多《.九章算术》的勾股章中第 20题是一个开带从平方的例子：今有邑方不知大小，各中开门出北门二十步有木.出南门十四步，折而西行一千七百七十五步见木.问邑方几何.题目的意思是：已知 CB =20步，FE =14步，ED =1775步，求 FC .解法是：以出北门步数，乘西行步数，倍之为实.并出南门步数为从法.开方除之，即邑方.即设 x = FC =2AC ，则 ，或 .式内 x 的系数34是“从法”，常数项71000是“实”.

《九章算术》中没有说明怎样开带从法的平方.但我们从少广章的“开方术”中了解到，所列的筹式是一个有“从法”的开方式，用少广开方术求平方根第二个、第三个数码的方法就可以求出方程 x 2+ 34x =71000的正根，得“邑方”x =250步.当然，一般二次方程都可以用开带从平方法求出它的个根.

三、方程与正负数

《九章算术》的方程章中提到的“方程”是指联立一次方程组.例如，第1题：今有上禾三秉，中禾二秉，下禾一秉，实三十九斗;上禾二秉，中禾三秉，下禾一秉，实三十四斗;上禾一秉，中禾二秉，下禾三秉，实二十六斗.问上、中、下禾实一秉各几何“.禾”是黍米，“一秉”是一捆，“实”是打下来的黍米谷子.秦汉时期一“斗”的量约等于现在的二升“.上禾三秉，中禾二秉，下禾一秉，实三十九斗”译成现代语是：三捆上等的谷子，二捆中等的谷子，一捆下等的谷子，打出来的黍米谷子一共有39斗.

设 x、y、z 依次为每捆上、中、下等谷子的“斗”数，那么这个问题是求解下列三元一次方程组：

用算筹布置起来，如图14，各行由上而下列出的算筹表示 x、y、z 的系数和常数项.三元一次方程组各项未知量的系数用算筹表示就像方阵，所以叫做“方程”.古代数学书中的“方程”和现在一般所谓方程是两个不同的概念.包含不止一个未知量的算式和联立方程组的概念.

以上面所举的第1题为例，依照方程章的“方程术”演算如下：

用（1）式内 x 的系数3乘以（2）式中的各项，得6x +9y +3z =102（4）

将（4）式“直除”（1）式，也就是两次减去（1）式的各项，得5y + z =24，（5）

同样，用（1）式内 x 的系数3乘以（3）式中的各项，得3x +6y +9z =78，（6）

将（6）式“直除”（1）式，得4y +8z =39，（7）

用算筹来演算得结果，如图15.

然后，用（5）式内 x 的系数5乘以（7）式中的各项，得20y +40z =195，（8）

将（8）式“直除”（5）式，得36z =99，（9）

将（9）式的两端同时除以9，得4z =11，（10），筹式如图16所示.在图16中，左行的未知量项只剩一项，用4除以11，即得 二斗.求 x 和 y ，还是用”遍乘直除”的方法.用（10）式的系数4乘以（5）式的各项，得20y +4z =96，再"直除"（10）式得20y =85，将（10）的两端同时除以5，得4y =17.（11）

用（10）式的系数4乘以（11）式的各项，得12x +8y +4z =156，“直除”（10）式，得12x +8y =145;再"直除"（11）式，得12x =111，将（11）的两端同时除以3，得4x =37（12），筹式如图17.

从图14到图17，方程组的算筹形式始终保持右、中、左三行，运筹演算相当便利.最后由（10）（11）（12）式，计算得 .

如果我们把上列消元过程中的四个筹算图写成现代代数学中矩阵的形式：

那么，利用直除法的方程术就是一种关于矩阵的计算《.九章算术》的方程章中有十八个联立一次方程组问题，其中二元的有八题，三元的有六题，四元的、五元的各有两题，都用上述的演算程序解答多元一次方程组.

该方法在印度最早出现于七世纪初婆罗门笈多（Brahmagupta，约628年）所著书中.在欧洲，最早提出三元一次方程组的解法是十六世纪中的法国数学家布丢（Buteo，1559年）《.九章算术》中的方程术，不但是中国古代数学中的伟大成就，在世界数学史上，也是一份最可宝贵的财产.

“方程”的每一行是由多项未知量和一个已知量所组成的等式，其中可能有相反意义的数量，由此产生正数与负数的对立概念.用“直除”法消元，当减数大于被减数时，也需要负数的概念来扩充减法的功用.因此，中国数学家在方程章里提出了正负数的不同表示法和正负数的加减法则.这在数学史上是一个无比的伟大成就.

正负术是指，同名相除，异名相益.正无入负之，负无入正之其异名相除，同名相益.正无入正之，负无入负之.这是方程章正负数加减法则的条文“.同名”“异名”就是现在所谓同号、异号.文中指出，两数同号则绝对值的差是余数的绝对值;两数异号则绝对值的和是余数的绝对值;减去的数如其是正数而大于被减数时，余数得负号;如其是负数而小于被减数时，余数得正号;两数同号则和数的绝对值等于两绝对值的和;两数异号则和数的绝对值等于两绝对值的差;当两數异号时，其中正数的绝对值较大则和数取正号，其中负数的绝对值较大则和数取负号.有了这正负数加减法则后，“直除”消元法的应用可以推广到任何联立一次方程组.在后世的“开方法”和天元术里，正负数加减法则也起着重要的作用.

——摘自《中国数学史》