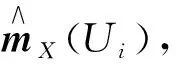一类条件协方差估计及其大样本性质

甘胜进

1. 福建师范大学 福清分校电子与信息工程学院，福建 福清 350300； 2. 台湾政治大学 统计学系，台北 11605

设p维随机变量X=(X1，X2，…，Xp)T，在给定协变量U=u条件下，考虑X的条件协方差矩阵，即

ΣXX(u)=cov(X|U=u)

当p=1时，条件协方差矩阵特殊化为条件方差Var(X|U=u)．条件方差及协方差函数的估计已在文献[1-6]中有较为详细讨论．依据

ΣXX(u)=E((X-mX(u))((X-mX(u))T|U=u)，其中mX(u)=E(X|U=u)

文献[7]通过极小化拟似然函数：

构造ΣXX(u)的估计量：

其中mX(u)的N-W核估计量为

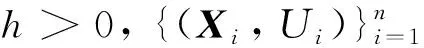
ΣXX(u)=E(XXT|U=u)-mX(u)mX(u)T

故一种显而易见的核估计量为

1 估计量的大样本性质

在导出估计量的渐近性质之前，一些限制性条件十分必要，它们经常在非参数核估计中用到，尽管它们不是最弱的，但能使证明变得简便．

(C1)U的边缘密度f(u)具有紧支集，并且在支撑集中，f(u)显著大于0，具有连续的二阶导数．

(C3)核密度函数K(v)满足以下条件：K(v)有界并且关于原点对称，K(v)≥0，

(C4) 存在常数c使得窗宽h→0，nh5→c，c>0，当n→+∞．

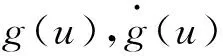
在类似于(C1)-(C4)的条件下，文献[7]得到条件协方差矩阵的核估计大样本形式：

(1)

其中：

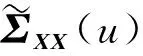
引理1令u为U的支撑的内点，在条件(C1)-(C4)下

逐点依分布收敛，其中

Σ1=(σj1，j2(u))p×p，σj1，j2(u)=f-1(u)K0Var(Xj1Xj2|U=u)

证令

Xi，j为X的第j个分量第i次观测，则有

不难得到

E(A1|U=Ui)=0，Var(A1)=Var(E(A1|U=Ui))+E(Var(A1|U=Ui))=

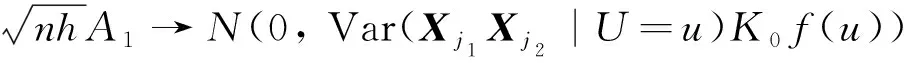
故有

类似以上讨论，

引理得证．

值得注意的是，尽管引理1给出核估计量的渐近正态性，但是这没有必要，只须将估计量写成以下相合形式：

(2)

其中

类似引理1过程，不难得到以下结果：

(3)

其中

通过以上讨论，由(2)式、 (3)式，根据条件(C1)-(C4)和Cr不等式[9]可得定理1．

定理1令u为U的支撑的内点，在条件(C1)-(C4)下，

逐点依分布收敛，其中

定理2给出逆协方差矩阵估计量的大样本性质．

定理2设u为协变量U的内点，在条件(C1)-(C4)下，

证由定理1，根据文献[10]讨论，假设

左边是

故

定理得证．

同理可得

2 随机模拟

借助文献[7]采用留一交叉验证拟似然函数来选择最优窗宽：

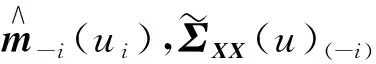
表1 模型1下协方差矩阵的两种估计量偏差比较

表2 模型1下逆协方差矩阵两种估计量偏差比较

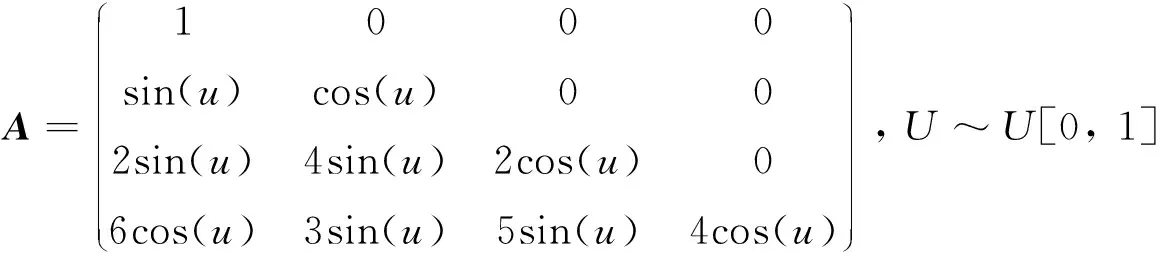
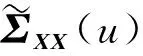
表3 模型2下协方差矩阵的两种估计量偏差比较

续表3

表4 模型2下逆协方差矩阵两种估计量的偏差比较

3 结 语