混合偏正态数据下中位数回归模型的参数估计

曾 鑫，吴刘仓，曹幸运

(昆明理工大学 理学院，云南 昆明 650093)

0 引 言

在计量经济学文献中，混合回归模型也称为转换回归模型，它为研究来自两个或两个以上总体的数据提供了有效的工具. 自Goldfeld等[1]首次提出有限混合回归模型以来，混合回归模型在生物学、医学、经济学、环境科学、抽样调查和工程技术等领域得到了广泛的应用，可参考文献[2-5].现实世界中, 我们搜集到的数据往往不严格服从正态分布, 当数据存在偏斜时, 我们再使用正态分布、t分布或Laplace分布等对称分布来描述它们是不合理的.因此, 自Azzalini[6]首次提出偏正态分布及其性质以来, 偏正态分布比传统的正态分布更加广泛地应用于实际数据的拟合, 关于偏正态分布的更多细节可以参考[7].基于偏正态分布，吴刘仓等[8]研究了联合位置与尺度混合专家回归模型的参数估计，马婷等[9]基于Gauss-Newton迭代法研究了联合位置、尺度与偏度模型的极大似然估计，李世凯等[10]研究了偏正态数据下混合非线性回归模型的参数估计.

以上文献仅局限于均值模型的参数估计，目前还没有文献研究混合偏正态数据下中位数回归模型的参数估计，为了提高偏正态数据下参数估计的灵活性，本文研究了混合偏正态数据下中位数回归模型的参数估计.模拟和实例研究结果显示该模型的方法是有效的.

1 混合偏正态中位数回归模型

1.1 偏正态分布

如果一个随机变量Y的概率密度函数[6]可以表示为：

(1)

其中：μ为位置参数，σ为尺度参数，λ为偏度参数，则称随机变量Y服从偏正态分布，记为Y～SN(μ,σ2,λ).其中ø(·)和Φ(·)分别为标准正态分布的密度函数与分布函数.易知，当偏度参数λ=0时，Y的密度函数退化为正态分布的密度函数，即此时偏正态分布SN(μ，σ2，λ)退化为正态分布N(μ，σ2)；当λ>0和λ<0分别称为右偏和左偏.

同时，若随机变量Y服从偏正态分布，则Y的随机表达形式为：

(2)

(3)

即偏正态分布可以分层表示为一个截尾正态分布R和一个条件正态分布Y|(R=r)，其中截尾正态分布TN(0,1;(0,∞))表示一个标准正态分布在区间(0,∞)的截尾，概率密度函数可表示为：

偏正态分布的随机表达形式和分层表达形式将分别在Monte Carlo模拟和EM算法中使用到.此外，Azzalini等[7]提出偏正态分布的均值和众数可以表示为：

Mean(Y)=μ+μ0(λ)σ,Mode(Y)=μ+m0(λ)σ

其中：

并且：

由均值、中位数和众数之间的数量关系|mean(Y)-mode(Y)|≈3|mean(Y)-median(Y)|，有：

(4)

1.2 混合偏正态中位数回归模型

为了研究概率密度函数(1)的解释变量与中位数之间的关系，我们提出下列混合偏正态数据下的中位数回归模型：

(5)

(6)

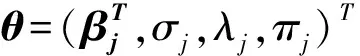
1.3 模型的可识别性

模型的可识别性是统计推断的重要部分，这也是混合回归模型的关键问题. Titterington等[11]提出连续分布的有限混合在大多数情况下都是可识别的.本文中，模型：

可识别的充要条件为m=m*，θ=θ*,i=1,2,…,n;j=1,2,…,m,其中μij由(6)定义.对于偏正态分布，不同的参数对应不同的偏正态分布，即分布可识别，则模型可识别.

2 参数估计的EM算法

EM算法可以极大化任意分布有限混合的对数似然函数，可参考Dempster等[12].记潜变量zi=(zi1,zi2,…,zim)，其中

通过使用偏正态分布的分层表达(3)，我们得到下列混合偏正态分布的分层表达形式：

(7)

其中,Z服从多点分布.因此，当zij=1时(Y,R)的联合密度为：

其中,eij=yi-μij.根据贝叶斯准则，可得：

因此有：

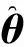
E-步：计算

求替代函数如下：

Q(θ|θ(t))=E[l(θ|Ycom)|Yobs,θ(t)]=Q1+Q2+Q3+Q4

(8)

式(8)中:

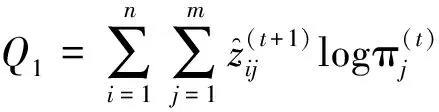
且：

M-步：给定初值θ(0)=(β(0)T,σ(0),λ(0),π(0)),θ(1)=(β(1)T,σ(1),λ(1),π(1)).基于两点步长梯度法[13]给定下列梯度迭代以更新：

θ(t+1)=θ(t)+s(t)G(θ(t))

(9)

其中:得分函数G(θ(t))和步长s(t)定义为：

计算得分函数为：

其中:

其中：

且：

3 Monte Carlo模拟

为了评价上述参数估计方法的估计效果，需要对有限样本性质进行模拟研究.为了节省空间, 我们只讨论混合偏正态中位数回归模型, 参数的估计精度使用均方误差来衡量，定义为：

表1 混合偏正态中位数回归模型的模拟结果

从表1可以得出以下结论：

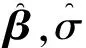
2) 对于给定的样本量n，当混合比例时1=2=0.5时，两个子聚类估计的均方误差(MSE)接近；当混合比例1=0.35，2=0.65时，子聚类2估计的均方误差(MSE)比子聚类1估计的均方误差(MSE)小.

以上结论表明，本文提出的混合偏正态中位数回归模型及使用的EM算法对参数的极大似然估计取得了较理想的效果.

4 实例分析

在本节中，我们利用Cook和Weisberg[15]所测量的数据集来论证本文所提出的模型和方法的实际应用效果. 数据集包括来自澳大利亚体育学院的100名女性运动员和102名男性运动员的身体质量指数(BMI)数据，其中响应变量为BMI(y)，解释变量为红细胞计数(x1)，血浆铁蛋白浓度(x2)，皮肤褶皱和(x3)，身体脂肪百分比(x4).根据不同性别的数据特征，我们将数据分为两个子聚类.图1显示了男性运动员和女性运动员的直方图，容易看出数据右偏且不存在尖峰厚尾的情况，近似服从偏正态分布.

图1 男性运动员和女性运动员BMI直方图Fig.1 Histogram of BMI data for male and female athletes

我们考虑下列混合偏正态中位数回归模型，其中子聚类1(男性)所占比例为1=102/202≈0.505，子聚类2(女性)所占比例为2=100/202≈0.495.

基于第2节提出的方法，分别使用两个子聚类的数据和总的数据，经算法迭代收敛，表2给出了实际数据下混合偏正态中位数回归模型的参数估计结果.

表2 BMI数据的模型参数估计结果

由表2可以得出，使用三种数据所估计的参数是存在差异的.从回归系数的正负来看，红细胞计数(x1)和身体脂肪百分比(x4)与女性运动员BMI呈正相关，而与男性运动员BMI呈负相关；血浆铁蛋白浓度(x2)与男性运动员BMI呈正相关，而与女性运动员BMI呈负相关；皮肤褶皱和(x3)与男女性运动员都呈正相关.从系数的大小来看，各解释变量对男性运动员和女性运动员BMI的影响程度也不相同.因此，若不考虑对来自异质总体的数据进行分类研究，得到的结果可能是不准确甚至是错误的.

5 结 论

与其他文献所提出的模型相比，本文提出的模型有以下方面的优势：

1)建立的混合回归模型可以同时对各异质总体进行参数估计，这一点在实际问题中有很重要的意义.

2)基于偏正态数据的特征，对中位数进行建模并进行参数估计，相比于传统的均值模型的参数估计更加灵活.

模拟研究和实例分析结果表明：与现有的模型和参数估计方法相比，本文提出的混合偏正态中位数回归模型具有较大的灵活性，能够很好的结合实际数据进行分析.本文提出的模型及参数估计方法具有实用性和有效性.