基于流量优化的可靠服务功能链部署方法
2021-11-11孟相如康巧燕赵文文
阳 勇, 孟相如, 康巧燕, 赵文文
(空军工程大学信息与导航学院, 陕西 西安 710077)
0 引 言
随着互联网技术的发展,传统网络僵化的弊端逐渐凸显,其软件与硬件紧耦合的架构越来越难以满足用户的需求[1-2]。在传统网络中,基于专有硬件的网络功能导致诸多问题,比如网络升级换代需要巨大开销、可管理性差、可扩展性差等[3-5]。网络功能虚拟化(network function virtuali-zation,NFV)是解决上述问题的下一代网络重要技术之一,其通过解耦硬件物理设备与运行于其上的网络功能,实现网络功能的灵活部署、软硬件的发展周期分离以及网络功能的动态扩展[6-8]。利用NFV技术,网络功能可以当成一个普通软件的实例,根据需求动态部署在网络中不同位置而无需重新安装新的硬件,在增加灵活性的同时极大地降低了运营商的成本[9-11]。
在NFV环境的网络中,服务功能链(service function chain,SFC)部署是实现网络业务的基础,部署过程中的资源开销很大程度上决定了运营商的成本,部署后的可靠性严重影响网络功能的稳定性,进而影响对用户的服务质量(quality of service,QoS),因此SFC部署问题得到了许多学者的关注[12-29]。文献[12]在虚拟网络功能(virtual network function,VNF)部署阶段,利用PageRank算法进行节点排序,在保证端到端时延的同时提高了SFC的可靠性,但未考虑资源开销的优化。文献[13-16]通过备份的方式提高SFC的可靠性,其中文献[13]对VNF进行联合备份,将SFC部署问题构建成整数线性规划模型,在优先满足SFC可靠性的同时优化了资源配置;文献[14]对链路进行备份,基于路径分割对虚拟链路进行多路径映射,以保证链路的可靠性。但此类方法因为冗余备份增加了运营商的成本。文献[17-21]提出迭代算法进行VNF部署,其中文献[17]采用基于改进遗传模拟退火算法的VNF部署策略优化了端到端时延;文献[18]在对SFC构建与部署进行双层编码的基础上,利用改进遗传粒子群算法优化了请求接受率与资源开销;文献[19]提出改进遗传算法进行VNF部署,并结合物理节点保护机制,提高了底层网络资源利用率和SFC的生存性。但这此类方法都需通过反复迭代才能求解,难以实现VNF的快速部署。文献[22]采用三阶段递进的方式部署VNF,首先将VNF部署到可靠性最高的节点上,然后调整部署方案实现对负载的优化,最后调整部署方案缩短大带宽虚拟链路部署到底层网络后的物理长度,该方法提高了SFC的可靠性,但未考虑端到端时延。文献[23-27]采用机器学习算法进行VNF部署,对SFC的性能有较大优化,但依赖足够多的准确数据对模型进行训练。文献[28]提出可以采用聚合的方式部署VNF,但未进一步研究具体的聚合方法。文献[29]根据功能约束与资源约束聚合VNF,未考虑VNF对链路流量的影响。
针对上述问题,本文提出基于流量优化的可靠服务功能链部署(reliable service function chain deployment based on traffic optimization,TO-RSFCD)方法。首先根据虚拟链路的带宽需求变化对VNF进行聚合处理,使聚合的VNF部署到底层网络后大带宽虚拟链路上的流量成为服务器的内部流量,达到降低链路开销的目的。然后综合考虑物理节点的可靠性、综合时延以及拓扑属性,利用离差最大化的多指标决策算法对满足资源需求的物理节点进行评价并排序,评价过程中赋予对排序作用大的评价指标更高权重。同时通过链路约束降低流量乒乓效应,依次将聚合后的VNF部署在排序最靠前的节点上。最后采用k-最短路径算法完成虚拟链路的部署。实验表明,TO-RSFCD方法在保证SFC可靠性的基础上,对映射成功率、平均收益开销比、端到端时延以及带宽开销进行了较大优化。本文的主要贡献有:
(1) 根据虚拟链路的带宽需求变化对VNF进行聚合,使聚合的VNF部署到底层网络后大带宽需求链路上的流量变为服务器的内部流量,优化了资源开销;
(2) 提出节点综合时延和拓扑就近度指标,前者量化节点及其相邻链路所产生的时延,后者量化节点与源、目的端点之间最短路径的拓扑属性,实现了算法对底层网络的拓扑与时延感知;
(3) 采用离差最大化多指标决策算法对物理节点进行评价,对排序作用大的评价指标赋予更高权重,实现了权重的自适应设定;
(4) VNF部署过程中设置链路约束条件,降低了流量的乒乓效应。
1 网络模型及问题描述
1.1 网络模型
物理网络用一个加权无向图G=(N,E)表示,其中N为物理节点的集合,E为物理链路的集合。每个物理节点上附着一至多个服务器,能够用来实例化VNF。节点ns∈N的剩余可用计算资源为Cal(ns),可用存储资源为Mem(ns),可用转发资源为For(ns),实例化VNF后产生的时延为d(ns),可靠性为r(ns)。链路es∈E的剩余可用带宽为b(ns),时延为d(es)。
SFC请求用一个七元组(I,O,D,T,R,V,L)表示,其中I为源端点,O为目的端点,D为SFC的最大允许时延,T为SFC的生存时间,R为SFC的可靠性要求下限,V为组成SFC的VNF集合,L为组成SFC的虚拟链路集合。集合V={v1,v2,…,vn}中的元素vi表示SFC的第i个VNF,其计算资源需求为Cal(vi),存储资源需求为Mem(vi),转发资源需求为For(vi),带宽改变因子为η(vi),其中带宽改变因子定义为VNF流量的流出带宽与流入带宽之比。集合L={l0,l1,…,ln}中的元素li为vi到vi+1之间的虚拟链路。当i=0时,li为源端点I到v1之间的虚拟链路,当i=n时,li为vn到目的端点O之间的虚拟链路。用b(li)表示li的带宽需求,则b(li)的计算公式为
(1)
1.2 优化目标
用xi, j表示vi是否部署到物理节点nj上,yi, j表示li部署到底层网络后是否经过物理链路ej。令集合φ=(Cal, Mem, For),k∈φ表示计算、存储、转发资源中任意一种资源。则SFC部署到底层网络后,资源开销的计算公式为
(2)
式(2)的第一部分表示节点的计算、存储与转发资源开销,第二部分表示链路的带宽开销。本文旨在保证SFC可靠性和时延要求的基础上,对资源开销进行优化,优化目标为
Goal=min(Cost)
(3)
SFC的部署过程中约束条件如下:
(4)
(5)
(6)
(7)
(8)
(9)
(10)
式(4)表示每一个VNF都能在底层网络部署,但只能部署到一个物理节点上。式(5)表示每一条虚拟链路都能在底层网络部署,且能部署在一条或多条物理链路上。式(6)表示每一条物理链路被同一条SFC的虚拟链路最多部署一次,这是为了防止乒乓效应,其中乒乓效应指流量在两个网络节点间来回传输。式(7)表示VNF的任意一种资源需求都不能超过所部署节点的剩余可用资源。式(8)表示虚拟链路的带宽需求不能超过所部署链路的剩余可用带宽。式(9)表示SFC的时延不能超过所允许的最大时延,不等式的左边第一部分表示节点产生的时延,第二部分表示链路时延。式(10)表示SFC必须满足可靠性要求,不等式的左边表示SFC的可靠性。本文只考虑服务器的可靠性,当节点作为转发节点时,由于其上附着的服务器没有被SFC使用,所以其可靠性不计入SFC的可靠性中。
1.3 问题描述
从资源开销的组成部分分析,由于每个VNF只能部署在一个物理节点上,所以计算、存储与转发资源的开销与需求相等,无法对其进行优化。而每一条虚拟链路能够部署在一条或多条物理链路上,所以带宽开销必定大于或等于带宽需求,能够对其进行优化。图1是同一SFC在相同物理网络拓扑下的3种不同部署方法,箭头处数字代表初始带宽,VNF处数字代表带宽改变因子。

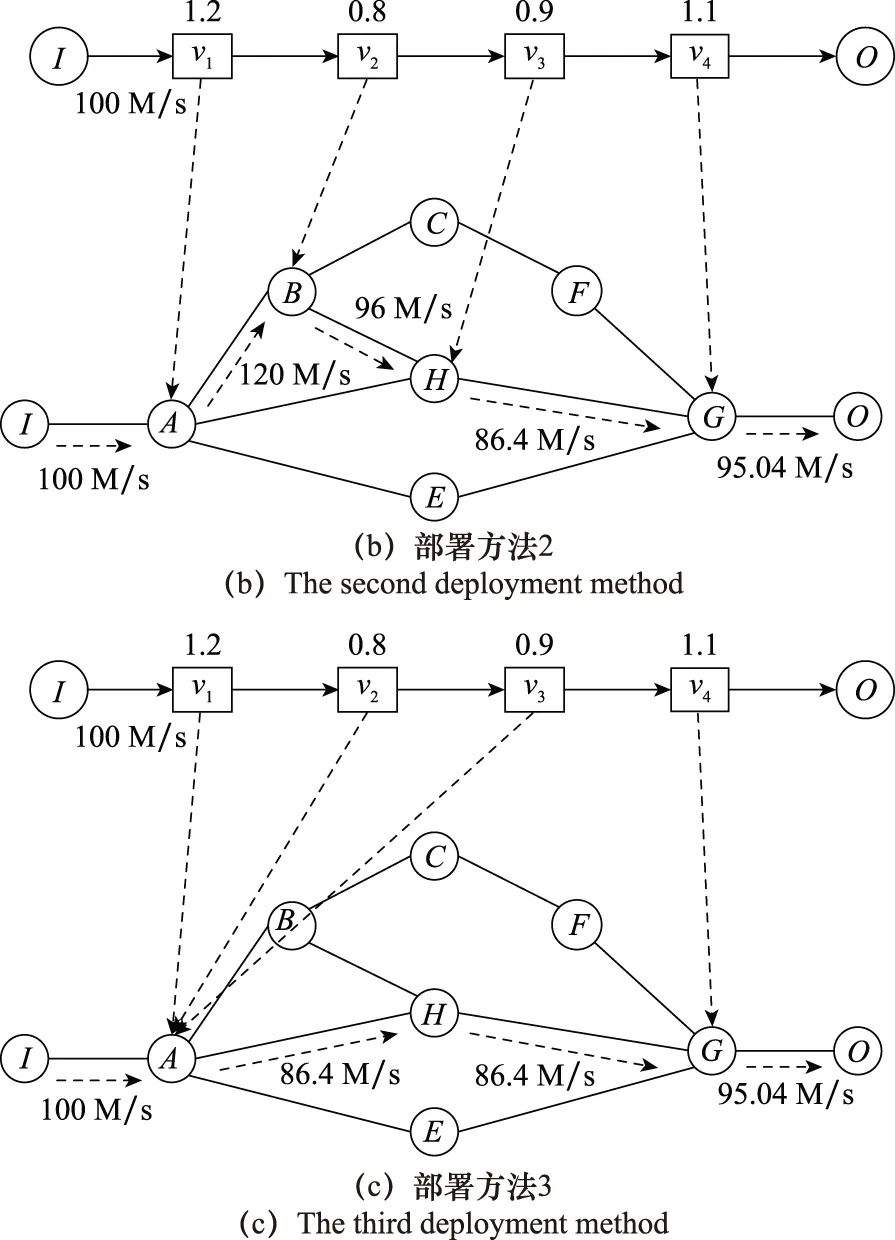
图1 不同VNF部署方法对比Fig.1 Comparison of different VNF deployment methods
与方法1相比,方法2通过链路约束避免了流量在节点B与节点H之间来回传输(即乒乓效应),方法3在避免乒乓效应的基础上,将某些VNF进行了聚合部署。经计算,方法1的带宽开销为583.84 M/s,方法2的带宽开销为497.44 M/s,方法3的带宽开销为367.84 M/s,方法2和方法3相较于方法1对带宽开销进行了较大优化。
假设每个物理节点的可靠性为0.95,由于方法3中只在两个节点上部署VNF,SFC的可靠性为0.952=0.902 5。而另外两种方法在4个节点上部署VNF,SFC的可靠性为0.954=0.814 5。对比可见,方法3的SFC可靠性也得到了提高。因此,在部署SFC时,以一定规则对VNF进行聚合处理,并尽可能减少流量的乒乓效应,则能在提高SFC可靠性的同时达到优化带宽开销的目的。
2 基于流量优化的可靠服务功能链部署方法设计
2.1 基于带宽需求变化的VNF聚合算法
NFV环境中存在3类VNF,第1类是带宽改变因子大于1的VNF,比如数据加密、编码等,经此类VNF处理后,SFC的带宽会增大。第2类是带宽改变因子等于1的VNF,比如QoS监视、入侵检测等,经此类VNF处理后,SFC的带宽不会发生变化。第3类是带宽改变因子小于1的VNF,比如防火墙、数据解密等,经此类VNF处理后,SFC的带宽会减小。为达到优化带宽开销的目的,就必须在保证VNF编排顺序不变的前提下,将带宽改变因子小于1的VNF在物理网络中靠前部署,带宽改变因子大于1的VNF靠后部署。
本算法的中心思想是针对所有带宽改变因子大于1的VNF,将编排在其后但在下一个带宽改变因子大于1的VNF之前的所有VNF与其进行聚合,聚合的VNF将部署到同一个物理节点上,达到将带宽改变因子小于1的VNF靠前部署的目的,并使大带宽需求链路上的流量变为服务器的内部流量,如图2所示。
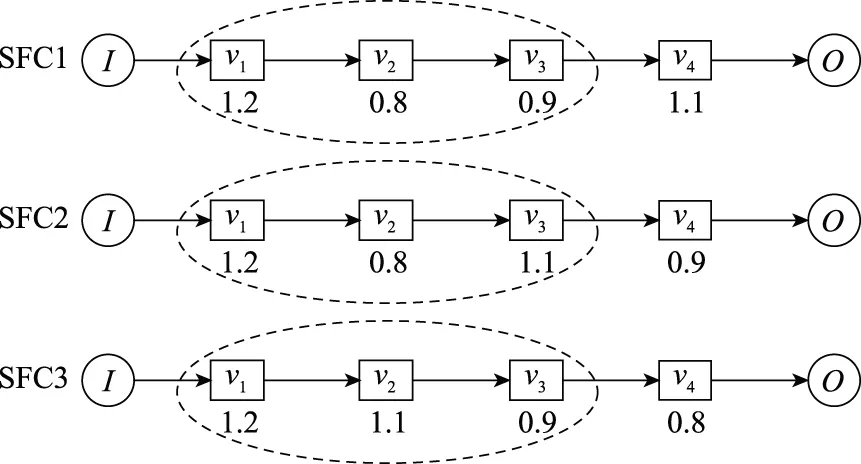
图2 基于带宽需求变化的VNF聚合算法案例Fig.2 A case study of VNF polymerization algorithm based on bandwidth demand changes
以SFC1为例,v1和v4是带宽改变因子大于1的VNF,v2和v3编排在v1之后,v4之前,所以将v2和v3与v1进行聚合。聚合的VNF将部署到同一个物理节点上,其中流入该物理节点流量的带宽为SFC1的初始带宽,流出该物理节点流量的带宽为经v1、v2和v3依次处理过的带宽,是一个较小的值。而仅经v1处理过的大带宽流量成为了该物理节点上所附着服务器的内部流量。SFC2和SFC3的聚合规则同理。算法的具体步骤如下所示。

算法 1 基于带宽需求变化的VNF聚合算法输入: VNF集合V,V中元素所对应的带宽改变因子集合η输出: 聚合后的VNF集合V′1 for V中每一个元素vi 2 if η(vi)>13 将vi的编排位置放入集合Temp中;4 end if5 end for6 if η(vi)≤17 将V中前Temp-1个VNF进行聚合,并赋值给v′1; 8 for i=2: |Temp|9 将V中第Temp(i-1)到Temp(i)-1个VNF进行聚合,并赋值给v′i;10 end for11 将V中第Temp(i)及之后的所有VNF进行聚合,并赋值给v′ i+1;12 else13 for i=|Temp|-114 将V中第Temp(i)到Temp(i+1)-1个VNF进行聚合,并赋值给v′i;15 end for16 将V中第Temp(i+1)及之后的所有VNF进行聚合,并赋值给v′ i+1;17 end if18 return V′
聚合后VNF的计算、存储与转发资源需求等于聚合前各VNF的同类资源需求之和,带宽改变因子等于聚合前各VNF的带宽改变因子之积。
2.2 基于离差最大化的VNF部署算法
对SFC中VNF进行聚合处理后,再对聚合的VNF进行部署。本算法的中心思想是在对底层网路进行拓扑与时延感知的基础上,利用离差最大化的多目标决策算法对物理节点进行评价并排序,每次按照编排顺序部署聚合后的VNF时,依据资源约束与链路约束筛选物理节点,再从筛选出的物理节点中选择排序靠前的部署VNF。对物理节点进行评价的指标有节点可靠性、节点综合时延、节点拓扑就近度和节点源端距。
节点可靠性采用固有可用度[30]进行表示,其定义为
(11)
式中:MTBF表示节点的平均故障间隔;MTTR表示平均修复时间。节点可靠性越高,越有利于靠前排序。
定义 1节点综合时延是对节点及其相关联链路所产生时延的综合度量,能反映选取该节点部署VNF后对SFC时延的影响,是算法实现对底层网络时延感知的关键指标,其计算公式为
(12)
式中:d(ns)表示节点ns所产生的时延,包括排队时延、处理时延与发送时延;E(ns)表示与ns相关联的物理链路集合,|E(ns)|表示集合E(ns)中元素的个数;d(es)表示链路es所产生的时延,包括传播时延;α与β为权重因子,本文中均设为1。节点的综合时延越小,越有利于靠前排序。
定义 2节点拓扑就近度表示节点与源目端点之间最短路径的拓扑紧密程度,能反映选取该节点部署VNF后对SFC物理长度的影响,是算法实现对底层网络拓扑感知的关键指标,其计算公式为
(13)
式中:TD(ns)表示ns的度数,数值上等于|E(ns)|;hop(ns,I)表示ns与源端点之间的最短跳数;hop(ns,O)表示ns与目的端点之间的最短跳数。采用节点拓扑就近度作为评价指标能缩短SFC的物理长度,节点的拓扑就近度越大,越有利于靠前排序。
节点源端距表示节点与源端点之间的最短跳数,即hop(ns,I)。采用节点源端距作为评价指标能实现带宽改变因子小于1的VNF尽可能靠前部署,节点源端距越小,越有利于靠前排序。
采用离差最大化的多指标决策算法计算每个物理节点ns的评价度S(ns),并利用S(ns)对各物理节点进行排序,然后依据VNF编排顺序对各VNF进行部署。离差最大化的多指标决策算法步骤如下。
步骤 1根据评价指标类型构造规范化决策矩阵(Zij)m×n。假设有m个评价对象,表示不同的物理节点,每个物理节点有n个评价指标,记第i个物理节点的第j个评价指标值为aij。值越大越有利于节点靠前排序的评价指标为效益型评价指标,如节点可靠性与拓扑就近度;值越小越有利于节点靠前排序的评价指标为成本型评价指标,如节点综合时延与源端距。效益型评价指标在决策矩阵中的值为
(14)
成本型评价指标在决策矩阵中的值为
(15)
式中:max(a*j)表示第j个评价指标的最大值;min(a*j)表示第j个评价指标的最小值。
步骤 2根据离差最大化方法计算各评价指标的最优加权向量W*。设评价指标的加权向量为W=[w1,w2,…,wn],则在W作用下规范化决策矩阵为
(16)
如果某评价指标的值对所有物理节点均无差异,则其对节点排序不起作用,应将其权重设为0。反之若某评价指标的值对所有物理节点有较大差异,则其对节点排序起重要作用,应将其权重设为较大值。在当前权重下,第i个物理节点的第j个评价指标与其他物理节点的离差为dispij(w),计算方式为
(17)
第j个评价指标的总离差为dispj(w),其表示就第j个评价指标而言,所有物理节点与其他物理节点的总离差,计算方式为
(18)
据前面分析,加权向量W的选择应使所有评价指标的总离差最大,因此构造目标函数为
(19)
其中,约束条件为
(20)

(21)
步骤 3根据最优加权向量作用下的决策矩阵计算各物理节点的综合评价度S(ns)。最优加权向量作用下的决策矩阵为
(22)
第i个物理节点的综合评价度为
(23)


算法 2 基于离差最大化的VNF部署算法输入: 经VNF聚合处理后的SFC=(I,O,D,T,R,V′,L′),物理网络G=(N,E)输出: VNF_Embedding_List1 for N中每一个物理节点ns2 利用离差最大化多指标决策算法计算综合评价度S(ns);3 end for4 利用S(ns)对N中物理节点进行排序;5 for V′中每一个v′i6 从N中筛选出满足其计算、存储与转发资源需求的节点集合Ф(v′i);7 if Ф(v′i)为空8 return VNF_EMBEDDING_FAILED9 else10 从Ф(v′i)删除满足hop(ns, O)>hop(ns(vi-1′), O)的物理节点;11 if Ф(v′i)为空12 return VNF_EMBEDDING_FAILED13 else14 将v′i部署到Ф(v′i)中排序最靠前的物理节点上,并将映射关系存入VNF_Embedding_List中;15 更新各物理节点剩余资源;16 end if17 end if18 end for19 计算SFC的可靠性;20 if SFC的可靠性不满足可靠性要求下限R21 return VNF_EMBEDDING_FAILED22 else 23 return VNF_Embedding_List34 end if
2.3 虚拟链路部署
VNF部署完毕后,首先在物理拓扑中删除不满足带宽需求的物理链路,然后利用k-最短路径算法在剩余拓扑中部署虚拟链路,最后根据VNF所部署物理节点产生的时延与虚拟链路所部署物理链路的时延计算出SFC的端到端时延,若该时延小于最大允许时延D,则SFC部署成功,否则部署失败。
在VNF部署阶段,TO-RSFCD对物理节点进行评价的时间复杂度为O(|N|);在链路部署阶段,k-最短路径算法的时间复杂度为O(k|N|(|E|+|N|lg|E|))。
3 算法性能评估与分析
为评估本文所提方法的性能,利用Matlab对其进行仿真并与基于QoS保障的服务功能链动态部署算法[12]、可靠感知与资源优化的虚拟网络功能部署方法[22]进行对比。同时,为验证VNF聚合部署的优势,设置了一种本文所提方法的对照方法,该方法除不进行VNF聚合外,所有过程皆与本文所提方法保持一致。
3.1 方法评价指标
本文采用请求接受率、平均带宽开销、SFC平均可靠性、SFC平均端到端时延以及长期平均收益开销比来衡量算法的性能。
(1) 请求接受率ωaccept定义为
(24)
式中:NUMsuc(T)表示T时间内成功部署的SFC数目;NUMv(T)表示T时间内到达的SFC请求总数目。
(2) 平均带宽开销Bcost_ave定义为
(25)
式中:Bcostsg是成功部署的SFCg所消耗的带宽。
(3) SFCg的可靠性为
(26)
则SFC的平均可靠性定义为
(27)
(4) SFCg的端到端时延为
(28)
则SFC平均端到端时延定义为
(29)
(5) 在t时刻,成功部署一个SFCg的收益为
(30)
物理网络的资源开销为
(31)
式中:α,β,γ,χ分别表示收益和开销中计算、存储、转发与带宽资源的比重,本文中均设为1。则长期平均收益开销比定义为
(32)
3.2 仿真环境设置
仿真环境中物理网络是由100个节点和525条链路组成的连通图,相当于一个中型网络拓扑,SFC请求服从到达率λ=0.05的泊松分布,生存时间服从μ=1 000的指数分布,仿真时间为50 000个单位。其余各项参数如表1所示。
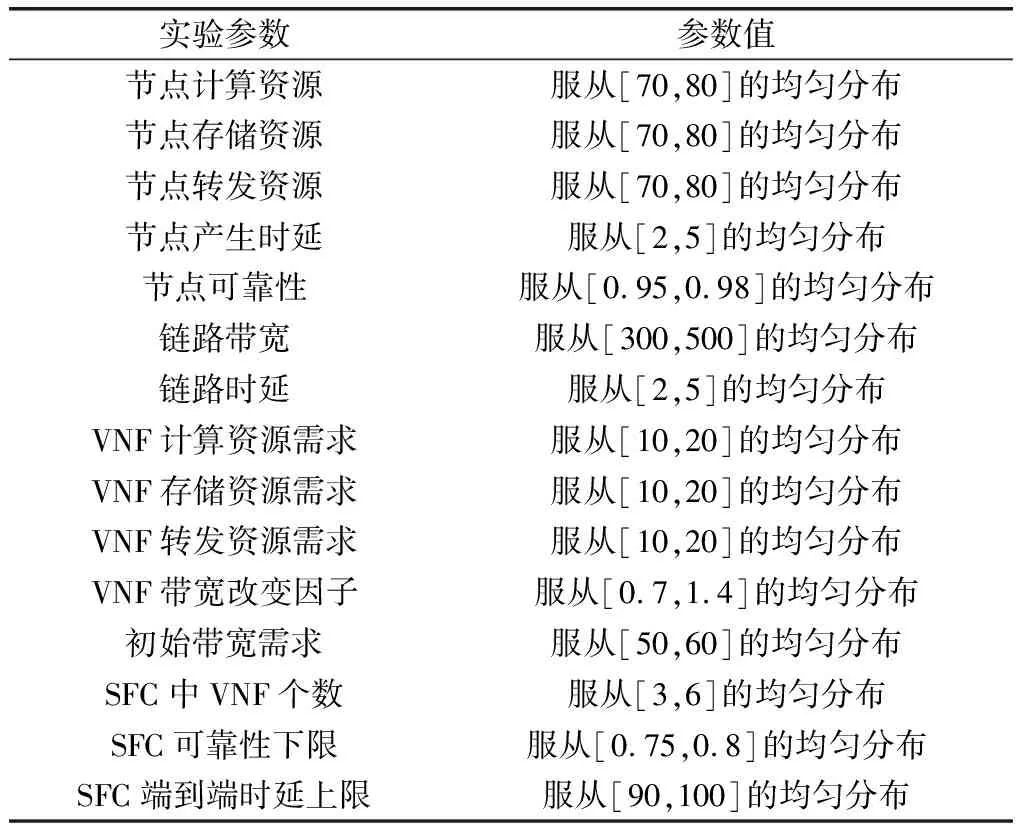
表1 仿真参数Table 1 Simulation parameters
3.3 实验结果分析
为避免随机因素影响,仿真实验共进行10次,取每次结果的平均值作为最终的实验结果,如图3~图8所示。
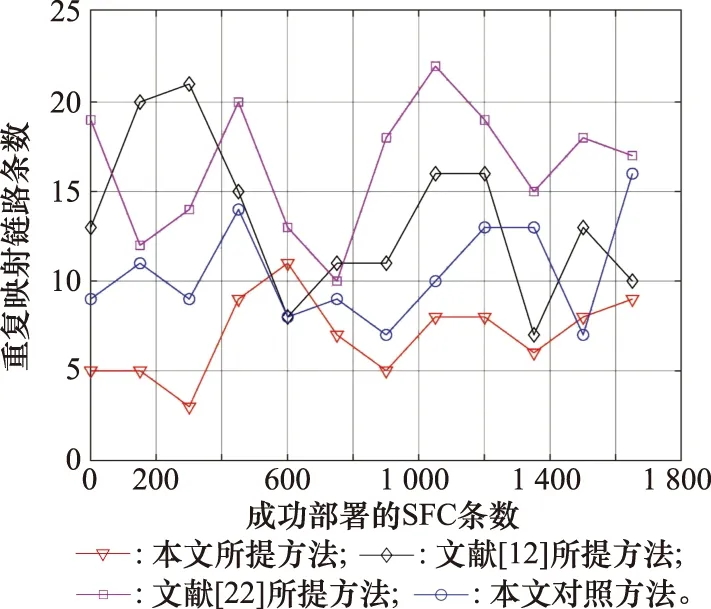
图3 重复映射链路条数Fig.3 Number of links that are mapped repeatedly
从图3可以发现,本文所提方法与对照方法的链路重复映射条数小于另外两种方法,即乒乓效应低于另外两种方法。这是因为在部署过程中这两种方法进了链路约束,有效降低了同一条SFC上的不同虚拟链路映射到相同物理链路上。而另外两种方法未考虑乒乓效应,所以链路重复映射条数较高。
从图4可以发现,本文所提方法的收益开销比保持在0.75以上,明显优于其他3种方法。这是因为本文所提方法根据带宽需求变化对VNF进行聚合处理,并且在部署时利用链路约束降低了乒乓效应,有效降低了带宽开销,从而提升了长期平均收益开销比。本文对照方法未进行VNF聚合,但在部署时利用链路约束降低了乒乓效应,所以其长期收益开销比大于另外两种方法。文献[12]和文献[22]所提方法未进行VNF聚合,也未考虑乒乓效应,所以长期收益开销比较低。
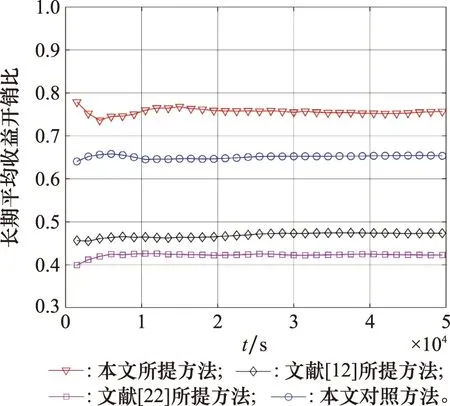
图4 长期平均收益开销比Fig.4 Long-term average revenue overhead ratio
从图5可以发现,本文所提方法与对照方法的映射成功率都在0.95以上,优于另外两种方法,这是因为这两种方法在进行部署时考虑了物理节点的综合时延、可靠性以及拓扑属性,使得部署后的SFC能较好地满足时延与可靠性约束,所以映射成功功率较高。而文献[12]所提方法未考虑链路的时延,文献[22]所提方法对节点和链路的时延均未作考虑,使得部署后的SFC未能很好满足时延约束,所以映射成功率较低。

图5 映射成功率Fig.5 Mapping success rate
从图6可以发现,本文所提方法的SFC平均可靠性最高,保持在0.91以上,这是因为进行了VNF聚合后,多个VNF部署到同一个物理节点上,并采用离差最大化的多指标决策方法赋予对排序作用大的评价指标更高权重,有效地提高了SFC的可靠性。文献[22]所提方法的SFC平均可靠性保持在0.9以上,仅次于本文所提方法,这是因为该方法在第一阶段将VNF都部署在可靠性最高的物理节点上,后两个阶段只是在此基础上作调整,所以能保持较高的可靠性。本文对照方法在部署阶段考虑了拓扑属性、节点综合时延与可靠性,文献[12]所提方法考虑了拓扑属性与节点可靠性,均未对VNF进行聚合,所以其SFC可靠性较低,但由于本文对照方法采用离差最大化多指标决策方法,所以在可靠性方面还有一定优势。

图6 SFC平均可靠性Fig.6 Average reliability of SFC
从图7可以发现,本文所提方法与对照方法的SFC平均端到端时延低于另外两种方法,分别保持在45 ms和50 ms左右,这是因为这两种方法在部署阶段既把物理节点综合时延作为评价指标,还利用链路约束降低了乒乓效应,所以能获得更低的节点与链路时延。而文献[12]所提方法未考虑链路时延,文献[22]所提方法对节点时延与链路时延均未考虑,所以SFC平均端到端时延较高。
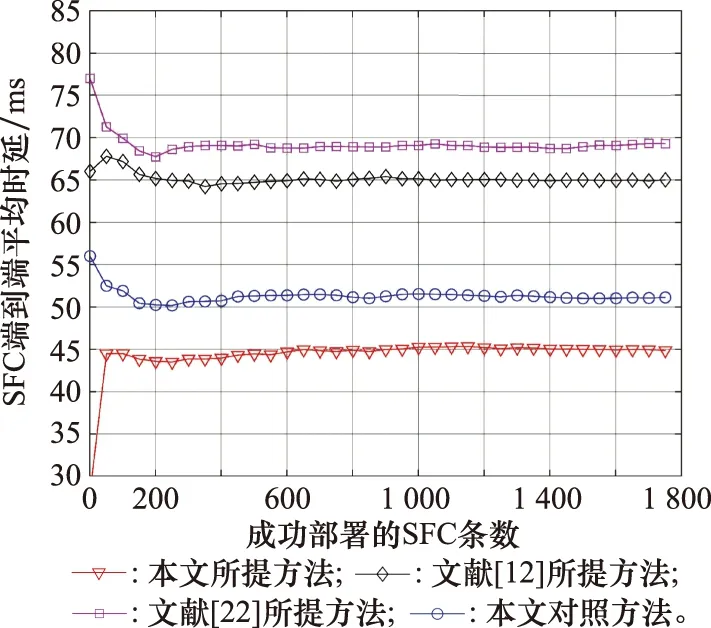
图7 SFC平均端到端时延Fig.7 Average end to end delay of SFC
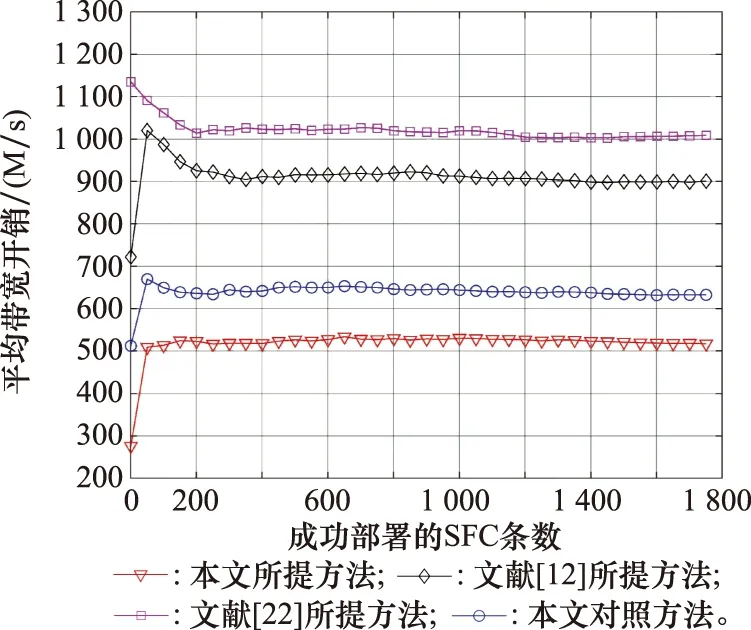
图8 平均带宽开销Fig.8 Average bandwidth overhead
从图8可以发现,本文所提方法的带宽开销低于另外3种方法,保持在500 M/s左右,这是因为本文所提方法既根据带宽需求对VNF进行了聚合处理,在部署时还利用链路约束降低了乒乓效应,所以获得了较低的带宽开销。而本文对照算法未进行VNF聚合处理,但降低了乒乓效应,所以带宽开销仅高于本文所提方法。另外两种方法未进行VNF聚合,也未考虑乒乓效应,所以平均带宽开销较高。
4 结 论
针对NFV环境中服务功能链的部署问题,本文提出一种基于流量优化的可靠服务功能链部署方法。首先根据虚拟链路的带宽需求变化对VNF进行聚合处理,使大带宽虚拟链路上的流量变为服务器的内部流量,有效降低了带宽开销,提升了收益开销比。然后综合考虑节点可靠性、综合时延以及拓扑属性,使用离差最大化的多指标决策算法对满足聚合后VNF资源需求的物理节点进行评价,并利用链路约束降低乒乓效应,依次将VNF部署到评价度最高的节点上。最后采用k-最短路径算法完成虚拟链路的部署。实验表明,该方法在保证SFC可靠性的基础上,对长期平均收益开销比、映射成功率、端到端时延以及平均带宽开销有较大优化。下一步将对流量预测进行研究,进一步提高NFV环境中网络的性能。
