基于CRC的ASM信号维特比纠错算法

张培欣, 王建新, *, 任 鹏, 杨树树, 宋海伟

(1. 南京理工大学电子工程与光电技术学院, 江苏 南京 210094; 2. 南京电子设备研究所, 江苏 南京 210007)

0 引 言

船舶自动识别系统(automatic identification system, AIS)是一种广为人知且被广泛使用的船舶自动追踪系统[1-4],该系统由国际海事组织(international maritime organization, IMO)、国际航标协会(international association of marine aids to navigation and lighthouse authorities, IALA)等国际有关组织于20世纪90年代提出[5-7]。随着国际海事贸易的日渐繁盛,海上航行安全、海事态势感知、港口安全等需求也与日俱增,AIS早已不堪重负。因此,甚高频数据交换系统(very high frequency data exchange system, VDES)应运而生[8-12]。VDES整合了甚高频数据交换(very high frequency data exchange, VDE)、应用特定消息(application-specific messages, ASM)以及AIS,特有的功能及技术参数,并且根据各种使用场景又细分为多种格式。

ASM主要被用于船与船、船与岸基站、船与卫星之间传递特定的应用消息[13]。根据ITU与IALA共同起草的建议书[14-15],ASM被划分为10种格式,分别用链路配置编号1～10表示,其中4～10号采用了Turbo编码,而1～3号没有。众所周知,Turbo编码是一种能显著提升信道容量的前向纠错(forward error correction,FEC)编码方式[16-20],这使得采用了Turbo编码的4～10号ASM信号即使在较低信噪比(signal to noise ratio, SNR)下也有不错的解码性能,而没有采用Turbo编码的1～3号ASM信号的解码性能则相对较差。本文利用ASM信号中同样具有冗余信息的循环冗余校验(cyclic redundancy check, CRC)字段纠错,从而提高1～3号ASM信号的解码性能。

传统的基于CRC的纠错算法主要有两种:一种是查表式CRC纠错算法[21],另一种是基于CRC的维特比纠错算法[22-24]。顾名思义,查表式CRC纠错方法首先需要一张表,这张表是根据参与CRC运算的信息比特长度以及CRC多项式生成的。当接收到的比特信息无法通过CRC时,就把接收到的信息比特按制表规则做相同运算,若在表中查到运算结果,则可根据查到的位置确定出错比特位置。最简单的查表式CRC纠错算法仅能纠正1 bit错误,也有学者开发出了能纠正2 bits错误的查表式CRC纠错算法[25],结合置信度判定,更是能实现多比特纠错[26]。查表式CRC纠错算法对解调性能确实有所提高,但提高幅度有限。相比于查表式CRC纠错算法,基于CRC的维特比纠错算法能纠正的错误比特数并不受限制,因此其纠错性能要比查表式CRC纠错算法优异。基于CRC的维特比纠错算法是在维特比解码的过程中,让CRC寄存器状态也参与路径转移,最后在所有能通过CRC的路径中,挑选与接收信号相关程度最大的路径做后续解码。基于CRC的维特比纠错算法的缺点也很明显,即计算量太大。其性能严重依赖于路径的数目,因为路径数目越多,尝试的可能性越多,越有可能找到正确的结果。也有一些文章尝试降低其计算量,例如符号状态数减少的维特比算法[27-28],以及部分CRC辅助纠错算法[29]。然而这些算法都需要在性能与计算量之间取舍。除了计算量太大这一问题以外,传统维特比算法及其改进算法的分支度量设计过于理想化,其导致的性能损失也是不容忽视的一个问题。

为提高1～3号ASM信号的解码性能,本文综合了符号状态数减少的维特比算法和部分CRC辅助纠错算法,在尽量减少牺牲性能的前提下降低了计算量。同时,为了解决传统分支度量计算公式的设计缺陷导致的性能下降,重新设计了路径度量,并基于此推导出了新的分支度量。仿真表明,新的分支度量解决了传统分支度量设计过于理想化导致的性能损失;使用12个CRC移位寄存器参与纠错能够实现1 dB的误帧率(packet error rate,PER)性能提升;同时,采用合理的符号状态数降低策略,能在几乎不损失性能的前提下进一步将计算量降低3/4。

1 应用特定消息

根据ITU与IALA共同起草的建议书[14-15],ASM根据应用场景的不同又分为两大类:岸基ASM(terrestrial component of ASM,ASM-TER)和星载ASM(satellite component of ASM,ASM-SAT)。本文研究的1～3号ASM属于ASM-TER,因此,本文所有内容也都基于ASM-TER。ASM-TER帧格式如图1所示。

图1 ASM-TER帧格式Fig.1 ASM-TER frame format

本文的重点是解码,因此图1中其他部分在此不多作介绍,只重点介绍信息序列。信息序列是整个数据帧中真正待传输的数据,但它并非是由待传输的原始二进制信息直接填充而来,而是要经过补零、CRC、FEC、比特加扰等一系列操作后得到的。根据标准,CRC采用32 bit的ITU-T V.42 {RD-5}计算(生成多项式以16进制表示为0x04C11DB7,移位寄存器初始状态为全1);1～3号ASM信号的FEC倍率为1,即不使用FEC,所以在此不多作介绍;比特加扰多项式表示为F(x)=1+x-14+x-15,初始状态设定为100 101 010 000 000。

生成ASM-TER帧后,按照标准,还要将帧按照π/4四相相移键控(quadrature phase shift keying,QPSK)方式映射。实际中,接收端一般会将π/4 QPSK信号调整成QPSK信号以便于解调,对于ASM-TER信号,只要将相角为π/2整数倍的符号逆时针旋转π/4即可。

rn=sn(α)+wn

(1)

式中:wn是复高斯白噪声,其分布服从N(0,γN)(γN表示噪声功率)。

2 传统基于CRC的维特比纠错算法

本文提出的算法是在传统基于CRC的维特比纠错算法基础上改进实现的。维特比算法是由Viterbi于1967年提出的一种可用于任何符号序列的最大似然判决器[30-31]。其基本思想是构造马尔可夫链,然后在所有的可能路径中,找出可能性最大的路径,其对应的符号序列即最终的解码结果。为直观理解维特比算法的思路和过程,下面以QPSK信号为例介绍维特比算法。

2.1 维特比算法

根据文献[16]所述,对α的最优非相干估计可表示为

(2)

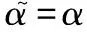
(3)

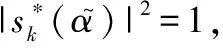
(4)

式(4)的每次计算都需要将n时刻之前的接收信号和假设信号进行相乘累加,浪费了巨大的计算量。同时可以观察到,当前时刻的路径度量与下一时刻的路径度量存在简单的数学关系:

(5)

因此,路径度量可以迭代计算而不用每次重新计算。代表相邻时刻路径度量之间迭代关系的式被定义为分支度量。为了限制计算量,可以仅使用当前时刻附近NT个符号计算分支度量(NT被称之为记忆长度):

(6)

同时可以用n时刻前NT-1个符号定义当前的符号状态:

(7)

基于式(7)对于符号状态的定义,式(6)可改写为

(8)

(9)

有了转移路径度量和分支度量的计算公式,只需要在每个时刻将所有的可能转移情况代入公式,计算出对应的分支度量和转移路径度量即可;对于下一时刻的每个状态,在所有转移到当前符号状态的分支中,挑选转移路径度量最大的作为幸存路径,同时将其转移路径度量作为自己的路径度量,并记录下路径信息;最后,挑选路径度量最大的一支,根据记录的路径信息依次前推,根据符号状态与码元的对应关系查找码元即可实现回溯解调。为了方便查询,将所有可能的符号状态列出即可得到符号状态表。同理,将所有可能的转移情况列出可构成符号状态转移表。符号状态表用于最后根据符号状态查询对应的码元从而实现解调,符号状态转移表用于转移过程中查询可能的转移过程。

2.2 基于CRC的维特比纠错算法

维特比算法的思路是尝试多种可能的码序列,从中找出可能性最大的作为解码结果。尝试的组合越多,可能得到正确的结果的可能性越大,这种思路适合用于纠错。一种简单的思想[22]就是,将CRC移位寄存器中的值也作为状态的一部分,参与路径的转移。这种方法就要求在每个分支计算分支度量和路径度量的同时,也计算该分支对应的CRC校验码。直到最后,在所有能通过CRC的路径中,挑选可能性最大的一支作为解码结果。

需要注意的是,由于标准中规定经过CRC后的序列还需经过比特加扰,因此在对接收信号进行纠错解码之前,要先进行解扰。由于加扰操作实际上等同于将原序列与一特定伪随机序列进行模二加,因此只要将接收信号与同一伪随机序列进行一次模二加即可实现解扰。

当接收信号出现少量错误时,由于传统维特比算法是寻找与接收信号相关性最大(传统算法中体现为路径度量最大)的路径,所以也只能解出与接收信号匹配的错误序列(对应路径记为路径1)。而在基于CRC的维特比纠错算法中,虽然路径1依然是路径度量最大的,但它并不能通过CRC。而在路径1附近的其他路径,就有可能刚好尝试了正确的符号组合(记为路径2)。虽然路径2的路径度量不是最大的,但由于其与路径1的差别很小,所以其路径度量也只会比路径1的略小。同时由于CRC的随机性,其他能通过CRC的路径与接收信号的相关性通常不会很大,对应的路径度量也不大。因此,只要在最后所有能通过CRC的路径中,挑选相关性最大的一支解码,即可实现纠错。

在基于CRC的维特比纠错算法中,由于CRC移位寄存器中的值也参与了路径转移,路径的状态也不仅仅由符号状态决定,而是由符号状态和CRC状态共同决定,因此,定义扩展状态

(10)

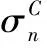
对于n+1时刻的每个扩展状态,都有可能由多条不同的路径转移而来。因此,对于n+1时刻的每个扩展状态,要从所有的可能转移路径中选取对应转移路径度量最大的作为幸存路径,同时将其转移路径度量作为自己的路径度量,并记录下路径信息。以此类推,直到结束。最后,挑选能通过CRC的路径中路径度量最大的一支,根据记录的路径信息依次从后往前,根据符号状态表查找码元即可实现回溯解调。

3 改进的基于CRC的维特比纠错算法

传统的基于CRC的维特比纠错算法虽然性能出色,但也有其弊端。以本文的应用场景为例,假设NT=3,则符号状态数NS=4NT-1=16,CRC状态数NCRC=232≈4.295×109,总的扩展状态数达到了惊人的6.872×1010,这显然是不可接受的。为此,需要降低扩展状态的数量。本文提出的算法通过两个方面降低扩展状态数:降低符号状态数和降低CRC状态数。

除了计算量巨大这一问题之外,传统基于CRC的维特比纠错算法还有一个不容忽视的问题,即由分支度量计算公式的设计缺陷导致的性能损失。为解决这一问题,重新设计了新的路径度量计算公式,并在此基础上推导出了新的分支度量计算公式,弥补了传统算法的性能损失。

3.1 符号状态数降低

符号状态数的大小由记忆长度NT和每个符号的可能状态数M决定,NS=MNT-1。因此,要想降低符号状态数NS,要么降低M,要么降低NT,或者两者同时降低。

降低NT是直接以性能损失为代价的。这是因为维特比算法的一个特点就是尝试的可能路径越多,解码正确的可能性越大,而NT直接决定了路径数量。因此,降低NT的方法不做考虑。

(11)

为了保证状态转移的唯一性,分组方式需要满足两个要求:

(1) 集合的数量Jk应当是非增长的(J1≥J2≥…≥JK);

(2) 前一时刻的任一集合应当是下一时刻中某个集合的子集。

J=[J1,J2,…,JK]

(12)

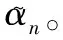
经过上述操作,每个符号的可能状态数不再是M而是Jk,此时的符号状态数应当是Jk的乘积,即

(13)

只要不是所有的Jk都等于M,那么符号状态数就得到了降低。具体使用的时候,符号状态表和符号状态转移表也要根据分组方式构建。

3.2 CRC状态数降低

传统的基于CRC的维特比纠错算法需要将所有CRC移位寄存器状态全部用于纠错,这就导致了扩展状态数急剧增大。以本文应用场景为例,ASM-TER采用的是32位CRC,就算仅用两个符号表示符号状态,扩展状态数也达到了惊人的109量级,并且CRC在这之中做出了极大的贡献。很自然的就能想到,削减CRC参与纠错的长度就能有效地以指数次幂减少扩展状态数。

CRC状态的本质就是CRC移位寄存器中的值,可以将其进行拆分[29]：

(14)

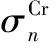
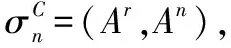
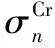
3.3 新分支度量设计

除了巨大的计算量,传统的基于CRC的维特比纠错算法还有另外一个问题,即由于其分支度量计算公式的设计过于理想化导致的性能损失。下面将结合实例阐述这一问题。

为便于阐述,首先对式定义的分支度量进行改写

(15)

要解决这一问题,只能重新设计路径度量,并基于此推导新的分支度量。现在让我们重新回顾维特比算法的基本思想:寻找可能性最大的路径。式及其后续的简化变形都是用接收信号与假设信号之间的相关性衡量可能性,相关性越大则可能性越大。但是衡量可能性的方式不只相关性这一种,接收信号与假设信号之间的误差也能用于衡量可能性,误差越小可能性越大。因此,本文重新定义的路径度量表示为

(16)

基于式(16)的分支度量可表示为

(17)

同样为了限制存储空间和计算量,仅使用当前时刻附近NT个符号计算分支度量:

(18)

此时,对α的估计为

(19)

至此,我们完成了新路径度量的设计和新分支度量的推导。本文提出的算法步骤总结如下。

步骤 1状态表构建:根据需求选取合适的分组方式和参与纠错的CRC寄存器位数,并据此构建符号状态表、符号状态转移表。

步骤 2初始化:构建路径信息表与路径度量表。路径信息表用于记录转移到当前符号状态之前的有用信息,路径度量表用于记录当前状态的路径度量。路径度量表中,对应CRC移位寄存器数值为全1的应初始化为0,其他全部初始化为正无穷。

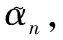
步骤 4状态转移:根据上步幸存的分支度量计算转移路径度量,同时计算CRC移位寄存器在转移后的状态。

步骤 5路径幸存:在n+1时刻,每个扩展状态都有多种可能的转入路径,选取其中转移路径度量最小的一条作为幸存路径,并把其转移路径度量作为当前扩展状态的路径度量,同时记录下路径信息。

步骤 6回溯解调:当算法运行至最后一个时刻,只保留对应CRC状态为全0的路径,选取其中路径度量最小的一个,并根据记录的路径信息逐步回溯解调。

4 性能仿真

采用1号ASM-TER信号进行仿真,符号速率Rs=9 600 ksps,假设接收信号中无频偏、相偏,蒙特卡罗仿真1 000次,使用PER衡量各算法的性能。

4.1 基于新分支度量的维特比算法性能

为考察新分支度量对性能的影响,本仿真中所有算法均不包含纠错功能且不降低符号状态数。基于新分支度量的维特比算法性能如图2所示。

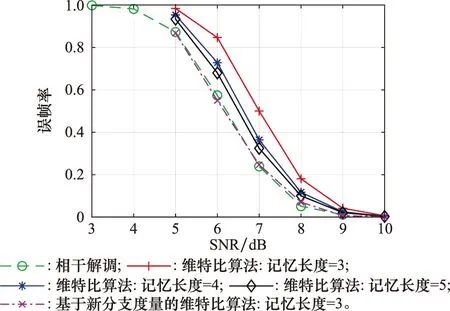
图2 基于新分支度量的维特比算法性能Fig.2 Performance of the new branch metric based Viterbi algorithm

图2中SNR表示每比特能量比上噪声功率谱密度(Eb/N0)。从图2中可以看出,以PER=0.8为基准,记忆长度NT=3时的传统维特比算法与相干解调有着约1 dB不到的性能差距,随着NT的增加,性能差距逐渐缩小,但直到NT=5时依然有约0.3 dB的性能损失。同时从图2中也可以看到,基于本文提出的新分支度量的维特比算法在NT=3时的性能就几乎与相干解调算法重合。这充分说明了本文提出的新分支度量的有效性。

4.2 改进的基于CRC的维特比纠错算法在不同CRC状态数降低策略下的性能

本小节仿真了改进的基于CRC的维特比纠错算法在不同CRC状态数降低策略下的性能,本节中统一NT=3且不降低符号状态数,具体性能如图3所示。从图3中可以看到,以PER=0.8为基准,对于改进的基于CRC的维特比纠错算法,只用4个CRC寄存器参与纠错相比于相干解调算法几乎没有性能提升;当参与纠错的CRC寄存器个数提高到8时,性能有了约0.3 dB的提升;而当使用12个CRC寄存器参与纠错时,性能提升了约1 dB。图3说明,使用部分CRC参与纠错能获得一定的性能提升。

图3 本文提出算法在不同CRC寄存器个数下的性能Fig.3 Performance of the proposed algorithm with different number of CRC registers

4.3 改进的基于CRC的维特比纠错算法在不同符号状态数降低策略下的性能

本节仿真了改进的基于CRC的维特比纠错算法在不同符号状态数降低策略下的性能,本节中统一设定NT=3,参与纠错的CRC寄存器位数NCr=12。具体性能如图4所示。

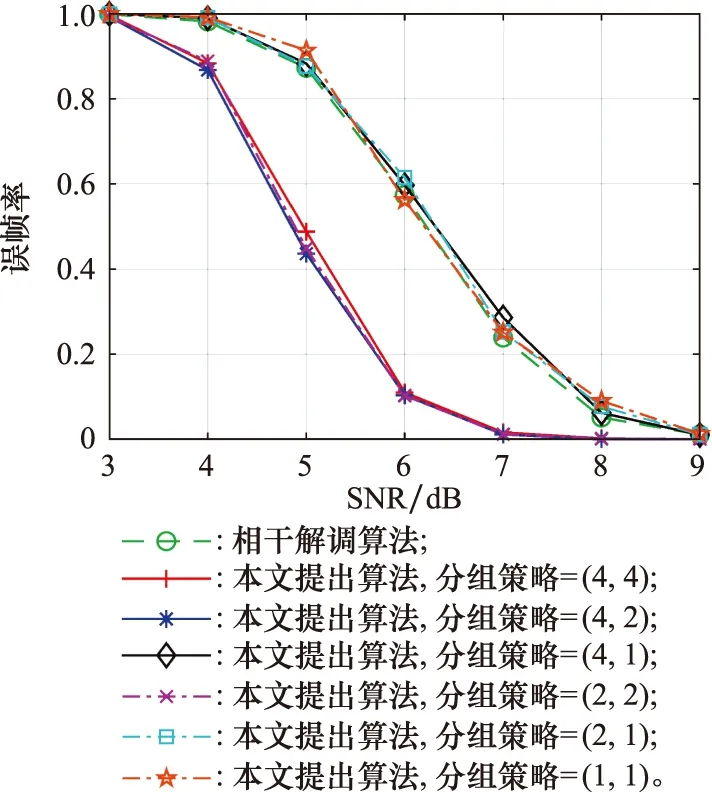
图4 本文提出算法在不同符号状态数降低策略下的性能Fig.4 Performance of the proposed algorithm with different strategy of reducing the number of symbol statuses

从图4中可以看到,在使用12位CRC寄存器参与纠错的情况下,J=(4,4)、J=(4,2)以及J=(2,2)时PER性能几乎相同,相较其他情况性能最好。同时,J=(4,1)、J=(2,1)、J=(1,1)时PER性能有较大损失,其性能与相干解调算法几乎相同。同时从图4中也可以看到,虽然J=(4,1)、J=(2,2)两种策略下分支数量相同,但J=(4,1)时的PER性能却更差,很显然这是由于符号分组策略跳跃过大造成的。图4说明,降低符号状态数能在有效降低计算量的同时做到几乎不损失性能。但符号状态数也不能无限制降低,以本文应用场景来说,综合权衡性能与计算量,最合适的符号状态数降低策略为J=(2,2)。

5 结 论

为提高1～3号ASM信号的解码性能,本文提出了一种基于CRC的改进维特比纠错算法。为解决基于CRC的维特比纠错算法计算量太大的问题,本文从两个方面减少了算法的路径数从而减小计算量:一方面是通过将符号的可能状态分组以降低符号状态数,同时详细阐述了分组的基本要求和最佳分组方式;另一方面是通过削减CRC参与纠错的长度减少CRC状态数,从而减少扩展状态数。除了减少计算量,本文还详细分析了传统维特比算法分支度量的设计缺陷导致的性能损失。为解决这一问题,基于维特比算法寻找可能性最大的路径的思想,本文重新推导了一个新的分支度量。仿真表明,在其他条件相同的情况下,新分支度量解决了传统分支度量导致的性能损失问题,在仅用两个符号定义符号状态的情况下就几乎与相干解调算法的性能一致。仿真还表明,对于ASM-TER信号,用8个CRC寄存器参与纠错,就能将误帧率性能相对于相干解调提升0.3 dB,用12个能提升1 dB。通过仿真发现,对于ASM-TER信号来说,最佳的符号状态数降低策略为J=(2,2),该策略在几乎不降低解码性能的同时,计算量仅为J=(4,4)完全不分组策略计算量的1/4。