可重构智能面辅助的低精度量化大规模MIMO系统的信道估计
2021-11-11李彬睿张忠培
李彬睿, 张忠培
(电子科技大学通信抗干扰国家级重点实验室, 四川 成都 611731)
0 引 言
大规模多输入多输出(multiple input multiple output,MIMO)是5G通信系统的核心候选技术之一[1]。可重构智能面(reconfigurable intelligent surface,RIS)作为最近新出现的技术,被认为具有巨大潜力,能以低成本的方式高效地提升大规模MIMO系统的性能[2]。RIS由可重构的无源反射天线组成,这些天线是由新开发的信息超材料制成的[3-5]。与传统的只有固定移相器的反射面不同,RIS的各个元件通过智能微控制器的控制,可以独立地对入射信号的相位偏移进行配置后,再反射出去[3-5]。
大规模MIMO系统的信道估计深受学术界和工业界研究人员的重视[6-9]。为降低估计该系统的大维度信道时所需要的导频开销,文献[6]将大规模MIMO系统的信道估计问题建模为低秩矩阵近似问题,然后利用压缩感知算法恢复了信道信息。其所推荐的算法估计性能优于传统的最小二乘法(least squares,LS)信道估计算法。文献[7]将系统上行信道建模为块稀疏信号,并提出块压缩感知算法对信道进行了稀疏恢复。其所提出的块压缩感知算法相较传统压缩感知算法,能够更准确地恢复出目标信号。在多用户场景中,文献[8]指出在地理位置上相近用户的信道矩阵存在着公共支撑集,并提出联合正交匹配追踪(joint orthogonal matching pursuit,JOMP)信道估计算法以先联合估计公共支撑集再恢复剩余支撑集。相比于各用户单独恢复信道信息,JOMP算法能够更有效地恢复信道信息。基于宽带大规模MIMO系统中不同子载波的子信道之间的共同稀疏性,文献[9]提出了一种分布式稀疏度自适应匹配追踪(distributed sparsity adaptive matching pursuit,DSAMP)信道估计算法,提升了对这种共同稀疏结构信号的恢复性能。文献[10]提出基于最近邻学习(nearest neighbor learning,NNL)算法的近似消息传递算法利用系统提供的外信息提升信道估计性能。
但是由于RIS没有信号处理能力,因此RIS辅助大规模MIMO系统的信道状态信息的获取更具有挑战性。最近有许多研究者开始关注到该信道估计问题[11-19]。文献[11-12]提出了一种基于开/关的估计方法,通过依次开关RIS各元件以获取各元件单独工作下信道的观测值,最后采用LS估计算法完成信道估计。在文献[13-14]中,对基站(base station,BS)-RIS-用户(user equipment,UE)的级联信道采用两阶段算法进行估计,既第一步估计BS-RIS信道,第二步完成RIS-UE信道估计。文献[15-16]提出了有效信道估计来代替级联信道估计问题,然后利用传统压缩感知算法正交匹配追踪(orthogonal matching pursuit,OMP)算法完成信道估计。文献[17]在多用户场景中利用平行因子(parallel factor,PARAFAC)分解算法对所有用户的信道组成的信道张量进行了估计。文献[18-19]利用多用户的有效信道之间存在的公共支撑集和行稀疏特性,提出了双稀疏OMP算法提升信道估计性能。
然而,之前的文献都是假设接收端的观测值是由高精度模数转换器(analog-to-digital converter,ADC)量化的,比如长期演进(long term evolution,LTE)和LTE增强(LTE-advanced,LTE-A)标准中规定的16位量化或者理想量化,但这会导致大规模MIMO系统的高硬件成本和功耗增加[20-22]。在实际的大规模MIMO系统中,采用经济、环保的低精度ADC对观测数据进行量化以克服硬件成本高和功耗增加的问题,但这给信道估计带来了更大的挑战[23-28]。文献[23-28]中的大部分相关研究都是集中在没有RIS辅助下的低精度量化大规模MIMO系统中,利用压缩感知技术获取信道状态信息。文献[23-24]中分别提出基于迭代硬阈值算法和凸优化算法的低精度量化系统的信道估计方法。文献[25-26]中,提出了双线性广义近似消息传递算法来联合进行信道估计和数据检测。文献[27]提出了基于期望最大化(expectation maximization,EM)的近似消息传递(generalized approximate message passing,GAMP)算法和基于EM算法的矢量近似消息传递算法来解决毫米波大规模MIMO中的宽带信道估计问题。文献[28]对RIS辅助的低精度量化大规模MIMO系统性能进行了研究,同时考虑了RIS中的相位噪声在此系统中的影响。但是RIS辅助的低精度量化的大规模MIMO系统的信道估计问题至今仍未有相关的文献报到过。鉴于此,本文主要研究RIS辅助低精度量化的大规模MIMO系统的信道估计问题。
本文基于可重构智能面辅助的低精度量化大规模MIMO系统的级联信道推导出等效信道,并利用等效信道在虚拟角域的稀疏结构结合EM-GAMP算法和NNL算法更新先验分布参数提出EM-NNL-GAMP算法。仿真结果表明该算法可有效提升信道估计性能。
1 系统模型
在本文讨论的RIS辅助的大规模MIMO系统中,RIS被部署在BS和单天线UE之间以辅助两者间的通信,如图1所示。RIS由N个反射元件组成,BS配备有M根天线。本文中忽略了BS和UE之间的直接链路的信道估计问题。因为该问题可以通过关闭所有RIS的元件,然后使用传统的大规模MIMO信道估计方法来解决[13]。

图1 可重构智能面辅助低精度大MIMO系统结构Fig.1 Architecture of reconfigurable intelligent plane aided low precision large MIMO system
同时,在直接链路的信道被估计出后,就可以在估计反射链路时,将直接链路在信道模型中的影响消除掉。因此,反射链路信道E(t)可以被建模为级联信道,并且表示为
E(t)=GS(t)f
(1)
式中:G∈CM×N和f∈CN分别表示BS-RIS信道和RIS-UE信道。而S(t)被定义为diag(s(t)),即S(t)是一个以s(t)的元素为对角元素的对角矩阵。其中s(t)是RIS的相移向量可以被表示为
s(t)=[s1,tejξ1,t,s2.tejξ2,t,…,sN,tejξN,t]T
(2)
式中:sn,t∈{0,1}和ξn,t∈[0,2π]分别表示在第t时刻RIS的第n个无源元件的开/关状态和相移配置。根据文献[11-14],想要完全估计出级联信道,必须独立估计出G和f。这类信道估计算法的复杂度往往很高,而且由于信道测量值中两者总是以乘积的形式结合在一起的,故而估计出的G和f间会存在一定的模糊性[13]。对于上行链路传输,BS在第t时刻收到的信号[15-16]可以表示为
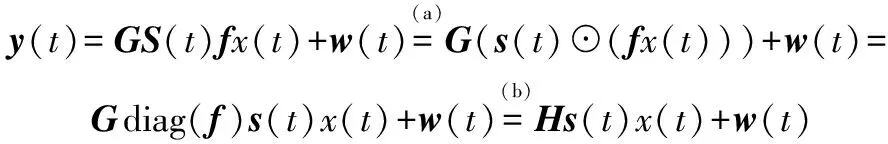
(3)
式中:⊙表示hadamard积,既向量元素相乘运算符,x(t)∈C和w(t)~CN(0,σ2I)分别表示第t时刻的传输符号与加性高斯白噪声(additive white Gaussian noise,AWGN)。式(3)中的步骤(a)是利用S(t)构建一个对角矩阵,步骤(b)中定义了有效信道H=G⊙diag(h)。根据式(3),有效信道H的信息足以完成联合主被动波束形成[16]。因此,信道估计问题的目标变为基于观测值y(t),已知的导频符号x(t)和RIS的相移向量来估计有效信道矩阵H。
在实际的大规模MIMO系统中,为了降低硬件成本和功耗,系统采用低精度ADC对接收信号进行量化。上行接收信号y(t)中的各元素首先通过缩放矩阵进行缩放,以便信号在输入ADC之前信号各元素的振幅能够以高概率被缩放到[-1,1]范围之内。根据文献[29]中提出的三西格玛规则,每个天线的标度因子ηm可以表示为
(4)
式中:hm表示H的第m行。然后缩放后信号可以表示为
(5)
式中:Ω=diag([η1,η2,…,ηM])。各天线上接收的信号经过缩放后,再由安装在后端的ADC对其实部和虚部分别地完成采样量化。于是得到量化后接收信号:

(6)


表1 不同量化比特数对应Δnorm值[29]Table 1 Corresponding Δnorm values of different quantization bits
2 信道模型
在本节中,BS-RIS信道G和RIS-UE信道f分别采用窄带几何信道模型(簇模型)。因此,BS-RIS信道模型[9-10]可以表示为
(7)

假设BS和RIS均配备的是均匀面阵(uniform planar array,UPA)。在UPA上分别沿x轴的和y轴等间距分布若干天线单元,各天线单元的位置可以根据其在x轴和y轴的坐标来描述。因此,BS的天线阵列响应向量可以写成
(8)

通过类似方式,RIS-UE信道f可以建模为
(9)
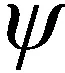
(10)
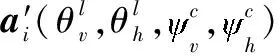
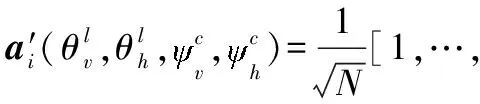
(11)
(12)
式中:
(13)
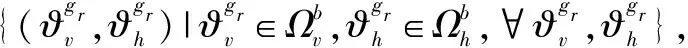
(14)

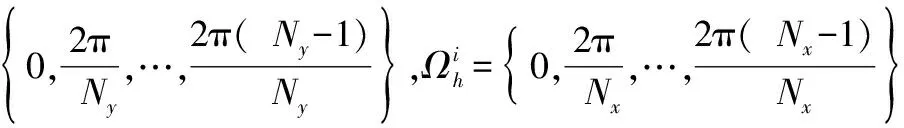
BS和RIS通常被部署在比较高的建筑物上以实现对广阔区域的覆盖。根据文献[9,15,18-19]这种场景下,BS和RIS周围只有有限的散射体。这造成在BS-RIS信道和RIS-UE信道都只在少数特定AoA和AoD的路径是有效路径,也即是说Ha的元素在少数列/行向量中是非零的,这种特殊的稀疏结构在文献[15]和文献[18-19]中被称为行-列块稀疏,如图2所示。
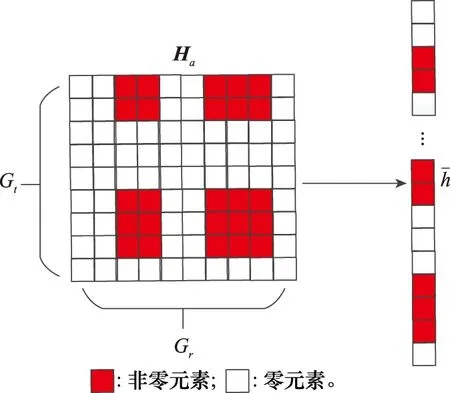
图2 有效信道虚拟角域表示的典型结构及其矢量化示例Fig.2 Typical structure of virtual angular domain representation of effective channel and its vectorization example
3 问题形式
在信道训练过程中,假设导频信号为1,即x(t)=1,∀t。然后通过将所有接收到的信号y(t)写作矩阵形式,式(1)可以重新表示为
(15)
式中:T是导频长;S[s(1),s(2),…,s(T)]∈CN×T和W[w(1),w(2),…,w(T)]∈CM×T。然后利用公式vec(ABC)=(CT⊗A)vecB将式(15)改写为
(16)

(17)
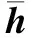
4 信道估计算法设计
(18)

(19)
式中:β[β1,β2,…,βD]T。而量化后接收信号量化后信号的分布可以表示为
(20)
(21)
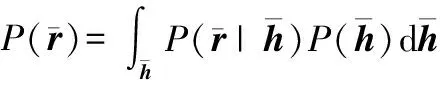

算法 1 EM-NNL-GAMP信道估计算法输入:r,导频Ψ输出:^h初始化:∀k,d:^h1d=0,vh(1)d=1,^s0k=0,λ1=0.1,β1d=0,i=1,ζ循环:∥E-步∀k:vp(i)k=∑dvh(i)d|Ψk,d|2∀k:pik=∑d^hidΨk,d=-^si-1kvp(i)k∀k:利用式(22)或式(24)计算^sik和vs(i)k∀d:vq(i)d=(∑MTk=1|Ψk,d|2vs(i)k)-1∀d:^qid=^hid+vq(i)d∑MTk=1Ψ∗k,d^sik∀d:利用式(27)更新^ui+1d和vu(i+1)d∀d:根据NNL算法,利用式(29)和式(30)更新πid∀d:利用式(31)更新^hi+1d和vh(i+1)d∥M-步利用式(33)更新λi+1∀d:利用式(34)更新βi+1d循环结束条件((∑d|^hi+1d-^hid|2)/∑d|^hi+1d|2<ζ或i>Tmax)
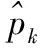
(22)
式中:
(23)
考虑到式(23)中的积分实现起来比较复杂,在实际应用时可以利用加性量化噪声模型(additive quantization noise model, AQNM)进行简化计算,降低计算复杂度[25]。式(23)中积分操作可被简化为
(24)

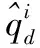
(25)
将式(18)带入式(25),可以变形为
(26)
式中:
(27)
(28)
式中:
(29)
(30)
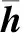
(31)
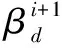
(32)
通过式(32)对λi求导,并令其等于0,可得
(33)
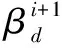
(34)
5 仿真结果
为了探究本文所提算法的性能,在本节中将在不同条件下对算法进行仿真加以验证。BS处采用M=Mx×My=128=16×8规模的UPA。BS和RIS处的UPA都采用半波长间隔,即d=1/2。Ai和Ab分别使用过采样因子ς=2的二维过完备字典矩阵。BS-RIS和RIS-UE信道中的有效路径数为3。信道G和f的竖直AoA、竖直AoD、水平AoA、水平AoD和s中各元素的相位值在0和π之间随机均匀分布。此外,路径增益αl和ρc服从分布CN(0,1)。然后将文献[3-4]中提出的基于开/关方法的LS估计算法和EM-GAMP算法作为基准。算法1最大迭代次数Tmax的值被设定为80。性能比较的度量则采用归一化均方误差(normalized mean square error, NMSE),其定义为
(35)
在图3中,量化比特的数目固定为2,可重构智能面天线采用N=Nx×Ny=32=8×4规模UPA的条件下,即Qbit为2,描绘了关于不同导频长度T和不同信噪比(signal to noise ratio, SNR)下的性能曲线。与同类基准算法的测试结果相比,本文提出的EM-NNL-GAMP算法性能是高于基准算法的性能的。同时根据图3可以观察到,EM-NNL-GAMP算法与基准算法的性能差距随着导频长度的减小而增大。因此,本章所提出的EM-NNL-GAMP算法在导频长度较小的情况下可以体现出更好的性能提升。

图3 在量化比特数为2时不同导频长度和SNR的信道估计性能变化曲线Fig.3 Channel estimation performance curve of different pilot length and SNR under the condition of 2 quantization bits
在图4中绘制了在导频长度固定为48的条件下,即T=48,不同量化比特数目Qbit和不同SNR下的性能曲线。随着量化比特数和SNR的增加,各算法可以获得更好的性能。当SNR小于15 dB时,算法在使用Qbit=3量化与Qbit=2量化时的估计性能几乎相同。因此,本文特别建议系统工作在SNR小于15 dB时采用Qbit=2进行量化。当SNR大于15 dB后,系统使用Qbit=3进行量化更适合。

图4 在导频长度为48条件下不同量化比特数和SNR的信道估计性能变化曲线Fig.4 Channel estimation performance curve of different quantization bits and SNR with pilot length of 48
为了进一步研究系统在采用Qbit=2与Qbit=3量化下的系统性能,本文在图5中绘制了在不同SNR下的系统采用最大比合并(maximal ratio combining,MRC)接收机时的可达速率曲线。其中系统可达速率参考文献[20]中推荐的非理想信道信息下MRC接收机的可达速率表达式计算,而且最佳RIS向量利用文献[16]中推荐的流行优化(manifold optimization,MO)算法计算得到。观测图5可以发现,采用Qbit=3量化,在SNR大于10 dB时,系统可达速率明显优于采用Qbit=2的系统。系统的能量效率分析受限于本文篇幅,将在未来的工作中进行研究。

图5 量化比特数为2和3条件下不同SNR的系统可达速率变化曲线Fig.5 Achievable rate curves of different SNR systems with 2 and 3 quantization bits
在图6中绘制了系统不同RIS天线数下的信道估计性能曲线。系统导频长度被设置为48,SNR被设置为15 dB。随着RIS天线数目的增加,信道估计性能会下降。特别LS算法在RIS数目大于48后,估计性能剧烈下降,这是由于系统信道估计方程组此时陷入欠定状态,而本文提出的EM-NNL-GAMP算法却对此问题不敏感。只是随RIS天线数目增长而估计性能稍微降低。

图6 量化比特数为2和3条件下不同RIS天线数目的信道估计性能变化曲线Fig.6 Channel estimation performance curves of different RIS antenna numbers with quantization bits of 2 and 3

6 结束语
本文针对RIS辅助大容量MIMO系统的信道估计问题,从采用低精度ADC量化的角度出发,提出了一种EM-NNL-GAMP算法来恢复系统的有效信道。仿真结果表明,在相同条件下,与基于开/关的LS算法和传统EM-GAMP算法相比,该算法具有更好的NMSE性能。最后通过仿真结果和讨论,证明了本文提出的算法可以经济、环保地提高系统性能。
