基于回波预处理和相参积累的C&I干扰抑制算法
2021-11-11王国宏孙殿星于亦文张翔宇
张 亮, 王国宏, 孙殿星, 于亦文, 张翔宇
(1. 海军航空大学信息融合研究所, 山东 烟台 264001;2. 中国人民解放军94326部队, 山东 济南 250000;3. 中国电子科技集团仪器仪表有限公司, 山东 青岛 266555)
0 引 言
雷达电子对抗是信息化战争的重要组成部分,强干扰背景下为有效发挥雷达效能,针对特定干扰样式研究相应对抗方法尤为重要[1]。C&I(chopping and interleaving)干扰和频谱弥散(smeared spectrum, SMSP)干扰是Sparrow等人发明的两种针对线性调频(linear frequency modulation, LFM)脉冲压缩雷达的典型干扰样式[2]。区别于全脉冲复制转发密集假目标干扰[3],C&I干扰和SMSP干扰由雷达信号脉内调制生成,单个干扰信号经雷达匹配滤波器即可输出高密度虚假目标群,欺骗兼压制雷达系统。不同于SMSP干扰,C&I干扰子信号调频斜率与雷达发射信号调频斜率相同,SMSP干扰抑制算法[4-9]对C&I干扰难以有效适用[10-12]。为对抗C&I干扰,文献[13-14]提取回波特征参数,利用分类器识别回波类型,由于缺乏必要抑制环节,算法不适用于自卫式干扰。为提高算法适用范围,文献[15]从C&I干扰假目标生成机理出发,设计了一种多普勒稀疏敏感波形,用于抑制干扰在多普勒上的连续输出,但波形设计会增加发射机复杂度,且所设计波形多普勒容许度较低。文献[16]以LFM雷达中一个相干处理间隔(coherent process interval, CPI)回波为处理对象,通过快慢时间域联合处理,估计干扰位置、幅度等参数重构干扰信号,通过对消实现干扰抑制,但全参数估计较为复杂,累积误差对干扰对消效果影响较大。考虑到C&I干扰波形与间歇采样转发干扰相似[17],频谱由雷达信号频谱叠加而成,干扰信号等同于多分量移频干扰。对于单分量移频干扰,其匹配输出峰值位置取决于发射信号调频斜率和移频量[18-19],当发射信号脉间调频斜率捷变[20-21],由于不同重复周期内假目标快时间位置不同,经相参积累可达成干扰抑制目的,理论上该方法同样可抑制C&I干扰,但脉间调频斜率捷变同样会增加发射机复杂度。
针对上述问题,以不具备调频斜率捷变常规LFM雷达抗自卫式C&I干扰为背景,提出基于回波预处理和相参积累的干扰抑制算法。首先,对回波慢时间做快速傅里叶变换(fast Fourier transform, FFT)估计回波时延(快时间不做处理);其次,根据回波时延设置距离窗截取受干扰回波段;再次,设计M种不同调频斜率LFM参考信号(M为相参积累个数),分别对雷达发射信号和各重复周期回波进行乘积调制;然后,以调制后的发射信号为匹配信号,依次对调制后各重复周期回波进行脉冲压缩,改变不同重复周期假目标快时间位置分布;最后,对预处理回波慢时间相参积累,实现干扰抑制。
1 干扰特性分析
雷达发射LFM脉冲信号,零中频复数形式为
s(t)=rect(t/Tp)eiπkt2
(1)
式中:Tp为脉宽,k=B/Tp为调频斜率,B为带宽。根据相位驻留原理,当TpB1时,s(t)频谱可近似表示为
(2)
设采样脉冲串p(t)脉宽为τ、采样周期为Ts,利用p(t)采样雷达信号,复制次N-1次,拼接得到C&I干扰为
(3)

JCI(f)=[sin(πNτf)/sin(πτf)]·
(4)
式中:fs=1/Ts为间歇采样频率;sin(πfNτ)/sin(πfτ)为频域采样函数。式(4)可简化为
JCI(f)=[sin(πNτf)/sin(πτf)]·
(5)
式中:an=sinc(πτnfs)τ/Ts。可以看出,C&I干扰频谱为雷达发射信号频谱周期延拓、幅度加权、线性叠加和频域采样,干扰信号时域可理解为多分量移频干扰(移频量为nfs),由于LFM固有距离-多普勒的耦合特点,自卫式干扰下干扰信号经雷达匹配滤波器生成虚假目标群,且部分假目标导前真实目标。设自卫式干扰机为点目标,径向速度为vt,初始距离为Rt,速度矢量与雷达夹角为0°,目标雷达散射截面(radar cross section, RCS)不起伏,雷达在干扰机方位接收真实回波基带信号为
(6)

(7)
式中:Aj为干扰幅度;fd(tm)为干扰多普勒频率函数。设fd(tm)=0,不考虑慢时间对回波时延影响,雷达接收受干扰回波可简化为
(8)
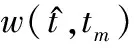
(9)
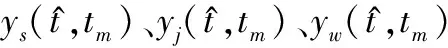
(10)
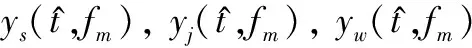
2 干扰抑制原理
2.1 回波预处理
由第1节分析可知,C&I干扰可理解为移频量为nfs的多分量移频干扰。为方便分析,假设C&I干扰包含1个移频分量,即
jCI(t)=s(t)ei2πfst
(11)
令j(t)=jCI(t),根据傅里叶变换频移性质,得到j(t)频谱为
(12)
忽略常复数项e-i4πRt/λ,由式(8)可知,第1个脉冲重复周期雷达接收回波信号为
xr(t)=σs(t-t0)+Ajj(t-t0)+w(t)
(13)

yr(t)=ys(t)+yj(t)+yw(t)=σTp·
sinc[πB(t-t0)]+yw(t)+Aj(Tp-|fs|/k)·
sinc[π(B-|fs|)(t-t0+fs/k)]eiπfs(t-t0)
(14)
式中:ys(t),yj(t),yw(t)分别为第一个重复周期真实回波、干扰分量和噪声脉压结果,真实回波、干扰分量脉压后均为sinc函数,峰值位置分别为t0和t0-fs/k。设距离窗覆盖真实回波与干扰信号[22-23],距离范围为R1~R2,则距离窗可表示为
win(t)=rect[(t-t1)/Tw]
(15)
式中:Tw=2(R2-R1)/c为窗宽度;t1=(R1+R2)/c为窗中心。根据距离窗设计参考信号
ref1(t)=win(t)eiπk1(t-t1)2
(16)
式中:k1为参考信号调频斜率,且k1>-k。利用参考信号对第1个重复周期回波进行乘积调制,得到
(17)
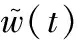
(18)
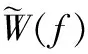
(19)
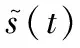
(20)
(21)
(22)

(23)
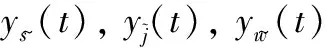
(24)
(25)
当t1=t0时,调制后的真实回波脉压峰值位置为0,与参考信号调频斜率k1无关,而干扰分量峰值位置为-fs/(k+k1),与k1有关。如果对M个重复周期回波使用M种不同调频斜率参考信号调制,真实回波脉压峰值位置恒等于0,而干扰峰值位置均不相同,对预处理回波慢时间相参积累可实现干扰抑制。
2.2 回波时延估计
回波预处理要求距离窗中心t1=t0,为估计回波时延,忽略常复数项e-i4πRt/λ,重写式(8)为
(26)
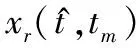
(27)

(28)
对式(28)进行一阶差分即可估计回波时延。综上所述,图1给出了干扰抑制流程。图1中设计参考信号,调频斜率的选取应确保参考信号及调制后回波、雷达信号满足采样定理[24-25]。
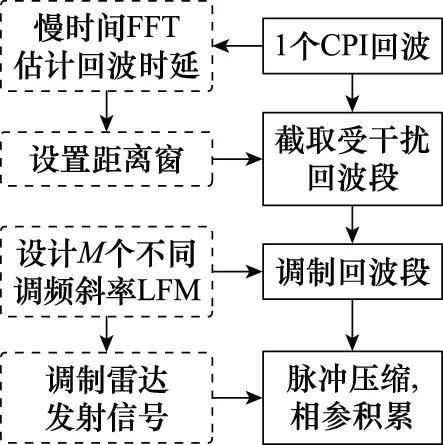
图1 干扰抑制流程Fig.1 Jamming suppression process
3 仿真结果与分析
3.1 参数设置
设雷达载频为0.4 GHz,重频为2 KHz,发射信号为LFM脉冲信号,脉冲宽度为0.1 ms,带宽为4 MHz,采样频率为带宽的4倍,相参积累个数设置为128;干扰机(真实目标)多普勒频率为250 Hz,径向距离为30 km,回波幅度为1 V,根据回波幅度确定信噪比(signal to noise ratio, SNR)和干信比(jamming to signal ratio, JSR);C&I干扰利用脉冲串(采样周期为20 μs,采样脉宽为5 μs)采样雷达信号复制3次生成。
3.2 算法流程仿真分析
设SNR为-10 dB、JSR为20 dB,图2为1个CPI受干扰回波。对回波快时间脉冲压缩、慢时间相参积累,结果如图3所示。C&I干扰经相参积累生成分布真实目标前后相干假目标串,假目标宽度约20 km。

图2 1个CPI回波Fig.2 Echo signal within a CPI

图3 受干扰回波相参积累结果Fig.3 Result of jammed echo coherent integration
根据图1干扰抑制流程,对原始回波慢时间作FFT,结果如图4所示。可以看出,即使不对回波进行快时间脉冲压缩,真实回波和干扰信号同样能够获得相参处理处理增益,与理论分析一致。对慢时间FFT结果取包络,沿快时间求和,结果如图5所示,真实目标径向速度为97.44 m/s。取对应快时间信号,一阶差分结果如图6所示,估计得到真实目标径向距离为30 km,与仿真参数一致。根据虚假目标分布范围,设置宽度45 km距离窗(中心位置为37.5 km),截取受干扰回波段。设计128个不同调频斜率LFM参考信号(参考信号调频斜率在-20~60 GHz/s范围内随机选取),以调制后的发射信号为匹配信号,对调制后的各脉冲重复周期回波进行脉冲压缩,预处理结果如图7所示。可以看出,不同重复周期真实目标脉压峰值快时间位置不变,假目标位置均发生变化。对回波预处理结果慢时间相参积累结果如图8所示,虚假目标得到有效抑制。
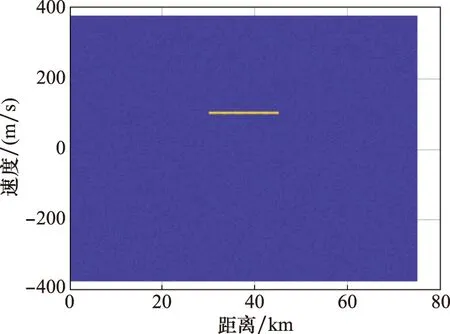
图4 回波慢时间FFT结果Fig.4 Slow-time FFT result of echo
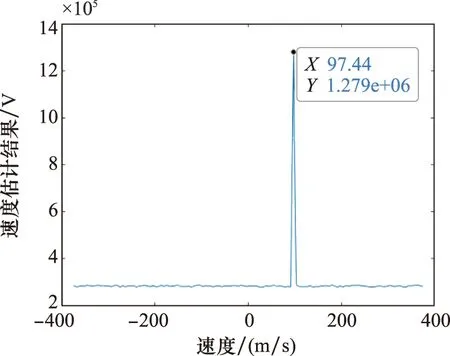
图5 真实目标径向速度估计结果Fig.5 Radial velocity estimation result of real target
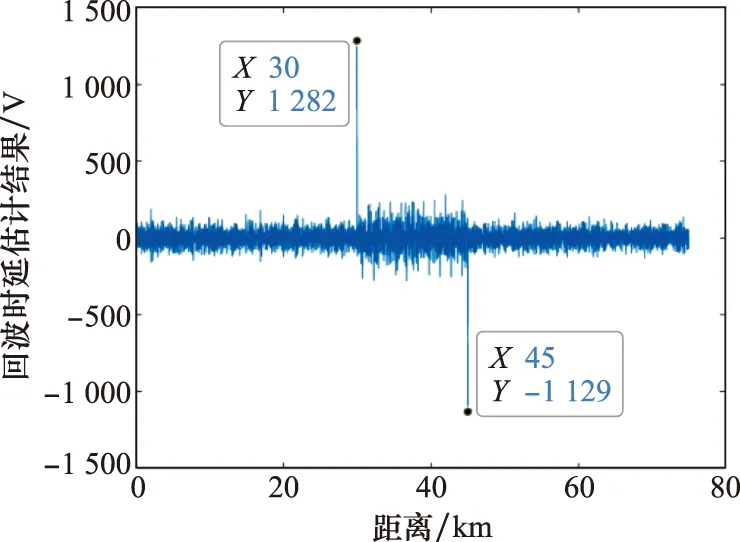
图6 回波时延估计结果Fig.6 Echo delay estimation result

图7 回波预处理结果Fig.7 Echo preprocessing result

图8 干扰抑制效果Fig.8 Jamming suppression effect
3.3 算法效能仿真分析
首先,以平均绝对误差(mean absolute error, MAE)为指标,分析所提慢时间FFT方法回波时延估计精度。为保证通用性,SNR分别取-10 dB、-5 dB和0 dB,JSR取0 dB至50 dB,间隔5 dB,蒙特卡罗500次,回波前沿估计MAE随JSR变化曲线如图9所示。当JSR大于等于15 dB时,不同SNR条件下慢时间方差法[16]和所提方法均能准确估计回波前沿,当JSR小于15 dB时,所提方法估计精度优于慢时间方差法。其次,评估算法虚假目标抑制效能,定义虚假目标抑制率(false target suppression ratio, FTSR)为

图9 回波前沿估计MAE随JSR变化曲线Fig.9 Curves of echo frontier estimation MAE with JSR
(29)
式中:FTSR单位为百分比;num1i为第i次蒙特卡罗抑制前虚假目标数量;num2i为抑制后虚假目标数量。SNR取值同上,JSR取15 dB至50 dB,间隔5 dB,利用二维单元平均恒虚警检测器对抑制前后处理结果进行检测,图10给出了FTSR随JSR变化曲线。两种算法对虚假目标均能达成一定抑制效能,干扰抑制后假目标数量明显减少,FTSR均大于40%。

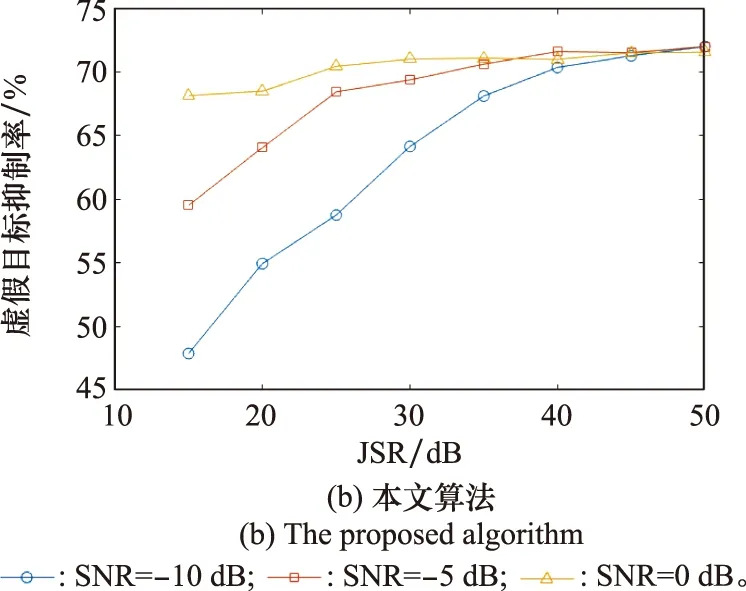
图10 FTSR随JSR变化曲线Fig.10 Changing curves of FTSR with JSR
最后,以真实目标检测率[6](real target detected ratio, RTDR)为指标,评估算法对真实目标检测改善程度。SNR、JSR、蒙特卡罗次数同上,RTDR随JSR变化曲线如图11所示。可以看出,干扰抑制前当JSR大于20 dB时,不同SNR条件下RTDR均为0,雷达检测不到真实目标,文献[16]干扰抑制后,真实目标检测率明显提高,但随JSR的增大RTDR呈一定下降趋势,当JSR增大至45 dB,不同SNR条件下RTDR接近于0,而本文算法不同SNR、JSR条件下RTDR均接近100%,真实目标检测效能优于对比算法。


图11 RTDR随JSR变化曲线Fig.11 Changing curves of RTDR with JSR
4 结 论
自卫式干扰下C&I干扰信号之所以能够获得相参处理增益是因为干扰快时间匹配输出与慢时间无关,对回波进行预处理,使干扰快时间匹配输出与慢时间耦合,慢时间相参积累可实现干扰抑制。基于该思路,提出基于回波预处理和相参积累的C&I干扰抑制算法,算法无需改变雷达发射波形,仅涉及信号层处理,适用常规LFM雷达。仿真结果表明,当SNR大于-10 dB、JSR小于50 dB,所提算法能够有效抑制C&I干扰,干扰抑制后真实目标检测率接近100%,虚假目标抑制率大于45%。
