突出重点目标跟踪的分布式MIMO雷达阵元选取

蒋春启, 郑娜娥, 左 宗, 王 盛, 陈 翔

(1. 战略支援部队信息工程大学数据与目标工程学院, 河南 郑州 450001;2. 电子信息系统复杂电磁环境效应国家重点实验室, 河南 洛阳 471003)

0 引 言

多输入多输出(multiple input multiple output,MIMO)雷达的概念最早提出于2003年[1],主要分为分布式MIMO雷达[2]和集中式MIMO雷达[1]两种。其所具有的分集增益,能够有效抑制干扰、提高分辨率、克服目标的雷达散射截面(radar cross section, RCS)闪烁问题,因此得到了诸多学者和科研机构的广泛关注,研究方向主要集中在波形设计[3-4],检测性能分析及检测器研究[5-8],参数估计[9-11],阵元、目标检测或跟踪[12]、功率和带宽等系统资源的分配[13-21]等。

MIMO雷达系统性能优势离不开阵元、功率、波形、频率等系统资源的合理配置。系统资源的合理优化分配可以有效提高MIMO雷达的系统性能。本文针对系统资源更为丰富的分布式MIMO雷达系统的阵元选取问题展开研究。

通过优化配置,可以用更少的系统资源达到同样的系统性能,降低系统计算复杂度,提升系统综合效能,因此具有重要的研究价值。在这方面已有诸多的研究成果,文献[15]采用启发式算法将阵元选取建模为背包问题(knapsack problem, KP),降低了计算复杂度。文献[16]采用了阵元聚类分组的方法,每个目标只由对应的阵元子集跟踪,分别提出了在复杂度上更有优势的贪婪多起点搜索(greedy multi-start local search, GMLS)算法和在跟踪精度上更有优势的公平多起点搜索(fair multi-start local search, FMLS)算法。文献[17]选取最少阵元的同时尽量降低系统的代价损耗。以GMLS算法为基础,文献[18-19]以GMLS算法和FMLS算法为参考并进行改进,提出了同时兼顾系统性能和计算复杂度的改进GMLS(modified GMLS, MGMLS)算法。文献[19-20]在研究多目标跟踪的阵元选取算法时将目标分为普通目标、可疑目标和危险目标,分别就低跟踪精度要求场景和高跟踪精度要求场景进行讨论,并分别提出了贪婪与公平多起点搜索(greedy and fair multi-start local search, GFMLS)算法和单天线对多目标(one antenna to all targets, OAAT)算法。GFMLS算法数据处理简单,适合处理低跟踪精度要求下不同优先级目标的阵元选取问题,OAAT算法处理数据量大,但可以实现更高要求的目标跟踪性能。

但是以上研究都是针对单任务,实际情况中雷达系统常需要面临多任务的情况,最常见的任务为目标检测和目标跟踪。雷达在执行多任务时,会带来新的资源分配问题,需要考虑任务间的资源分配,当资源不充分时,如何优先保障优先级高的任务。因此,需要对分布式MIMO雷达多任务资源分配技术展开研究。Zhang等在文献[21]中研究了多任务下分布式MIMO雷达的资源分配问题,从提高系统性能和降低复杂度两个方面着手,综合考虑目标跟踪和目标检测,在系统资源上同时考虑阵元、功率和带宽的分配,在阵元选取上采用了改进的粒子群算法,将MIMO雷达的资源分配问题从单任务推进到多任务。但文献[21]在综合考虑不同任务的性能指标时,没有将具有不同量纲的检测概率和定位误差这两个性能指标进行去量纲化处理,将不同量纲的参数强制相加,得出的目标函数缺乏实际意义;同时在进行检测概率的计算时,未能覆盖整个待检测区域,仅考虑了其边界线,实际应用范围受限;且该文献平等对待需跟踪的每个目标,不能适应需要重点跟踪特定目标的情况。当在监视区域内的多个目标中需要重点关注特定目标且系统资源有限时,需要合理进行资源调度以保证重点目标的跟踪性能,确保资源的高效利用。本文针对上述问题,在文献[17， 19-21]的基础上提出了基于改进FMLS(modified FMLS, MFMLS)的阵元选取模型及求解算法。在计算检测概率时,全面考虑整个待检测区域,同时针对多任务的情景,对于不同任务不同性能指标的不同量纲的问题,进行去量纲化和归一化处理,使其具有可比性,在多目标跟踪中突出重点目标的性能保障,使选用的阵元数量尽量少,以此建立优化模型并求解。

1 系统模型

假设目标匀速运动,目标的运动方程为

(1)

(2)

(3)

式中：κ0为噪声的强度；I2为2×2的单位阵；⊗为Kronecker积。

可得目标的运动方程为

(4)

s(t)=[s1(t),s2(t),…,sM(t)]T

(5)

(6)

假设系统能够实现同步,第n个接收阵元接收对第p个目标的低通等效信号[22]为

(7)

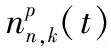
记为

(8)

(9)

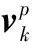
2 重要参数

2.1 目标定位误差的贝叶斯克拉美罗界

(10)

(11)

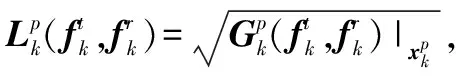
(12)

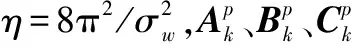
(13)

(14)

(15)

(16)

2.2 目标的检测概率

在考虑分布式MIMO雷达对监视区内特定点的检测时,可以不考虑多普勒效应。以文献[21,25]为参考,在推导检测概率时可采用Neyman-Pearson准则。为便于研究,将噪声考虑为高斯白噪声,雷达发射单脉冲探测信号,利用最大似然比检测器,对于MIMO雷达不同路径,首先进行匹配滤波处理,其次作平方律检波,最后相加[25]。由第m部发射阵元发射由第n部接收阵元接收,故系统应同时有M×N个输出。

将匹配滤波器输出记为Xr,其为一个MN×1向量,当目标不存在时,用g(r(t)|H0)表示信号的概率密度函数,以g(r(t)|H1) 表示目标存在时信号的概率密度函数。则似然比检测为

(17)

若检测门限为δthreshold,当‖Xr‖2≥δthreshold时,表示检测到目标,当‖Xr‖2<δthreshold时表示没有检测到目标。

(18)

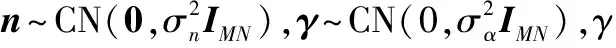
(19)

似然比检测门限δthreshold由虚警概率确定。则相应的虚警概率为

(20)

可以得到检测门限δthreshold为

(21)

由此可以推导出目标检测概率为

(22)

3 阵元选取模型的建立与求解

文献[17]提出的FMLS算法通过遍历所有的初始阵元对,进行多轮启发式选取,能够获得较高的跟踪精度,但没有考虑不同目标不同跟踪精度要求的问题。文献[19-20]提出的OAAT算法将目标分为普通目标、可疑目标和危险目标,就高跟踪精度要求场景进行了讨论,但仍局限于单任务的情形。本文借鉴FMLS算法和OAAT算法,提出了基于MFMLS的阵元选取模型及求解算法。

3.1 模型的建立

在资源有限的情况下进行优化模型的建立。本文为最大限度地节约系统资源,减少阵元使用数量,以发射和接收阵元数量之和为目标函数,并使其最小化。在系统的监视区域内,区分对待不同目标,限定发射阵元、接收阵元的数量总量和最小检测概率,同时限制每次可以使用的阵元使用率,以上述条件为约束条件,建立优化模型如下:

(23)

式中:以最小的阵元集为目标函数,ηp是目标p允许的最大位置估计误差,Pthreshold为检测概率最小阈值,发射阵元的数量不大于M,接收阵元的数量不大于N,系统总的阵元使用率不大于系统容许的最大阵元使用率σ。

3.2 参数预处理

3.2.1 目标位置估计精度误差归一化

由于系统同时承担目标跟踪和目标检测双任务,需要同时考虑检测概率Pd和跟踪目标的位置估计精度误差Emse两项指标。从理论上讲,Pd和Emse的取值范围分别为[0,1] 和[0,+∞),两者具有不同的量纲,难以将系统的跟踪性能和检测性能在同一框架下进行比较和讨论,这也对多任务下的资源分配提出了挑战。一个思路是对不同任务的性能指标参数进行去量纲化和归一化处理,以便使Emse和Pd具有可比性。为此需要将Emse进行归一化处理,使其取值范围由[0,+∞)转为[0,1]。为了实现Emse取值范围的转换,引入参数Emax。Emax为系统进行目标跟踪时可能达到的最大位置估计精度误差,或者说当系统对某一目标的位置估计误差超过Emax时将认定为无效跟踪,失去对目标进行跟踪的意义。Emax的值可通过以下方法进行确定,一是进行仿真分析,以最少的资源进行目标的跟踪,得出系统可能达到的目标定位误差的最大值,以此作为参考,使Emax不小于该值;二是依据实际需求而定,当目标定位误差超过一定值时,跟踪将失去意义,以此作为Emax的值;三是结合雷达系统对目标跟踪的经验积累和仿真分析,人为给出Emax的值。下面给出Emse归一化的具体步骤。

步骤 1给定Emax,使得Emse∈[0,Emax];

步骤 2去量纲处理,令E1=Emse/Emax,使得E1∈[0,1];

经过步骤1和步骤2,虽然已经实现了Emse的归一化处理,使其取值范围与Pd一致。但两者仍然存在区别,Pd的值越大代表检测性能越好,而Emse的值越小表示跟踪性能越好。为了进一步消除不一致,在前两个步骤的基础上继续采取如下步骤。

步骤 3令E2=E1·(-1)+1,使得E2∈[0,1]。

至此完成了Emse的归一化处理。

3.2.2 不同目标的权重处理

对于系统需要跟踪的多个目标,重点目标和普通目标的跟踪精度要求不同,因此在考虑综合跟踪性能时需要对不同的目标区别对待,为此需要引入权重系数。

目标的重要程度与其跟踪精度要求有关,跟踪精度要求越高,目标的重要程度越高,而跟踪精度的数值却越小,因此表示为目标p重要程度的权重系数ξp与跟踪精度数值ηp成反比,即

(24)

式中:ξ为比例系数,在实际应用中ηp为已知条件。假定跟踪目标的数量为Np,所有目标的权重系数之和为1,则有

(25)

通过式(24)和式(25)可求得ξ和ξp。若通过上式确定的ξp还不足以突出重点目标,可以引入人为干扰因子进行调控。例如,当系统需要跟踪的目标为2个,一个为重点目标,一个为普通目标,通过式(24)和式(25)最终求得重点目标的权重系数为ξim,普通目标的权重系数为ξnor,引入人为干扰因子Vξ以进一步加强对重点目标的跟踪,得到最终点目标的权重系数为ξim+Vξ,最终普通目标的权重系数为ξnor-Vξ。

3.2.3 系统综合性能评价

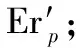
Perk=δ1(Pd-Pthreshold)+

(26)

式中:δ1和δ2分别为系统检测性能和跟踪性能的权重系数。当δ1>δ2时,系统更加侧重于检测任务;当δ1<δ2时,则更加侧重于跟踪任务;当δ1=δ2时,同样对待跟踪任务和检测任务。在实际应用中δ1和δ2的值由操作人员根据实际任务需求人为确定。

当Perk=0时表示系统性能正好达到性能要求;当Perk>0时表示系统性能优于性能要求,且Perk越大性能越好;当Perk<0时表示系统性能劣于性能要求,且Perk越小性能越差。

通过参数预处理,优化模型可重新表示为

(27)

3.3 模型求解

使用穷举法进行阵元选取可以得到系统的最优解,但其计算量达到2(M+N)σ,当阵元数量较多时,计算量非常大。此处假定系统跟踪的目标分为重点目标和普通目标两种,利用MFMLS算法进行阵元选取,具体步骤如下。

步骤 2依据阵元集Amin计算各目标的跟踪性能和检测性能,得到每个目标的跟踪精度误差和检测概率。若系统性能达到要求,进入步骤13,若系统性能不能达到要求,转步骤3。

步骤 3若重点目标的跟踪精度得到满足,转步骤8,否则转步骤4。

步骤 4依据阵元集Amin,并由式计算系统综合性能,记为Per。

步骤 5在阵元集B中选取1个阵元X加入到阵元集Amin中,并更新Amin和B,即Amin=Amin∪{X},B=B{X}。根据更新后的Amin计算系统的综合性能,记为Per′,并计算Δper=Per′-Per。随后在Amin去掉阵元X,再次更新Amin和B,Amin=Amin{X},B=B∪{X}。

步骤 6重复步骤5,遍历集合B中的每一个阵元,得到使Δper取得最大值的阵元X′,将阵元X′加入到集Amin中,并更新Amin和B,即Amin=Amin∪{X′},B=B{X′}。

步骤 7重复步骤4～步骤6,直到重点目标的跟踪性能得到满足或者Amin中阵元是数量达到系统容许的最大阵元使用率。若Amin中阵元数量达到系统容许的最大阵元使用率,转步骤13,否则转步骤8。

步骤 8依据阵元集Amin计算对不同特定目标的跟踪性能和检测性能,得到每个目标的跟踪精度误差和检测概率。若系统性能达到要求,转步骤13,若系统性能不能达到要求,转步骤9。

步骤 9依据阵元集Amin,忽略掉重点目标并由式(26)计算系统综合性能,记为Per。

步骤 10在阵元集B中选取1个阵元X加入到阵元集Amin中,并更新Amin和B,即Amin=Amin∪{X},B=B{X}。根据更新后的Amin忽略掉重点目标并计算系统的综合性能,记为Per′,并计算Δper=Per′-Per。随后在Amin去掉阵元X,再次更新Amin和B,Amin=Amin{X},B=B∪{X}。

步骤 11重复步骤9,遍历集合B中的每一个阵元,得到使Δper取得最大值的阵元X′,将阵元X′加入到集Amin中,并更新Amin和B,即Amin=Amin∪{X′},B=B{X′}。

步骤 12重复步骤8至步骤10,直到系统性能得到满足或者Amin中阵元是数量达到系统容许的最大阵元使用率。

步骤 13重复步骤1～步骤12,遍历所有的初始阵元对,得到诸多阵元集Amin。在诸多的阵元集Amin中选择在满足系统性能且阵元数量最少的阵元集合,若有多个阵元数量同样少的阵元集合,则选择其中综合性能最好的阵元集合;若系统性能不能得到满足,则在诸多的阵元集Amin中选择能够满足重点目标跟踪性能并尽量提高其余性能的阵元集;若重点目标的跟踪性能不能得到满足,则选择系统综合性能最好的阵元集。

3.4 算法复杂度分析

进行阵元选取时,不同算法的复杂度不同,穷举法需要进行2(M+N)σ次阵元选取。MFMLS算法最多需要进行((M+N)σ-2)((M+N)σ-1)MN/2次阵元选取,通过对比可以看出,当系统的阵元数量较多时,本文算法复杂度降低明显。

4 仿真实验与分析

假设分布式MIMO雷达系统分布在6 km×6 km的二维笛卡尔坐标系内,发射阵元数M=8,接收阵元数N=8,形成圆形雷达阵,雷达使用使用率σ=0.75。假定待跟踪的目标数量为NQ=3,目标初始位置为(-2 800,1 000) m、(-150,800) m和(-150,600) m,以60 m/s的速度沿不同方向运动。第一个目标为重点目标,位置估计精度要求为η=9 m,加入人为干扰因子后其权重系数ξ1=0.9;另两个目标为普通目标,位置估计精度要求为η=18 m,加入人为干扰因子后其权重系数ξ2=ξ3=0.05。检测概率最小阈值要求为Pd≥0.9,计算检测概率时,平等对待监视区域内的每一个点。以Δt=2 s的时间间隔进行取样观测,从观测数据中取12帧数据进行对比分析。每个发射阵元用于不同任务的发射功率均为pmax=1 500 W,信号有效带宽、有效时宽、波长分别为1.5 MHz、10 μs、0.3 m,脉冲重复频率为fr=53 kHz。假设系统中目标对雷达各方向散射截面积均相同,取散射系数均为0.9。此处平等对待不同任务,故取δ1=δ2=1,同时取Emax=50 m。仿真采用Num=500次蒙特卡罗进行统计平均。

首先给出阵元在系统中的空间位置及目标的运动轨迹,如图1所示。

图1 雷达与目标的位置及目标的运动轨迹Fig.1 Radar and target position and target’s motion trajectory

为了验证本文算法的有效性,此处将MFMLS算法与其他算法进行比较。一是最少阵元数量穷举法,用穷举法寻找满足系统性能且阵元数量最少的阵元集,将此处的穷举法称为最少阵元数量穷举法。二是首先利用MFMLS算法得到阵元数量,其次用该阵元数量为参数,利用穷举法进行阵元选取,此时,将其称为固定阵元数量穷举法;三是首先利用MFMLS算法得到阵元数量,其次用该阵元数量为参数,随机选取发射和接收阵元,将这种方法称为随机算法。图2～图5分别给出了4种算法在检测概率和3个跟踪目标定位误差方面的对比。可以看到,随机算法无法满足系统的检测性能要求,也不能满足重点目标的跟踪精度要求,不区分地对待3个跟踪目标;而MFMLS算法在各方面性能上均和固定阵元数量穷举法接近,且部分优于最少阵元数量穷举法,三者均能满足系统性能要求,突出对重点目标的跟踪。

图2 检测概率对比Fig.2 Comparison of detection probability

图3 目标1位置估计误差对比Fig.3 Comparison of position estimation error of target 1

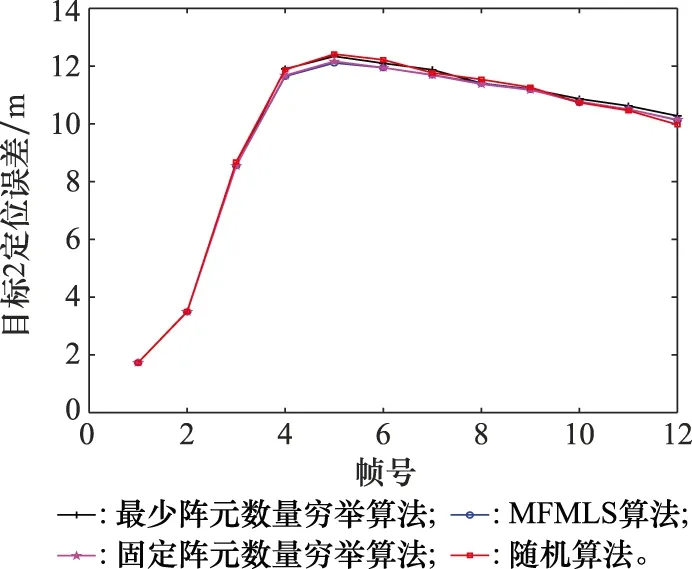
图4 目标2位置估计误差对比Fig.4 Comparison of position estimation error of target 2

图5 目标3位置估计误差对比Fig.5 Comparison of position estimation error of target 3

从以上分析上可知,MFMLS算法能够满足系统各个单方面的性能要求,下面进行系统综合性能分析。图6给出了4种算法的综合性能对比图,可以看到MFMLS算法的综合性能优于随机法,与固定阵元数量穷举法接近,且由于在阵元数量上不能达到最少,故在性能上相对于最少数量穷举法也表现出了一定的优越性。除了随机法没能达到系统的性能要求外,其余方法均达到了要求,这时MFMLS算法便在计算复杂度上便体现了优势。图7是计算复杂度对比,可以看出,相对于最少阵元数量穷举法和固定阵元数量穷举法,MFMLS算法在系统计算量上均能得到大幅降低。进一步由图7中数据分析可知,MFMLS算法在不同帧相对于最少数量穷举法的计算复杂度的降幅均在93%以上,相对于固定阵元数量穷举法降幅在35%～65%。在阵元数量上,最少阵元数量穷举法能够在满足性能的前提下达到最少阵元,由于涉及到多任务而且不同目标的跟踪精度要求也不同,难以完全做到阵元数量最少,但500次蒙特卡罗平均值后,MFMLS算法在阵元数量上接近最少阵元数量穷举法。图8给出了阵元数量对比图。

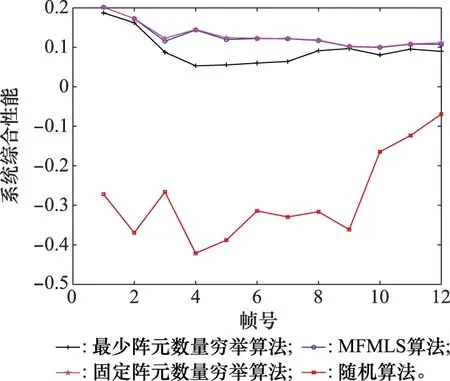
图6 综合性能对比图Fig.6 Comparison of comprehensive performance

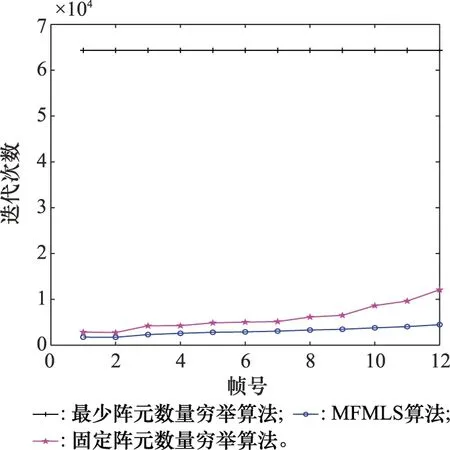
图7 计算复杂度对比Fig.7 Comparison of computational complexity

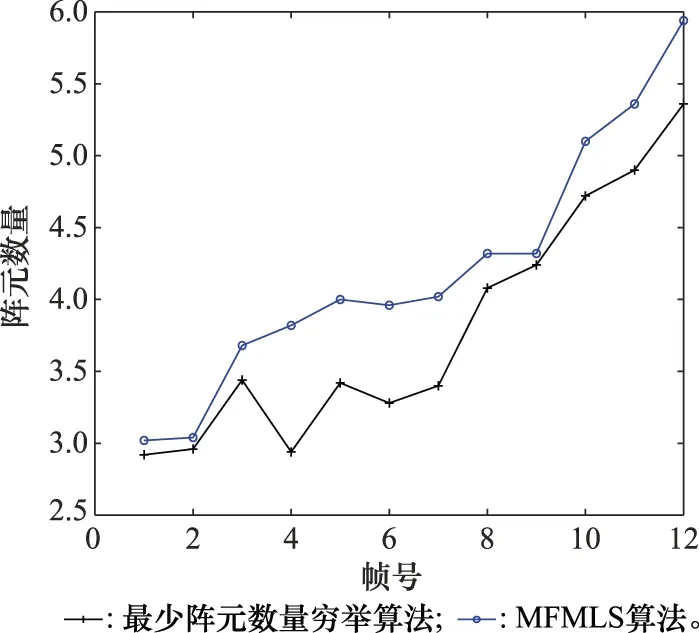
图8 阵元数量对比Fig.8 Comparison of the number of antennas

5 结 论

本文研究了多目标跟踪和目标检测多任务下的分布式MIMO雷达的阵元选取问题,且不同目标具有不同的跟踪精度误差。为了突出对重点目标的跟踪并兼顾系统的整体性能,本文提出了基于MFMLS的阵元选取模型及求解算法。通过仿真实验,利用MFMLS算法进行阵元选取能够满足系统性能要求,在系统性能上本文算法优于随机算法,在计算复杂度上,本文算法相对于最少阵元数量穷举算法和固定阵元数量穷举算法均有大幅下降,由此验证了本文算法的有效性。但本文的研究同样存在局限性,需要展开进一步的研究,如在目标运动规律上,本文的跟踪目标为匀速运动,多任务下机动目标的跟踪仍需研究;在目标数量上,本文考虑的跟踪目标数量较少,大规模集群目标的跟踪仍需研究;在系统资源上,本文仅考虑了阵元因素,多任务多资源因素下的资源分配仍需研究。