基于均匀圆阵伪协方差矩阵的单快拍测向方法

汪 鹏, 熊 钊, 于俊鹏, 田 勇, 李万春

(电子科技大学信息与通信工程学院, 四川 成都 611731)

0 引 言

波达方向(direction of arrival,DOA)估计是许多科研学者在阵列信号处理中关注和研究的重要领域[1],在军用以及民用领域有着广泛的应用,如雷达探测[2-3]、电子对抗[4]、声纳[5]、无线传感器网络[6-7]等。子空间类超分辨算法如多重信号分类(multiple signal classification,MUSIC)算法[8]和信号参数旋转不变(estimating signal parameter via rotational invariance techniques,ESPRIT)算法[9]通常要求接收数据的协方差矩阵的秩等于信源个数,需要较多的快拍数来求得信号子空间和噪声子空间从而提高估计的精准度[10],是DOA估计常见的两类算法。在军事对抗过程中,信号出现的时间往往较短而且具有较快的跳变速度,使得信号难以被侦察到,以及其他要求系统具有很高的实时性和一些物理限制的场景,这意味着DOA估计使用的快拍数只能很少,甚至在最坏的情况下只有单快拍[11]。单快拍测向是短快拍测向的极限情况,近年来在传统多快拍阵列测向的基础上,国内外学者同样对其进行了广泛的研究,提出了在不同条件下的单快拍测向算法[1,10,12-14]。

在实际应用中,相比均匀线阵(uniform linear array,ULA),均匀圆阵(uniform circular array,UCA) 能够在360°全方位进行测向,可以估计阵列平面内无镜像模糊的方位角和俯仰角,且在不同方位有着均匀的测向精度,因此有着更广泛的应用[15]。传统的单快拍测向算法一般要求阵列流型具有Vandermonde结构,使得许多适用于ULA 的单快拍测向算法无法直接应用在不具有Vandermonde矩阵结构的UCA上[16]。为解决此问题,一般通过模式空间变换法[17]将 UCA 变换为虚拟均匀线阵(virtual ULA, VULA),间接地使其具有Vandermonde阵列结构。基于模式空间变换进行UCA 的测向算法主要分为两大类:① 空间平滑类算法,如经典的模式空间平滑(mode spatial smoothing,MODESS)算法、模式空间前后向平滑(mode forward-backward spatial smoothing,MODE-FBSS)算法等,此类算法计算复杂度高、平滑次数不易确定[18];② 基于特征矢量重构或数据矩阵重构类算法,如模式空间Toeplitz矩阵重构算法(mode Toeplitz,MODETOEP)、基于最大特征矢量的均匀圆阵解相干算法(mode and maximum eigenvector,MME)等[19]。

综上分析,基于UCA的单快拍测向算法很多,针对以上问题,提出了一种新的伪协方差矩阵的构造方法,解决了接收数据只有单快拍所造成的协方差矩阵秩不够的问题,同时结合模式空间变换,将UCA转换为具有Vandermonde形式的VULA,实现了UCA的单快拍测向。

1 基于MODE-FBSS的单快拍测向

1.1 空间平滑法

假设一个标准的ULA,含有M个相同的全向阵元,相邻阵元间距为d。现有N个窄带远场信号分别以角度θi入射,则第p个阵元接收的数据为

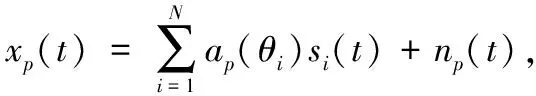
(1)

空间平滑算法利用了ULA的平移不变性,将m个阵元作为一个子阵,从前向后将所有阵元分为彼此重叠的l个子阵。如图1所示,为前向空间平滑算法原理图,可以得到M=l+m-1。

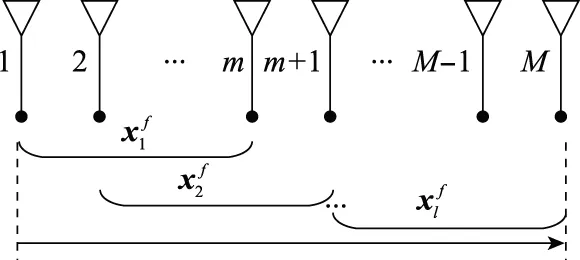
图1 前向空间平滑原理图Fig.1 Schematic diagram of forward spatial smoothing

以第1个子阵为参考子阵,第k个子阵接收的数据可表示为

(2)

式中：

(3)

式中:βi=2πdsinθi/λ。那么,该子阵接收数据的协方差矩阵为

(4)

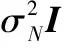
采用前向空间平滑算法求出每个子阵的协方差矩阵,再利用其均值来得到满秩的协方差矩阵,则修正后的协方差矩阵为

(5)

从式(5)可知,如果每个子阵的阵元数目m≥N,那么当p≥N时,经过上述方法得到的是一个满秩的数据协方差矩阵Rf。后向空间平滑算法对矩阵进行划分的过程如图2所示,类似地能够求出协方差矩阵Rb。采用前后向空间平滑算法,将上述求得的协方差矩阵Rf和Rb取平均,计算求出双向空间平滑协方差矩阵Rfb=(Rf+Rb)/2,然后对满秩的协方差矩阵Rfb进行特征分解,再使用MUSIC算法来完成单快拍测向。

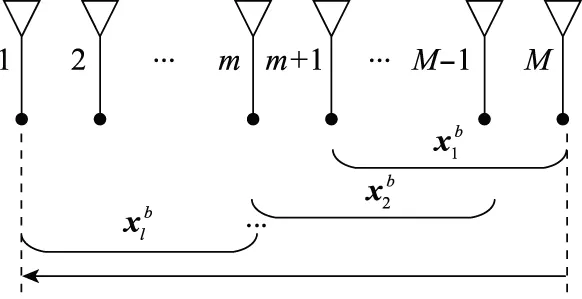
图2 后向空间平滑原理图Fig.2 Schematic diagram of backward spatial smoothing

1.2 模式空间法

UCA的阵列流型不具有Vandermonde形式,为此要进行模式空间法变换转化为VULA。假设在xoy平面上的UCA,其半径为R,圆周上均匀分布了M个各向同性的阵元,N个窄带远场信号源入射到UCA上,每个信号只接收到单快拍。图3为UCA的结构示意图,取圆心O为参考点,可以用(θi,φi)来描述DOA估计,方位角θ为入射信号在xoy平面上的投影与x轴在逆时针方向上的夹角,范围为[0°,360°);俯仰角φ为入射信号与z轴的夹角范围为[0°,90°]。同时,假设所有信号源都与UCA共面,即俯仰角φ=90°[20]。

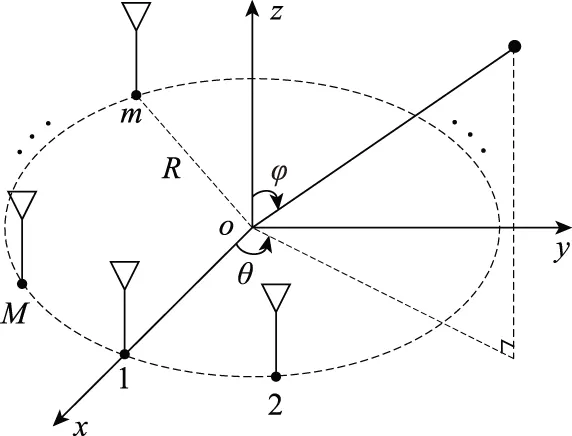
图3 UCA模型Fig.3 UCA model

由于在模式空间变换后噪声功率发生改变,避免噪声功率分布不均的问题,假设当无噪声时,阵元p上的快拍数据为

(6)

式中：波数β=2πR/λ。对应的导向矢量为

(7)

对阵列上所有阵元接收的快拍数据作空间离散傅里叶变换有:

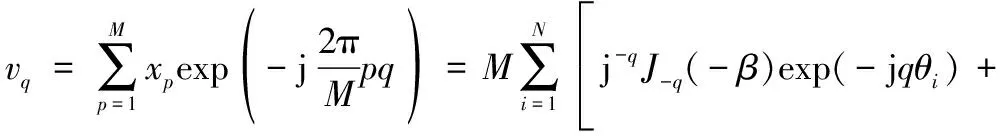
(8)

-K≤q≤K

(9)

(10)

即:

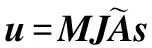
(11)

那么,式(8)的矩阵形式表示为

(12)

可以得到:

u=FHx

(13)

FHF=MI

(14)

F是一个正交矩阵。由式(11)和式(13)可得预处理矩阵T:

(15)

对UCA接收数据进行模式空间变换后得到了一个阵元数为M′=2K+1的VULA,其阵列接收数据为

(16)

为了补充协方差矩阵的秩可采用前文所述的空间平滑法,然后再通过MUSIC等算法进行测向。

2 基于改进的伪协方差矩阵的单快拍测向

2.1 改进的伪协方差矩阵构造原理

由式(10)可知,UCA经过模式空间变换后的VULA阵列流型为

(17)

其导向矢量为

(18)

式中：k=1,2,…,M′；i=1,2,…,N。

VULA与ULA的阵列结构均具有Vandermonde形式,若将传统基于ULA的伪协方差矩阵的构造方法直接用于VULA,得到的协方差矩阵为

(19)

由式(19)可知,此时的R需要x1+M′,x2+M′,…,xK+M′等数据,而VULA只有M′个阵元,对应只有M′个数据,因此通过该方法无法构造伪协方差矩阵。基于此,本文只取VULA的第K+1个阵元到第M′个阵元上的数据[21],则阵元接收的数据为

(20)

令h=k-K,则式(20)可写成:

(21)

此时导向矢量变为

ak(θi)=ej(k-1)θi,i=1,2…,N

(22)

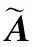
(23)

此时构造的伪协方差矩阵为

(24)

其中,

(25)

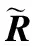
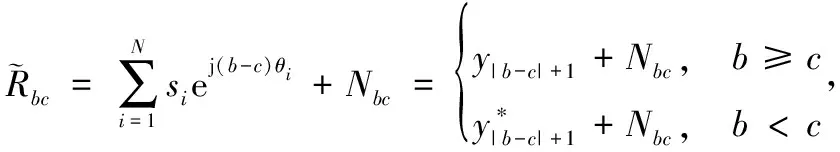
(26)

因此构造的伪协方差矩阵为

(27)

2.2 算法步骤总结

表1 算法实现步骤Table 1 Algorithm implementation steps

3 仿真实验与分析

根据上述的分析,本文分别采用MODE-FBSS算法与改进后的伪协方差矩阵算法在UCA进行DOA估计,通过多次仿真实验分析两种算法的方位估计均方根误差(root mean squard error, RMSE)随信噪比(signal to noise ratio, SNR)、阵元数量(M)的变化关系,方位估计均方根误差定义如下:

(28)

设定UCA的阵元数M为21个,阵元间隔为半波长,圆阵半径R为1.5λ,入射的窄带远场信号数为4,入射的方位角分别为75°、130°、190°、340°,俯仰角均为90°,默认SNR为20 dB,快拍数为1,蒙特卡罗实验次数为1 000。

仿真 1两种算法的空间谱估计结果的比较

仿真得到的最大相位模式数为9,VULA阵元数为19,采用两种算法的仿真结果如图4所示。从图4中可以看出,通过本文算法和MODE-FBSS算法对4个信号源均测出了正确的到达方向,但经本文提出的算法仿真得到的空间谱的旁瓣压制得更低点,谱峰稍尖锐,分辨信号源的能力更高。

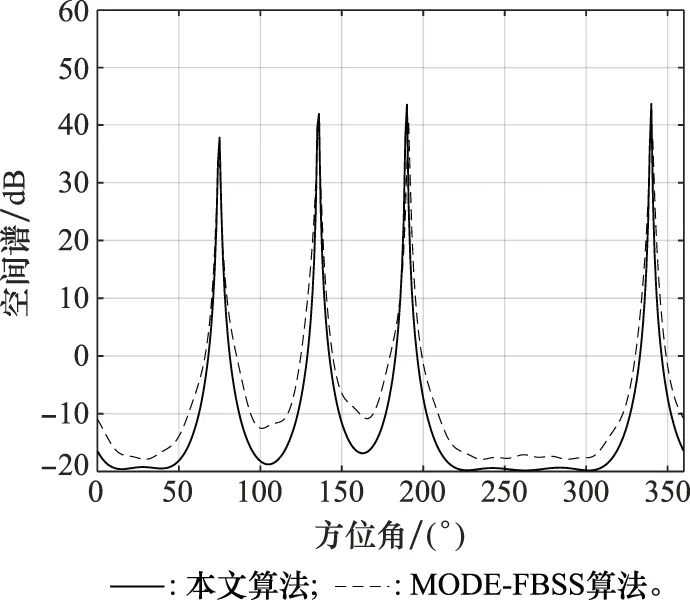
图4 两种算法空间谱估计图Fig.4 Spatial spectrum estimation of two algorithms

仿真 2SNR对两种算法估计性能的比较

本次仿真的SNR从0 dB到40 dB以5 dB的间隔变化,其他条件保持不变。如图5所示,为RMSE随SNR的变化曲线。由仿真结果可知,两种算法的RMSE均随着SNR的增加而降低,且二者的RMSE差值随着SNR的增加而越来越大。在相同SNR的条件下,采用本文提出的算法得到的RMSE要比采用MODE-FBSS算法的低,因此本文提出的算法总体性能要优于MODE-FBSS。

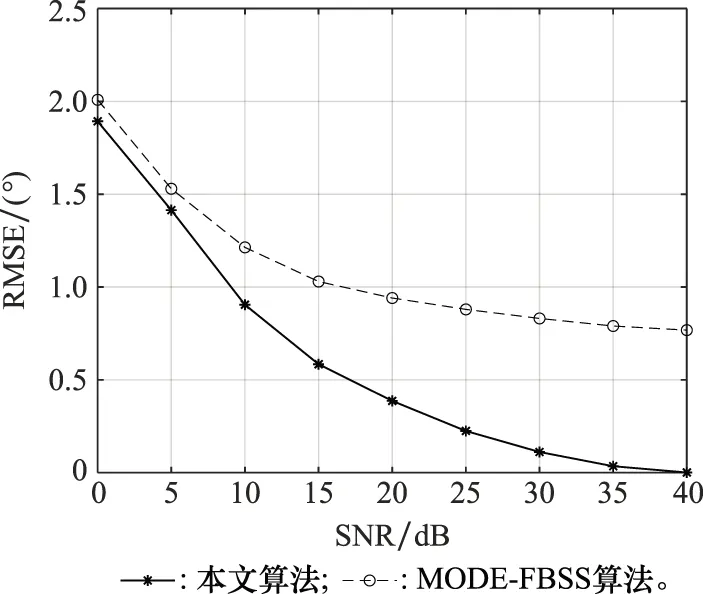
图5 两种算法的估计性能随SNR变化曲线Fig.5 Estimation performance with SNR for the two algorithms

仿真 3基于改进后与原协方差矩阵的两种算法的估计性能比较

本次仿真SNR从0 dB到40 dB以5 dB的间隔变化,仿真得到DOA估计的RMSE随SNR的变化曲线如图6所示。由仿真结果可知,基于ULA构造伪协方差矩阵的方法若直接用于UCA模式空间变换后的虚拟线阵,进行单快拍测向性能较差;而改进后的伪协方差矩阵用于UCA的单快拍测向时,其RMSE随SNR的增加而逐渐减小,并趋向于0,估计性能明显较好。

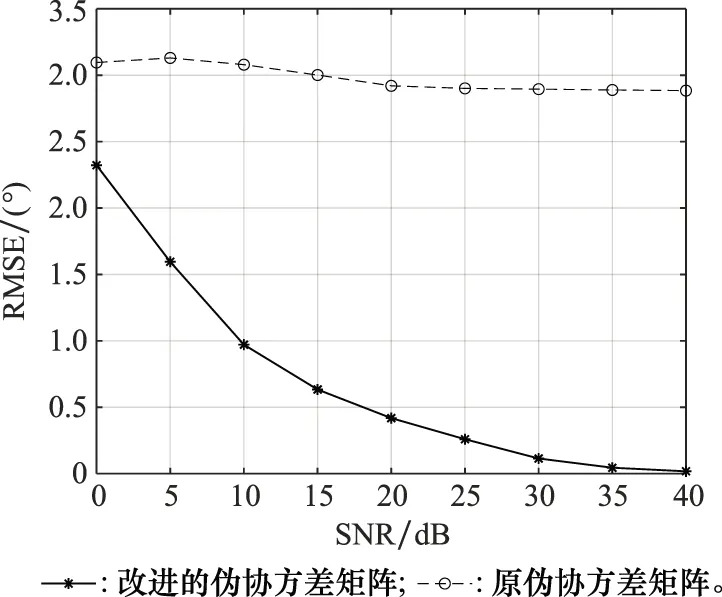
图6 改进的与原伪协方差矩阵法的性能比较Fig.6 Performance comparison between improved and original pseudo-covariance matrix methods

仿真 4M对两种算法估计性能的比较

UCA阵元数量M增加到40,步长为4,图7所示为RMSE随阵元数M的变化曲线。由仿真结果可知,采用本文提出的算法得到的RMSE随着阵元数的增加而减小并趋于平缓,性能明显优于MODE-FBSS算法。

图7 两种算法的估计性能随阵元数变化曲线Fig.7 Estimation performance with number of array elements for the two algorithms

4 结 论

在诸多现实场景下,侦察接收到的消息常常是有限的,为了有效地进行单快拍测向,本文利用改进的伪协方差矩阵提出了一种基于UCA的单快拍测向算法。通过仿真可知,传统的适用于ULA伪协方差矩阵的构造方法不能直接用在与UCA有关问题上,因此对传统的伪协方差的构造方法进行改进,利用模式空间变换得到的具有Vandermonde形式的虚拟线阵,然后再对虚拟线阵的数据完成进一步地处理,实现了UCA的单快拍测向。通过对比仿真,分析验证了本文提出算法的有效性。