基于分散PV-BES协调架构的孤岛直流微网电压控制

马红明，耿泉峰 ，霍雨佳，王朔

（1.国网河北省电力有限公司营销服务中心，河北 石家庄 050000；2.浙江工业大学机械工程学院，浙江 杭州 310023）

近年来，光伏发电（photovoltaic，PV）已成为主流分布式能源。PV具有分布广、零排放的优点，是边远地区很有前景的能源解决方案[1-3]。与传统集中发电相比，PV具有分布式特性，它依靠微电网（microgrid，MG），是利用太阳能的有效途径[4-7]。MG集发电、负荷、储能于一体，可以持续稳定地提供电能，支持多种负荷，同时保持低前期成本和较短前置时间。除了传统MG外，可扩展插拔式（plug-n-play，PnP）MG已经成为学术界和工业界研究的热点[8-10]。PnP MG可以进一步降低设计和安装成本，并允许用户在需求增长时有机地增加电网的支撑能力。直流MG因其可靠性、效率高，控制简单等优点而倍受关注，有利于孤岛PnP MG的应用[11]。目前，PnP MG已经成为解决农村地区能源贫困问题的一个有效解决方案。为了实现PnP MG的高模块化和可扩展性，设计的关键因素与传统MG有较大不同[12]，除了高度模块化的硬件结构外，还需要开发完全独立于通信的分散控制系统，其中，下垂控制是最常用的分散控制方法，可实现MG的电压调节和功率分配。与并网MG系统不同的是，在孤岛MG系统中，没有主电网支撑能量和稳定电压，功率平衡需要由MG自身调节来维持。通常采用下垂控制系统来平衡发电与负载之间的功率不平衡。然而，由于电池储能（battery energy storage，BES）系统的荷电状态（SOC）限制和充放电功率限制，BES系统的调节能力有限。因此，当BES饱和时，需要用PV发电作为母线调压器。PV除了最大功率点跟踪（MPPT）模式外，光伏变流器还应能够在下垂控制模式下运行，以提高系统的直流母线调压能力[13]。为了在无通信的情况下同时实现PnP MG的功率分配和模式转换，文献[14]提出了一种带直流母线信号的分散模式自适应控制技术，以实现无通信的下垂控制协调。文献[15]将分散控制方法应用于PnP微电网系统的远程电气化。这种分散控制方法比增加一个中央控制器和一个通信线路具有更高的可靠性、灵活性和可扩展性。除了模式自适应，光伏发电需要能够在母线电压控制模式下运行，而目前大多数光伏产品只考虑最大功率跟踪控制。此外，BES系统通常采用传统的下垂控制[16-17]。应用于光伏发电时，其性能会变差。在母线控制模式下，特别是在轻载情况下，母线电压调节很弱。由于气候条件的不同，光伏参数变化很大，这也增加了控制系统的设计难度。因此，可能会有非常大的超调量，从而损坏系统或导致安全问题。因此，对于PV来说，在其运行过程中需改进下垂控制，使其既具有鲁棒性，也有一定经济性[18-19]。

为了解决上述问题，本文提出了一种基于PV-BES协调架构的PnP MG电压控制方法，该方法可在PV发电主导模式下，利用BES系统补偿暂态能量，在不增加任何附加元件的情况下，也能保持系统电压在可接受的范围内。此外，该方法属于一种分散式无通信控制，能够无缝模式转换，具有更强的鲁棒性，非常适用于PnP MG。

1 分散PV-BES协调控制设计

图1所示为PnP MG的结构图。

图1 可扩展PnP MG的结构图Fig.1 Scalable Plug-n-Play microgrid

为了在直流微电网中实现PV和BES的PnP特性，本文提出了一种完全非通信的分散控制系统。控制系统分别包含BES变换器和PV变换器的独立控制器。采用所提出的控制方法，当新的光伏组件或BES组件安装到MG中时，现有变流器的控制参数不需要进行任何调整。在存储控制和发电控制两种模式下，均能保持直流环节电压调节的鲁棒性和快速响应。图2为直流母线电压信号的通用下垂协调。

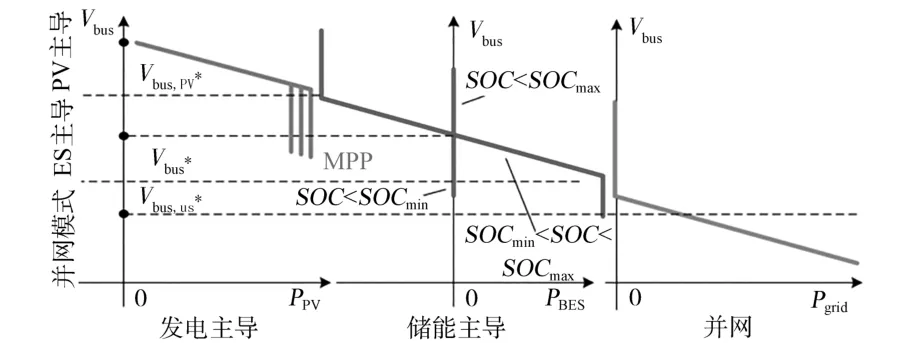
图2 基于直流母线信号的分散模式自适应Fig.2 Decentralized mode adaptive using DC bus signaling

1.1 PV变流器的控制方法

图3为所提模式自适应PV控制图。该控制方法含内环控制PV输出电流、中间环控制PV端电压和外环为V-I下垂控制环。外部环路的输出Vbus经过一个饱和器，其上限设置为MPPT电压VMPP。通过设置PV下垂控制的额定母线电压，使高于BES变换器的额定母线电压，只要BES变换器调节母线电压，PI控制器的输出Vbus将始终饱和到VMPP。当BESs过度充电时，Vbus将比VPV,ref上升得更快，VPV,ref将减小到低于VMPP。因此，降低光伏组件的输出功率，可实现光伏组件的无缝模式转换。值得注意的是VPV,ref的饱和特性要求在下垂控制中增加积分器，这就解释了为什么PV变流器控制采用V-I下垂控制，而不是I-V下垂控制。与典型的V-I下垂控制系统不同，该PV控制器有三个控制回路。它需要两个回路（vPV回路和iPV回路）来稳定PV输出功率，而不是BES应用中简单的电流回路。并且由于MPPT控制的带宽比PV电压环慢得多，在稳态下，iPV=iPV0。因此，可以使用iPV作为最大功率跟踪控制器的参考值，以减少电流传感器的数量，而不是使用iPV0。此外，该方法为V-P下垂控制，利用PV测量的功率代替直流母线侧测量的电流，进一步减少电流传感器的数量。对于提出的PV控制系统，总共只需要一个电流传感器。最大的内部控制环带宽是由开关频率限制的，每个控制环与其相近控制环通常有5～10倍带宽差。因此，增加控制回路的数量会使外回路的动态性能变差。本文提出的BES变流器控制器将提供动态补偿，以帮助在PV主导模式下实现电压调节，以解决上述问题。

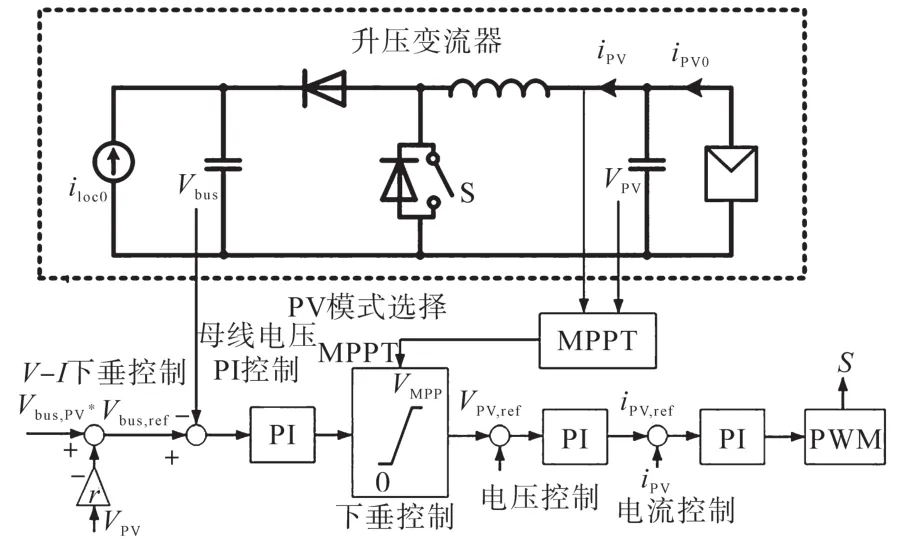
图3 所提模式自适应PV控制图Fig.3 Diagram of PV converter controller with seamless mode selection

1.2 BES变流器的控制方法

如上所述，PV下垂控制在母线电压调节方面的动态性能相对较差。此外，PV变换器的功率流是单向的。因此，在零负载情况下，如果BESs不能进一步吸收能量，由于能量不能消耗，母线电压将保持在峰值过调值。因此，即使在发电控制模式下，也必须保持BES变换器的动态调节能力。与PV变换器不同，BES变换器不需要复杂的模式转换。可使用I-V下垂控制。在I-V下垂控制中，只有一个电流环被使用。带宽可以比V-I下垂控制高很多。随着BES辅助PV下垂控制，在储能主导和发电主导模式下，均能保持高性能的动态响应。

传统I-V下垂控制通过一个低通滤波器（LPF）和一个高通滤波器（HPF）解耦成两条路径。LPF路径能够提供稳定状态下的功率分配和功率均衡能力。采用HPF路径作为动态补偿路径来补偿暂态能量。当LPF和HPF的时间常数相同时，二者的组合性能与传统的I-V下垂控制相似。上述解耦设计具有以下优点：1）不同的电流限制可以放在两个路径上。主功率流由LPF路径决定。HPF路径对能量交换影响不大，对BES的SOC水平影响不大。因此，即使LPF路径饱和，BES动态补偿路径也能保持主动。2）两种路径可采用不同的下垂系数。LPF路径可以有一个较大的值m1来缩小母线电压稳态误差。HPF路径可以有一个相对较小的m2值，以避免噪声的影响。对于稳态分析，可以忽略HPF路径的影响。

本文在BES的I-V下垂控制中增加了SOC项，实现了SOC的自收敛。与现有改进下垂控制不同，该方法在下垂线路上增加了一个离线控制，以更好地适应直流母线电压信号。此外，传统I-V下垂控制的输出电流与电压误差成正比，它包含一个SOC斜坡项。具有附加项时，当BES的SOC水平高于SOC*时，输出电流略有增加；当SOC低于SOC*时，输出电流略有减小。因此，多个BES之间的SOC可以达到收敛。

2 系统稳定性分析

除了下垂控制器外，PV控制器还有一个三重环结构（包括PV电流环、PV电压环和直流母线电压环）。因此，控制参数必须仔细选择，以避免控制回路之间的相互作用。伯德图可以清晰地显示各控制回路的分频，指导各控制回路的设计。对于包括V-I下垂控制器在内的整个系统，由传递函数模型推导出状态空间模型，更便于评价系统的整体性能。

2.1 传递函数模型

图4为带BES HPF补偿的控制方框图。

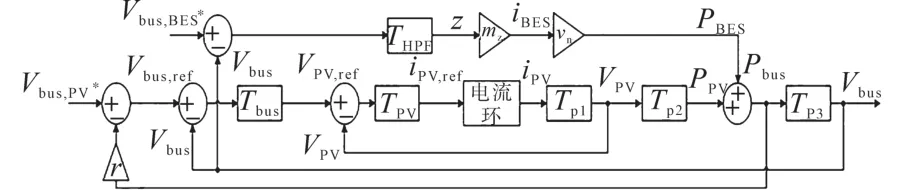
图4 发电主导模式下Vbus下垂控制控制框图Fig.4 Control block diagrams of Vbusdroop control under generation-dominating mode

由图4可得，BES HPF补偿可以给系统增加一个前馈控制路径。光伏变流器的电流控制器可以采用高控制带宽的迟滞控制器或PI控制器来实现。PV电流环的响应速度比外环快得多。为简化研究，PV电流环的闭环传递函数可记为1。PV阵列具有非线性I-V特性。通常线性化的表达式可以写成：

KPV总是负的，通过在光伏电压VPV微分方程中加入扰动：

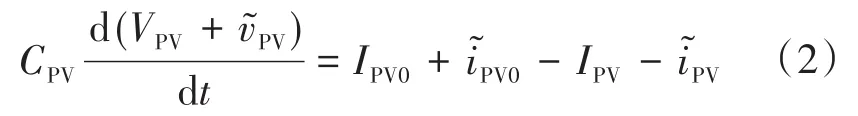
式中：CPV为光伏电容；IPV0为光伏电流初始值。

将式（1）代入式（2），时间Tp1可表示为

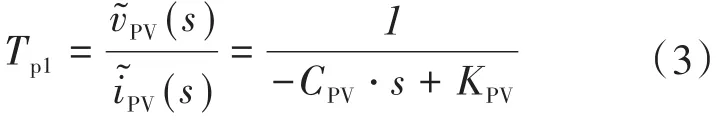
通过在光伏有功功率PPV计算中加入扰动：

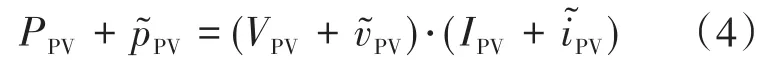
将式（1）代入式（4），时间Tp2可表示为

式中：K′为增益，是一个常数，取决于PV的运行点。

由式（5）可知，MPPT稳态运行时：

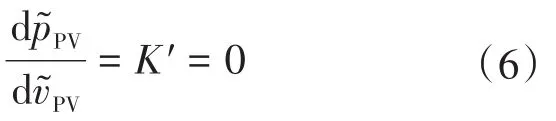
Vbus回路和VPV回路PI控制器的传递函数可表示为

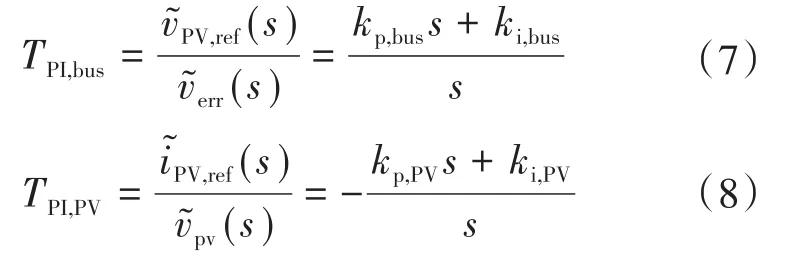
在BES动态补偿回路中HPF传递函数可表示为

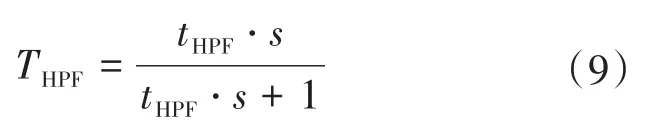
式中：THPF为HPF传递函数；tHPF为HPF时间常数。

2.2 PV电压控制环

由式（8）和式（3），可以得到VPV回路开环传递函数TOL,VPV：

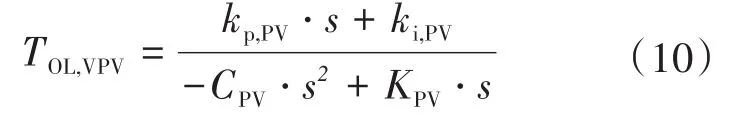
假设PV电流环分频在4 kHz左右（开关频率为20 kHz），VPV回路的分频至少要是其1/5，也就是800 Hz左右。图5为VPV开环传递函数的伯德图。由图5可知，当KPV在-0.01～-0.1范围内变化时，交叉频率保持在717 Hz附近，相位裕度在 88.5°～94.2°范围内，其中，三条曲线分别是KPV为-0.01，-0.1和-0.05时的PV电压开环传递函数曲线，故PV电压环对PV参数变化具有鲁棒性。

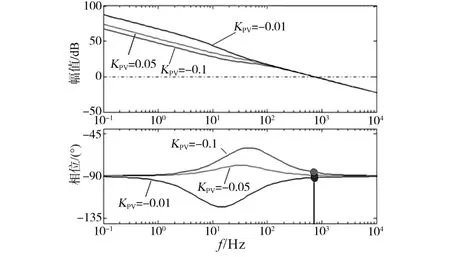
图5 光伏电压回路的伯德图Fig.5 Bode diagrams of PV voltage loop

2.3 直流母线电压控制环

通过使用现有的BESs来实现补偿。虽然在发电主导模式下BES是饱和的，但它仍然可以提供动态补偿，不会造成大量的能量流。控制图见图4，Vbus开环传递函数为

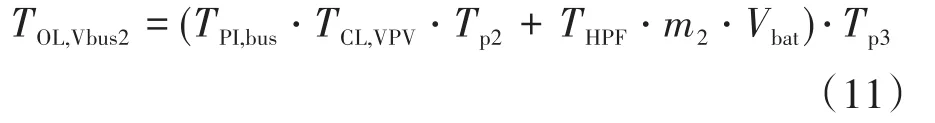
式中：TCL,VPV，Vbat，Tp3分别为PV电压的闭环传递函数、电池电压和时间常数。

图6为BES HDF补偿的母线电压回路伯德图，其中，增益K′是一个常数，取决于PV工作点。图6中，三条曲线分别是K′为1.8，0.02和0.2时的直流母线电压开环传递函数曲线。由图6可知，交叉频率始终保持在1 200 Hz左右，相位裕度K′变化90°左右。尽管PV电压环内部存在限制，但交叉频率仍能保持在较高的值。因此，BES补偿回路作为独立于PV参数的前馈回路，可以使系统对PV参数变化具有更强的电阻性，提高系统的动态性能。因此，采用BES补偿，即使在发电控制模式下，直流母线电压调节也能保持鲁棒性，并具有良好的动态性能。

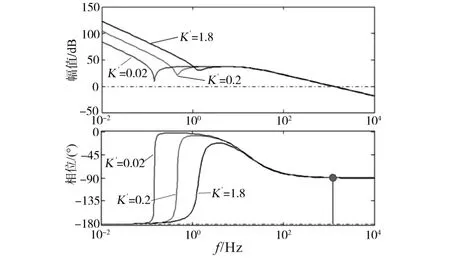
图6 BES HPF补偿的母线电压回路伯德图Fig.6 Bode diagram of bus voltage loop with BES HPF compensation

2.4 基于状态空间模型的系统稳定分析

为了评估包含V-I下垂控制的整个系统的性能，由于下垂控制器与内环输出Pbus之间存在交互作用，传递函数方法将变得过于复杂。因此，利用状态空间模型对系统进行稳定性评估。系统的闭环状态方程可表示为

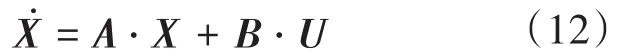
式中：X，A，B，U为状态方程系数。

对于图1所示的系统，可以选择状态向量为

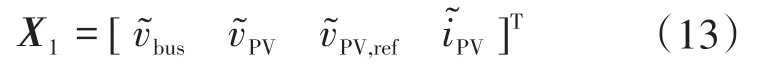
对传递函数进行拉普拉斯逆变换，得到各状态变量的微分方程，最后可得系统矩阵A：

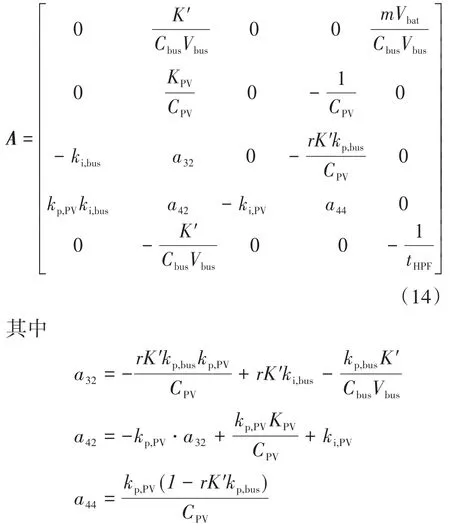
在状态矩阵由式（14）给出的情况下，图7为主导特征值随PV工作点变化情况。

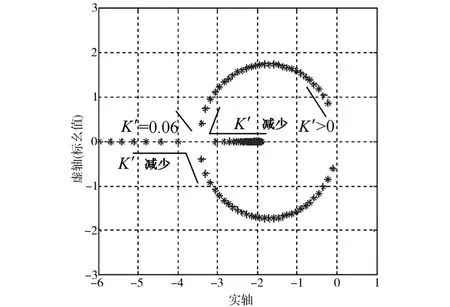
图7 含BES补偿的系统特征值Fig.7 Dominant eigenvalues of overall system

当K′＞0时，系统是稳定的。当K′＜0.06时，主特征值变为一对虚部小的共轭特征值（ω＜1.7 rad/s）。只有当K′＜0.06（几乎在 MPP点上）时，主特征值才会共轭；振荡频率非常低，ω＜1.7 rad/s。但是由于谱仪补偿的引入，谱仪的高频HPF的作用，使得主特征值更接近虚轴，动态响应不可避免地会变慢。

3 仿真分析与实验验证

为验证本文所提方法的可行性与有效性，本文对不同负荷状态下PV变流器控制模式由MPPT控制转变为下垂控制进行仿真和实验研究。仿真系统相关参数如下：储能系统电压，母线电容Cbus=660 μF，控制器参数kp,bus=3.5，ki,bus=100，kp,PV=10，ki,PV=2，内阻r=1/100，光伏电压V*bus,PV=53 V，光伏电容CPV=200μF，控制器参数m1=1，m2=1，时间常数tLPF=0.01，时间常数tHPF=0.01，储能电压VBES=48 V。

图8为无BES HPF补偿的PV-BES下垂控制协调仿真结果。

图8 无BES高功率滤波器补偿时PV-BES协调控制仿真结果Fig.8 Simulation results of PV-BES droop control coordination without BES HPF compensation

由图8可以看出，负载为25 W时，PV暂态时刻母线电压有14%的超调。切换到下垂控制。在负载较轻的情况下，超调量增加到20%，远远超出了可接受的电压波动范围。随着光伏发电额定值的提高或负载的减少，电压峰值甚至可能进一步增加。

采用BES HPF补偿的PV-BES协调控制仿真结果如图9所示。在图9a中，负载为25 W时，PV控制模式切换到下垂控制的暂态母线电压只有4.8%的超调。图9b中2.5 W负载时，超调量仍保持在4.7%左右。虽然母线电压需要较长的时间才能稳定下来，但始终保持在一个非常小的波动范围内，这对MG系统的影响可以忽略不计。采用BES高频滤波器补偿后，BES的功率在暂态时不会立即变化到零，而是缓慢地达到零，从而阻止母线电压的上升。

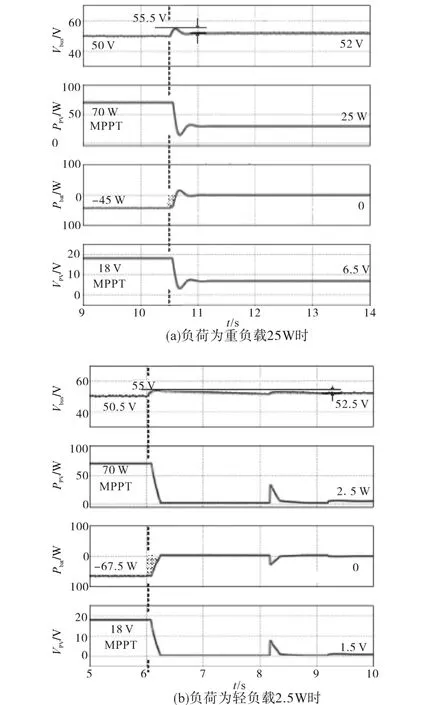
图9 含BES高功率滤波器补偿的PV-BES协调控制仿真结果Fig.9 Simulation results of PV-BES droop control coordination with BES HPF compensation

本文还通过实验验证了所提方法的有效性和优越性，实验装置如图10所示。PV模拟器用于模拟PV输出。转换器由TI F28379d DSP控制。参数设置同上述仿真系统相关参数。图11为不同BES HPF时间常数下PV-BES协调控制暂态实验结果。图11a中，BES HPF未激活或tHPF=0，PV切换到下垂控制的暂态过程中，直流母线电压有较大的过冲，与图8a的仿真结果一致。图11b中tHPF增大到0.01，在BES HPF补偿的帮助下，瞬态过程在3 V超调的情况下变得更加平滑。图11c中tHPF进一步增大到0.05，瞬态超调量进一步阻尼到2 V左右。由此可见，本文所提方法的电压调节性能良好。

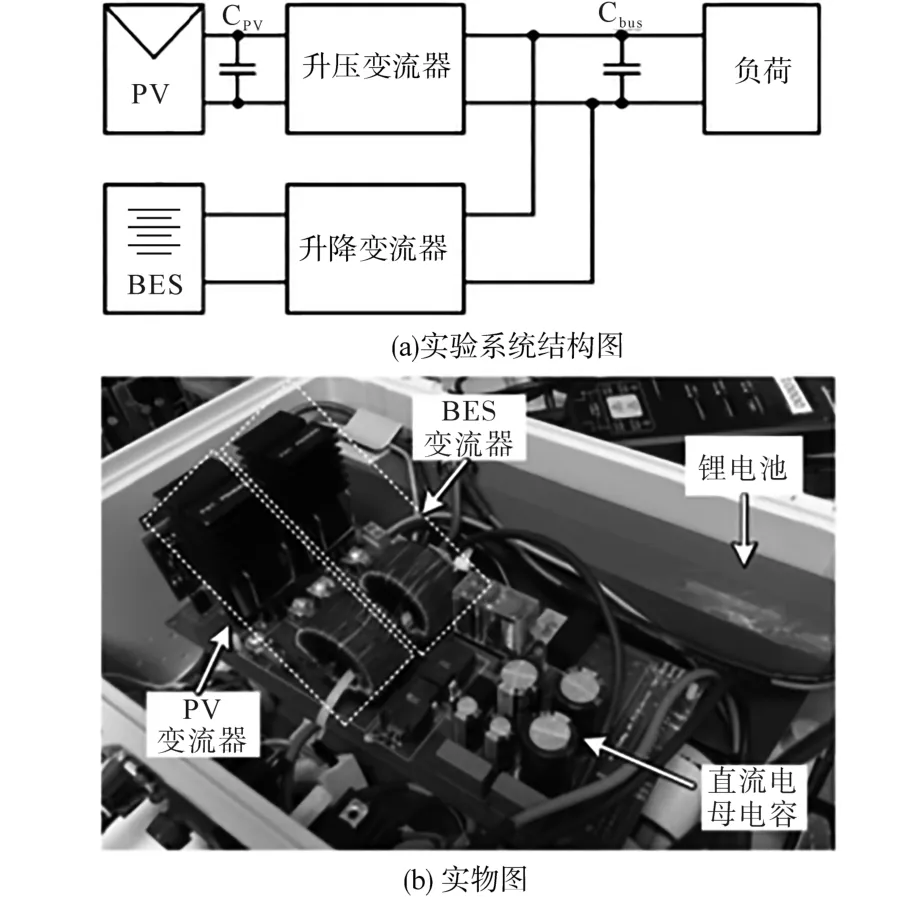
图10 实验系统图Fig.10 Experimental system diagram

图11 PV-BES协调控制实验结果（负荷为25W）Fig.11 Experimental results of PV-BES coordination control（load is 25W）

图12为2.5 W负载下PV控制模式由MPPT变为下垂控制的实验结果。超调量保持在2 V左右，波形与仿真结果如图9b所示吻合较好。

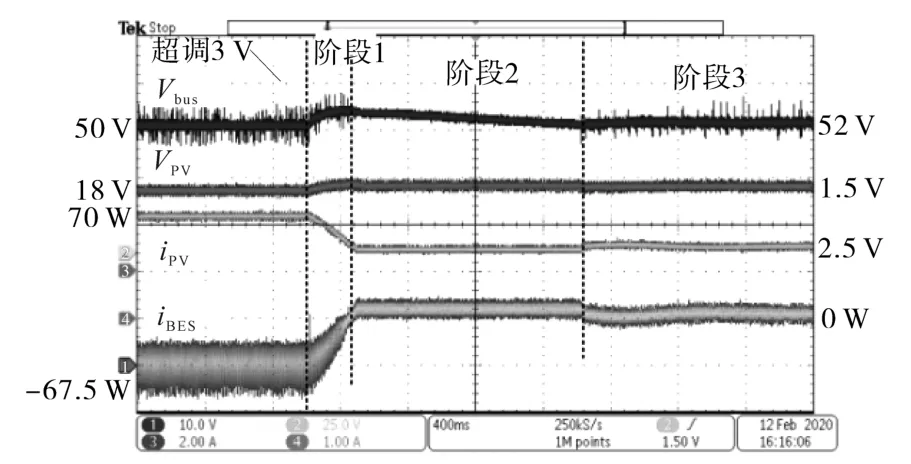
图12 PV-BES协调控制实验结果（负荷为2.5W）Fig.12 Experimental result of PV-BES coordination control（load is 2.5W）

从所有的结果可以看出，瞬态过程分为三个阶段（由于稳定时间较长，在图12中更加明显）。在第1阶段，BES完全充电，母线电压升高，由于HPF防止母线电压过冲，BES充电电流缓慢下降；在第2阶段，光伏输出功率降低到低于负载，母线电压降低。HPF通路将始终阻碍母线电压的变化。因此，在此阶段BES将会放电；第3阶段，母线电压降至下垂控制器设定的值，BES高频滤波器的输出趋于零，达到新的稳态。

4 结论

本文提出了一种PV-BES协调控制方法，克服了PV发电控制模式下母线电压调节的控制问题。整个控制方案保持了分散的、少通信的方式，可用于即插即用微电网（PnPMG）。所提出的方法利用了现有的BES系统，通过解耦控制回路，即使在发电控制模式下，BESs仍能提供动态补偿。最后，通过仿真和实验对本文所提方法进行了验证。