基于PCBN模型盾构下穿既有隧道施工安全风险评价
2021-11-11曾铁梅冯宗宝陈虹宇吴贤国
曾铁梅, 刘 茜, 冯宗宝, *, 陈虹宇, 吴贤国
(1. 武汉地铁集团有限公司, 湖北 武汉 430040; 2. 华中科技大学土木与水利工程学院, 湖北 武汉 430074; 3. 新加坡南洋理工大学土木工程与环境学院, 新加坡 639798)
0 引言
盾构隧道下穿既有隧道施工过程中极易诱发邻近既有隧道的变形,对盾构下穿既有隧道施工风险开展实时的安全评估与控制具有重要的工程意义。目前,国内外对于盾构下穿隧道的施工安全研究主要集中于数值模拟和模型试验等[1-2]。Khabbaz等[3]通过建立隧道施工与桩基相互作用的有限元模型,研究了在悉尼马丁广场下进行隧道施工的风险。Jallow等[4]利用PLAXIS 3D软件对台北捷运系统中某盾构隧道施工进行了有限元分析,探讨了盾构施工中引起隧道长期沉降的机制。何梦超等[5]基于模糊故障树模型,定量评估了地铁盾构隧道下穿既有轨道的风险大小。阿卜杜拉等[6]通过模型试验,针对既有隧道的应力变化,研究了盾构下穿对既有隧道的影响。王坚[7]结合理论分析和有限元数值仿真,研究了新建隧道盾构下穿既有隧道工程的影响。杨建烽等[8]通过模拟计算对盾构下穿既有地铁区间隧道的沉降控制进行了研究。张毫毫等[9]对新建隧道下穿施工对既有上卧盾构隧道扰动影响规律进行了研究。上述研究主要针对盾构下穿既有隧道施工的沉降变形进行分析,而很少从风险评估角度进行系统的安全评价与预警研究,且传统的评价方法没有考虑到盾构施工过程中风险的复杂性和模糊性,也难以反映多源因素间的相互作用。
本文将贝叶斯网络与Pair-Copula理论相结合,基于二者的优势提出基于PCBN模型的盾构下穿既有隧道施工风险评价方法,考虑多源风险因素之间复杂的相关关系,得到更加准确的风险评价模型,通过建立的PCBN模型进行风险分析及定性和定量相关性分析,实现工程施工风险的实时评估和关键的安全控制因素识别,为工程安全管理提供决策支持。
1 方法及原理
1.1 Pair-Copula理论
Copula理论是在Sklar定理的基础上发展而来的,能够对所选取随机变量之间的相关性进行描述,也称相依函数[10],其基本原理是采用某种映射将边缘分布函数联合成联合分布函数[11]。若f(x1,x2,…,xn)为节点X=(X1,X2,…,Xn)的联合分布密度函数,则在Copula函数的概念下,f(x1,x2,…,xn)可以被表示为:
f(x1,x2,…,xn)=f(x1)·f(x2|x1)·…·f(xn|x1,…,xn-1)。
(1)
在此思路下,将变量的各个边缘条件概率密度函数的Pair-Copula密度函数相乘便可得到变量的多元联合分布密度函数,具体思路为:
f(u|v)=Cuvj| v-j(F(u|vj),F(vj|v-j))·f(u|v-j)。
(2)
式中:v=(v1,…,vj,…,vd)为变量向量,其维度为d;vj(1≤j≤d)为从v中随意抽取的向量;将不包括vj的v定义为v-j,v-j=(v1,…,vj-1,vj+1,…,vd);Cuvj| v-j为Pair-Copula密度函数。
在此定义下,利用密度函数对分布函数进行还原,则有:
(3)
1.2 贝叶斯网络
贝叶斯网络通过有向无环图来反映具体问题中复杂变量之间的连接关系,是一种基于概率理论的网络模型,具有强大的不确定知识表达和推理能力[12]。对于贝叶斯网络中任意随机变量X=(xt1,xt2,…,xtn),相应的联合概率分布可以表示为:
(4)
式中:Xpa(tj)为随机变量X在时期tj的父结点集合;T为时期长度。
如果随机变量X为时间序列,且xti的父结点为(xtj-1,…,xt1),则式(4)可以转化为:
(5)
1.3 Pair-Copula贝叶斯(PCBN)模型
Kurowicka等[13]通过结合贝叶斯理论和Pair-Copula函数,引入了Pair-Copula Bayesian network这种改良的贝叶斯网络,并扩展了Copula理论的应用范围。令D=(V,E)表示一个BN对应的DAG,用Dm表示D的道德图,P为Rd的绝对连续概率测度,此概念下有D=|V|。在所有概率分布符合P特征的变量中,任意取一个变量X,假设P的概率密度函数为f,且P中的所有变量的边缘分布为F1,F2,…,Fd,基于上文所提到的Sklar定理可知,f可由F1,F2,…,Fd与相应的Copula函数C相乘来表示。
Bauer等通过研究与推理,发现C可由条件化下的许多Pair-Copula函数Cv,w|pa(v)来表示,在此概念中,v∈V,w∈pa(v)[14]。基于这个思路,贝叶斯概念下的网络结构D中的每个相关节点的箭线w→v都拥有一个条件化下的Pair-Copula,则f可表示成:

(Fv|pa(v;w)(xv|xpa(v;w)),Fw|pa(v;w)(xw|xpa(v;w)))。
(6)
式中x=(xv)v∈V∈Rd。
这种基于Pair-Copula函数的贝叶斯网络称为PCBN模型。
2 基于PCBN模型的施工风险评价
本文提出一种将贝叶斯网络和Pair-Copula函数相结合的盾构下穿既有隧道施工风险评价方法,对盾构下穿既有隧道进行实时有效的安全风险评估并为其提供决策支持,其评价流程如图1所示。

图1 基于PCBN模型的盾构隧道下穿既有隧道施工风险评价流程
2.1 评价指标体系建立
通过工程实践和相关文献分析,提炼出盾构下穿既有隧道安全风险的主要影响因素,包括隧道相关参数、土体条件、既有隧道条件、施工与管理因素4类,从而构建盾构下穿既有隧道安全评价指标体系[15]。
1)隧道相关参数: 新建隧道相关参数的设计是盾构隧道影响周围土体和构筑物非常重要的一类因素,它可以反映隧道开挖的大致情况。新建隧道相关参数一般主要考虑新建隧道的直径(X1)、两隧道的净距(X2)和两隧道的平面夹角(X3)3个参数[16-17]。
2)土体条件: 土体作为新建隧道与既有隧道相互作用的中间媒介,土体条件对于盾构隧道下穿引起既有隧道的变形破坏有着至关重要的作用[18]。其中,压缩模量(X4)、黏聚力(X5)、内摩擦角(X6)和泊松比(X7)是表征土体性质的几个常见影响因素。
3)既有隧道条件: 既有隧道的变形破坏与自身现有的条件有很大关系,既有隧道的埋深(X8)、既有隧道的直径(X9)和覆跨比(X10)会影响既有隧道的基底应力变化,从而影响隧道的变形[19]。既有隧道的健康状态(X11)则在一定程度上决定了隧道承受变形的能力。
4)施工与管理因素: 盾构隧道施工阶段,施工和管理因素对临近既有隧道安全的影响则主要体现在对盾构施工参数合理性的控制上[20]。具体来说,盾构施工参数主要包括注浆压力(X12)、土舱压力(X13)、推进力(X14)和推进速度(X15)等。
2.2 PCBN模型构建
2.2.1 最优边缘分布识别
边缘分布函数的作用是对变量的概率分布进行正确描述,其识别结果会直接影响风险评估的可靠性和准确性。本文选择Weibull函数、 Exponential函数、Normal函数和Gamma函数4种常用Copula函数作为备选函数,通过AIC准则和BIC准则2种方式来确定PCBN模型中风险指标的最优边缘分布函数,以保证风险指标分布函数选择结果的科学性。最优边缘分布函数即为使AIC值和BIC值最小时的分布,AIC准则和BIC准则的具体公式为:
(7)
(8)
(9)
式(7)—(9)中:x1i,x2i为2个随机变量;c(u1i,u2i)为分布函数的估计值;N为风险指标实测值的维度;k为Copula参数的个数,本文k取1。
2.2.2 PCBN模型设计
首先,根据专家知识和大量工程实践经验,将具有相关关系的风险指标用有向箭头连接,初步构建盾构隧道下穿既有隧道施工安全风险评价的有向无环图(DAG图),如图2所示;然后,基于实测数据计算具有相关关系的风险指标间的Spearman秩相关系数,见式(10);最后,根据计算的Spearman秩相关系数进行独立性检验,将相互独立的节点之间的箭头去除,从而对初步构建的DAG图进行修改和完善,并将各风险指标的最优边缘分布输入构建的DAG图中,从而构建盾构下穿既有隧道施工安全风险评价的PCBN模型。
(10)
式中:dk为2个变量之间的等级差,即本文中2个风险指标实测值的排序之差;z为等级差的个数,即风险指标实测值的维度。
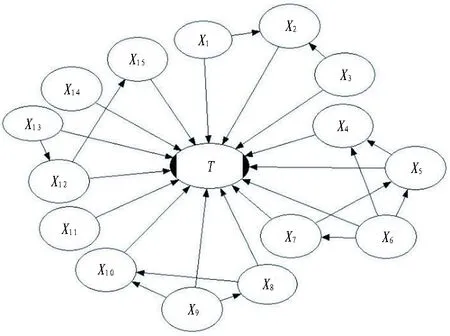
图2 初步DAG图
2.2.3 PCBN模型验证
为了保证PCBN模型的合理性,需要对模型的有效性进行验证。本文采用K-S检验对PCBN模型中单节点的边缘分布进行拟合优度检验,判断观测样本值和假设分布之间的差值是否符合设定的置信区间。给定一组长度为n的升序排列的样本数据为x( · ),则其K-S检验的统计量为:
T=sup|F*(x)-Fn(x)|。
(11)
式中:F*(x)和Fn(x)分别表示假设的分布函数和基于实测数据的分布函数; sup表示F*(x)和Fn(x)之间距离集的总和。
2.3 基于PCBN模型的风险分析
利用贝叶斯网络的概率推理技术,通过联合概率分布,可以直接推算出n个风险因素Xi(i=1,2,…,n)组合下风险事件T的发生概率,从而便于施工人员在事故发生前预判事故风险等级,以便及早采取控制措施。风险事件(即叶结点T)不同风险等级发生的概率可用P(T=t)(t=1,2,…,5)表示,其计算公式为:
P(T=t)=P(T=t|X1=x1,X2=x2,…,Xn=xn)×
P(X1=x1,X2=x2,…,Xn=xn)。
(12)

2.4 基于PCBN模型的指标相关性分析
PCBN模型可以进行参数相依性的准确识别和高精度重构,基于所构建的PCBN模型进行基于百分位蛛网图[21]和相关系数的相关性分析,可以定性和定量地判断风险系统中与盾构下穿既有隧道施工风险相关性较大的风险因素,即为关键风险因素,并依据相关性大小确定决策的优先权,明确盾构下穿既有隧道风险管理的重点管理环节与检查点。
3 案例分析
3.1 工程概况
武汉市地铁8号线一期工程总长16.7 km,共设有12个站点,中间贯穿了永清商务区、徐东商业区、街道口商业区等经济带,是连接长江两岸的一条重要交通线路。8号线一期工程采用土压平衡盾构施工,在宏图大道站至塔子湖站区间内下穿地铁3号线,与3号线在金银潭大道和宏图大道的路口相交,相交后沿宏图大道并行约200 m。在该区段设置100个监测点,获得100组监测数据,如表1所示。
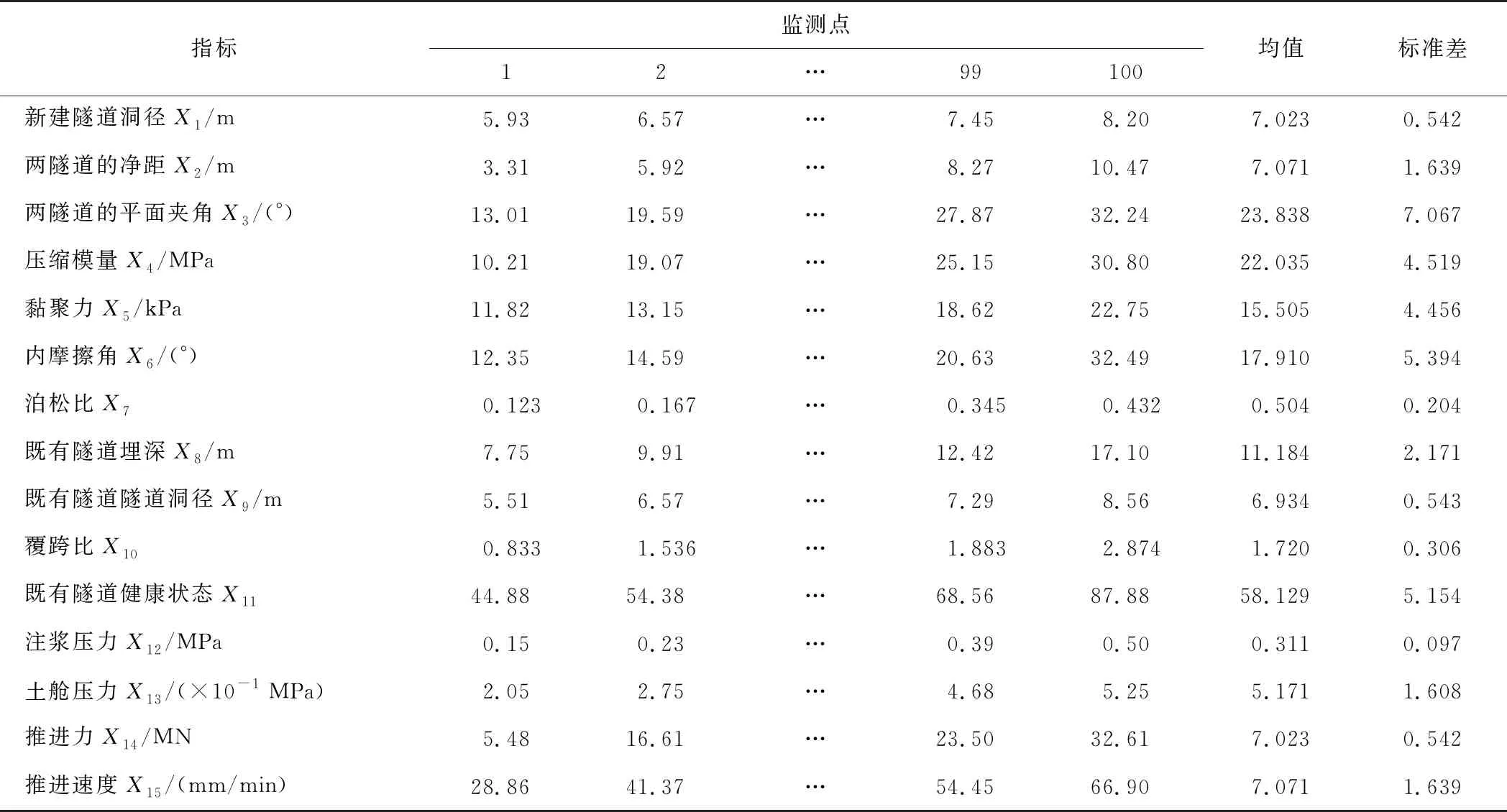
表1 隧道相交区间段监测数据
3.2 PCBN模型构建
3.2.1 最优边缘分布识别与检验
基于表1中15个风险指标的实测值,在归一化处理后,根据式(7)—(9)进行最优边缘分布函数识别,并根据式(11)对各风险指标识别拟合结果进行K-S检验。设定显著水平α=0.05,若统计量P值大于显著性水平0.05,则假定的边缘分布拟合;反之,假定的边缘分布不拟合。计算得到各指标最优边缘分布K-S检验的拟合优度均较好。部分指标识别和检验结果如表2所示。
3.2.2 贝叶斯网络结构设计
首先,将施工风险评价指标体系中的15个风险因子作为贝叶斯网络DAG图的节点,结合专家经验和相关文献资料,初步构建出风险评价的DAG图。然后,根据式(10)进行独立性假设检验,对初步DAG图进行修剪和完善。设定显著性水平为0.1,若P值大于0.1,则两节点为独立关系,否则两节点间存在一定程度的相关关系。节点之间独立性检验结果显示X3和X2、X9和X8、X13和X12之间相互独立,则剔除其经验相关关系,修剪完善后的DAG图见图3。
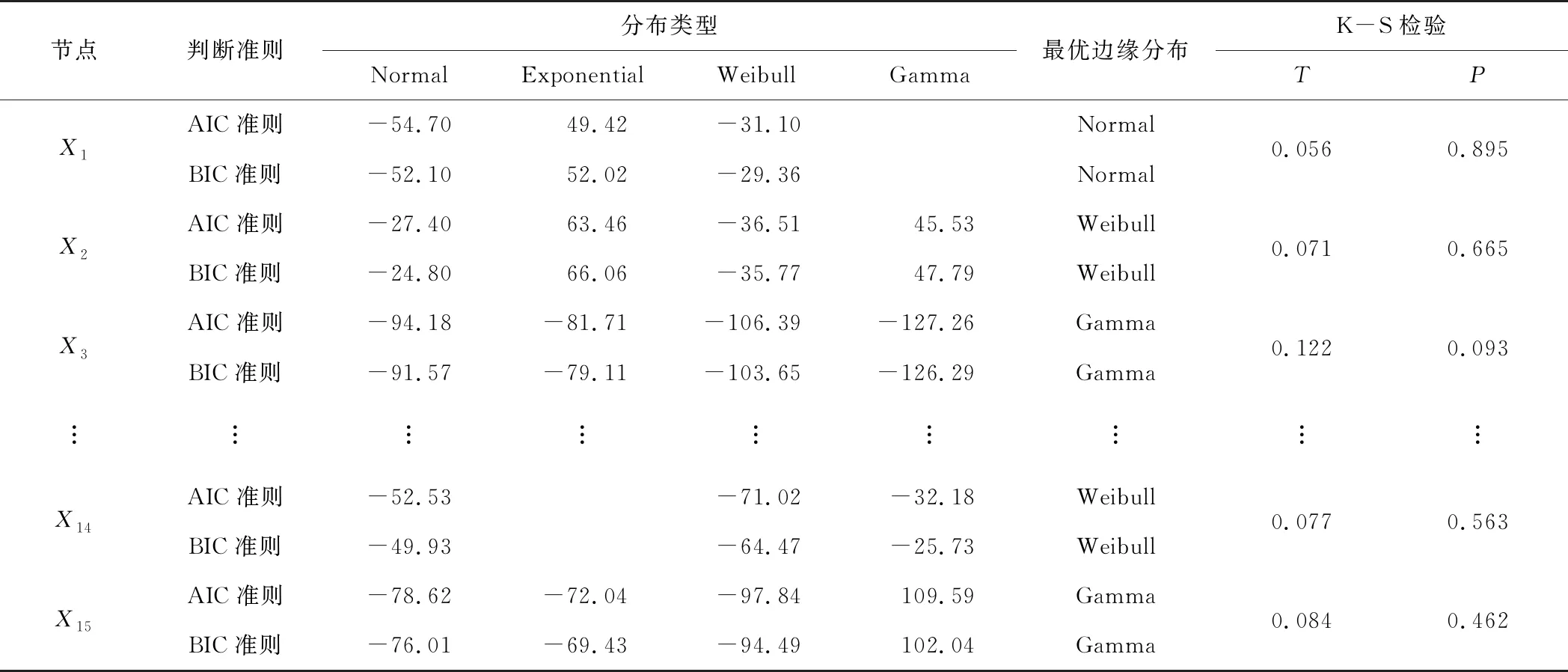
表2 AIC和BIC准则的最优边缘分布函数及拟合优度K-S检验结果

图3 调整完善后的风险系统PCBN网络DAG设计图
3.3 基于PCBN模型的风险分析
基于构建的PCBN模型,结合工程实际与专家经验,可将该工程的安全风险划分为5个安全状态,对应5个风险等级,各个风险等级与工程风险区间值的对应关系如表3所示。

表3 工程风险等级标准
根据式(12),通过各节点的分布参数及各个节点之间的相关系数进行风险值推理,得到盾构下穿既有隧道施工风险值,绘制出该工程盾构下穿既有隧道施工风险评价的PCBN模型,如图4所示。

图4 盾构隧道下穿既有隧道施工风险PCBN模型图
由图4可知,该工程施工过程的风险值均值计算结果E(T)=0.387,标准差计算结果为0.071 9,故该工程施工风险值范围为[0.315 1,0.458 9]。依据表3可以判断该工程盾构下穿既有隧道施工风险等级为Ⅲ级,即该工程施工风险状态为基本安全。但是,由于在Ⅲ级风险值范围内,该工程的风险值偏高,有向Ⅳ级较危险状态发展的趋势,因此,可以判断某些监测点或者该隧道的某些风险指标的风险等级状态较高。为了对盾构下穿既有隧道施工风险进行管理与控制,应当进一步确定关键致险因子。
3.4 基于PCBN模型的指标相关性分析
基于PCBN模型进行定性和定量的相关性分析,确定相关性大的因素为关键致险因子,为盾构下穿既有隧道施工风险控制提供依据。
3.4.1 百分位蛛网图分析
百分位蛛网图通过多个样本有效反映了PCBN模型中各个风险指标与施工风险之间取值的相关关系,通过条件化蛛网图,即设定施工风险值的取值区间,即可观察条件化下各个风险指标的取值情况,从而定性地确定风险系统中与工程施工风险变化相关性较大的风险指标。图5为盾构下穿既有隧道条件化的风险蛛网图。由图可以看出,在T高概率值和低概率值的条件化下,指标X12、X14、X15的蓝色样本线条(T的高概率值)分布基本集中于纵轴上部,黑色样本线条(T的低概率值)基本集中于纵轴下部。这表明,在该工程风险系统中,指标X12、X14、X15与风险变量T的高概率值和低概率值具有较强的相关关系,这3个因素对风险变量T的风险等级的影响更大。故注浆压力(X12)、推进力(X14)、推进速度(X15)为影响本工程施工风险的重要指标,当盾构隧道下穿既有隧道施工过程的风险较高时,应首先对这3个风险指标采取控制措施。

图5 盾构隧道下穿既有隧道条件化的风险蛛网图
3.4.2 相关系数分析
相关系数能够定量反映致险因子与施工风险之间的相关程度,从而判断对施工风险影响较大的关键因素。本文选用Pearson相关系数和Spearman相关系数分别度量Xi与T之间的线性和非线性相关关系。一般相关系数大于0.5时认为具有显著相关性,当相关系数为0.3~0.5时,认为具有中等相关性。基于构建的PCBN模型,计算15个风险指标关于工程施工风险T的Pearson相关系数和Spearman相关系数,结果如图6所示。

图6 指标Xi关于施工风险T的相关系数
由图6可知,在风险系统的15个风险指标中,X15、X14、X123个指标的相关系数值最大。X15与工程施工风险的线性相关系数和非线性相关系数均大于0.5,表明X15与工程施工风险之间呈显著相关;X14与工程施工风险的线性关系为显著相关,非线性关系为中等相关;X12与工程施工风险的线性关系和非线性关系均为中等相关。因此,本工程中推进速度(X15)为对盾构下穿既有隧道施工风险影响最大的风险指标,推进力(X14)和注浆压力(X12)为影响次之的2个风险指标,它们3个指标是本工程风险系统中的关键风险指标,该分析结果与通过蛛网图定性分析所获得的结论一致。根据所识别出的关键风险指标,可以采取一定的风险预控应对措施。在施工过程中,应当重视对主要因素X12、X14、X15的监测和检查,当施工风险过高时,首先考虑推进速度、推进力和注浆压力的参数是否在正常范围,并对盾构推进系统、注浆系统进行检查,及时进行检修调控,从而降低工程施工风险。
4 结论与讨论
本文在贝叶斯网络的基础上引入Pair-Copula理论,提出了一套基于PCBN模型的风险评价方法,在模型中通过不确定推理确定施工风险等级,又通过相关性分析识别关键致险因素,实现了盾构下穿既有隧道施工过程的安全风险评价。以武汉某隧道下穿工程为背景进行实例研究,主要结论与讨论如下:
1)基于实测数据,利用提出的PCBN模型进行风险分析,确定该隧道工程的施工风险等级为Ⅲ级,施工风险状态为基本安全,但有向较危险状态发展的趋势。
2)该工程施工风险系统中的关键风险指标为注浆压力(X12)、推进力(X14)和推进速度(X15),为盾构下穿既有隧道施工风险管理提供了依据。
3)本研究仅在二维空间下,利用PCBN模型对于两两节点之间的相关性进行了分析,在未来的工作中,可以研究3个及以上节点的相关性,探究多维空间下系统内部的相依性关系,实现更科学的决策与管理。
