优化GA-BP神经网络模型及基坑变形预测
2021-11-11李峰辉刘秀秀
刘 锦, 李峰辉, 刘秀秀
(1. 陕西铁路工程职业技术学院城轨工程学院, 陕西 渭南 714000;2. 郑州市交通规划勘察设计研究院, 河南 郑州 450000; 3. 曲阜远东职业技术学院, 山东 济宁 273100)
0 引言
基坑工程影响因素多、施工难度大,工程建设风险随开挖规模扩大急剧增加[1]。坑内土体因开挖卸荷形成内外压力差,支护结构内力改变产生位移形变;若结构强度或刚度不足,易导致支护桩倾斜,发生土体坍塌事故,严重时会造成地坪开裂、管线损坏及周围建筑物不均匀沉降[2]。因此,对基坑开挖实施动态监测尤为重要。根据监测数据适时调整施工工艺和支护参数,可实现信息化施工,保证基坑尽可能在安全经济的环境下进行施工。
传统基坑监测方法忽视位移形变的预警,仅事后采取补救措施,错失加固修复最佳时机,存在重大安全隐患。基坑变形随时间呈不规则非线性演化,位移值属于非平稳的复杂时间序列,因而具有优越的非线性动态处理能力的BP(back propagation,简称BP)神经网络被广泛用于基坑变形预测。目前,许多学者依托实际工程构建多种BP神经网络模型用于基坑变形预测。张庆华等[3]提出“新陈代谢”方法选取人工神经网络模型训练样本,能有效预测基坑的长期变形; 杨茜[4]通过对比优选网络训练模式和传递函数,改进模型对隧道结构整体沉降预测效果良好; 胡启晨等[5]建立BP神经网络预测模型用于基坑开挖变形预测,具有一定应用价值; 谭儒蛟等[6]基于神经网络提出一种土体参数反演方法; 刘聪等[7]从基坑变形影响因素分析输入层神经元结构,并结合工程实例进行预测分析。
BP算法因自身传递函数限制,导致其存在收敛速度慢、易陷入局部极小点的缺陷,引入具有强大的全局寻优能力的遗传算法可在一定程度上有效克服其不足。利用遗传算法随机性和全局性特点,李彦杰等[8]基于遗传算法对BP算法的初始权重和阈值进行改进,建立的预测程序对深基坑地下连续墙围护结构水平位移预测准确度高; 周星勇等[9]针对BP神经网络存在的过度拟合和局部最优的缺点,引入自适应增强算法对遗传神经网络预测模型进行改进; 胡圣武[10]用遗传算法对灰色神经网络进行改进,提高了预测精度; 宋楚平[11]利用遗传算法对模型权重初值进行优选,改进模型的收敛速度和泛化能力均得到提升。
上述预测模型对基坑变形具有一定参考价值,但在训练样本选取、样本数据预处理及隐含层结构设计等方面仍存在优化空间,模型的预测精度和运算速度有待进一步提高。为解决上述问题,本文对GA-BP模型的归一化区间和隐含层结构进行深入优化,并对实际工程基坑支护桩体测斜位移展开预测,通过误差分析验证预测模型的合理性和优化效果,以期进一步为基坑变形监测提供理论依据。
1 GA-BP神经网络
1.1 BP神经网络
BP神经网络理论以人脑的自组织、自适应及容错性为模拟对象,通过BP算法对实测资料进行自身训练和规则学习,高效解决有关问题。模型由输入层、隐含层及输出层构成,各层可根据需要扩展成多层,邻近层以权重和阈值连接并借助传递函数承担信号的转化与传播任务,属于多层前馈性神经网络,网络拓扑结构如图1所示。图中:x1,x2,…,xi-1,xi表示初始输入数据;w1,w2,…,wi-1,wi和α1,α2,…,αi-1,αi分别表示输入层权值和阈值;γ1,γ2,…,γj-1,γj和β1,β2,…,βj-1,βj分别表示隐含层权值和阈值;i和G分别表示输入值和输出值。
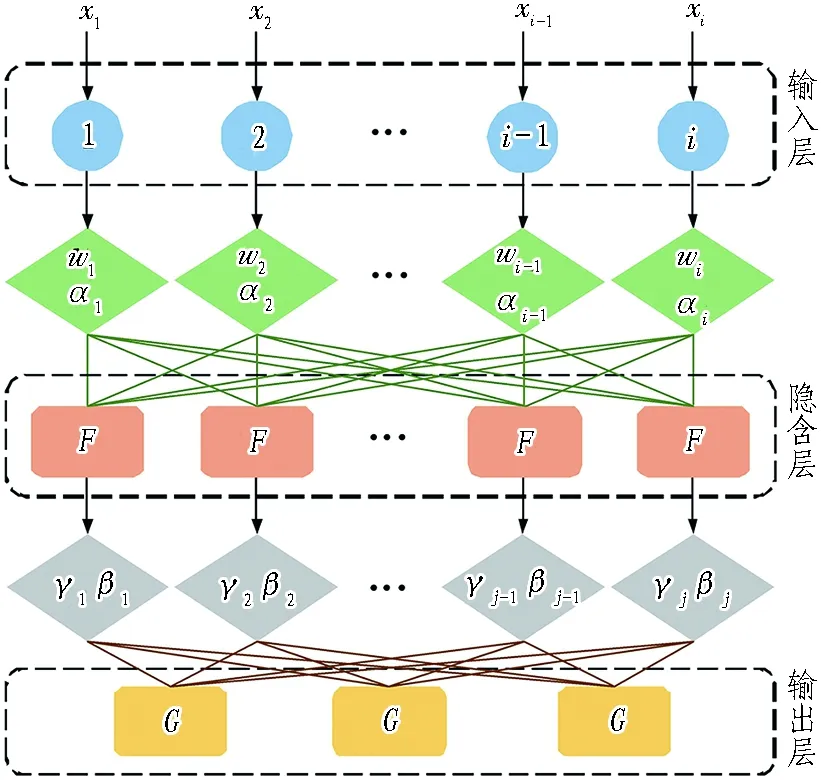
图1 BP神经网络模型拓扑结构图
BP神经网络独特的无监督学习算法是实现其功能的核心,利用梯度下降法校正输出结果误差平方和的误差反向传输,是保证预测结果精度的前提。学习算法流程主要由信号顺向传播、误差反向传输及循环训练与判别收敛等3个阶段构成。
1.2 遗传算法优化流程
遗传算法(genetic algorithm,简称GA)是一种结合Darwin适者生存进化论和Mendel基因遗传机制形成的具备全局最优搜索能力的算法,目的在于实现BP神经网络各层连接权值和阈值的最优化,摆脱BP算法对梯度信息的过度依赖。
GA算法优化基本思路是: 将初始权重和阈值编码完成种群初始化,确定个体筛选标准—适应度,利用遗传算法的选择、交叉及变异操作对群体进行淘汰选优,最终获得神经网络最佳连接权值和阈值,其详细算法流程如图2所示。

图2 GA-BP神经网络模型算法流程图
2 GA-BP神经网络预测模型优化
2.1 样本数据预处理方法的优化
神经网络训练需对实测数据进行归一化处理,即将原始数据映射至选定的归一化区间,据此可将有量纲的原始数据转变成纯数值的标量,在提高模型训练速度和灵敏度的同时,有效预防陷入S型传递函数的饱和区。因此,归一化区间的范围对于神经网络模型的性能具有重要影响。
为寻求GA-BP神经网络模型的最佳归一化区间,利用MATLAB神经网络工具箱中的Postreg函数,对采取不同归一化区间进行归一化处理的模型开展训练效果回归分析验证,以相关参数R(即网络输出与目标输出的相关系数)表征各归一化区间的训练质量,其中R值越接近于1,表明网络输出与目标输出越接近,网络的性能越好,具体分析结果如图3所示。由图可知,采用不同归一化区间网络模型的训练效果离散性较大,最佳归一化区间为[0.05, 0.95]。
2.2 隐含层结构优化
神经网络模型输入层和输出层结构由预测对象的训练样本和需求结果共同决定,因而中间隐含层的构成及其含有的神经元节点数将直接影响模型的学习能力和运算处理水平。需要注意的是,节点过少会造成模型容错性差,导致识别训练样本的能力降低,而节点过多则引起学习算法的运行时间显著增长,降低实际工程应用价值。因此,模型的隐含层结构需根据具体情况适当调整。

注: 横坐标值表示归一化区间左端点,x表示归一化区间左端点值。
2.2.1 单隐含层及神经元个数
现有神经网络预测模型多采用单隐含层结构,参考相关工程实例[3-9,11-15],隐含层神经元个数与输入层神经元个数的关系如图4所示。

图4 隐含层神经元个数与输入层神经元个数关系
利用最小二乘法对上述数据进行曲线拟合,可得单隐含层最佳神经元个数与输入神经元个数的关系,可见单隐含层节点数最佳区间为[4,7],单隐含层能够包含的节点数受模型自身限制,显然无法满足输入神经元个数较多的工况。
2.2.2 双隐含层及神经元个数
采用实测数据作为训练样本代入预测模型,即输入神经元个数较多时,单隐含层结构由于包含的神经元个数过多,将显著降低网络训练效果和模型预测精度。
参考相关方法[4]和数据[13]分别开展GA-BP神经网络的单、双隐含层训练,训练效果如图5所示。

图5 单、双隐含层训练效果图
由图5可知,双隐含层结构达到预期目标误差的循环迭代次数均小于单隐层结构,说明当输入层节点数较多时,采用双隐含层结构的神经网络模型的训练效果远比单隐含层结构的好。
部分训练程序代码如下:
[Pn,minp,maxp,Tn,mint,maxt]=premnmx(P,T);
[kn,ks]=mapminmax(k);
[fn,fs]=mapminmax(f);
p=Pn;t=Tn;
net=newff(minmax(P),[a,b],{‘tansig’,‘purelin’});
net.trainParam.show=x1;
net.trainParam.epochs=x2;
net.trainParam.goal=x3;
net.trainParam.lr=x4;
[net,tr]=train(net,Pn,Tn);p,t。
其中,P和T是样本归一化后训练样本的输入和输出,[a,b]、x1、x2、x3、x4均为适时调整参数。
3 改进模型的建立
3.1 输入层与输出层设计
基坑施工环境是动态变化的,因此,沉降变形具有“时空效应”,运用前期实测数据预测下一阶段变形情况,可显著降低人为因素干扰和施工环境差异引起的误差。本文用连续4次的变形数据预测第5次位移值,故输入层神经元共4个,输出层表示该测点4+id的沉降参数,即含有1个神经元。
3.2 隐含层
输入神经元个数大于4时,采用双隐含层结构可有效防止函数溢出,提高模型预测结果的速度和精度,且可根据需要实时增加样本数据,实现基坑变形的实时动态监测。经试算确定隐含层的神经元个数分别为7、8,因此,本文GA-BP预测模型的网络结构为“4—2(7,8)—1”。
3.3 训练样本选取与数据预处理
部分学者以基坑变形影响因素作为训练样本[11,14],但由于各因素间关系错综复杂,难以准确把握最关键因素,且部分指标无法量化,导致建立的模型与实际情况匹配度低,预测结果与期望值相比误差过大。因此,本文采用基坑变形实测数据作为模型输入量,在有效降低人为因素干扰的同时能够显著降低施工环境差异引起的误差,从而较好地反映系统的内在变形规律,预测结果可以更好地应用于工程实践。同时,鉴于施工初始阶段监测数据少,无法满足样本需求,通过“新陈代谢”的方式控制训练样本,将施工期间的监测数据实时添加至样本中,在提高模型预测精度的同时实现动态监控。
将选取的训练样本进一步归一化预处理至[0.05, 0.95],计算过程如式(1)所示。
(1)

归一化与反归一化MATLAB实现程序语言如下:
输入训练样本p和训练输出样本t
fori= 1:n;
P(i,:)=0.9*(p(i, :)-min(p(i, :)))/(max(p(i, :))-min(p(i, :)))+0.05;
T(i,:)=0.9*(t(i, :)-min(t(i, :)))/(max(t(i, :))-min(t(i, :)))+0.05。
最后,MATLAB软件要将训练样本的输出值和预测样本的输出值都进行反归一化:
y=(Y(1,:)-0.05)*(max(t)-min(t)/0.9+min(t);
yt=(Yt-0.05)*(max(t)-min(t))/0.9+min(t)。
其中,Y为训练样本输出值,Yt为预测样本输出值。
4 工程实例预测
4.1 工程概况
某人防工程拟建场地邻近交通要道及市政排污管道密集区域,北侧15 m为地下车库工程基坑,西北侧为重要历史建筑保护范围。基坑平面呈不规则多边形,总面积约22 000 m2,挖土深度为7.70~11.60 m,基坑上部4.0 m采用土钉支护,下部为桩锚支护,基坑周边采用高压旋注浆形成的水泥墙作为止水帷幕,安全等级为一级。西侧有临时道路,在地面1.2 m以下采用桩锚支护,上部1.2 m在冠梁上砌筑砖墙作为支护结构。在基坑周边共布设8个测斜管,选取CX-6号测斜管的监测数据进行支护桩位移预测。对基坑变形安全进行监测,可及时掌握支护结构受力和变位情况,保证项目施工处于安全经济的状况下运行,基坑平面及测斜管布置如图6所示。

图6 基坑平面及测斜管布置示意图
4.2 模型优化效果验证
为验证GA-BP模型优化效果,将优化GA-BP神经网络的预测结果与未改进的BP和GA-BP神经网络模型进行对比分析,通过相对误差表征预测效果优劣,结果如图7所示。

图7 模型预测效果对比
由图7可知, 优化GA-BP神经网络模型的残差值及其波动性明显优于常规BP模型和未经优化处理的GA-BP模型,进一步验证了本文模型具有更好的预测精度和可靠性。
4.3 模型合理性验证及误差分析
CX-6测斜管不同深度处的水平位移随时间的变化曲线如图8所示。由图可以看出,位移整体随时间增长呈3阶段变化,即快速增长阶段Ⅰ、稳定发育阶段Ⅱ、缓慢变形阶段Ⅲ; 变形幅度与测斜深度呈反比; 测斜变形增长速率逐渐趋于缓和,在50 d之后基本保持稳定。

图8 CX-6测斜管不同深度处的水平位移随时间的变化曲线
经过反复试运行确定单隐层最佳神经元个数区间为[4,7],此时模型循环收敛速度快,运行误差小,预测精度高。
选取时间0 ~ 40 d共40组数据作为训练样本,迭代计算达到预期设定误差后,对41~50 d对应CX-6测斜管不同深度(2.0~4.5 m)的水平位移进行预测,其实测与预测结果对比如图9所示。
由图9可知,预测曲线与实测值相比吻合度高,由于基坑开挖过程中施工环境动态变化且次要影响因素被忽略,导致预测值普遍略小于实测值; 同时,变形趋势具有时间记忆特性,模型对时间点接近训练样本的位移预测值精度更高,二者差值随时间增长逐渐变大。因此,实际应用时需要不断更新训练样本以提高长期预测的精度和可信度,工程实践中可据此掌握基坑不同深度的变形情况,相应采取不同的加固预防措施,有效防止工程事故的发生,实现信息化动态施工监测。
通过精度评价指标(绝对误差区间宽窄、相对误差分布状态)对预测值进行误差分析,评判预测效果,不同深度下的水平位移误差情况如图10所示。
由图10可以看出,整体上各深度的位移预测值偏差均保持在0.2 mm以内,绝对误差区间宽度为0.07 mm; 最大相对误差为4.0 m深度处的1.35%,显然满足施工安全要求,能够为工程施工提供准确的参考依据。
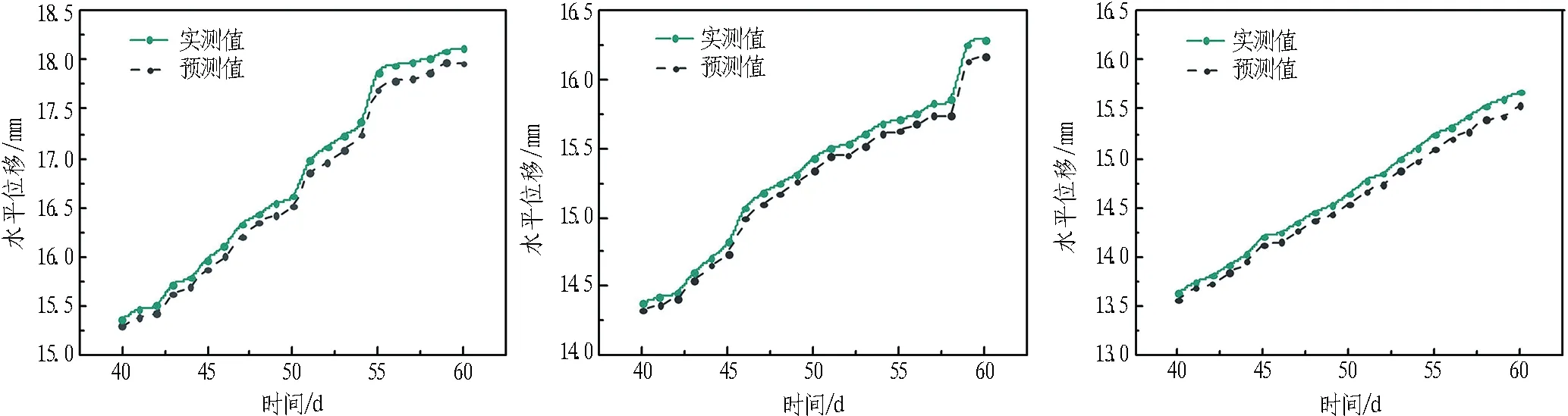
(a) 2.0 m深度 (b) 2.5 m深度 (c) 3.0 m深度

(d) 3.5 m深度 (e) 4.0 m深度 (f) 5.0 m深度
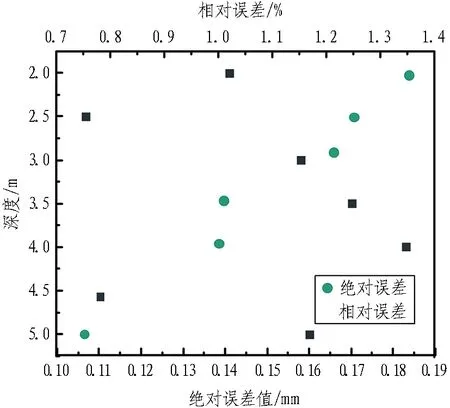
图10 不同深度下的水平位移预测误差分布
5 结论与建议
针对现有GA-BP神经网络预测模型在训练样本预处理和隐含层结构设计方面的不足,提出进一步优化方法,主要结论如下:
1)基坑变形随时间呈不规则非线性演化,具有强大全局寻优能力的遗传算法可有效克服BP算法收敛速度慢、易陷入局部极小点的缺陷,显著提高神经网络模型的收敛速度和泛化能力。
2)基坑变形“时空效应”显著,通过“新陈代谢”方式选取训练样本可显著降低人为因素干扰,相关系数回归分析验证样本预处理的最佳归一化区间为[0.05, 0.95];单隐含层的最佳神经元个数区间为[4,7],双隐含层结构适用于输入神经元个数较多情况,可根据需要实时添加监测数据,防止函数溢出,有助于提高预测结果的速度和精度。
3)基坑测斜管位移随时间增长呈快速增长、稳定发育、缓慢变形等3阶段变化,变形趋势具有时间记忆性; 精度评价指标符合安全施工需要,可实现动态化施工监测,经多模型对比可知模型优化效果良好。
目前仅对GA-BP神经网络模型进行双隐含层结构设计,后续能否采用三或四隐含层结构有待进一步研究,以提高神经网络模型的运算速度和预测精度。
