深中通道钢壳沉管自密实混凝土拌合物泵后性能评价及预测模型研究
2021-11-11宋神友陈文广徐金俊赵家琦范志宏
宋神友, 于 方, 陈文广, 徐金俊, *, 赵家琦, 范志宏
(1. 深中通道管理中心, 广东 中山 528400; 2. 中交四航工程研究院有限公司, 广东 广州 510230; 3. 南京工业大学土木工程学院, 江苏 南京 211816)
0 引言
深中通道是集“超大跨桥梁-人工岛-海底沉管隧道-水下互通立交”于一体的世界级超大型工程,行车规模采用双向8车道技术标准,隧道段全长6 845 m,其中沉管段长5 035 m,由32节管节(E1—E32)和1个最终接头组成。沉管采用2孔1管廊式的钢壳混凝土管节结构,此类结构不仅具有良好的承载和变形能力、防水和施工性能,而且兼具良好的经济效益[1-2]。深中通道钢壳沉管因其“超大、变宽、深埋、回淤大”等特点,工程建设的难度堪称世界之最[3-5]。
自密实混凝土因其优良的填充性、间隙通过性和抗离析性能,被广泛应用于各类工程中[6-8]。深中通道工程沉管段采用钢壳自密实混凝土结构预制,因自密实混凝土泵后质量直接影响钢壳沉管的预制质量(舱格填充的密实性), 若泵送过程质量控制不好,会直接影响到混凝土的施工性能和受力性能[9]。鉴于此,工程现场采用对自密实混凝土拌合物的泵后性能进行严格质量控制措施来保证沉管的预制质量。因自密实混凝土性能测试频率较高,测试工作量较大,若能建立准确的泵后性能预测模型,则可仅通过对自密实混凝土拌合物泵后性能进行控制实现钢壳沉管的质量控制。值得注意的是,自密实混凝土拌合物泵后性能受环境温度、混凝土输送时间、泵送距离和弯头数量等多种因素的影响,这对泵后自密实混凝土拌合物性能的预测带来了不小的挑战。
目前,国内外关于实体工程中对自密实混凝土温度、输送时间、泵送距离和弯头数量的影响研究很少。已有的研究主要集中于模拟试验方面,例如: 通过模拟试验来研究长距离泵送对自密实混凝土拌合物泵送前后性能的影响[10]; 研究环境温度对自密实混凝土扩展度经时变化的影响[11]。关于性能预测模型的研究主要集中于采用神经网络模型的研究方面[12],未见有关在温度、时间、泵送距离和弯头数量等多因素影响下的自密实混凝土拌合物性能预测模型的研究。因此,建立多种因素影响作用下自密实混凝土拌合物的性能预测模型,实现钢壳沉管自密实混凝土质量的精准控制,是需要解决的关键问题。
机器学习和贝叶斯概率模型因其强大的数值功能在土木工程中得到了广泛应用[13-16]。本文利用深中通道工程E1—E4节段实体工程自密实混凝土拌合物泵后性能实测数据,基于灰色关联理论分析入模温度、输送时间、泵送距离和弯头数量多种因素耦合下自密实混凝土拌合物泵后性能的影响规律,确定各因素的影响权重,并进一步采用支持向量机和贝叶斯推断等手段,分别建立泵后性能的隐式和显式预测模型,同时利用实体工程泵送过程数据对模型的准确度进行额外验证。
1 原材料及试验方法
1.1 混凝土原材料与配合比
深中通道钢壳沉管管节均采用C50强度等级的自密实混凝土。原材料及主要指标如下:
1)水泥。英德海螺水泥有限公司,P·Ⅱ42.5水泥,密度为3.11 g/cm3,比表面积为342 m2/kg。
2)粉煤灰。中国国电集团公司谏壁发电厂,F类Ⅰ级粉煤灰,密度为2.53 g/cm3, 细度(45 μm方孔筛筛余)为9.8%。
3)矿粉。唐山曹妃甸盾石新型建材有限公司,S95级,密度为2.90 g/cm3,比表面积为406 m2/kg,7 d活性指数为76%,28 d活性指数为102%。
4)砂。青莲镇Ⅱ标段河砂,细度模数为2.8,含泥量为0.3%,泥块含量为0。
5)碎石。中山明耀石场,5~10 mm和10~20 mm碎石,含泥量为0.2%,泥块含量为0,针片状含量为1.0%,压碎指标为4.0%。
6)水。饮用水。
7)减水剂。江苏苏博特新材料股份有限公司,聚羧酸高性能减水剂(酯类),含固量为17.8%,减水率为31%(掺量1.0%)。自密实混凝土配合比如表1所示。

表1 自密实混凝土配合比
1.2 拌合物性能测试方法
自密实混凝土的含气量、坍落扩展度、V漏斗时间、L型仪H2/H1分别参照GB/T 50080—2016《普通混凝土拌合物性能试验方法标准》、JGJ/T 283—2012《自密实混凝土应用技术规程》、CECS 203—2006《自密实混凝土应用技术规程》、CECS 02—2004《自密实混凝土设计与施工指南》进行测定。
1.3 试验数据库
通过现场试验共获得了150组实测数据,均来自深中通道E1—E4管节自密实混凝土现场浇筑取样测试结果。综合考虑泵送距离、弯头数量、输送时间以及环境温度对混凝土拌合物泵后性能的影响(输送时间包括混凝土自出站后至泵送地点的运输时间、到达泵送地点至开始泵送的等待时间以及开始泵送至从泵管中泵出的运动时间)。需要注意的是,泵送距离、弯头数量、输送时间及环境温度实测分别为32~155 m、4~10个、10~69 s及18~25 ℃。为了考察自密实混凝土拌合物的泵后性能,以泵送混凝土拌合物的入模温度、扩展度、V漏斗流动时间、L型仪H2/H1及含气量作为评价指标,进而建立自密实混凝土拌合物泵后性能与关键影响参数(泵送距离、弯头数量、输送时间、环境温度)之间的内在联系,构建相应的试验数据库。自密实混凝土拌合物泵后性能的统计分布如图1所示。

(a) 入模温度 (b) 扩展度 (c) V漏斗流动时间

(d) L型仪H2/H1 (e) 含气量
自密实混凝土拌合物性能在泵送过程会有损失,具体表现为工作性损失(扩展度、V漏斗流动时间减小),而入模温度和含气量均提高。这主要是由于泵送过程中,常伴随着自由水或浆水的泵出,同时水泥水化会消耗水泥浆体内的自由水,进而导致泵出后的混凝土拌合物浆水不足,最终造成混凝土工作性经时损失、混凝土入模温度和含气量提高以及屈服应力增加[17]。若泵送距离过大或者弯头数量过多,泵后混凝土拌合物则基本失去流动性,甚至还会出现堵泵现象;此外,泵管内的混凝土常常处于高剪切应力状态,混凝土均匀性被极大地削弱,这也会降低其流动性。可见,采用现场质量控制的方法对自密实混凝土的泵送过程进行检测必不可少,对混凝土拌合物的泵送后性能进行预测具有重大工程意义。通过分析泵送混凝土拌合物泵送后性能,可以实现对原材料、配合比、运输车辆和施工工艺的合理调控,保障出机后自密实混凝土的工作性能满足实际施工的需要。
2 灰色关联分析
灰色关联分析方法的特点是对一小组统计样本进行定量评价,通过判断研究对象之间的影响程度快速掌握特定参数与目标性能之间的相关性[18]。在本次评估中,考虑以泵送距离、弯头数量、输送时间和环境温度为变化参数并将其选为灰色关联系统的子序列{xi(j)},相应地定义为比较矩阵Xi(j); 以自密实混凝土拌合物的泵后性能(入模温度、扩展度、V漏斗流动时间、L型仪H2/H1、含气量)作为灰色关联系统的母序列{x0(j)},相应地定义为基准矩阵X0(j)。基准矩阵和比较矩阵的数学关系如式(1)所示。
(1)
根据灰色系统理论,灰色关联系数
γi[x0(j),xi(j)]=
(2)
Δi(j)=|x0(j)-xi(j)| ;
(3)
mini=1,nminj=1,mΔi(j)=maxi(maxj|x0(j)-xi(j)|) ;
(4)
maxi=1,nmaxj=1,mΔi(j)=mini(minj|x0(j)-xi(j)|) 。
(5)
式中ρ为分辨系数,其作用是用来削弱二级最大差过大而失真的影响,以提高关联系数之间差异的显著性。
各比较序列及参考序列的关联度
(6)
值得注意的是,λ值作为评价指标来评估子序列和母序列之间的相关性。具体来说,λ值越接近于1.0,表明其所对应的参数的敏感性越强,变量之间的相关性越显著; 此外,λ值大于0.5即表明具有参数相关性。基于所建立的试验数据库,各变化参数对钢壳沉管自密实混凝土拌合物泵后性能的关联度计算结果如表2所示。可以看出: 泵送距离、弯头数量、输送时间和环境温度均与钢壳沉管自密实混凝土拌合物的泵后性能(入模温度、扩展度、V漏斗流动时间、L型仪H2/H1、含气量)存在关联性,且敏感性大小为环境温度>输送时间>弯头数量>泵送距离。

表2 灰色关联度计算结果
3 泵后性能预测模型的开发
3.1 支持向量机隐式模型
3.1.1 方法简介
支持向量机(Support vector machine,以下简称SVM)能够识别和表示复杂系统中的非线性关系,在回归和分类问题上具有很强的优势[19-20]。
SVM模型基于结构风险最小化理论,使训练数据集的误差(经验风险)最小化,同时使预测模型的泛化能力最大化,因此该方法具有强大的预测能力,可以很好地处理各种数据集。在SVM的非线性回归模型中,通过非线性映射(即核函数),低维空间被转化为高维空间,最终用高维空间中的线性方法解决非线性回归问题。在解决有限样本、非线性函数拟合等问题上,SVM模型优于其他多数机器学习算法。
3.1.2 SVM非线性回归预测模型
对于1组给定的训练数据{(x1,y1), (x2,y2),…, (xn,yn),x∈Rn,y∈Rn},SVM非线性回归预测模型可表示为
(7)
式中:τi(x)表示1组非线性变换;wi为权重;c为常数项。
引入不敏感损失函数ε并将其定义为
|y-f(x)|ε=

(8)

yi-f(x)≤ξi+ε(i=1, 2, …,n);
ξi>0 (i=1, 2, …,n) ;
ξi*>0 (i=1, 2, …,n) 。
(9)
采用拉格朗日乘子对模型进行优化,以解决非线性不等式约束的最优问题:
(10)
式中:L(w,c,ξ)为拉格朗日函数;χi、χi*、αi、αi*为大于0的拉格朗日乘子。
基于Wolf对偶理论,通过式(10)中w、c、ξ各自的偏导并令其值等于0,式(9)的对偶问题便可表示为
(11)
求解式(11),得到最优的αi和αi*,则得到最优的SVM非线性拟合函数
(12)
式中:K(xi,x)为用于调整和执行SVM非线性回归分析的核函数,主要包括线性、多项式、径向基和感知器型。
钢壳沉管自密实混凝土拌合物泵后性能与其变化参数之间的关系是不确定的,而SVM具有良好的非线性映射能力和鲁棒性,考虑将式(12)用于其泵后性能的预测是合适的。根据灰色关联理论的评估结果,本文采用泵送距离、弯头数量、输送时间和环境温度这4个重要参数作为SVM的输入变量。同时,将数据库按照3∶1的比例分为训练集和测试集,训练集用于训练SVM非线性回归模型,测试集用于验证机器学习预测结果的准确性。
3.2 贝叶斯显式模型
3.2.1 概率模型
由于自密实混凝土材料组成的特点,其泵送过程的敏感性较普通混凝土更显著。钢壳沉管自密实混凝土拌合物的泵后性能(入模温度、扩展度、V漏斗流动时间、L型仪H2/H1、含气量)受到不同因素的影响具有显著的随机性。因此,确定性预测模型在不确定性条件下难以充分考虑原材料性能、环境温度、施工时间、泵送施工工艺等影响因素的变化。相比于最小二乘回归模型,贝叶斯概率预测模型能合理地描述各关键参数的概率分布特性及由这些参数所引起的不确定性。贝叶斯推断通过对参数进行估计进而更新先验信息、提供预测的不确定性信息,采用该方法可为目标性能评估提供一类精确的概率预测动态模型[21-23]。基于上述讨论,建立了综合考虑泵送距离、弯头数量、输送时间和环境温度影响的自密实混凝土拌合物泵后性能的贝叶斯概率预测模型
Y=θX+b+σ2η。
(13)
式中:Y表示自密实混凝土拌合物泵后性能的概率预测值;θ=[θ1,θ2,θ3,θ4]T表示概率模型参数,综合反映了影响因素X=[x1,x2,x3,x4]T(泵送距离、弯头数量、输送时间和环境温度)存在的客观不确定性的影响;b为偏置项,综合反映了客观不确定性和主观确定性的影响;η为随机变量;σ2为后验分布所产生误差的方差。需特别说明的是,为使该概率模型适合测试结果,方差σ2应与因素X相互独立且不存在线性关系,且η服从标准正态分布。
由贝叶斯推断可以得到,参数(θ,σ)的无信息先验分布f(θ,σ)在(θ,σ)取值范围内是均匀分布的,其数学表达式为:
f(θ)∝1 。
(14)
(15)
其中参数θ的后验分布
(16)
式中:f(y|θ)表示似然函数;f(θ)表示先验分布。
3.2.2 计算结果
根据所建立的试验数据库,本文采用马尔科夫链-蒙特卡洛(MCMC)[24]对式(13)进行模拟抽样,最终确定参数(|θ,σ2|)的后验概率分布。自密实混凝土拌合物泵后性能的概率模型参数(θ,σ2)的运行结果如表3所示,由此得到基于贝叶斯-MCMC的概率预测模型如式(17)所示。
(17)
式中:y1、y2、y3、y4、y5分别为泵后自密实混凝土拌合物的入模温度、扩展度、V漏斗流动时间、L型仪H2/H1、含气量;x1、x2、x3、x4分别为泵送距离、弯头数量、输送时间、环境温度。
迭代形成马尔科夫链的入模温度模型参数的模拟轨迹如图2所示,其中迭代次数为10 000次。由图2可知,在随机模拟过程中,用于获取贝叶斯模型参数(θ,σ2)后验估计的样本均来自于收敛的马尔可夫链,从而保证概率预测模型具有良好的准确性、可靠性、鲁棒性。

表3 概率模型参数运行结果
3.3 模型验证与讨论
SVM机器学习算法可以有效发掘变量之间隐含的复杂非线性关系,通过提取模型参数并编译程序,将经过训练的模型集成到MATLAB软件中,便可作为计算工具应用于工程设计,方便工程人员使用;贝叶斯推断能够在数据样本容量较小的情况下估计总体分布。在实际工程应用方面,贝叶斯显式概率模型相对于SVM隐式模型更便于现场计算,且其模型综合考虑了自密实混凝土材料和施工工艺中主观、客观不确定性的影响,故计算简单实用、精度良好。通过结合本文所提出的2类模型,旨在实现基于目标泵后性能的关键参数调整施工工艺,可为后续沉管管节的混凝土拌合物泵送及同类工程提供有效参考。
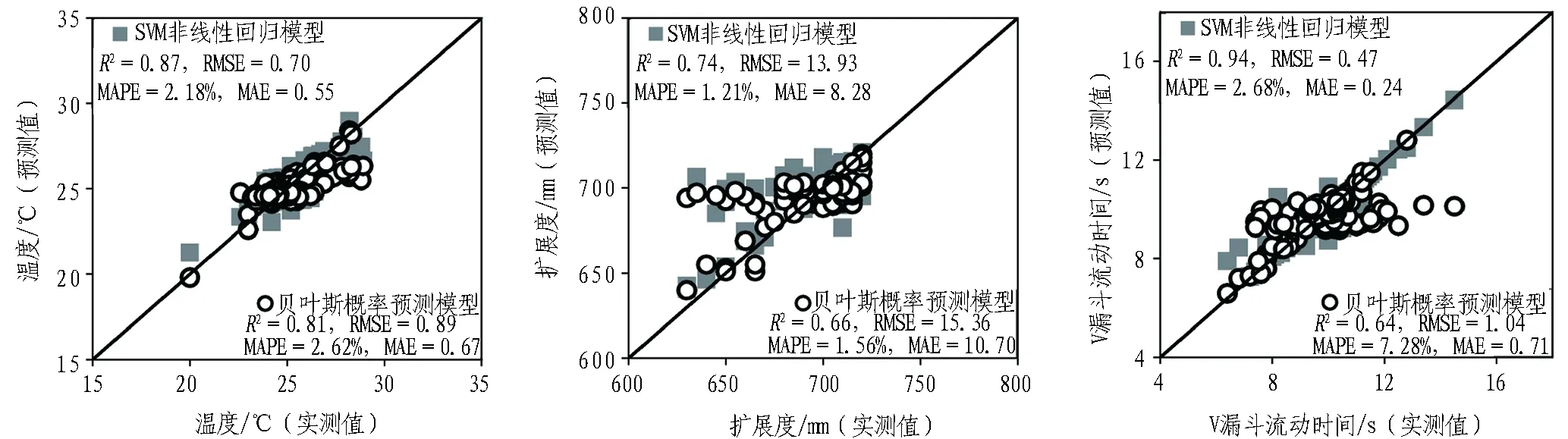
为了检验所开发的隐式和显式模型在预估钢壳沉管自密实混凝土拌合物泵后性能方面所具有的准确性,本文使用决定系数(R2)、均方根误差(RMSE)、平均绝对百分比误差(MAPE)和平均绝对误差(MAE)来对SVM回归模型和贝叶斯概率模型的精度进行综合比较分析。钢壳沉管自密实混凝土拌合物泵后性能的SVM回归模型预测值、贝叶斯概率模型预测值与实测值的比较如图3所示。以入模温度为例,在SVM回归模型中,R2=0.87,RMSE=0.70,MAPE=2.18%,MAE=0.55;在贝叶斯概率模型中,R2=0.81,RMSE=0.89,MAPE=2.62%,MAE=0.67。显然,所开发的2类模型的计算值都非常接近实测值,且偏差和随机性都较小,充分体现了机器学习和贝叶斯统计推断在钢壳沉管自密实混凝土拌合物泵后性能建模中的合理性与科学性,保证了预测结果的准确性与稳定性。
由图3可知,相比于贝叶斯线性概率模型,基于机器学习的SVM非线性预测模型具有全局最优性和较好的泛化能力,对于解决非线性计算问题具有显著的优越性,所得预测结果的准确性更高,但其局限性在于变量之间的数学关系为隐式表达,不便于施工现场快速设计计算; 而贝叶斯线性概率模型是一种显式动态模型,通过现场测试数据的实时反馈可丰富先验信息,便可对该模型进行基于贝叶斯理论的更新修正,由此得到具有更高的预测精度的后验模型。

(a) b的模拟轨迹图 (b) θ1的模拟轨迹图

(c) θ2的模拟轨迹图 (d) θ3的模拟轨迹图

(e) θ4的模拟轨迹图 (f) σ2的模拟轨迹图
为了验证本文提出的支持向量机隐式和贝叶斯显式预测模型具有普适性,另收集了使用另一种减水剂(醚类聚羧酸高性能减水剂,增加了消泡组分和30~60 min输送时间下的保坍组分)的50组额外试验数据进行扩展验证,所得模型的预测结果与实测结果的对比如图4所示。可以看出: 2类模型均具有较好的准确度和精度优势,进一步表明这2类计算方法均可为深中通道泵送自密实混凝土施工过程质量控制提供高效可靠的工作性能预估,对实际工程应用具有一定的参考价值。
(a) 温度 (b) 扩展度 (c) V漏斗流动时间
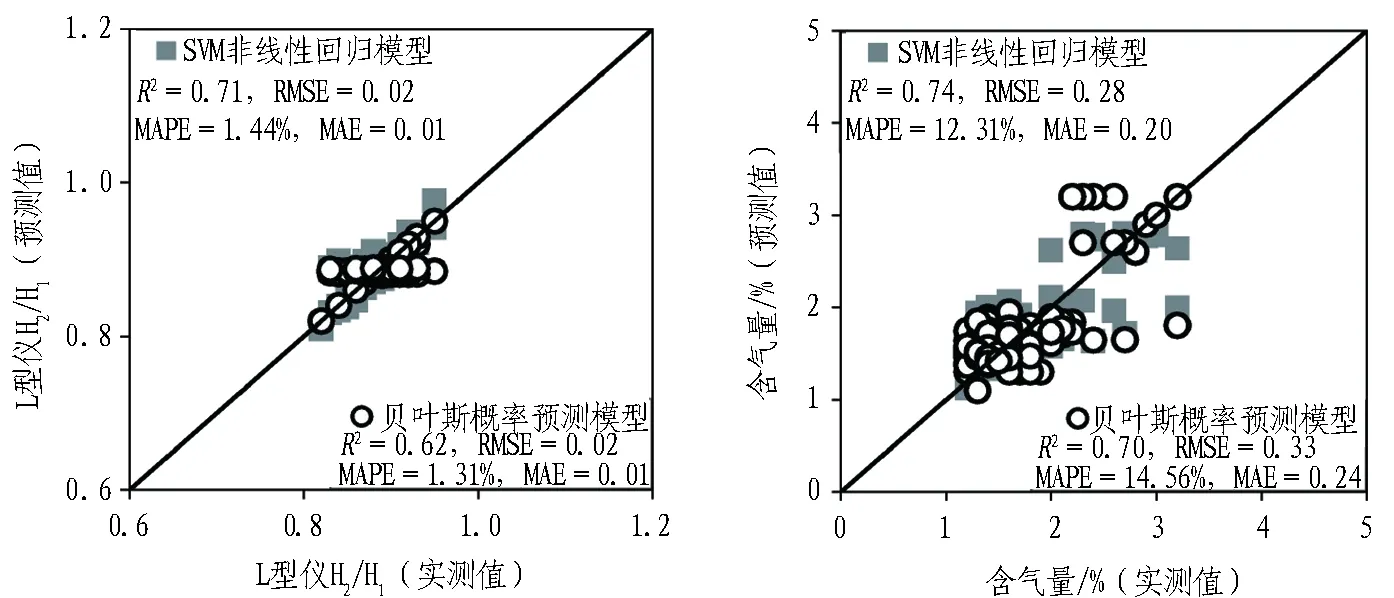
(d) L型仪H2/H1 (e) 含气量

(a) 温度 (b) 扩展度 (c) V漏斗流动时间

(d) L型仪H2/H1 (e) 含气量
4 结论与讨论
1)在整合现场实测数据信息的基础上,采用灰色关联分析对各类变化参数的敏感性进行了评价,结果表明: 泵送距离、弯头数量、输送时间和环境温度均与钢壳沉管自密实混凝土拌合物的泵后性能(入模温度、扩展度、V漏斗流动时间、L型仪H2/H1及含气量)存在关联性,且敏感性大小为环境温度>输送时间>弯头数量>泵送距离。
2)利用SVM机器学习和贝叶斯统计推断2类算法强大的数据挖掘能力,在不确定自变量与因变量精确数学关系的前提条件下,分别建立了钢壳沉管自密实混凝土拌合物泵后性能的隐式和显式预测模型,均在预测精度和预测稳定性方面收到了良好的效果。在预测精度方面,SVM 非线性模型比贝叶斯线性概率模型具有更大的优势,其依赖于算法的先进性,即基于结构风险最小化和线性二次规划理论发展起来的; 在实用性方面,贝叶斯显式概率模型相对于SVM隐式模型更便于现场计算,且其模型综合考虑了自密实混凝土材料和施工工艺中主观、客观不确定性的影响,该方法的适用性、可操作性更强。
3)所提出的SVM机器学习和贝叶斯线性概率模型分别是在进行了实测样本数据反复训练和10 000次迭代分析而产生的结果,故模型精度和可靠度较高,可为自密实混凝土拌合物泵后性能的预测提供新思路、新方法。然而上述2类模型缺乏明确的力学概念,同时本文没有提出成体系的自密实混凝土拌合物泵后性能计算程序,后续研究将建立具有一定力学概念的模型,同时开发出成体系的计算程序,从而更好地服务实际工程应用。
4)自密实混凝土拌合物泵后性能的预测是保证钢壳沉管浇筑质量的关键,后续工作将结合泵送自密实混凝土性能与自密实混凝土流变性之间的关系,进一步研究自密实混凝土在多种因素耦合下的性能损失机制。
