平转连续梁转体系统应力理论计算与数值模拟研究❋

田婷婷， 潘新颖❋❋， 郝小丽， 邓宏彦

(1. 中国海洋大学工程学院， 山东 青岛 266100； 2. 中交天津港湾工程设计院有限公司, 天津 300461)

目前，转体桥的应用非常普遍，可以在不影响铁路等交通运输正常运行的情况下，或者是在山谷、河流等不易施工的地方建设桥梁。主要是运用球铰系统的转体功能，在影响较小或方便施工的方向分段建立桥梁，再进行转体连接，形成连续的桥梁。此方法不仅质量可靠、施工安全，并且在车辆频繁的跨线桥或者通航河道的施工，可以不干扰交通、不间断通航，具有良好的适用性，而且还可以减少施工费用和机具设备使用，因此也具有良好的经济效益和社会效益[1]。转体方法大体可以分为三种：平转[2-5]、竖转[6]、平转竖转相结合[7-8]，其中应用较多的方法是平转法。由于转体吨位的不断增加，转体桥的建设也面临巨大挑战[9]。所以，应加强桥梁转体系统研究。目前，大多数转体系统的模拟研究，采用球铰应力理论值与SHELL单元模拟球铰的应力值进行对比研究或采用球铰应力理论值与SOLID单元模拟球铰的应力值进行对比研究。因此，本文对整个球铰系统应力的理论值， SHELL单元和SOLID单元模拟球铰的应力值进行综合对比研究。

1 转体系统理论计算

1.1 球铰理论计算

1.1.1 接触理论计算 根据弹性力学的接触理论，得到两球体之间接触的最大接触应力公式[10]：

(1)

式中：F为上部结构自重；E为球铰材料弹性模量；R1为上球铰的球面半径；R2为下球铰的球面半径。

因考虑球铰实际的接触状态，所以将下球铰的半径值取为负值进行计算。

1.1.2 等效应力计算 利用弹性力学中，半空间体在表面受法向分布力的理论[11]，结合材料力学中的第四强度理论[12]，对球铰之间的接触应力进行简化计算的方法。

将两球铰接触边界局部放大，考虑最大接触应力接触部分的特征与受力状态[13]。可以将球铰接触状态，近似为半空间体受均布力作用的模型，如图1所示。

图1 半空间体受均布力Fig.1 Uniform load on half space body

按照半空间体受均布力模型进行公式推导[11]：

(2)

(3)

(4)

式中：σx为x方向应力分量；σy为y方向应力分量；σz为z方向应力分量；q为均布法向荷载；μ为泊松比；a为均布荷载所作用圆面的半径。

当σz取极值-q时，根据复杂应力状态最大切应力公式[12]，计算τxz、τyz的最大值为0.1q。

根据Von Miss等效应力计算公式[14]：

(5)

计算得到球铰等效应力的最大值，并与数值模拟中等效应力计算结果进行对比验证。

1.2 下转盘理论计算

下转盘皆采用C50的混凝土，其抗压强度设计值fc为23.1 MPa。混凝土的计算压应力为[15]：

(6)

式中：K为偏压效应增大系数，取1.4；R′为下转盘与球铰接触面半径。

利用上式可以得到下转盘混凝土的计算压应力，小于C50混凝土的抗压强度设计值fc。

2 转体系统数值模拟计算

ANSYS大型有限元模拟软件，可模拟线性和非线性结构的应力状态，因此采用ANSYS有限元软件模拟球铰在恒定静力作用下，转体系统各部分的应力状态。此转体系统包括上、下转盘，球铰上、下铰盘。 此模型仅考虑转体系统在恒定静力作用下，球铰系统的应力变化规律。

2.1 单元类型及网格划分

在模拟过程中，上、下转盘部分的混凝土均采用SOLID65单元进行模拟。因SOLID65单元可以模拟无筋或有筋的3D混凝土实体[16]。其上、下球铰则采用了两种不同的单元进行对比模拟：一是采用SHELL181单元；二是采用SOLID185单元进行模拟。其中SHELL181单元为4节点的壳单元，可模拟薄壳以及中等厚度壳结构。SOLID185为8节点实体单元，可模拟多数实体结构[16]。

球铰结构间的接触由接触单元TARGE170和接触单元CONTA174组成。其中CONTA174为3D8节点面面接触单元，可与目标单元TARGE170模拟面面之间的接触和滑移状态[16]。具体单元类型如表1所示。

表1 单元类型Table 1 Element types

有限元模型网格的划分，因其主要研究对象为上、下球铰，所以对球铰部分的网格进行适当加密，以确保其结果的准确性，如图2所示。其中球铰采用SOLID185单元的模型共划分网格单元170 496个，球铰采用SHELL181单元的模型共划分网格单元167 164个。

图2 有限元模型网格划分Fig.2 Finite element model mesh division

2.2 接触模拟

上、下球铰之间的接触状态是通过定义下球铰为目标面，建立接触单元TARGE170，上球铰为接触面，建立接触单元CONTA174，两者共用实常数形成接触对进行模拟的[17]。球铰与混凝土之间的连接，可用两种方式模拟：一种采用整体模拟将球铰与混凝土进行固结；另一种是在球铰与混凝土之间建立接触对进行模拟。接触对模拟方式，其接触状态可通过约束方程、节点耦合或者MPC接触的方法进行模拟。本文需将SHELL单元与SOLID单元连接，所以接触建模方式采用MPC接触方法。MPC接触方法可以将需要连接的两部分，通过建立接触对，设置接触算法为MPC algorithm，实现不同单元间的连接[18]。球铰模拟采用SHELL181单元时，其球铰与混凝土间的连接涉及节点数量不同的单元连接问题，需设置参数较复杂，所以应根据工程实际选择接触参数。

根据不同单元类型和不同连接方式，本文数值模拟总体分为三种：(1)球铰采用SHELL181单元，且球铰与转盘之间采用MPC接触的方式连接；(2)球铰采用SOLID185单元，且球铰与转盘之间采用MPC接触的方式连接；(3)球铰采用SOLID185单元，且球铰与转盘之间采用整体模拟的方式连接。为研究不同单元模拟结果的精确性，特以求解条件大变形为对照，设置一个对照模拟组。

2.3 加载及求解

对模型的上转盘顶面施加竖向的均布荷载，对下转盘的混凝土底面施加约束，对整个模型采用静态分析进行求解。以模拟转体系统在恒定静力作用下的受力与约束状态。

3 工程算例

工程位于日照肖家庄地区，其承受重量最大的转体系统位于18、19号墩承台之上，如图3所示。转体系统所承受的荷载为12 500 t。转体系统各部分尺寸：上转盘直径长10.8 m，高3.115 m；球铰球面半径8 m，其中上铰盘球面半径8.02 m，下铰盘球面半径8.06 m；球铰平面半径2 m；铰盘厚度40 mm，如图3所示。

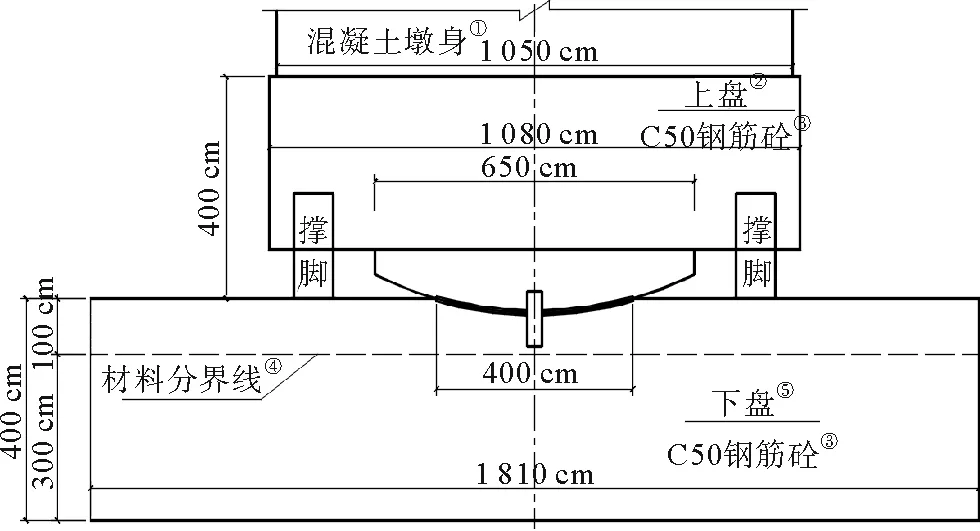
(①Concrete pier;②Upper rotating turnplate;③C50 reinforced concrete;④Material boundary;⑤Lower rotating turnplate)图3 转体结构立面图Fig.3 Elevation of swivel structure

上转盘采用的混凝土强度为C50，下转盘采用的混凝土强度为C50，其弹性模量取3.55×104MPa，泊松比为0.2。球铰为Q345钢板，其弹性模量取2.1×105MPa，泊松比为0.3，两球铰之间摩擦系数取0.1。

4 计算结果分析

4.1 理论计算结果

4.1.1 接触理论计算结果 根据理论计算方法，得到基于此工程的各理论方法的球铰应力计算结果，如表2所示。从中可以看出，等效应力计算值比接触理论计算值略大，其值更符合球铰的受力状态。

表2 球铰应力理论值对比Table 2 Comparison of theoretical values of stress on the ball joint

4.1.2 下转盘理论计算结果 基于上述公式，得到下转盘的混凝土压应力理论值为13.65 MPa，小于C50混凝土的抗压强度设计值，符合要求。

4.2 有限元计算结果

由有限元计算软件ANSYS计算出转体系统的各部分应力云图，并对球铰部分的等效应力云图以及下转盘混凝土部分的压应力值进行分析对比。

4.2.1 球铰应力结果 以小变形条件模拟为方案1，大变形条件模拟为方案2，两种方案的下球铰等效应力计算结果，如图4、5所示。

从图4、5中，可以看出小变形条件和大变形条件的下球铰等效应力分布规律基本一致，下球铰的大部分区域内等效应力值较小，球铰边缘附近的区域内等效应力值变化较大。图4(a)、5(a)中最大等效应力值分别为52.92和52.93 MPa，等效应力值大部分位于2.39～22.63 MPa。图4(b)、5(b)中最大等效应力值分别为52.82和52.83 MPa，等效应力值大部分位于2.38～22.56 MPa。图4(c)、5(c)中最大等效应力值分别为48.37和47.31 MPa，等效应力值大部分位于6.42～28.8 MPa。

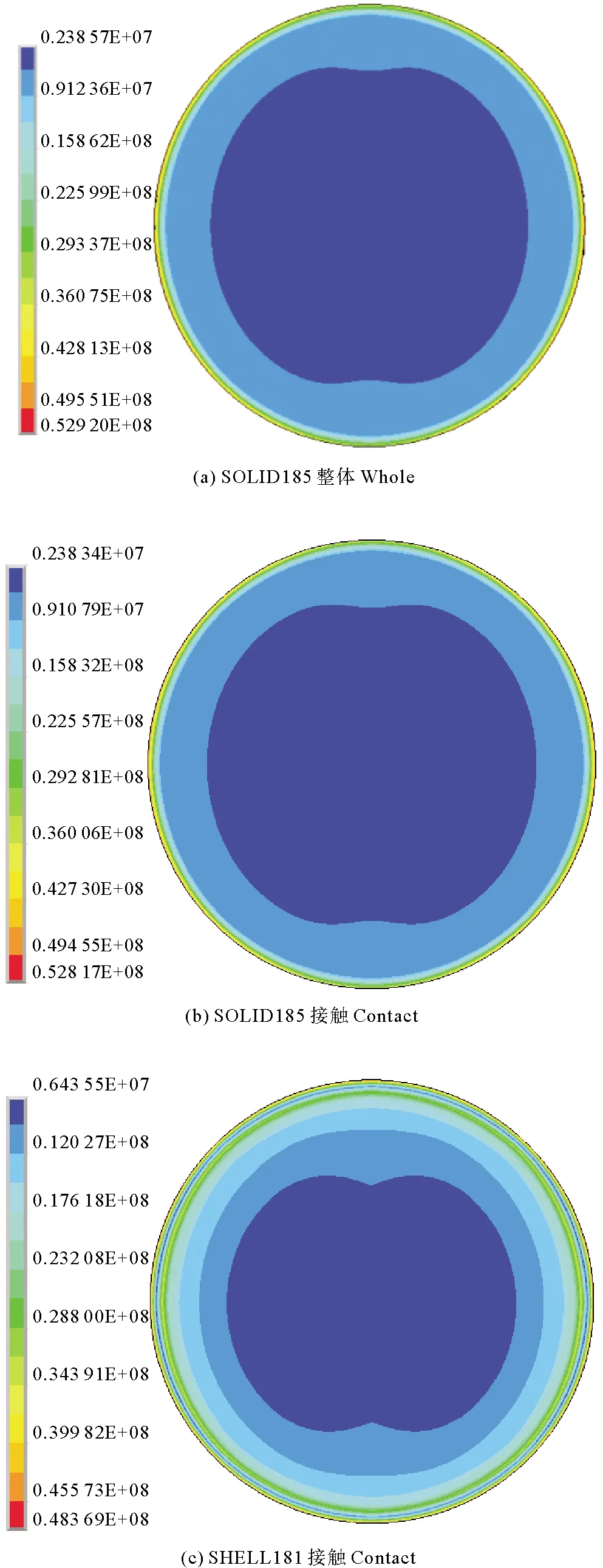
图4 下球铰等效应力(方案1)Fig.4 Equivalent stress of lower ball joint(scheme 1)

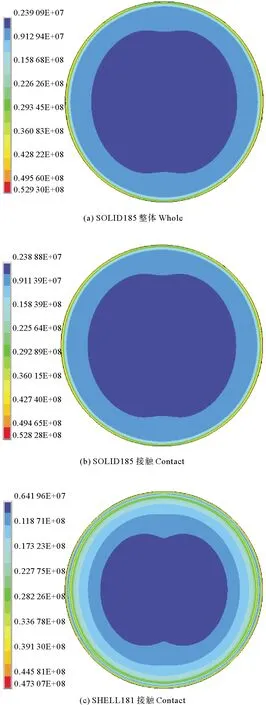
图5 下球铰等效应力(方案2)Fig.5 Equivalent stress of lower ball joint(scheme 2)

为进一步分析球铰等效应力值的变化情况，取球铰中心点到球铰边缘水平方向直线上的21个点，并提取对应点的等效应力值，以小变形条件下的3种模拟为一组，以大变形条件的模拟为对照组，绘制等效应力曲线对比图，如图6所示。

从图6中，可以看出三种模拟方式的下球铰等效应力变化趋势大致相同，且小变形和大变形之间结果差别较小，都是从球铰中心向球铰边缘处等效应力值不断增大。在球铰平面半径距离球心85%的范围内的等效应力值曲线变化都比较平缓，并且在此范围内SHELL的结果均大于SOLID结果，这是面单元与实体单元的结构差异造成的。球铰平面半径距离外边缘15%的范围内，6种方式的等效应力值都有较大的增加，是上转盘上方混凝土柱身的形状较球铰平面的形状更大造成的应力值突增。其中4种采用SOLID185单元的模拟，因为采用同种单元，仅连接方式和求解条件不同，所以其等效应力曲线基本吻合，而SHELL181单元的等效应力曲线较其他方式略有不同，因为SHELL181单元与SOLID185单元结构不同，所以在计算结果上有一定的偏差。

图6 下球铰等效应力曲线图Fig.6 Equivalent stress curve of lower ball joint

4.2.2 下转盘应力结果 从下转盘混凝土中心到距中心4 m处，x正方向的水平线上，平均取21个点，并提取对应点的压应力值，以小变形条件下的三种模拟为一组，以大变形条件的模拟为对照组，绘制下转盘混凝土压应力曲线对比图，如图7所示。

从图7中可以看出，下转盘混凝土的压应力分布云图的变化趋势与球铰的变化趋势基本一致，因为所提取的2 m内应力值为球铰与下转盘混凝土接触面上对应点的应力值，所以其2 m内的应力值变化趋势与球铰应力变化基本相同。2～4 m范围内因无外部荷载，所以其应力值有较大幅度的回升。

图7 下转盘压应力曲线图Fig.7 Compressive stress curve of lower rotating turnplate

4.3 结果对比

4.3.1 球铰结果对比

(1)有限元模拟结果对比

有限元模拟以三种不同方式进行模拟，并以大变形求解条件为对照方案2，对比结果如表3。

从表3中可以看出，方案1和方案2的结果相差很小，说明模拟球铰转体系统时，采用小变形求解即可。表3中，SHELL单元模拟的球铰应力值之差是SOLID单元差值的100倍左右，可见采用SOLID单元模拟球铰，等效应力结果更加稳定。其中SOLID整体的模拟方式，其等效应力值略微偏大，是模拟时对球铰与混凝土之间相互作用的简化造成的，所以采用MPC接触的方式，模拟球铰接触状态更符合实际。

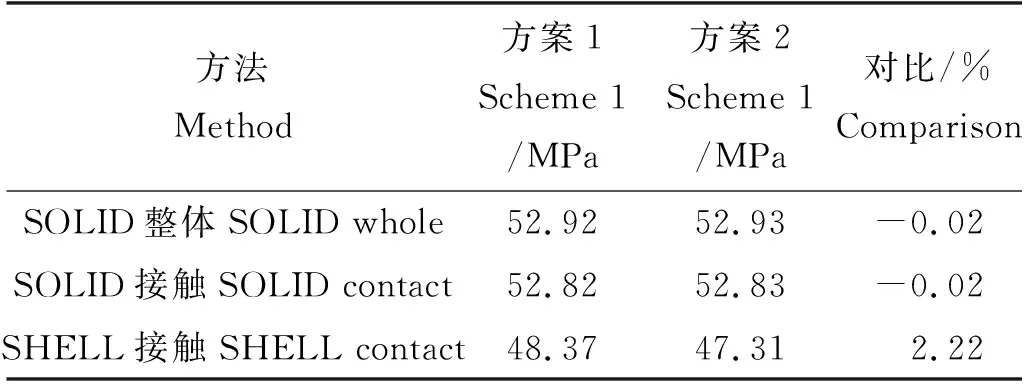
表3 球铰有限元模型等效应力最大值对比Table 3 Comparison of the maximum equivalent stress on the finite element model of ball joint

(2)有限元模拟结果与理论结果对比

以工程为例，利用弹性力学接触理论和等效应力计算的方法，计算上、下球铰在恒定静力作用下的球铰接触应力理论值，与有限元仿真模拟中SOLID接触结果进行对比，得到球铰应力值对比表，如表4所示。

表4 球铰应力值对比Table 4 Comparison of stress values on the ball joint

从表4中可以看出，等效应力计算的理论值与有限元仿真模拟的球铰等效应力值相比仅差3.01%，说明等效应力计算求解的球铰应力理论值较为准确。而弹性力学接触理论计算方法，仅考虑两球体受压接触时的接触应力与形变[13]，因而结果偏小。从理论计算结果中，可看出SHELL接触的结果较理论值小，与大多数研究中有限元模拟结果偏大不同，因此与之前结论一致SOLID模拟球铰更准确。

4.3.2 下转盘结果对比 下转盘理论计算结果为13.65 MPa。ANSYS模拟的三种情况以及对照组的结果，表明所有情况的下转盘混凝土压应力最大值，均小于C50混凝土的抗压强度设计值 ，皆符合要求。

5 结论

通过对球铰转体系统进行模拟，研究分析其模拟结果。可以得到以下结论：

(1)在恒载作用下，球铰应力的分布呈现从球铰中心向球铰边缘逐步增大的规律。

(2)球铰应力值，在球铰平面半径距离球心85%的范围内应力值较平缓；在球铰平面半径距离外边缘15%的范围内有较大的增加，此区域应为球铰设计重点关注区域。

(3)球铰理论计算中，采用等效应力计算方法，得到的球铰接触应力理论值较准确。

(4)ANSYS数值模拟计算球铰应力时，球铰采用SOLID单元计算结果更稳定、更准确，且求解时采用小变形条件即可。