西安200 MeV质子应用装置同步环线性光学测量与校正

杨 业， 王敏文， 叶文博， 刘晓宇， 李 岩，姚红娟， 郑曙昕， 刘卧龙， 王 迪， 王茂成， 赵铭彤，闫逸花， 张 辉， 王百川， 吕 伟， 王忠明†

(1. 强脉冲辐射环境模拟与效应国家重点实验室， 西安 710024；2. 粒子技术与辐射成像教育部重点实验室， 北京 100084；3. 清华大学 先进辐射源及应用实验室， 北京 100084； 4. 清华大学 工程物理系， 北京 100084)

西安200 MeV质子应用装置(Xi’an 200 MeV Proton Application Facility， XiPAF)是国内首台满足空间质子单粒子效应考核要求的实验装置，该装置由7 MeV直线注入器和200 MeV同步加速器组成[1-3]。调束阶段，由于存在准直偏差和磁铁磁场偏差，同步加速器的线性光学与设计会有偏差。为建立准确的机器模型及优化注入、加速和引出效率，线性光学测量与校正是环形加速器调束过程中关键且必要的一步。表征环形加速器状态的线性光学函数包括工作点、β函数、色散函数和色品。常用的线性光学校正方法有2种[4]：第1种是基于闭轨响应矩阵的校正方法，该方法主要用于轻子储存环的线性光学校正[5-7]，也可应用于中小型强子同步环的线性光学校正[8-9]，但受限于束流位置探测器(BPM)的测量噪声，模型校正效果有限；第2种是基于束流逐圈位置的校正方法，需要激励起较大幅度的束流质心振荡，在强子和轻子环形加速器中都有应用[10-12]。

当前，调束在临时厂房进行，BPM逐圈位置测量噪声比较大，基于束流逐圈位置的测量与校正方法的效果不太好，因此采用了基于闭轨响应矩阵的校正方法和LOCO(linear optics from closed orbits)程序[13-14]进行线性光学校正。本文首先介绍了工作点、β函数、色散函数和色品的测量方法与结果，然后改进了LOCO程序，使之适用于低能质子同步加速器的线性光学校正，最后给出了基于改进后LOCO程序的校正结果。

1 XiPAF同步环简介

XiPAF同步加速器是一个周长30.9 m、采用六折对称结构的紧凑型同步加速器[1-3]，该装置的布局如图1所示。

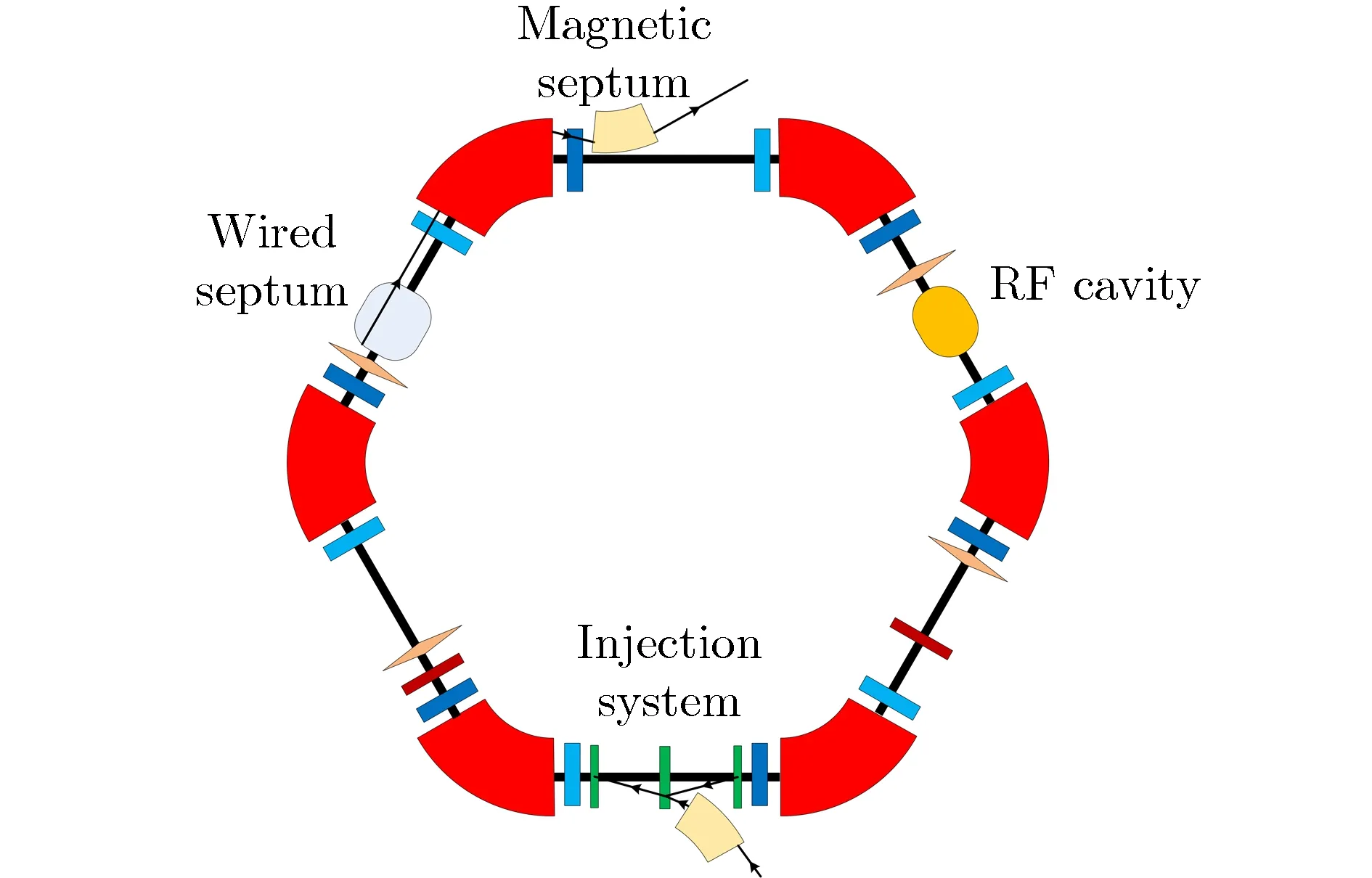
图1 XiPAF同步环布局Fig.1 Layout of XiPAF synchrotron

每个单元类似于1个将二极铁取消的FODO结构，因此称为“Missing dipole FODO”结构。该方案简单且有足够的直线节放置束流测量元件、高频腔及注入引出等相关设备。每个单元放置1个水平校正铁和1个垂直校正铁。每个校正铁附近放置1个同方向的BPM，因此环上总共有12个单向校正铁和12个单向BPM。通过这些校正铁和BPM可以实现响应矩阵测量以及闭轨校正。XiPAF采用H-剥离注入，为方便放置注入切割磁铁，通过3个直流凸轨磁铁产生局部凸轨[15]，使环光学参数失去了六折对称性。

由于注入和引出阶段所需的工作点不同，XiPAF同步环采用了变工作点的加速方式，注入和引出阶段的光学参数,如表1所列。注入引出阶段对光学模型的准确性都有很高的要求，因此都需要进行光学函数的测量与校正。2个阶段的光学函数测量与校正过程类似，本文只介绍注入阶段的光学函数测量与校正。

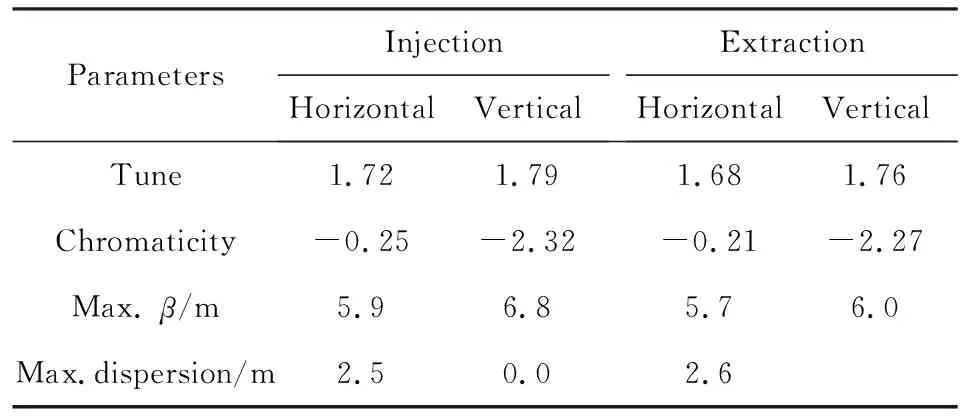
表1 同步环光学参数Tab.1 Lattice parameters of synchrotron ininjection and extraction phase

XiPAF同步环注入阶段的β函数如图2所示。由图2可见，受凸轨磁铁边缘场的影响，垂直方向βy函数失去了六折对称性。

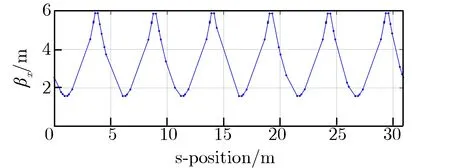
(a) βx

2 线性光学测量与校正方法

2.1 线性光学测量原理与方法

常用的线性光学函数包括工作点、β函数、色散函数和色品。工作点可采用对BPM逐圈位置做快速傅里叶变换(FFT)和频谱仪直接对BPM原始信号做谱分析2种方法进行测量。为提高工作点测量精度，在测量前使用白噪声激励束流，产生一定幅度的横向振荡。

β函数的测量方法有2种[4]。

第1种称为K调制法。当四极铁聚焦强度变化较小时，在线性近似下，工作点的变化为

(1)

其中， Δvx,y为水平或垂直工作点变化； Δk为四极铁聚焦强度变化；βx,y为四极铁处的平均β函数；L为四极铁有效长度。测量时通过漂浮电源逐个改变四极铁聚焦强度，测量工作点变化，通过线性拟合得到四极铁处的平均β函数。

第2种方法称为ORM(orbit response matrix)方法。当校正铁与BPM位置非常近时，可认为校正铁与BPM处的β函数和色散函数相等，相移为0，此时给校正铁施加踢角θ引起的BPM位置变化为

(2)

其中， Δux,y为施加校正铁踢角后水平或垂直束流位置变化；η为同步环滑相因子；Dx,y为校正铁或者BPM处的色散函数；C为同步环周长。由式(2)可知， Δux,y与θ呈线性关系，测量时逐个扫描校正铁磁场，测量束流位置变化，线性拟合后得到线性响应系数，代入式(2)即可得到校正铁与BPM处的平均β函数。

色散和色品都是由束流能量偏差而引入的参数，因此，要测量色散和色品需要引入束流能量的微小变化，通过缓慢改变高频腔的频率实现束流能量的微调。在频率变化很小时，频率变化可表示为[16]

(3)

其中，f为高频频率；p为与频率f匹配的束流动量； Δf频率变化量； Δp为束流动量变化量。实际测量时，给定频率线性缓慢变化的频率曲线，测量频率变化过程中的束流位置和工作点的变化。束流位置随束流动量偏差变化关系的线性系数即为色散函数，束流工作点随束流动量偏差变化关系的线性系数即为色品。

2.2 基于ORM的线性光学校正方法

由于响应矩阵中已经包含了关于横向运动的所有信息，将测量的响应矩阵与模型计算的响应矩阵进行匹配，即可修正模型，并得到一个与实际测量结果相匹配的Lattice模型，这就是基于ORM的线性光学校正的基本思想。LOCO程序是基于Matlab开发的，以加速器工具箱(Accelerator Toolbox，AT)为计算模型的ORM线性光学校正程序[13-14]，该程序已经广泛应用于环形加速器的线性光学校正[5-9]。

LOCO的基本原理就是以四极铁强度、BPM增益系数、校正铁强度及校正铁耦合等为匹配变量，调节这些变量，使模型和测量得到的响应矩阵相等。偏差函数可定义为

(4)

其中，Gmodel,i,j为模型计算得到响应矩阵的第i行第j列元素，i表示BPM，j表示校正铁；Gmeas,i,j为测量得到响应矩阵的第i行第j列元素；σi是第i个BPM的噪声水平。改变匹配变量的值，使得上述偏差函数最小，是一个多参数单目标的非线性优化问题。求解该问题最有效的方法是高斯牛顿法，通过求解每一步迭代时的雅克比矩阵，采用最小二乘法得到下一步匹配变量的修正量，使偏差函数逼近全局最小值。但该方法对初值敏感，当初值偏差较大时，会出现迭代发散或者振荡。为解决该问题，LOCO程序采用了Levenberg-Marquadt方法求解，结合了高斯牛顿法和最速下降法2种算法的优点，可通过惩罚因子来控制算法。当初值偏差较大时，采用较大的惩罚因子使算法更接近于最速下降法，该算法始终是收敛的，可使变量不断逼近全局最小值，随后采用较小的惩罚因子加快收敛速度。变量匹配过程中，四极铁强度的偏差对同步环的线性光学影响很大。利用Levenberg-Marquadt方法可得到四极铁强度拟合值Kps，及其与设计值K的偏差ΔK。四级铁工作电流的校正量ΔI与强度K的关系可表示为

(5)

Kps可认为是实际四极铁强度的最佳估计值，利用式(5)可得到四极铁工作电流的校正量，将新的工作电流发给四极铁电源即可将实际的加速器Lattice校正到与设计的加速器Lattice相匹配。

3 线性光学函数测量与校正结果

在同步环注入俘获后进行了线性光学函数与响应矩阵的测量，以中能输运线上的BPM为相位探针，通过飞行时间法(time of flight, TOF)测得注入束流能量为7.11 MeV。按2节介绍的方法测量了响应矩阵、β函数、色散函数和色品。由于开源的LOCO和AT程序最初是针对电子储存环设计，为了使2者可以应用于低能质子环的模拟与线性光学校正，需对程序做一定的修改。电子加速到较低能量时，速度接近光速，在跟踪时可直接将电子的速度默认为光速；与电子相比，低能质子的非相对论效应明显，在跟踪时需考虑速度的影响。程序修改的内容为

1) 在AT中对二极铁、四极铁及高频腔等元件增加新的跟踪算法，主要是在纵向坐标的跟踪中加入了粒子速度的影响。

2) 修改了LOCO程序中响应矩阵计算的理论公式，原有的程序中，式(2)中的η为动量压缩因子，这对于相对论粒子束是适用的，但对于非相对论粒子束，需考虑粒子速度的影响，必须使用滑相因子。

为了使初始模型尽可能准确，在初始模型中考虑了二极铁的四极分量、六极分量和八极分量的影响，元件初始参数均按照机器实际运行参数进行设置。LOCO校正的匹配变量包括四极铁聚焦强度、校正铁增益及BPM增益。同时将测量的色散函数作为响应矩阵的一部分进行拟合。由于垂直方向色散函数非常小，参与拟合会出现迭代不收敛的情况，所以将垂直方向色散的权重设置为0。频率测量较准确，拟合过程中不将频率作为拟合参数之一。

XiPAF同步环校正铁和BPM数量较少，响应矩阵中的有效数据也较少，使用LOCO进行横向耦合的校正时会出现结果不收敛的现象。这是因为机器实际的横向耦合比较小，但可能产生横向耦合的因素较多，如二极铁和四极铁的滚转角偏差。如果将二极铁和四极铁滚转角偏差作为拟合参数，拟合参数较多会导致结果不收敛。在不考虑横向耦合的情况下，迭代一次，结果基本就收敛了，后续拟合的偏差基本不变。在实际测量中，第1次迭代后，偏差由516减小到2.17。第1次迭代后，测量与模型响应矩阵的3维图如图3所示。模型和测量响应矩阵的最大相对偏差为7%，符合较好。

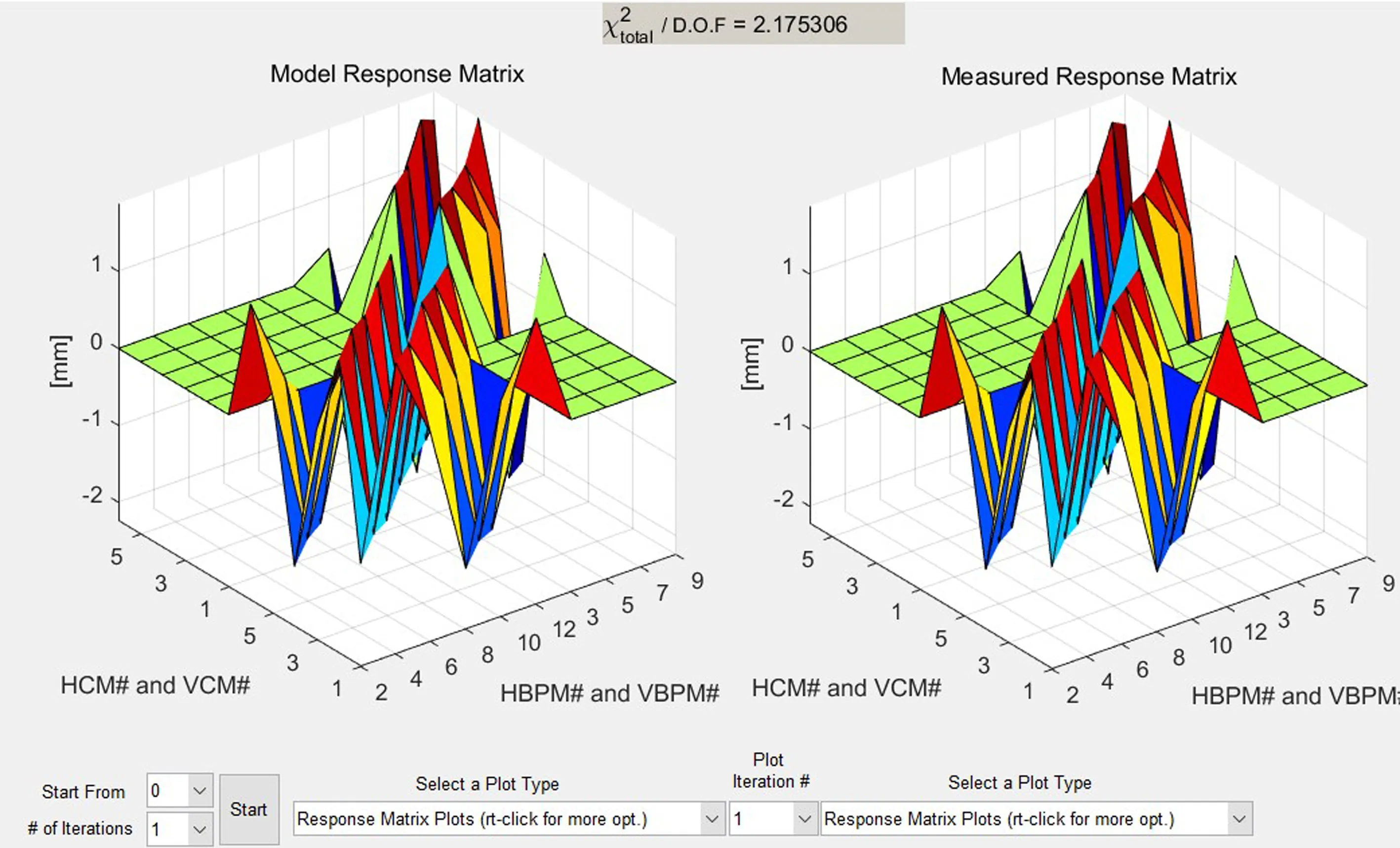
图3 校正后模型响应矩阵与测量响应矩阵对比Fig.3 Corrected response matrix vs. measured response matrix

XiPAF同步环有3类四极铁，分别由3个电源供电，在拟合过程中将同1类四极铁的聚焦强度作为1个参数处理，因此四极铁聚焦强度有3个匹配变量。通过修正后的四极铁聚焦强度与根据电流和测磁曲线计算得到的聚焦强度，可确定四极铁修正系数(fudge factor)，如表2所列。

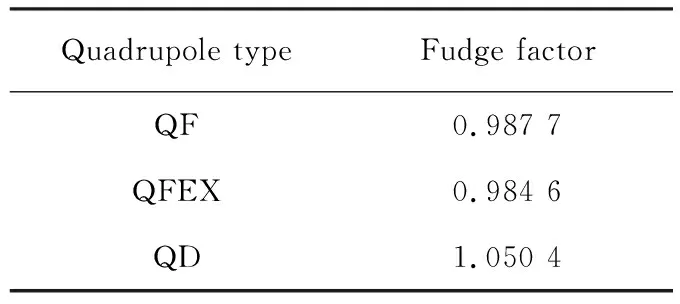
表2 四极铁修正系数Tab.2 Fudge factors for quadrupole type

为验证校正后模型的准确性，将测量的β函数、色散函数及色品与校正模型给出的结果做了对比。图4为校正后模型β函数与测量β函数的对比，其中，“modelβ”为校正模型计算得到β函数，“quadβ”为K调制法测量得到的β函数、“corrβ”为ORM方法测量得到的β函数。由图4可见，由于7 MeV注入俘获后垂直方向动量分散较大，且垂直方向色品较大，使工作点无法准确测量，因此垂直方向没有使用K调制法测量β函数。

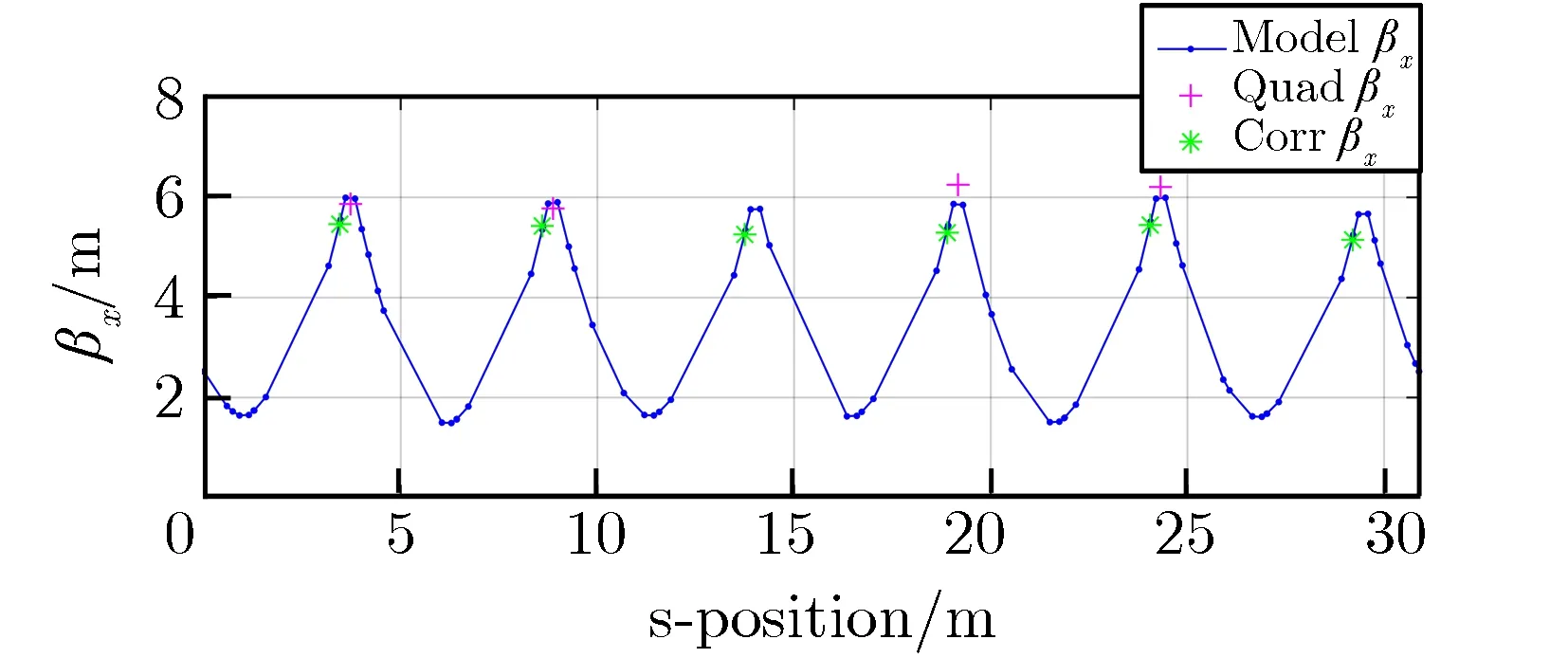
(a) βx

图5为校正后模型色散函数与测量色散函数的对比。其中，“modelD”表示校正模型计算得到色散函数，“measureDoriginal”表示测量得到的原始色散函数，“measureD”表示用LOCO校正得到的BPM增益系数对测量得到的色散函数进行修正后的结果。由图5可见，修正后的色散函数与模型符合的非常好，表明LOCO校正给出的BPM增益系数是比较准的。由于LOCO校正没有拟合耦合项，所以垂直方向模型给出的色散函数为0。

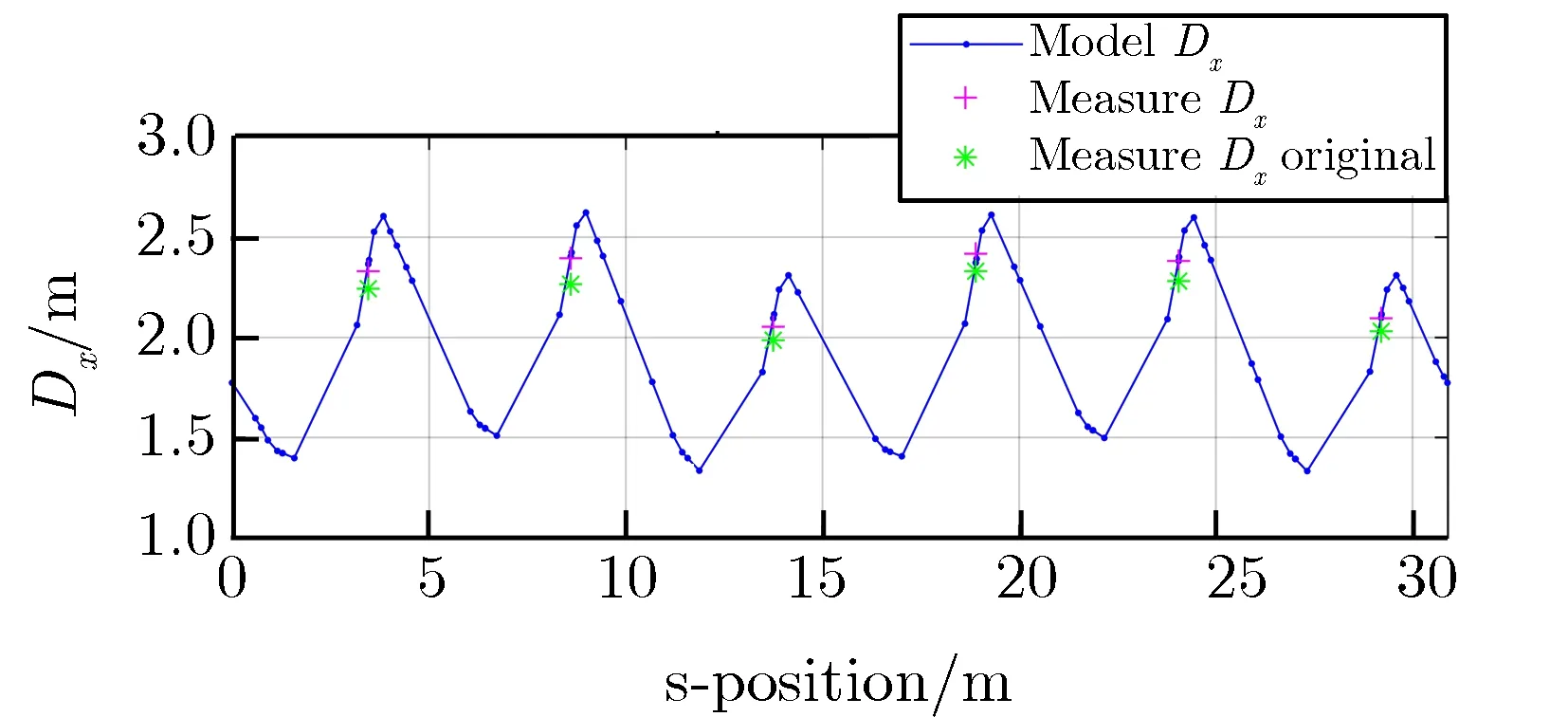
(a) Dx

测量得到的水平方向的色品ξx,meas=0.33，垂直方向的色品ξy,meas=-2.83。考虑不同二极铁高阶场分量时，使用MADX计算了校正模型的色品，如表3所列。由表3可知，影响色品的主要是六极分量，与理论相符。测量的色品与考虑二极铁六极分量之后校正模型的色品非常接近，说明测量色品和自然色品的差异主要是由二极铁六极分量引起的。

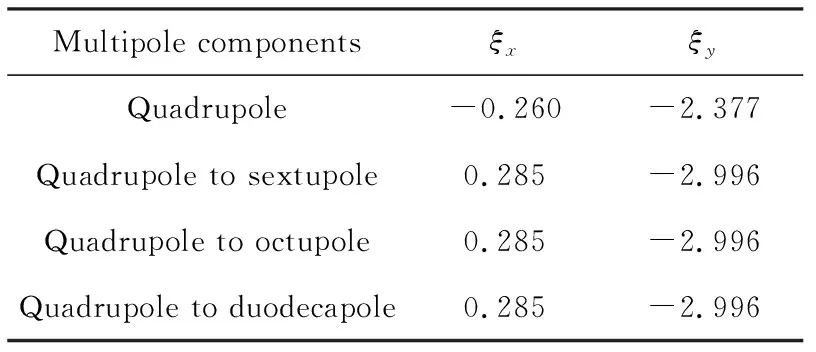
表3 考虑不同高阶场分量时校正模型的色品Tab.3 Chromaticity of correction model consideringdifferent multipole components

4 结论

本文介绍了XiPAF同步环线性光学测量与校正的结果，校正后的模型与测量的线性光学函数符合较好，说明在对相关模型做修正后，LOCO程序可应用于低能质子同步加速器的线性光学校正。由于小型质子同步加速器结构紧凑，BPM和校正铁数量较少，导致有效的数据不多，且低能质子装置BPM噪声较大，因此无法精确地拟合一些精细的模型参数；但可拟合影响线性光学的主要参数，如四极铁强度，迭代一次即可收敛，拟合精度基本满足机器建模和线性光学应用需求。