非高斯环境下船变测量最大熵卡尔曼滤波方法

龙子旋, 周 琪, 彭侠夫, 张霄力,*

(1.厦门大学航空航天学院, 福建 厦门 361101;2.中国航空工业集团公司西安飞行自动控制研究所, 陕西 西安 710076)

0 引 言

惯性量匹配方法因其精度高、实时性好而在船体变形测量中得到广泛应用,其本质就是建立船变测量过程的卡尔曼滤波方程。目前主流的惯性匹配算法包括角速度匹配法[1-3]、姿态阵匹配法[4-5]、姿态角匹配法[6]和姿态四元数匹配法[7-8]。

文献[9]指出,当噪声建模失准或测量系统受到未知噪声干扰时,传统卡尔曼滤波或无法准确跟踪角形变。在船体变形测量中,为简化建模过程,往往将量测噪声理想化为模型准确已知的高斯白噪声,对模型失准系统受到有色噪声干扰下的滤波研究较少。文献[10]将系统噪声建模为白噪声驱动的有色噪声,然后修改了卡尔曼滤波器的迭代方程来完成非高斯滤波。文献[11]提出了一种强跟踪的最大互相关熵(简称为最大熵)卡尔曼滤波,即将自适应因子引入传统的最大熵滤波器改进姿态阵匹配法,减小模型失配误差。

针对噪声统计特性建模失准问题,学者们提出了一种自适应卡尔曼滤波,其核心思想是,利用量测数据自动进行相关迭代矩阵的在线估计和修正。文献[12-13]介绍了一种Sage-Husa自适应卡尔曼滤波,该滤波器引入单一的遗忘因子来减小历史数据的影响,直接估计噪声的一阶和二阶统计特性。此后,单自适应渐消因子的概念被提出,其本质是强迫新息协方差的理论值与估计值相等以稳定滤波过程[14]。文献[15-18]引入多通道自适应渐消因子对状态一步预测误差矩阵进行实时更新调整以实现对多通道时变噪声的自适应。此外,文献[19-20]还引入了χ2检验来提高自适应渐消因子引入时机,抑制可能出现的状态跳变,成功应用于捷联惯性导航系统(strapdown inertial navigation system, SINS)初始对准问题,并推广到非线性系统中[19]。

针对非高斯白噪声的滤波问题,在信息论(information theoretical learning, ITL)中,有关学者提出了另一种最优理论,即最大熵准则(maximum correntropy criterion, MCC)[21-22]。其核心思想是,在卡尔曼滤波迭代过程中引入MCC构造核函数,以此作为卡尔曼滤波器的目标函数,重新求解滤波器的增益矩阵,充分利用量测值的高阶信息,这便是用来处理非高斯噪声的最大相关熵卡尔曼滤波器。文献[23]在进行增益矩阵的求解时,近似认为状态值与一步预测值相等,得到基于MCC的卡尔曼滤波迭代(MCC Kalman filter, MCKF)算法,由于其近似处理较多,故而其算法简单但滤波器精度较差。文献[24]通过改进近似处理过程并融合加权最小二乘(weighted least squares, WLS)理论修改高斯核函数得到性能更优的非高斯滤波器,其滤波收敛性更好、精度更高、稳定性更好。此外,基于扩展卡尔曼滤波器(extend Kalman filter, EKF)和无迹卡尔曼滤波器(unscented Kalman filter, UKF)的最大熵滤波器也相继被提出以解决工程遇到的实际问题[25-26],将MCC推广到非线性系统,进一步说明了MCC在非线性环境中同样适用。

受相关论文启发,本文介绍一种基于权重矩阵的MCCKF算法解决船体变形角估计中遇到的实际工程问题。

首先，介绍了最大熵概念,推导了传统MCKF和改进MCCKF迭代公式。然后,引入两种主流自适应滤波器:多重自适应渐消因子滤波器(简称为MAKF)和基于χ2检验的多重自适应渐消因子滤波器(简称为TAKF),并与MCKF一同作为对比算法，基于船体变形角估计应用场景,在两种典型非高斯噪声和两种船体静态变形建模情形下,针对4种滤波器开展多组对比实验。此外,还探讨了MAKF、TAKF实际使用受限问题。最后，通过实验结果分析,验证了本文介绍的滤波算法在收敛性、变形估计精度、实用性等综合性能上相对于主流自适应和最大熵滤波器具备一定的优越性。

1 MCKF

1.1 传统MCKF

MCC准则可充分利用信息的高阶统计特性来衡量两个随机变量之间的相关性[27-28],在非高斯环境中的滤波有广泛的应用[29-30]。最大相关熵滤波器源于对经典卡尔曼滤波迭代公式中的代价函数(又称目标函数)进行替换继而推导得到的。首先,采用如下形式的高斯核函数替代目标函数:

(1)

式(1)表明新的高斯核函数由两个核函数组成,其中,

(2)

类似于标准卡尔曼滤波器的最小均方误差(minimum square error, MSE)理论求解最优解的方式,求解式(2)的最大熵,令

(3)

得

(4)

即

(5)

为求状态变量更新公式,通常在较短滤波更新周期内认为

(6)

则,式(5)中可有以下相关近似项:

(7)

式中:I为n维的单位矩阵。

联立式(5)与式(7)得到状态量更新公式:

(8)

式中：增益矩阵可表示为

(9)

(10)

(11)

(12)

最后求得改进后的MCKF状态量更新公式:

(13)

式(13)还可以得到状态预测的增益矩阵:

(14)

用式(13)和式(14)替换掉经典卡尔曼滤波状态更新公式便可得到MCKF的迭代算法。算法流程如下所示。

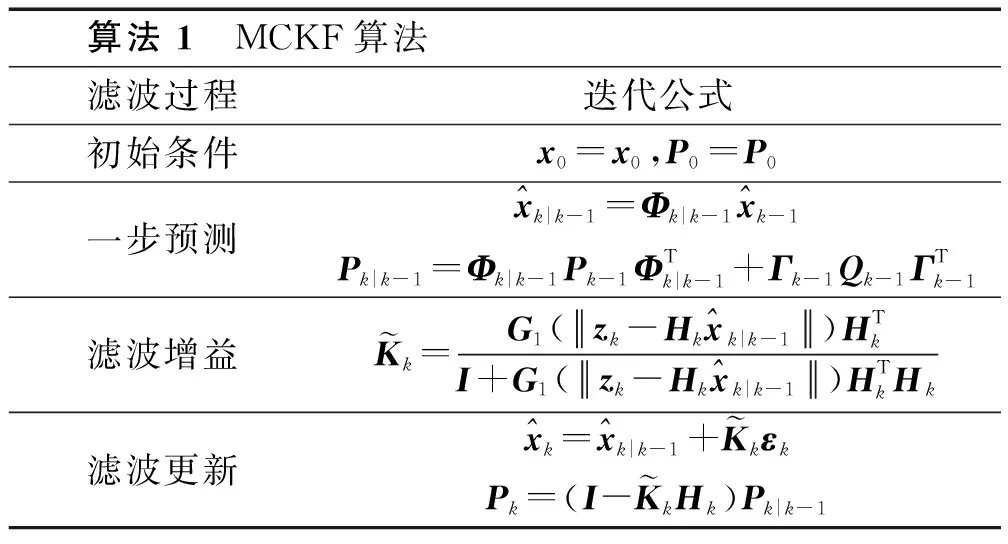
算法1 MCKF算法滤波过程迭代公式初始条件x0=x0,P0=P0一步预测^xk|k-1=Φk|k-1^xk-1Pk|k-1=Φk|k-1Pk-1ΦTk|k-1+Γk-1Qk-1ΓTk-1滤波增益 Kk=G1(zk-Hk^xk|k-1)HTkI+G1(zk-Hk^xk|k-1)HTkHk滤波更新^xk=^xk|k-1+ KkεkPk=(I- KkHk)Pk|k-1

1.2 改进型MCCKF

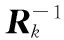
(15)

类似式(3)方式求其最优解,得

(16)

将式(16)改写为

(17)

其中,

(18)

类似式(11)的处理,得

(19)

最后求得MCCKF状态量更新公式:

(20)

类似式(14),得到滤波过程的增益矩阵为

(21)

同样, MCCKF迭代算法流程如下所示。

算法2 MCCKF算法滤波过程迭代公式初始条件x0=x0,P0=P0一步预测^xk|k-1=Φk|k-1^xk-1Pk|k-1=Φk|k-1Pk-1ΦTk|k-1+Γk-1Qk-1ΓTk-1滤波增益^Kk=GkHTkR-1kP-1k|k-1+GkHTkR-1kHk滤波更新^xk=^xk|k-1+^KkεkPk=(I-^KkHk)Pk|k-1

2 实验与分析

目前角速度匹配法在惯性匹配方式体系中应用较广、技术成熟,因此以下变形滤波验证实验亦基于此。另外,因试验无法提供基准及真实数据,以下验证实验均以计算机仿真平台为主。

2.1 角速度匹配法和实验参数设置

船体变形角包括静态变形角和动态变形角。静态变形视为“准静态”模型,用随机游走模型近似代替其长周期的缓变过程:

(22)

动态变形θi视为白噪声信号通过二阶滤波器得到,其模型如下:

(23)

式中：i=x,y,z。光纤陀螺器件漂移模型分为两类,即常值漂移εc和偏置稳定性漂移εr,前者视为常量,后者视作一阶Markov过程:

(24)

式中：j=1,2。式(23)和式(24)相关参数含义如表1所示。

表1 船体变形模型关键参数

综合以上变形模型、陀螺漂移模型,将角速度匹配方法的状态方程组表示如下:

(25)

另外,量测方程为

(26)

(27)

其中,各个矩阵的含义由于篇幅有限这里不作展开。实验给定的船变参数如表1所示。对摇摆谱的选择需要符合船舶航行的海浪实况,实测数据表明摇摆激励越小,观测量越小,变形结果耦合的地速就越大,精度越低。表1中船体静、动态变形角示意图如图1所示。

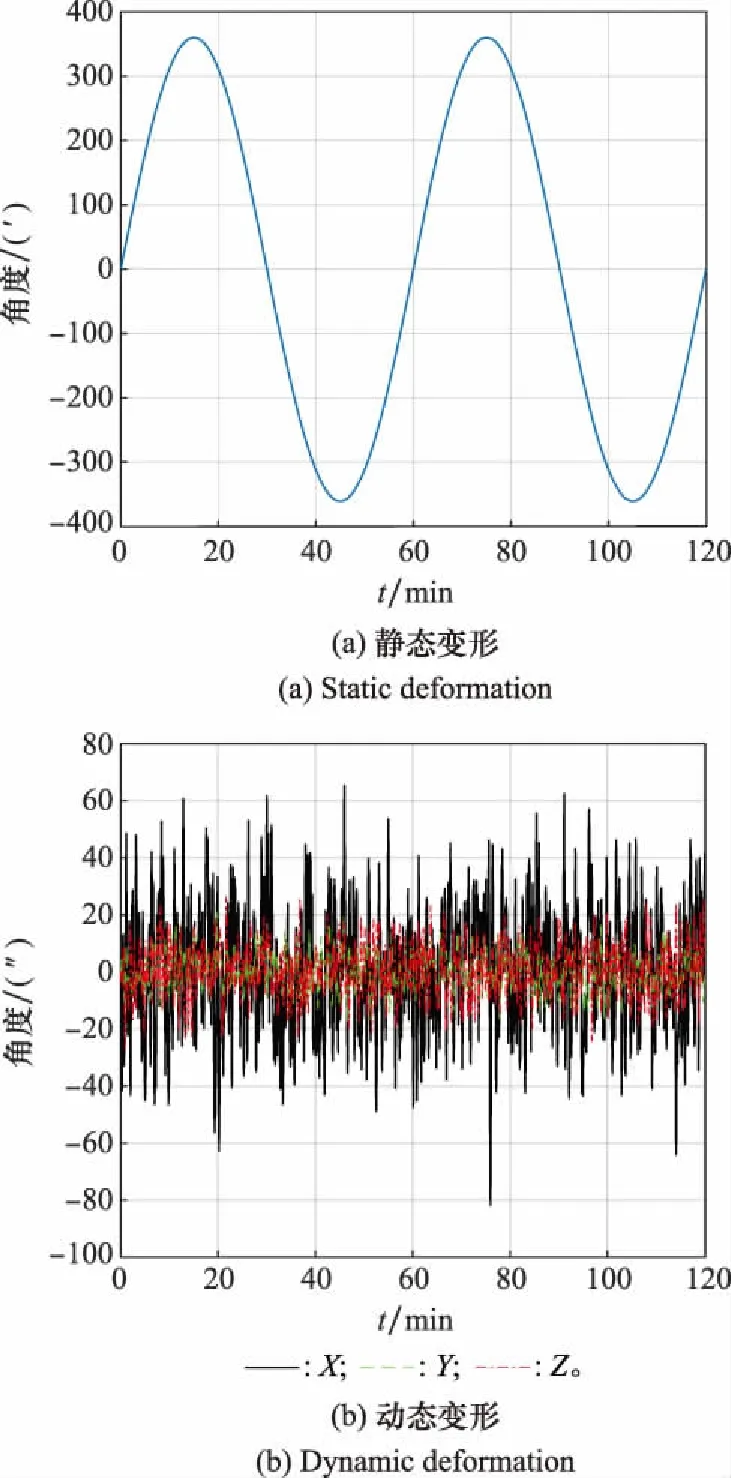
图1 船体变形角示意图

2.2 实验与分析

本节通过两种典型的非高斯噪声来对比验证MCKF、MAKF、TAKF、MCCKF等4种滤波器的船体变形角估计性能:冲击噪声和高斯混合噪声,又称强拖尾噪声。此外,为确保角度估计长时间的收敛稳定性,整个滤波时间较长;且为避免角度估计结果的偶然性,所有实验的RMSE值均采用50次蒙特卡罗独立重复实验计算其均值,并统一从滤波稳定之后开始计算(5 min)。

2.2.1 实验一: 冲击噪声

假设量测量Z每个通道均受到如下非高斯分布的剧烈冲击噪声(单位:rad/s):

Δvshot=5×10-4,t≥100 s

(28)

该冲击信号次数设置为1 000次,且随机施加给系统。单通道噪声示意图如图2所示,4种滤波器各轴的变形角跟踪曲线和误差曲线分别如图3和图4所示。

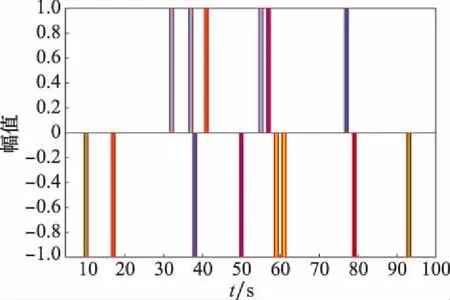
图2 冲击噪声

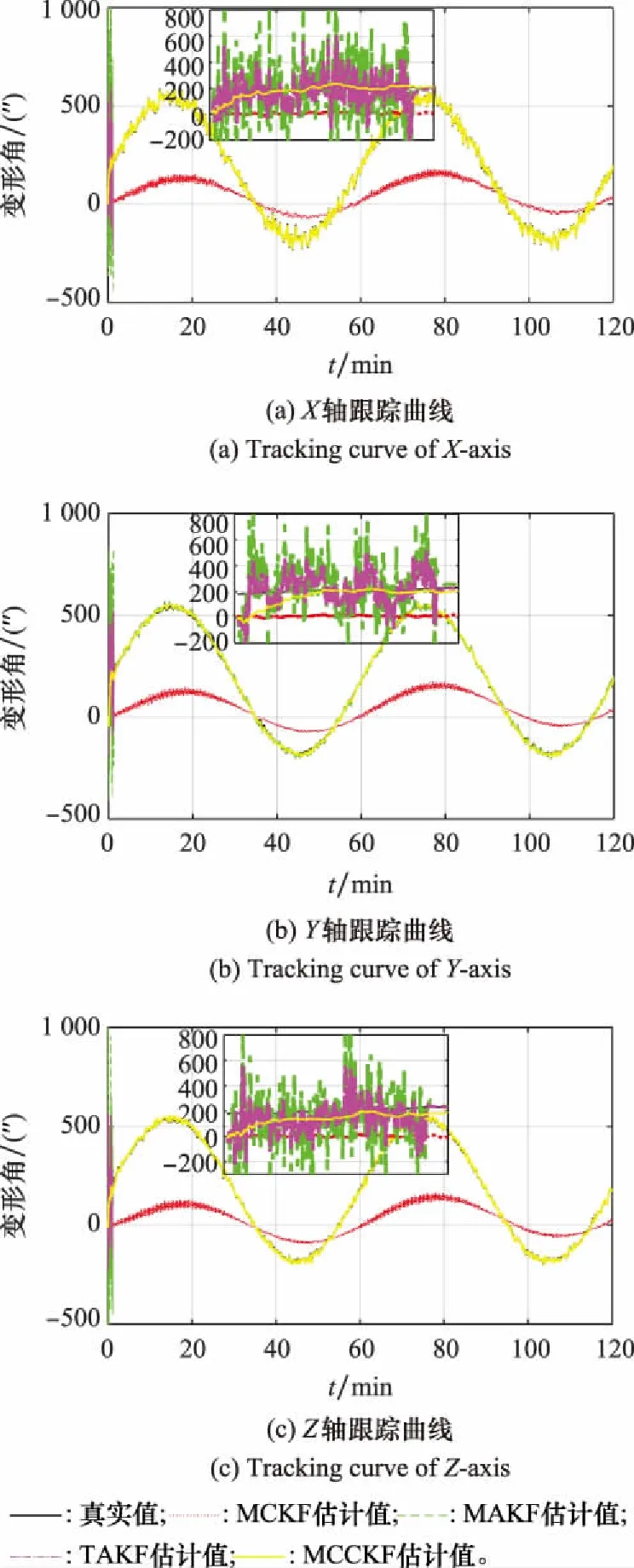
图3 变形角跟踪曲线(冲击)

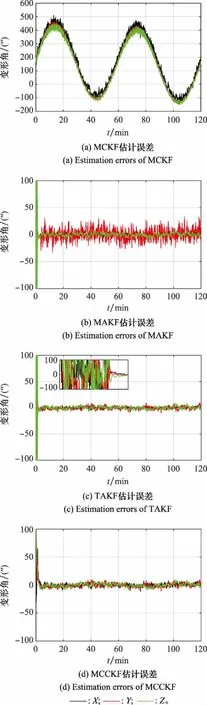
图4 变形角估计误差(冲击)

各轴变形角估计误差的RMSE值如表2所示。

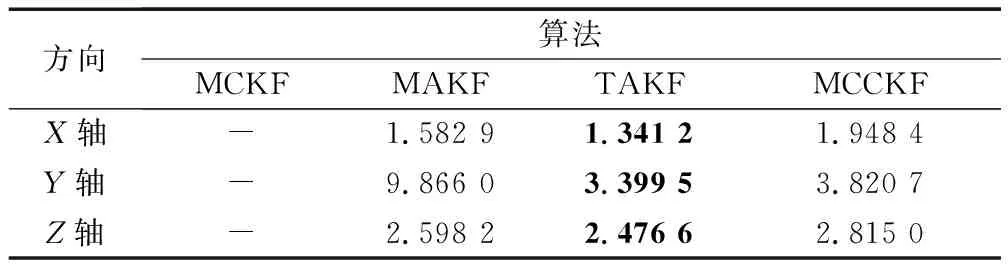
表2 船体变形估计RMSE(冲击)

从图3和图4可以看出,在系统受到随机的冲击噪声下,传统的MCKF滤波效果最差,在规定时间内甚至无法收敛,这是因为长时间的滤波误差积累导致发散;MAKF可以收敛,但由于自适应因子的引入时机可能有误,导致个别通道(横扭角)状态估计误差跳动范围大,稳定性较差;TAKF解决了这一问题,但滤波开始3 min内角度跟踪误差曲线出现巨大跳变;而MCCKF在稳定性上显著优于前者,但快速收敛之后抗随机噪声干扰的能力要稍弱于自适应滤波器。根据表2显示,TAKF在精度上具有微弱优势,稳定后的RMSE值要略大于前者0.4″,这在更为强调稳定性的工程上几乎忽略不计。可以认为,在收敛精度满足要求时,可以选择MCCKF以期实现更稳定、更快的变形测量。

2.2.2 实验二: 混合噪声

高斯混合噪声,即将两种非零均值、非高斯分布的噪声混合,同样施加给量测信息(均值单位:rad/s;方差单位:(rad/s)2),表达式为

(29)

式中：N(·，·)为正态分布。为方便起见,其中相关参数设置下:

(30)

(31)

不同于实验一随机施加的冲击噪声,混合噪声存在于整个实验过程,其单通道示意图如图5所示,各滤波器的变形角跟踪曲线如图6所示。

图5 混合噪声

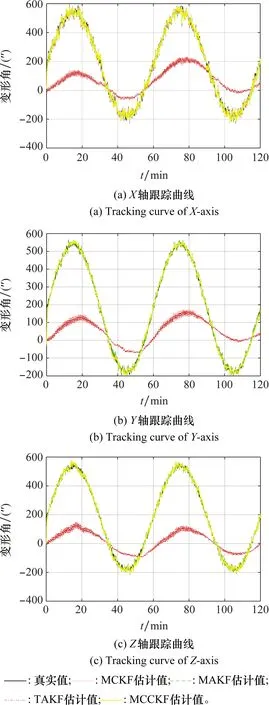
图6 变形角跟踪曲线(混合)

相应的误差收敛曲线也给出,如图7所示。

图7 变形角估计误差(混合)

收敛曲线表明自适应滤波器和MCCKF均可快速达到稳定状态,但明显可见,MCCKF误差更小,波动阈值要小于MAKF和TAKF。

各轴变形估计的RMSE结果如表3所示。

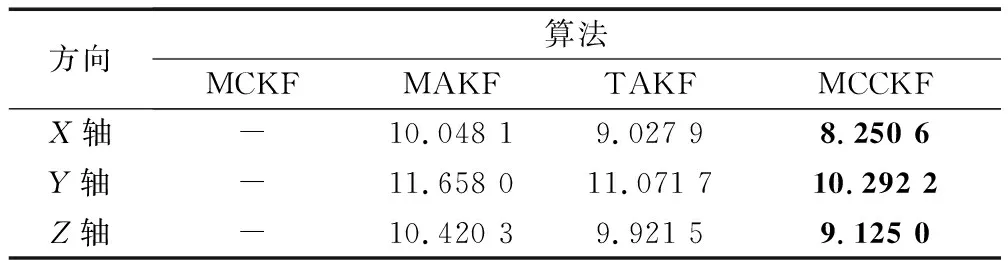
表3 船体变形估计RMSE(混合)

混合噪声扰动下,与实验一不同的是,此时MCCKF的收敛精度要高于TAKF,这是因为混合噪声在整个滤波过程均存在,自适应滤波器在这种情况下不具备自适应抗随机扰动优势,而MAKF不存在判断失误的情况因此并未出现误差跳变的情形。从实验结果可以看出,MCCKF在收敛精度和稳定性上也要比MAKF、TAKF优1″左右。此外,当逐步加大噪声幅值,MCCKF的RMSE值要比TAKF小至数个角秒,表明强非高斯环境下,MCCKF具备更明显的优势。

2.2.3 实验三: 常值静态变形角

此外,针对船体静态变形角建模为常值的情形,进一步验证MCCKF滤波算法的鲁棒性。静态变形角大小均设置为0.1°,以冲击噪声为例,静态变形角示意图、变形角跟踪曲线分别如图8和图9所示。

图8 常值静态变形角

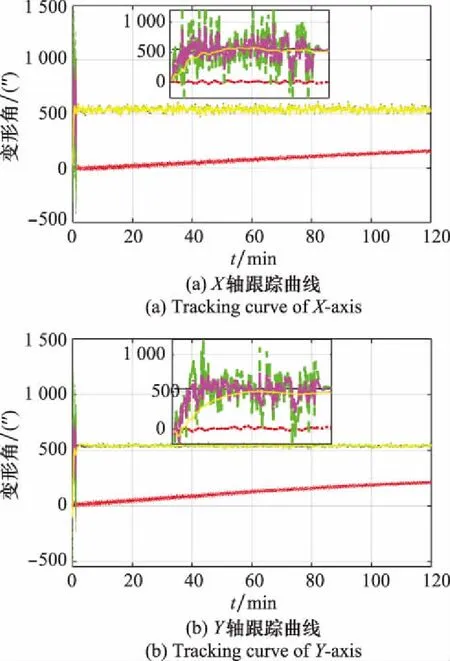
图9 变形角跟踪曲线(常值静态变形角+冲击噪声)

相应的误差收敛曲线、变形角估计误差的RMSE值分别如图10和表4所示。

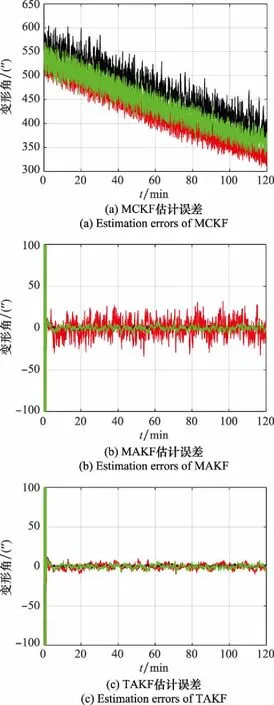
图10 变形角估计误差(常值静态变形角+冲击噪声)

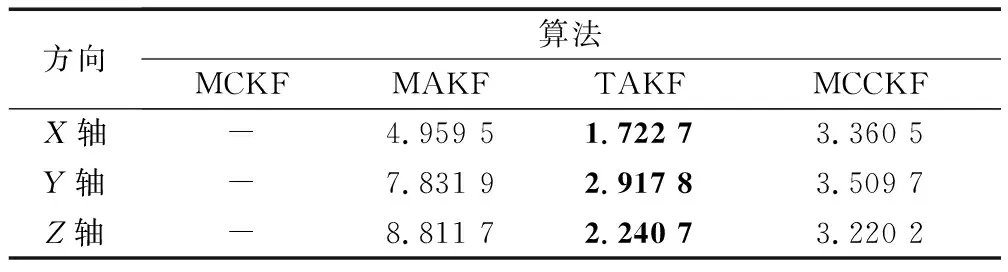
表4 船体变形估计RMSE

当静态变形角建模为常值情形时,实验结果再次验证了实验一的结论,但MCKF有收敛趋势,延长滤波时间或可收敛。实验表明本文介绍的MCCKF收敛性能始终优于MCKF,且对不同的变形测量模型也具有较好的鲁棒性。

此外,当加大实验三的冲击噪声频率次数,MCCKF的RMSE值与TAKF差距越来越小,再次验证MCCKF相对于自适应滤波器,对强非高斯环境滤波更加具备优势。

最后,从算法本身来讲,基于权重矩阵的MCCKF相较于两种自适应滤波器MAKF、TAKF,迭代算法简洁和直观,无需设置判断语句,更方便编程。并且,后者涉及自适应渐消因子缩放系数的选取,选取结果直接影响自适应滤波性能。考虑到最大熵滤波器对随机外扰、强非高斯均具备不亚于自适应滤波器的性能,本文介绍的MCCKF通用性也更强。

3 结 论

本文介绍了一种基于最大熵准则和权重矩阵核函数的改进卡尔曼滤波器,并成功应用于非高斯白噪声环境下的船体变形测量。重点介绍了基于最大熵的卡尔曼滤波器算法迭代公式,并对比两种典型的自适应滤波器和传统最大熵滤波器来验证MCCKF滤波性能。各项实验的结果证实,新算法在滤波精度和收敛速度上满足相关收敛指标前提下,还可更好地解决噪声模型失配和非高斯噪声环境下的变形角估计问题,且在不同实验条件下仍保持良好的鲁棒性。此外,算法不仅可直接应用于复杂干扰、噪声建模失准环境下的光纤陀螺组件船体变形测量问题,对于其他用到卡尔曼滤波算法的实际工程问题也具有一定的指导意义,如运载体跟踪、导航和定位,组合导航的组合滤波算法等。