基于余弦幅度加权的低旁瓣多相位分段调制干扰方法

王宏艳, 降佳伟, 蒲 娟, 吴彦鸿, 冉 达

(1.航天工程大学航天信息学院, 北京 101416; 2.航天工程大学电子与光学工程系, 北京 101416;3.西昌卫星发射中心, 四川 西昌 615099; 4.北京宏锐星通科技有限公司, 北京 100085)

0 引 言

随着现代雷达技术的不断发展,线性调频(linear frequency modulation, LFM)信号和脉冲压缩(pulse compression, PC)技术广泛应用于各种先进体制雷达及雷达应用中[1]。LFM信号和PC技术的应用不仅能够解决雷达探测威力和分辨能力之间的矛盾,还能够有效增强雷达抗压制式干扰能力,对雷达干扰提出了新挑战[2]。

对雷达实施干扰从而阻止雷达获取目标信息是雷达对抗的主要目的。根据干扰效果的不同,干扰可以分为欺骗式干扰和压制式干扰。欺骗式干扰通过对接收到的雷达信号调制错误的位置、速度、散射特性等信息生成虚假目标干扰信号,诱使对方雷达做出错误判决[3-9]。欺骗式干扰包括多种干扰样式,例如移频调频干扰[10-12]、间歇采样干扰[13-14]、运动调制干扰[15-17]、卷积调制干扰[18-19]等。然而,随着雷达分辨能力提高,高分辨率的虚假目标信号生成受到侦察参数精度以及计算复杂度的影响,实施难度、实施精度要求较高,并且无法遮盖真实目标信息[20-22]。压制式干扰通过对接收到的雷达信号进行噪声调制或部分相干调制,再放大转发,使得真实目标淹没在压制式干扰中,阻止雷达获取目标信息[23-25]。与欺骗式干扰相比,压制式干扰通常对侦察参数精度要求较低,计算复杂度较低,实施难度和精度要求较低,常用来进行要地防护[26-27]。然而,压制式干扰通常范围较大,功率需求高,容易被敌方发觉并采取相应的抗干扰措施。

多相位分段调制(multiple phases sectionalized modulation, MPSM)干扰是一种部分相干干扰,通过将接收到的信号在时域内分为多段,并在每段调制不同的相位得到[28]。与传统非相干压制式干扰相比,MPSM干扰能够通过控制参数实现对干扰范围的有效控制,还能够获得部分脉冲压缩处理增益,有效降低了干扰功率需求[29-30]。但是MPSM干扰仍存在较强的旁瓣,容易暴露目标和干扰位置信息。针对这个问题,本文提出一种基于余弦幅度加权的MPSM干扰方法[31-33]。通过对MPSM干扰的每个分段进行余弦幅度加权,抑制干扰信号旁瓣,实现隐蔽干扰效果[34-36]。

论文首先对基于余弦幅度加权的MPSM干扰进行建模和分析,之后对基于余弦幅度加权的MPSM干扰参数的影响进行分析,最后通过计算机仿真验证所提方法的可行性和有效性。

1 基于余弦幅度加权的MPSM干扰原理

1.1 MPSM干扰原理

MPSM干扰是将接收到的雷达信号在时域上分成若干段,并在每个分段上调制不同相位得到的干扰方式。MPSM干扰产生的示意图如图1所示。

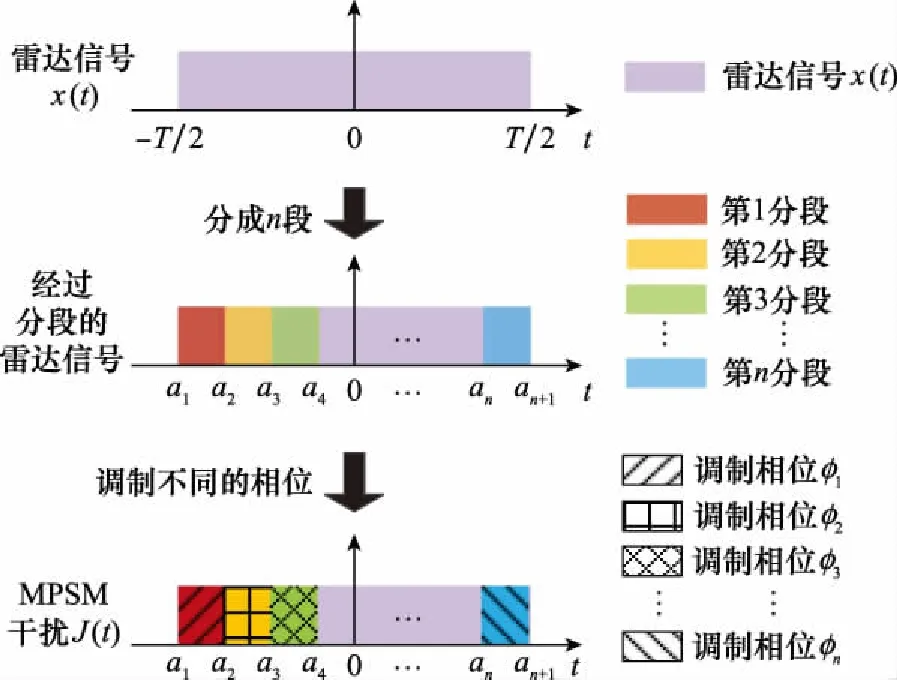
图1 MPSM干扰示意图

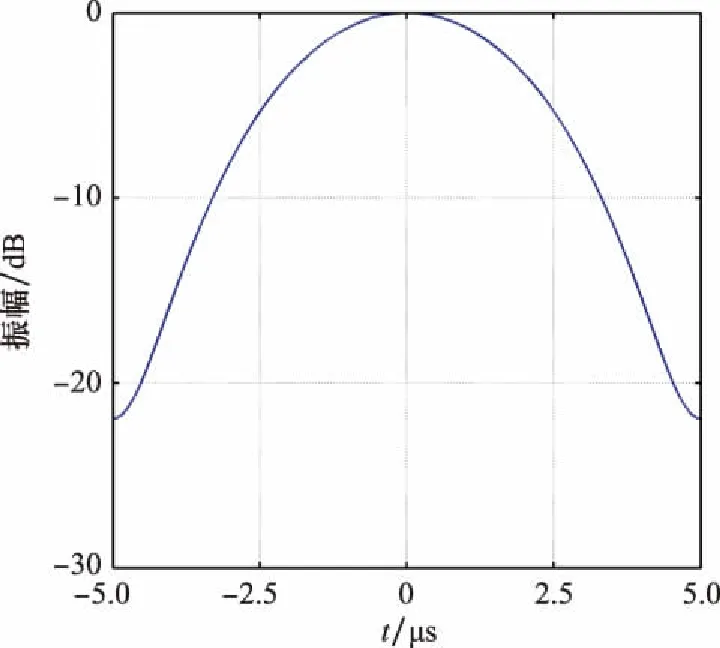
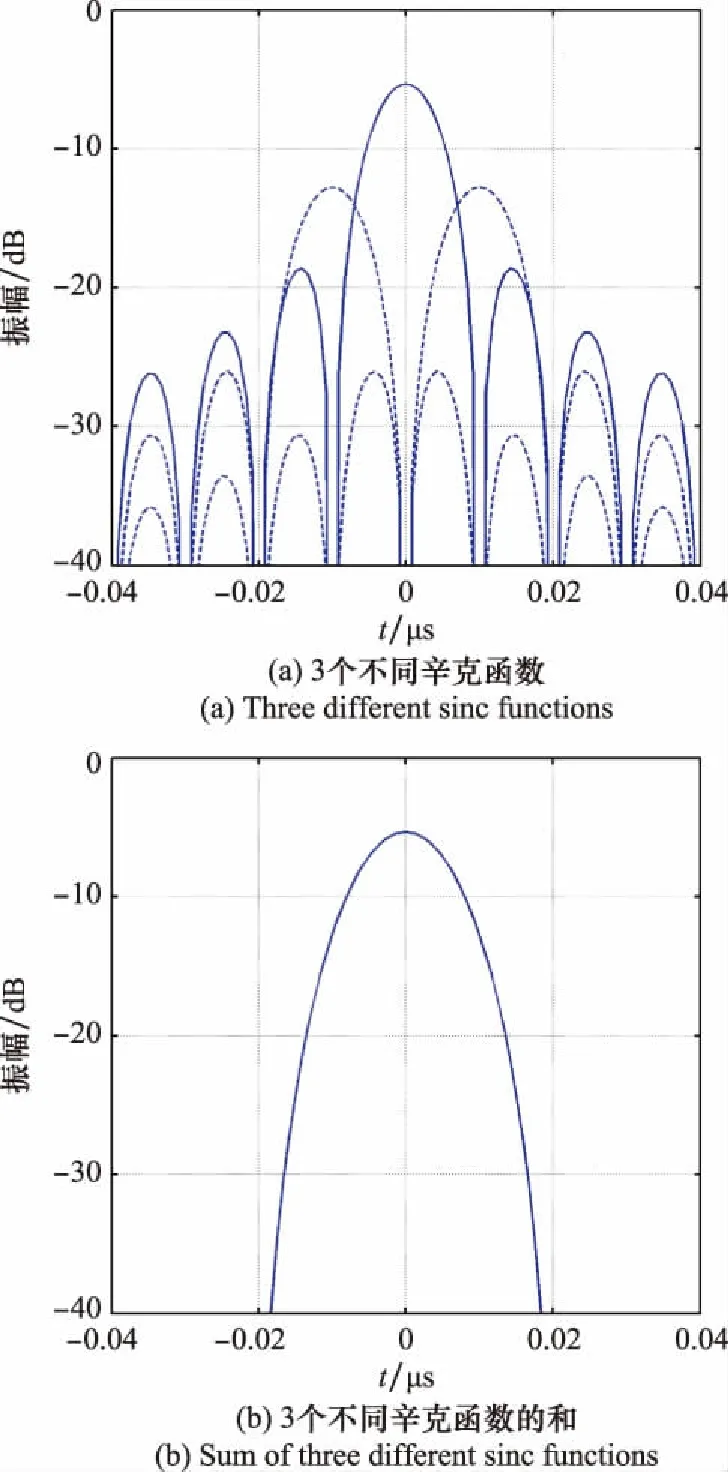
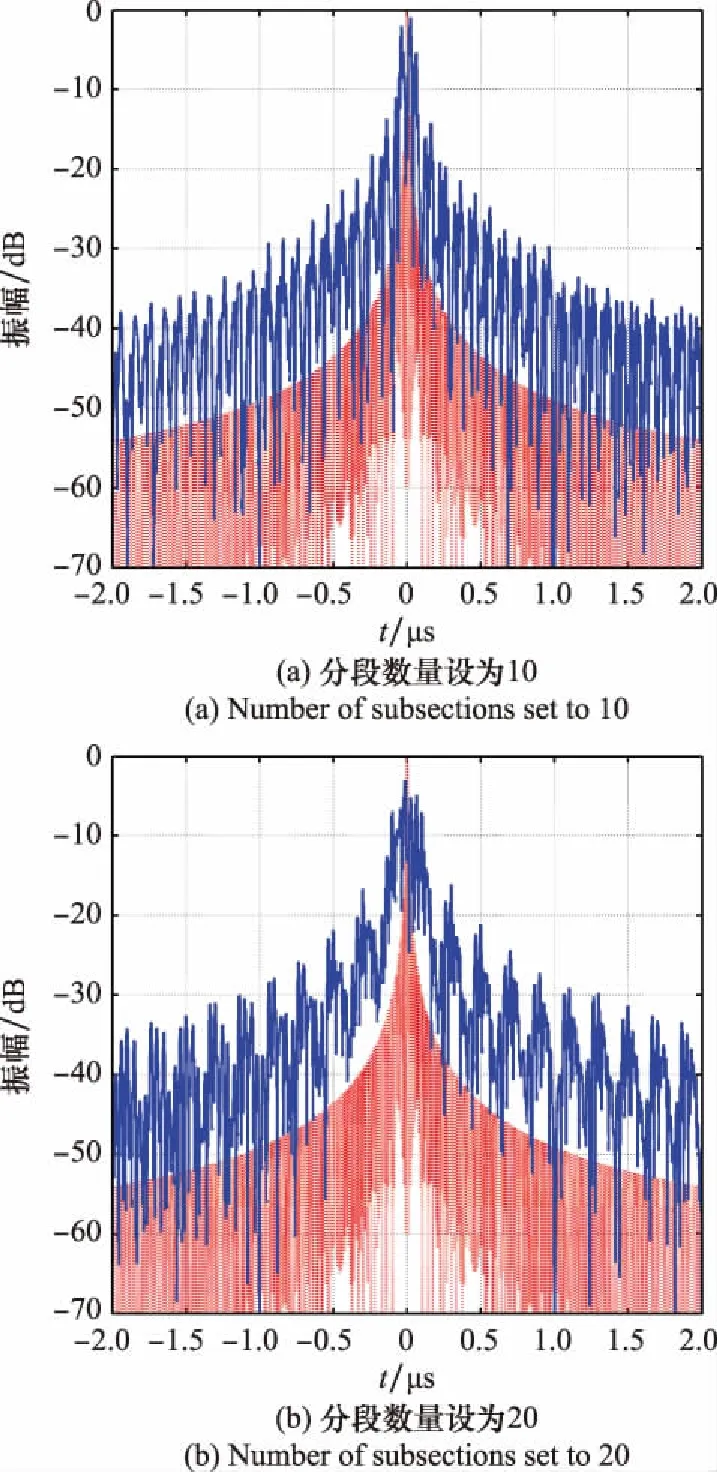
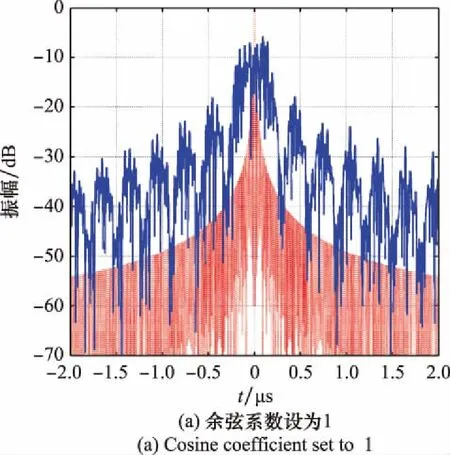
图1中,x(t)表示接收到的雷达信号,为LFM信号,T为脉冲宽度,n表示分段数量,ai与ai+1分别表示第i个分段的起点和终点,-T/2≤ai

(1)

式中:rect(t)为矩形函数;K为LFM信号调频率;ε(t)为阶跃函数。由式(1)可知,J(t)可以表示为x(t)与MPSM信号p(t)的乘积,则p(t)表达式如下:

(2)

MPSM信号p(t)可以表示为不同分段调制信号的和,如下所示:

(3)

其中,pi(t)的表达式为

pi(t)=[ε(t-ai)-ε(t-ai+1)]exp(jφi)

(4)

同理,J(t)也可以表示为不同分段调制干扰信号的和,如下所示:

(5)

式中:Ji(t)表示第i分段对应的调制干扰信号,其表达式如下:

[ε(t-ai)-ε(t-ai+1)]exp(jφi)

(6)

则第i分段对应的调制干扰信号Ji(t)的脉冲压缩结果可以表示为

Si(t)=Ji(t)*h(t)

(7)

式中:*表示卷积运算,h(t)为匹配滤波器函数,为x(t)的复共轭形式。式(7)经过计算,结果如下所示:

Si(t)=exp(jφi)exp(-jπKt2)·

{rect{[t-(ai+ai+1-T)/2]/(ai+1-ai)}·

exp[jπKt(t+T/2+ai)]·(t+T/2-ai)·

sinc[Kt(t+T/2-ai)]+rect{[t-(ai+ai+1)/2]/

(ai-ai+1+T)}exp[jπKt(ai+ai+1)]·(ai+1-ai)·

sinc[Kt(ai+1-ai)]+rect{[t-(ai+ai+1+T)/2]/

(ai+1-ai)}exp[jπKt(t-T/2+ai+1)]·

(ai+1-t+T/2)sinc[Kt(ai+1-t+T/2)]}

(8)

式中:sinc为辛克函数,sinc(t)=[sin(πt)]/πt。由式(8)可知,Si(t)的表达式为分段函数形式,并且较为复杂,不利于对干扰结果进行计算和分析。通过对式(8)进行分析可知,Si(t)的峰值位于第二段分段函数内,其余两段分段函数的值较小,可以忽略。因此,第i分段对应的调制干扰信号的脉冲压缩结果Si(t)可以简化为如下形式:

Si(t)≈(ai+1-ai)sinc[Kt(ai+1-ai)]exp(jφi)·

exp(-jπKt2)exp[jπKt(ai+ai+1)]

(9)

由式(9)可知,MPSM干扰的脉冲压缩结果S(t)可以表示为如下形式:

exp(-jπKt2)exp[jπKt(ai+ai+1)]}

(10)

由式(10)可知,MPSM干扰的脉冲压缩结果S(t)可以表示为具有不同调制相位、不同幅度系数和不同主瓣宽度的sinc函数的和。如无特别说明,此处主瓣宽度是指主瓣零点宽度。

1.2 余弦幅度加权原理

余弦幅度加权函数是最常用的时域加权函数之一。余弦幅度加权函数[26]可以表示为

(11)

式中:α为余弦系数,0.5≤α≤1。当α=0.5时,余弦幅度加权函数为汉宁加权函数,当α=0.54时,为汉明加权函数,如图2所示。

图2 余弦幅度加权函数(余弦系数为0.54)

经过余弦幅度加权的雷达信号如下所示:

(12)

则经过余弦幅度加权的雷达信号xw(t)的脉冲压缩结果可以表示为

Sw(t)=xw(t)*h(t)

(13)

式(13)经过计算可得

(14)

由式(14)可知,Sw(t)可以表示为3个具有不同加权系数和偏移量的sinc函数的和,加权系数与余弦系数α有关,偏移量为固定值,分别为-1/(KT)和1/(KT)。由LFM信号性质可知,K=B/T,则偏移量可以表示为-1/B和1/B。式(14)中,sinc函数主瓣宽度经过计算为2/B。具有偏移量的sinc函数峰值分别位于没有偏移的sinc函数主瓣两端,如图3所示。

图3 经过余弦幅度加权的信号脉冲压缩结果(余弦系数为0.54)

图3(a)中,实线函数为没有偏移的函数,虚线为具有偏移的函数,图3(b)为3个函数的叠加结果。由图3可知,具有偏移量的函数位于没有偏移的函数的主瓣和旁瓣之间,将函数主瓣与第一旁瓣结合,从而实现抑制旁瓣,展宽主瓣的效果。余弦系数越小,具有频移的函数幅度越大,此时旁瓣抵消效果越好,主瓣展宽越严重。

1.3 基于余弦幅度加权的多相位分段调制干扰脉冲压缩结果

由第1.2节可知,对LFM信号进行余弦幅度加权能够抑制旁瓣,展宽主瓣。当对MPSM干扰信号进行余弦幅度加权时,由于MPSM干扰信号可以等效为分段调制干扰信号的和。因此,需要对每段调制干扰信号分别进行余弦幅度加权。则MPSM干扰信号经过余弦幅度加权后可以表示为

(15)

式(15)经过脉冲压缩处理后的结果可以表示为

exp(jφi)exp(-jπKt2)exp[jπKt(ai+ai+1)]+

(16)

由式(16)可知,基于余弦幅度加权的MPSM干扰可以表示具有不同加权系数、不同偏移的MPSM干扰的和。其中,加权系数由余弦系数α决定,偏移量为固定值,与信号带宽B有关。由余弦幅度加权原理可知,具有偏移量的MPSM干扰可以抵消没有偏移的MPSM干扰的旁瓣,扩展其主瓣,从而生成低旁瓣的MPSM干扰。

与没有加权的MPSM干扰相比,基于余弦幅度加权的MPSM干扰可以有效降低旁瓣,并扩展主瓣干扰范围。在对LFM-PC雷达进行干扰时,不仅能够实现局部压制式干扰效果,还可以减少干扰能量泄露到旁瓣,降低被发现的概率,实现对干扰更为精准和有效的控制。

2 干扰参数效果分析

2.1 多相位分段调制干扰参数影响分析

由式(10)可知,影响MPSM干扰效果的参数主要包括分段长度情况ai+1和ai、分段数量n和调制相位情况φi。

2.1.1 分段长度

分段长度情况是指每个调制分段的时域信号长度,由MPSM干扰的定义和表达式可知,第i个调制分段的长度可以表示为

Δai=ai+1-ai

(17)

将式(17)代入式(10),则式(10)可以表示为

exp(-jπKt2)exp[jπKt(ai+ai+1)]}

(18)

由式(18)可知,分段长度情况Δai主要影响sinc函数的主瓣宽度和幅度系数。Δai越大,sinc函数主瓣宽度越窄,幅度系数越大。当所有分段长度Δai都相同时,此时,Δai=T/n,则式(18)可以表示为

exp[jπKt(ai+ai+1)]}

(19)

由式(19)可知,当所有分段长度Δai都相同时,MPSM干扰可以表示为具有sinc函数包络的形式。由于sinc函数的主瓣能量通常占信号总能量的90%以上,这意味着MPSM干扰的主要能量集中在sinc函数的主瓣宽度范围内,即sinc函数的主瓣宽度范围可以等效为MPSM干扰范围,使得MPSM干扰具有局部压制式干扰效果。

2.1.2 分段数量

由式(19)可知,MPSM干扰的sinc函数主瓣宽度为2n/B,真实目标的主瓣宽度为2/B,MPSM干扰的主瓣宽度是真实目标的n倍,其关系式如下所示:

(20)

式中:rn为MPSM干扰主瓣宽度,即MPSM干扰范围;r为真实目标的主瓣宽度。由式(20)可知,当MPSM干扰的调制分段数量n越大,则MPSM干扰范围就越大。

由式(19)可知,MPSM干扰的幅度系数为T/n,真实目标的幅度系数为T,MPSM干扰的幅度系数是真实目标的1/n,如下所示:

(21)

式中:k为真实目标的幅度系数。由式(20)可知,当MPSM干扰的调制分段数量n越大,则MPSM干扰的幅度就越小。

由信号相干性角度可知,当调制分段数量n越大,意味着MPSM干扰信号与雷达信号的相干性越弱,此时,失配程度就越大,则干扰信号的展宽量就越大,幅度下降也就越明显。通过对MPSM干扰的分段数量n分析,MPSM干扰范围可以认为与分段数量n成正比,MPSM干扰幅度可以认为与分段数量n成负相关。这些特性使得MPSM干扰的局部压制式干扰效果具有很强的可控性,通过控制分段数量n,可以实现对MPSM干扰范围和干扰幅度的有效、灵活控制。

2.1.3 调制相位

由式(19)可知,当所有分段长度Δai都相同时,式(19)可以简化为如下形式:

(22)

式(22)经过整理可得

(23)

由式(23)可知,调制相位φi主要影响求和项的结果。对于某一时刻t,不同调制分段对应的exp[jπKTt(i/n)]项中,相位值分布为等差数列形式。特别的,当调制相位φi都相同时,MPSM干扰与真实目标信号幅度完全相同,只存在一个固定的相位差。当调制相位φi随机分布时,此时,式(23)中求和项受到调制相位随机性的影响,使得求和项的结果呈现一定的随机性,表现在波形上即类似噪声的干扰波形。

当MPSM干扰的分段长度Δai都相同,调制相位φi随机分布时,MPSM干扰将会在主瓣范围内产生类似噪声的干扰效果,能够对目标或区域产生局部压制式干扰效果。

2.2 余弦幅度加权参数影响分析

由式(14)可知,影响加权系数的参数主要为余弦系数α。特别的,当α=1时,此时为矩形加权函数,式(14)结果可以简化为

Sw(t)=Tsinc(KTt)

(24)

由式(24)可知,余弦系数为1时,加权函数为矩形函数,加权结果与真实目标信号相同,此时频移分量的加权系数为0。

当0.5≤α<1时,式(13)可以表示为

Sw(t)=A(t)+B(t)+C(t)

(25)

其中,

(26)

B(t)与C(t)的峰值分别位于A(t)主瓣两侧,且B(t)与C(t)的主瓣宽度与A(t)相同,则Sw(t)的主瓣宽度由A(t)、B(t)与C(t)共同决定。A(t)越大,B(t)与C(t)越小,Sw(t)旁瓣抑制效果越差,主瓣展宽越小,A(t)越小,B(t)与C(t)越大,Sw(t)旁瓣抑制效果越好,主瓣展宽越大。由式(25)和式(26)可知,当余弦系数α越小,A(t)的幅度就越小,B(t)和C(t)的幅度就越大,则旁瓣抑制效果就越好,但是主瓣展宽就越严重。

2.3 基于余弦幅度加权的多相位分段调制干扰效果分析

由式(16)可知,基于余弦幅度加权的MPSM干扰能够产生局部压制式干扰效果。由第2.1节与第2.2节分析可知,干扰效果受到分段长度情况ai+1和ai、分段数量n、调制相位φi和余弦系数α的共同影响。当分段长度Δai都相同,调制相位φi随机分布时,干扰范围与分段数量n成正比,分段数量越大,干扰范围越大,干扰旁瓣幅度与余弦系数α成负相关,余弦系数越小,干扰旁瓣越小。通过对基于余弦幅度加权的MPSM干扰参数进行控制,不仅能够产生具有范围可控特性的局部压制式干扰效果,还能够有效抑制干扰旁瓣,降低干扰被发现的概率,并且进一步增强干扰的可控性。

3 仿真验证

3.1 仿真参数设置

针对上文理论分析,将对MPSM干扰以及基于余弦幅度加权的MPSM干扰的局部压制式干扰效果的有效性和可控性进行仿真验证和对比。基础仿真参数设置如表1所示。

表1 仿真参数设置

3.2 多相位分段调制干扰效果仿真验证

本节对MPSM干扰结果进行仿真。设置MPSM干扰的分段长度均相同,分段数量分别为10、20、30、40,调制相位为随机相位,干信比(jamming signal ratio, JSR)为5 dB。则MPSM干扰仿真结果如图4所示。如无特别说明,本节所指主瓣宽度均为主瓣零点宽度。

图4 不同分段数量条件下的MPSM干扰脉冲压缩结果

由图4可知,MPSM干扰能够对LFM-PC雷达产生局部压制式干扰效果。由图4中可知,当分段长度均相同时,MPSM干扰存在一个明显的主瓣零点宽度范围,并且干扰能量主要集中在该主瓣零点宽度范围内,通过合理设置干扰机输出功率,能够对目标形成有效的压制式干扰效果。随着分段数量的增加,干扰的主瓣范围也在增加,由图4中仿真结果计算可知,当分段数量分别为10、20、30、40时,MPSM干扰的主瓣范围仿真结果分别为0.191 μs、0.41 μs、0.601 μs、0.811 μs,理论推导结果分别为0.201 μs、0.401 μs、0.601 μs、0.801 μs,仿真结果与理论推导基本一致。由图4中可以看出,随着分段数量的增加,MPSM干扰幅度逐渐降低,并且在MPSM干扰的主瓣范围内,由于调制相位随机分布,使得干扰效果与噪声干扰类似。仿真结果与理论推导相一致,验证了MPSM干扰的局部压制式干扰效果的正确性和有效性。

3.3 基于余弦幅度加权的多相位分段调制干扰效果仿真验证

本节首先对余弦幅度加权函数进行仿真验证。分别对余弦系数为1、0.75、0.54、0.5情况下的余弦幅度加权函数进行仿真。仿真结果如图5所示。

图5 不同余弦系数条件下的目标信号脉冲压缩结果

图5(a)为余弦系数为1时真实目标回波的脉冲压缩结果,即相当于未经过余弦幅度加权的结果,通过计算可知,此时主瓣宽度为0.02 μs,峰值旁瓣比(peak side lobe ratio, PSLR)为-13.45 dB,与图5其他结果相比,此时主瓣最窄,但是PSLR最高。图5(b)为余弦系数为0.75时的仿真结果,图中目标回波主瓣宽度约为0.025 μs,与未加权结果相比,主瓣展宽40%,PSLR约为-21.21 dB,与未加权结果相比,PSLR下降7.76 dB。图5(c)为余弦系数为0.54时的仿真结果,此时加权函数为汉明加权函数,目标主瓣宽度约为0.04 μs,展宽100%,PSLR约为-42.64 dB,下降29.19 dB。图5(d)中余弦系数为0.5,此时为汉宁加权函数,目标主瓣宽度约为0.04 μs,展宽100%,PSLR为-31.51 dB,下降18.06 dB。由仿真结果可知,加权系数越小,旁瓣抑制效果越好,主瓣展宽越严重,当加权系数为0.54时,此时旁瓣抑制效果最好。

之后,对不同余弦系数条件下的MPSM干扰结果进行仿真。设置MPSM干扰分段长度均相同,分段数量为30段,调制相位为随机相位,余弦系数分别为1、0.75、0.54和0.5,JSR为5 dB。仿真结果如图6所示。

图6 不同余弦系数时余弦幅度加权的MPSM干扰脉冲压缩结果

图6所示为不同余弦系数条件下基于余弦幅度加权的MPSM干扰脉冲压缩仿真结果。由图6(a)可知,余弦系数为1时,即未经余弦幅度加权的MPSM干扰主瓣宽度为0.60 μs,干扰的PSLR(对MPSM干扰来说,即最强旁瓣范围内峰值与主瓣范围内峰值幅度的比值)为-12.19 dB。图6(b)中,余弦系数为0.75,干扰峰值幅度下降2.16 dB,干扰主瓣宽度约为0.74 μs,展宽23%,干扰PSLR约为-20.37 dB,下降8.2 dB。图6(c)中,余弦系数为0.54,干扰峰值幅度下降4.51 dB,干扰主瓣宽度约为1.26 μs,展宽为110%,干扰PSLR约为-37.47 dB,下降25.28 dB。图6(d)中,余弦系数为0.5,干扰峰值幅度下降5.04 dB,干扰主瓣宽度约为1.21 μs,展宽为102%,干扰PSLR约为-31.55 dB,下降19.36 dB。

由仿真结果可知,对比图6(a)与图6其余仿真结果可知,基于余弦幅度加权的MPSM干扰能够有效抑制干扰旁瓣,并且能够扩展主瓣。综合仿真结果可知,当加权系数α为0.54时,基于余弦幅度加权的MPSM干扰旁瓣抑制效果最好,PSLR为-37.47 dB,此时旁瓣影响可以忽略,干扰能量可以认为只存在于经过扩展的主瓣范围内,约为4n/B,此时干扰PSLR相比没有加权时下降27.47 dB,干扰峰值幅度下降4.51 dB,PSLR下降幅度远高于峰值下降幅度,说明干扰能量分布在主瓣范围内,基本不受干扰旁瓣影响。本文所提基于余弦幅度加权的MPSM干扰方法可以实现干扰能量范围的精准、有效控制,基本消除干扰旁瓣的影响。

4 结 论

MPSM干扰可以对LFM-PC雷达产生局部压制式干扰效果,但是MPSM干扰存在较强的旁瓣,不仅造成干扰能量的泄露,还削弱了干扰实施的隐蔽性。针对这个问题,论文基于时域加窗抑制旁瓣的思想,提出一种基于余弦幅度加权的MPSM干扰方法,该方法首先对雷达信号进行多相位分段调制,之后在时域内对干扰信号的每个分段进行余弦幅度加权,从而产生基于余弦幅度加权的MPSM干扰信号。该干扰信号经过脉冲压缩后,可以对LFM-PC雷达形成低旁瓣的局部压制式干扰效果,有效减少干扰能量泄露到旁瓣,进一步增强了干扰实施的隐蔽性。仿真验证结果表明,当余弦系数为0.54时,此时旁瓣抑制效果最好,此时干扰主瓣范围约为4n/B,主瓣范围内能够产生类似噪声的压制式干扰效果。所提方法不仅能够实现对目标的有效保护,还为局部压制式干扰的研究提供了新思路。