对机载预警雷达STAP的慢时调频干扰方法

陈小舟, 邢庆君, 张立东

(中国人民解放军93209部队, 北京 100085)

0 引 言

空时自适应处理空时自适应处理(space-time adaptive processing,STAP)理论自提出以来,引起学术界的强烈兴趣[1-3]。理论和仿真证明,在均匀或部分均匀的信号环境中,即使存在信号失配,这类空时域多通道检测算法仍然具备很强的适应能力,能较准确地估计干扰、杂波和噪声的协方差矩阵[4-6]。随着STAP广泛运用于机载雷达,对其干扰方法也逐渐引起人们的重视。

STAP现行主要干扰方法有两类：自由度消耗和非均匀干扰。自由度消耗的思想是通过分布式干扰源等方式从多个方位-多普勒维度进行干扰,当STAP无法提供足够自由度对消干扰时,性能将显著下降[1]。可是这种分布式干扰源的方式依赖于多个干扰源间的目标协同,而受地形、通信等环境局限,实现难度较大。文献[7-8]提出将宽带干扰信号投向地面并散射到目标雷达,产生的干扰脉冲将占据大量空时自由度以消耗STAP的对消能力。然而这种方式对干扰能量利用率很低,难以达到足够的干信比,有待于进一步研究集中能量的方法。

目前主流的干扰思路是创造非均匀的环境。依距离不同,STAP处理的数据分为采样数据和待检数据两类。待检数据中的杂波干扰背景需要通过采样数据来估计。非均匀干扰就是通过在两类数据中构造差异,使采样数据无法表征待检数据的背景信号特征,从而产生干扰效果。文献[9-10]通过对脉压信号的调制和转发,在干扰目标附近产生了虚假脉冲,但不能独立设定虚假脉冲的数量和位置。文献[11]提出了构造一种迅速变化的信号环境,致使STAP无法实时估计出信号背景环境的干扰思路,但没有提出具体实现的方式。文献[12]提出了通过数字射频存储(digital radio frequency storage,DRFM)混叠延时转发建立干扰模型,有效增加了干扰脉冲的个数,但这种方法只针对采用降维STAP的3DT算法,未给出对其他算法的干扰效果。

以上都是基于快时(即一个脉冲重复间隔内的时间)产生信号,这种干扰方式存在几个问题。首先,干扰信号无法获得多普勒增益。特别是对于一些高重频、具备低截获特征的信号,通常一个相参脉冲间隔(coherent procesing interval,CPI)需要积累几十甚至上百个脉冲,积累后干信比将损失20 dB左右的损失。其次,干扰信号的频移和时移由同一个参数控制,容易相互冲突,因而无法产生大量干扰脉冲。

本文利用STAP算法的机理,提出一种基于慢时调频的干扰方法,相比之下其有以下优势:一是干扰信号可以通过多普勒积累产生较大的干信比;二是干扰脉冲的距离和多普勒速度可在快时、慢时分别调控互不冲突;三是虚假脉冲数量很多,可在真实目标周围形成假目标实现区域掩护,或在整个可探测的距离内形成大量干扰脉冲实现全距离覆盖。

1 STAP基本原理及实现方法

1.1 STAP基本流程

STAP工作之前,将整个空间分为许多探测单元,从每个探测单元前后的探测单元中估计背景杂波的空时特性,然后构造协方差矩阵并据此求出各通道加权值。假设天线阵具有N个阵元,一个CPI包含M个脉冲,STAP的具体计算流程如下。

步骤 1确定待检测单元(cell under test, CUT),明确该CUT的距离、方位。

步骤 2选取一个多普勒频率fd,并结合步骤1得到对应的空时导向矢量:

s(θ,fd)=b(fd)⊗a(θ)

(1)

式中：⊗是Kronecker运算符；b(fd)和a(θ)分别是时间、空间导向矢量,即

(2)

(3)

(4)

(5)

式中：d，λ，θ，T分别是阵元间距、波长、波前与阵列法线方向的夹角、脉冲重复周期(pulse repetition interval,PRI);N和M分别表示阵列单元数、脉冲相参积累数。

步骤 3确定取样范围。将CUT及前后若干个单元作为待保护单元,在待保护单元以外的距离单元进行背景取样,如图1所示,取样范围从xi±2到xi±(1+L/2),共L个样本。

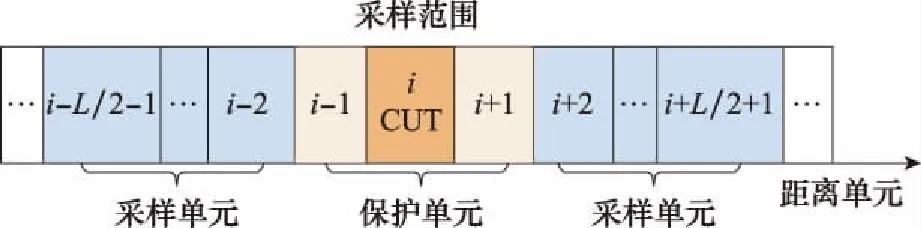
图1 STAP采样原理框图

步骤 4估计协方差矩阵。根据已采集的背景样本估计杂波协方差矩阵:

(6)

式中：(·)H表示共轭转置。

步骤 5计算权值。权重计算式为

(7)

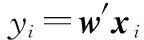
步骤 6选取下一个多普勒频率,重新执行步骤2～步骤5。

步骤 7对同一个CUT所有多普勒频率输出进行比较,输出值超出检测门限的认为有回波目标输出。

步骤 8选取下一个距离,重新执行步骤1～步骤7,直到所有的距离单元都计算完毕。

步骤 9选取下一个方位,重新执行步骤1～步骤8。

1.2 利用慢时跨周期地采样的过程分析

从第1.1节分析可知,某一个距离单元的协方差矩阵,只与这个距离单元邻近的L个距离单元有关。假设第k个方位来波信号在N元阵列中产生的响应为z(θk)∈CN×1,如果该信号的多普勒频率fd,那么整个CPI中,该信号产生的空时二维响应就是

(8)

其中:

W0=exp(j2πfdT)

2 干扰模型和分析

2.1 干扰信号表达式

假设干扰机收到的信号为E(t),那么发射的干扰脉冲可表示为每个周期干扰脉冲的叠加,即

(9)

式中：Jm(t)是第m个PRI中发射的干扰信号,可表示为

(10)

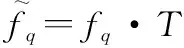
图2 慢时调频干扰原理框图

2.2 干扰脉冲相互影响分析

由式(10)可见,干扰信号由Q个脉冲组成,对每个脉冲,可以通过调整时延τq以符合掩护区域的需求,通过调整fq使每个干扰脉冲具备不同的慢时多普勒频率。如此,即使这些干扰脉冲被同时采样,也会无法被STAP对消。下面将以两个干扰脉冲为例分析说明。

(11)

由于干扰脉冲、杂波、热噪声信号相互独立,那么背景信号的协方差矩阵就是各自协方差矩阵之和,而其逆可以由求逆公式[14]展开,可得

(12)

式中：Rcn=Rc+Rn为杂波、噪声协方差矩阵之和；I表示单位矩阵。

在式(12)中,定义：

(13)

系数κ表达式为

(14)

将式(12)代入式(7)计算权重,待检脉冲产生的输出信号应为

(15)

功率可以表示为

(16)

将式(13)代入式(16)得

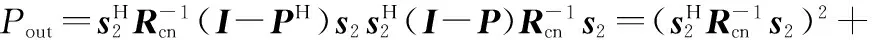
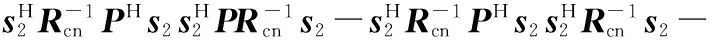
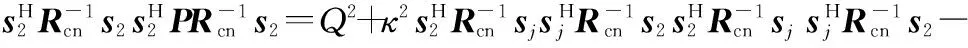
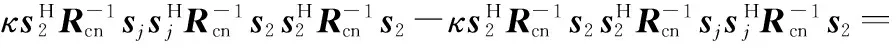
Q2+κ2|q|4-2κ|q|2=(Q-κ|q|2)2

(17)

式中：

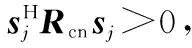
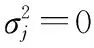
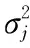
(18)

式中:aj和a2分别是样本脉冲和待检脉冲的空间导向矢量,在本干扰模型中已经确定为常数;bj和b2分别是两个脉冲的时间导向矢量。根据式(3)的定义可得

(19)

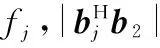
2.3 两种场景下构造频率唯一性条件的方法

通过以上分析,可以利用慢时调频唯一性原理,通过合理分配采样区间内脉冲的多普勒频率,形成无法被STAP滤除的干扰脉冲串,满足不同场景的需求。

(1)区域精确掩护。当目标周围集中出现大量干扰信号时,相应区域的杂波噪声背景会被抬高,真实目标被隐藏,即形成所谓的有源隐身或隐蔽干扰。如图3(a)所示,干扰脉冲全部集中在目标回波附近的区域。为方便叙述,假设待掩护区域内等间距地设置Q个干扰脉冲,相邻脉冲间隔p个距离单元,那么干扰脉冲共覆盖pQ个距离单元。在区域精确掩护场景中STAP采样数L>pQ。

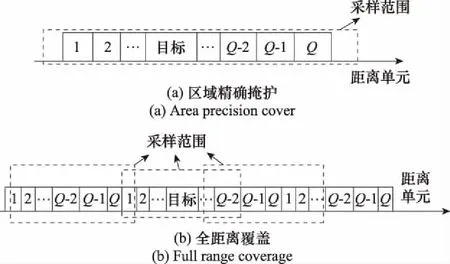
图3 两种干扰应用场景示意图

(2)全距离覆盖。在掩护多个目标时,有时需要在大范围内,甚至整个探测范围内都布满干扰脉冲。这种场景下,由于计算能力、杂波环境瞬变等因素制约,STAP只能采样一部分干扰脉冲,如图3(b)所示。此时可以设置循环多普勒数列,即将干扰脉冲频率按照1,2,…,Q,1,2,…,Q,1,2,…的规律周期排布,即可保证每一次被采样的干扰脉冲均满足频率唯一性条件而不被对消,这样干扰脉冲就可以覆盖整个探测距离。该场景将在仿真3中进一步分析。

3 仿真分析

基本参数设置:假设飞机位于[0 km,0 km,3 km],速度为[0 m/s,93.69 m/s,0 m/s];目标位于[5 km,5 km,0 km]处,速度为[15 m/s 15 m/s,0 m/s];地面干扰机位于[7.5 km,10 km,0 km]处。预警雷达峰值功率为10 kW,发射、接收增益均为40 dB,载频为4 GHz,重频为5 kHz,距离采样率为4 MHz,脉冲积累数M为20,天线阵元数N为6。STAP采用直接矩阵求逆(simple matrix inverse, SMI)方式进行计算处理。

3.1 仿真1(基本性能)

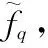
图4 20个脉冲的干扰效果

3.2 仿真2(区域精确掩护)

为了提高脉冲遮盖性,保持仿真1中各脉冲的慢时多普勒频率不变,调整脉冲时延使其密集包围在目标(第211个单元格)前后,同时随机调整各干扰脉冲幅度,形成密集脉冲串如图5(a)所示(Q=20,p=6)。经STAP处理后输出如图5(b)所示,可见回波信号被淹没在干扰中无法分辨。这里反映了本干扰的优点之一在于将时延和多普勒频率的两类参数完全分离,可以根据需要独立控制两个参数,比起其他文献中两组参量相互耦合的情形,有更强的可控性。当干扰信号数量继续增加时(比如Q=25),则干扰效果急剧下降,干扰信号全部被抑制,位于第211个距离单元的目标回波重新出现如图6所示。这是由于当干扰信号过密时,频率上相邻的两个干扰脉冲频谱交叠过多引起的。

图5 区域掩护干扰效果(Q=20,p=6)

图6 区域掩护干扰效果(Q=25,p=6)

为了说明原因,将以上两种干扰方式中:各干扰脉冲的多普勒频谱绘制出来,如图7所示(实际上干扰脉冲频谱分布在-2 500～2 500 Hz之间,为能显示细节,图7中仅显示了-1 000～1 000 Hz的脉冲频谱)。

图7 干扰脉冲的慢时频谱比较

通过比较可见,M值决定了干扰脉冲的半功率主瓣宽度值为223 Hz。当Q=20时,相邻干扰脉冲频率中心间隔(230 Hz左右)略大于其主瓣宽度(223 Hz),意味着干扰脉冲频谱交叠较少,每个干扰脉冲在多普勒域都彼此不同。而当Q=25时,相邻脉冲频率间隔(200 Hz左右)小于频谱主瓣宽度223 Hz,这说明当STAP采集到某个干扰脉冲样本的同时,也采集到其相邻干扰脉冲的大部分频率信息,以此类推多个干扰脉冲的频率被采集,导致所有干扰脉冲被对消。考虑到脉冲积累数M通常会远高于20,根据第2节和本节的分析可知,本方法可以产生的区域掩护的假目标数量也会远高于这次实验的数值。

3.3 仿真3(全距离覆盖)

实际中STAP采样数会远小于距离单元总数,可以利用第2.3节所述,通过设置循环多普勒数列,扩充假目标的数量。在上述例子中,假设采样数L不变,将脉冲间隔设为p=13,将60个干扰脉冲的多普勒频率点按照-9T/20+{1…20,1…20,1…20}×0.9T/20的规律设置,将干扰脉冲覆盖整个探测区，如图8(a)所示。由于慢时频率循环周期大于STAP采样区间,因而所有干扰脉冲都未被STAP滤除,而干扰脉冲总数比仿真2提高了3倍,如图8(b)所示,干扰效果明显。

图8 全距离覆盖的干扰效果(Q=20,p=13)

3.4 仿真4(对降维STAP的干扰效果)

同样使用仿真3的参数产生全距离干扰,对3单元自适应偏移相位中心天线和3DT两种降维STAP算法的干扰效果如图8(c)和图8(d)所示。可见,对虽然各种降维STAP使用的降维矩阵不同,但依然遵循STAP基本原理,以及对估算、对消干扰信号的流程方法,因而慢时调频对这些降维STAP算法依然能产生良好的干扰效果。

4 结 论

本文通过对STAP采样计算过程分析,从原理上和数学上提出了慢时调频干扰方法的表达式和实现方法。该方法本质上通过慢时调频,构建非均匀的信号环境,最大程度保留干扰脉冲数量。通过定量分析样本脉冲对待检脉冲输出的影响,推导出该干扰方法的理论基础频率唯一性条件,并提出两种应用场景。通过4个仿真实验,分析了普通干扰方法存在的干扰脉冲数量少、控制不灵活等缺陷,验证了本方法对SMI、ADPCA、3DT等STAP的干扰有效性。