双向环形过道布置问题建模及混合鲸鱼算法求解
2021-11-10王沙沙张则强刘俊琦
王沙沙,张则强,刘俊琦,陈 凤
(西南交通大学 机械工程学院轨道交通运维技术与装备四川省重点实验室,四川 成都 610031)
0 引言
在我国制造强国战略的推动下,各行各业积极开展智能制造实践活动。建设智能工厂是实现智能制造的重要手段。设施布局(Facility Layout Problem, FLP)是智能工厂建设的重要环节,对系统的物料处理成本和吞吐量具有重要的影响[1]。因此,FLP在智能制造实现过程中扮演着非常重要的角色。过道布置问题(Corridor Allocation Problem, CAP)[2]作为布局设计的子类,具有搬运效率高的特点,广泛应用于生产生活中;环形布局问题(Loop Layout Problem, LLP)以其相对较低的投资成本和高度物料处理灵活性[3],在制造系统中有广泛应用[4]。双向环形过道布置问题结合了二者的特点,具有重要的实际意义和研究价值。
在过道布置问题(CAP)中,所有设施都排布在过道两侧,起点相同,设施间无间隙,设施间的物料流动必须经过中间过道。根据以往文献,可以将CAP分为单层CAP与多层CAP[5-6]两大类。对单层CAP的研究中,刘思璐等[7]考虑了设施深度对布局的影响;陈凤等[8]考虑了设施摆放方向不同对布局的影响。环形布局问题(LLP)将制造单元沿物料搬运路径布置,从而形成一个封闭环,设施可以位于环路的内部和外部[4,8]或只位于环路外部[9-10],根据不同研究对物料流动的限制不同,分为单向[10]和双向[4]。贾林等[11]提出了环形过道布置问题,假设搬运路径为一个圆环,设施放置在圆环过道两侧,该问题与LLP中设施布置在环路内外两侧的问题具有相似性;王沙沙等[12]通过划分不同路径,对环形过道布置问题进行研究。两篇论文都假设过道的布置起点不可跨越,而在实际生产中,环形过道通常是连通的,设施之间可以进行双向的物料搬运。
目前,求解CAP的方法有精确解法和元启发式方法两种。精确解法主要是数学规划方法,如CHAE等[13]、AMARAL[2]、陈凤等[8]对不同过道布置问题建立了混合整数规划模型。但实际问题中解的空间很大,精确解法需耗费大量时间,因此人们越来越关注有效的元启发式方法。刘思路等[7]采用改进烟花算法求解考虑设施深度的过道布置问题,试验表明改进烟花算法在寻优精度、收敛效率和稳定性方面均有明显优势;王沙沙等[12]采用改进蚁狮算法求解多路径环形过道布置问题,取得较好的求解效果;GUAN等[14]采用花授粉算法求解双层过道布置问题,通过计算不同规模标准算例,验证了花授粉算法求解双层过道布置问题效果优于其他算法;KALITA等[15]采用基于置换的遗传算法求解双目标过道布置问题;毛丽丽等[16]采用改进分散搜索算法求解过道布置问题。上述求解过道布置问题的元启发式算法都是基于2015年及以前的元启发式算法改进而来,而最近几年,出现了一些新的元启发式算法如:黏菌算法(Slime Mould Algorithm, SMA)[17]、蜻蜓算法(Dragonfly Algorithm DA)[18]、鲸鱼算法(Whale Optimization Algorithm, WOA)[19]、蝗虫算法(Grasshopper Optimisation Algorithm, GOA)[20]等。这些算法为解决CAP提供了新的思路和方向。WOA以其结构简单、所需算子少、收敛速度快、勘探开发阶段之间的平衡能力强等优点,在各个工程领域得到了广泛应用。RANA等[21]从2016年~2020年间关于WOA研究的文章中选取82篇进一步研究了WOA在工程各个领域的应用、改进和杂交,研究结果显示,基于WOA的技术被应用于5个领域和17个不同工程领域的子领域,其中61%的工作对算法进行改进,27%的工作将WOA与其他算法混合,12%的工作应用WOA变体解决多目标问题;CHEN[22]通过引入随机备用或随机替换策略和双重自适应权重策略,提出NAWOA(new adaptive whale optimization algorithm) ,提高了基本WOA算法的收敛速度和整体搜索能力。对3个基准函数以及3个工程设计问题进行了综合研究,验证了其性能。实验结果表明,该方法显著改善了基本算法探索性开发性以及收敛模式;HEMASIAN-ETEFAGH等[23]引入新的分组思想,克服了WOA早期收敛问题,在30个标准基准函数上应用Friedman检验的方法,结果显示与其他基准算法相比具有更好的性能;LIU等[24]提出一种基于Lévy飞行和差分进化的混合进化算法来求解车间调度问题,并将其应用于88个车间调度问题基准实例的求解,并与现有算法进行比较,实验结果和统计分析表明,该算法较其他算法性能更优。为解决多目标问题,GOT等[25]提出一种基于Pareto占优的引导种群优化算法(Guided Population Archive Whale Optimization Algorithm, GPAWOA),将拥挤距离纳入基本WOA中,以保持种群多样性,该算法在12个基准函数上进行评估,并应用于4个多目标工程设计问题,实验结果表明算法具有很强的竞争力,能够在收敛性和多样性方面提供Pareto前沿的良好逼近。
鉴于鲸鱼算法求解类似问题具有明显优势,本文提出混合鲸鱼算法,通过嵌入差分进化算法和禁忌搜索的机制,克服鲸鱼算法过早收敛的不足,并采用该算法对双向多路径交互环形过道布置问题进行求解。
1 双向多路径环交互形过道布置问题
1.1 问题描述
双向多路径交互环形过道布置问题可描述为:现有n个设施,排布在环形回路两侧。要求满足以下约束条件:①设施不能重叠,且设施之间无间隙;②环形回路宽度e可变且大于0,宽度由内外设施总长度差确定,且物料沿通道可进行顺逆双向交互;③过道内外两侧设施布置起点相同。
假设条件:①设施之间单位距离的加权物流交互成本固定,为已知量;②设施的物料交互点均位于设施靠过道边线的中点,暂不考虑设施宽度;③设施布置不受场地约束和限制;④不考虑环形过道布置问题中设施与外界的物料交互;⑤为方便计算,将环形回路简化为一个正圆。
双向多路径交互环形过道布置问题示意图如图1所示,图中设施序列为1,2,3,4,5,6,7,将其从3、4中间位置分成两组设施序列,即1,2,3和4,5,6,7,分别计算两组设施的总长度,假设1,2,3序列设施总长较长。图1中将两组设施以粗实线为布置起点,两组设施沿逆时针进行布置;设施之间物料交互经过中间深色通道,假设两设施之间的实际距离为过道宽度与设施靠过道边线中点投影到过道中线上两点之间的弧线长度之和;位于通道同侧设施1和设施3之间路径如两设施之间带箭头组合线所示;位于通道不同侧设施1和设施4之间路径如两设施之间带箭头组合线所示。

1.2 双向多路径交互环形过道布置问题数学模型
数学模型中各个符号参数的定义如表1所示。

表1 数学模型中符号参数定义
在双向多路径交互环形过道布置问题中,过道是一个封闭的圆环,任意两设施之间物料交互有2个方向不同、距离可能不等的可选路径。针对以上特点,以最小化总物料搬运成本为目标,建立双向多路径交互环形过道布置问题的数学模型:
(1)
式(1)为目标函数,计算所有设施间单位距离物流成本cij与实际运输距离dij乘积的最小值。由于设施所放置的位置不同,设施间的实际运输距离计算有差异,位于通道两侧的两个设施之间的物料交需跨越中间通道。因此,
1≤i,j≤n,i≠j。
(2)

θij=min(αij,|αij-2π|),1≤i (3) αij=|θi-θj|,1≤i (4) (5) 1≤i,j≤n;i≠j; (6) (7) 式(3)~式(7)用于确定θij,保证设施之间不发生重叠。通道内外侧边缘对应半径与通道中线对应半径分别为: (8) (9) 计算通道内外侧边缘长度,并令L1作为通道外侧边缘长度 (10) L1≥L2。 (11) 环形布局中,通道宽度的变化会影响物料流动距离,并且在实际生产中通道宽度可以根据生产需要进行设定,本文限制通道宽度大于0。 (12) e>0。 (13) 为保证每个设施都被布置在某个固定位置,对决策变量xik和ykij约束如下: (14) (15) (16) ykij+ykji+1≥xik+xjk,k∈K;1≤i (17) ykij∈{0,1},1≤i,j≤n;i≠j; (18) xik∈{0,1},1≤i≤n;k∈K。 (19) 本文针对双向多路径交互环形过道布置问题的混合整数规划模型确定了每个设施布置在通道内侧或通道外侧进行。文献[12]中只确定设施是否布置在通道同一侧,并没有确定设施具体放置位置,因此在计算放置在不同侧设施投影到过道中线弧长时,采用设施沿直线布置时的距离来近似代替弧长,本文对数学模型进行改进,确定了设施的具体位置,在计算放置在不同侧设施投影到过道中线弧长时更加准确。 鲸鱼算法的灵感来源于座头鲸的起泡网捕食行为。座头鲸喜欢捕食虾群和靠近洋面的小鱼群,在鲸鱼向水面上升时,会制造一个环绕的起泡网。在WOA算法中,目标猎物被认为是最优解,算法步骤描述如下: (1)种群初始化。鲸鱼种群中每个个体由D维度随机向量表示,种群规模用Np表示,公式如下: Xi=xmin+rand(1,D)(xmax-xmin), i=1,2,…,Np。 (20) 式中:xmin和xmax分别为Xi的下界和上界;rand(1,D)表示[0,1]之间的随机数。 (2)包围猎物。座头鲸可以根据猎物的位置来跟踪、包围和捕食猎物。在WOA中,猎物的位置即解空间,当前最佳候选解为目标猎物或接近最优解。在包围猎物阶段,鲸鱼种群向最优解靠近,并更新位置。这个过程表示如下: D=|C·X*(t)-X(t)|; (21) X(t+1)=X*(t)-A·D。 (22) 其中:t为当前迭代次数;X*(t)为当前最优解的位置;X和D为位置向量;A和C为系数向量,随迭代次数改变。每次迭中,当出现更优解时,更新当前最优解X*。 A=2a·r-a; (23) C=2·r。 (24) a从2到0线性递减,r为[0,1]的随机向量。根据式(19),可以将该方法扩展到n维空间,鲸鱼种群将在超立方体中围绕当前最优解移动。 (3)气泡网觅食。座头鲸在觅食时沿圆形或“9”形路径上产生起泡网,两种策略设计如下: 1)收缩包围机制。如式(23)所示,随着迭代进行a线性递减,A取值范围随之递减。更新后鲸鱼种群位置可以在初始位置与当前最优位置之间取得。如图2所示为(X,Y)到当前最优位置(X*,Y*)的搜索空间。 2)位置螺旋更新。 为了模拟座头鲸的螺旋形运动,建立表示座头鲸与猎物之间位置的螺旋方程如下: X(t+1)=D′·ebl·cos(2πl)+X*(t); (25) D′=|X*(t)-X(t)|。 (26) 其中:b定义了对数螺旋的形状,b=1;l为[-1,1]之间的随机数;D′为第i个鲸鱼到猎物(当前最优位置)的距离。 鲸鱼沿着一个收缩圈围绕猎物游动,同时以螺旋形的路径靠近猎物,如图3所示。在[0,1]中选择一个随机数p,有50%的可能性在两种模式之间切换以更新鲸鱼的位置,如下所示: (27) (4)搜索猎物。座头鲸利用A搜索猎物,它们根据彼此的位置随机搜索。步骤(3)和步骤(4)的区别在于,当|A|>1时,鲸鱼的位置依据随机选择的鲸鱼更新,而不是依据当前最佳位置更新: D=|C·Xrand-X|; (28) X(t+1)=Xrand-A·D。 (29) 其中Xrand为当前种群中随机选择的鲸鱼位置。 WOA用于求解连续函数,而不能直接用于环形过道布置问题这种离散问题的求解。因此,本文对随机键编码方式进行处理,将连续问题转化为离散问题,使算法适用于求解环形过道布置问题。鲸鱼的位置不能代表设施排布顺序,但是每个分量大小不同,将分量进行排序,得到设施序列,如图4所示。 2.2.1 与差分进化算法结合提高鲸鱼算法局部搜索能力(HWOA1) 差分进化算法(Differential Evolution algorithm, DE)是一种基于种群差异的进化算法,利用群体内个体之间的合作和竞争产生的群体智能模式来指导优化搜索的进行。基于差分的简单变异操作,使WOA具有较强的全局收敛能力和鲁棒性,非常适合求解一些复杂环境中的优化问题。 WOA通过贪婪选择得到更新后鲸鱼个体位置,这使选择局限于最优解,容易陷入局部最优。当DE嵌入WOA中时,会创建一个包含当前总体和历史最优个体的外部存档集,因此在每次迭代时,大多数新生成的具有DE搜索策略的解决方案都会在外部存档集的指导下更新,这增加了个体之间的信息共享,极大地提高了WOA的局部搜索和开发能力。 差分进化算法原理:从某一随机产生的初始群体开始,通过将种群中任意若干个体之间的向量差加权后按一定的规则比较,产生新个体;如果新个体满足选择条件,则在下一代用新个体取代旧个体,否则旧个体仍保留下来,通过不断迭代计算,保留优良个体,淘汰劣质个体,引导搜索过程项最优解逼近。 标准的DE算法包括变异、交叉和选择操作,具体如下: (1)变异 根据参考文献[24],DE中的变异操作主要有以下8种: 1)“DE/rand/1” Vi,g=Xr1,g+F(Xr2,g-Xr3,g)。 (30) 2)“DE/best/1” Vi,g=Xbest,g+F(Xr2,g-Xr3,g)。 (31) 3)“DE/current/1” Vi,g=Xi,g+F(Xr2,g-Xr3,g)。 (32) 4)“DE/current-to-best/1” Vi,g=Xi,g+F(Xbest,g-Xi,g)+F(Xr1,g-Xr2,g)。 (33) 5)“DE/rand/2” Vi,g=Xr1,g+F(Xr2,g-Xr3,g)+F(Xr4,g-Xr5,g)。 (34) 6)“DE/best/2” Vi,g=Xbest,g+F(Xr1,g-Xr2,g)+ F(Xr3,g-Xr4,g)。 (35) 7)“DE/current-to-rand/1” Vi,g=Xi,g+F(Xr1,g-Xi,g)+F(Xr2,g-Xr3,g)。 (36) 8)“DE/current-to-pbest/1” (37) (2)交叉 在变异完成后将父代个体进行混合,得到一个试验向量Ui=[ui,1,ui,2,…,ui,j,…,ui,D], 其中:j=1,2,…,D;vij,g为个体Vi,g中第j个元素;jrand为[1,D]范围内的一个随机整数,D为变异向量的维数;CR为交叉概率,CR∈[0,1]。 (3)选择 经过变异和交叉操作后,得到一个试验向量Ui,这时通过贪婪选择确定Xi,g+1。当Ui的适应度值大于Xi的适应度值时,Xi,g+1=Ui,g,否则Xi,g+1=Xi,g, (39) 2.2.2 鲸鱼算法与差分进化算法、禁忌搜索算法结合(HWOA2) 禁忌搜索算法的特点是采用禁忌表技术,即用一个禁忌表记录下已经到达过的局部最优点,在新一次搜索中,利用禁忌表中的信息不再或有选择地搜索这些点,以跳出局部最优点。将禁忌搜索与鲸鱼算法结合可以增强算法全局搜索能力,算法流程图如图5所示。 HWOA2伪代码如下: HWOA2 Initialize the whales’ population by Eq... Calculate the fitness of each search agent, X*=the best search agent. while1(c1 while2(t for each search agent Updatea,A,C,Iand p if1(p<0.5) if2(|A|<1) Update the position by Eq. else if2(|A|<1) Update the position by Eq. end if2 else if1(p≥0.5) Update the position by Eq. end if1 if3(flag>1)&&(fit(Xi)>fit(X*)) mutation:mutate by Eq. crossover:cross by Eq. selection:select by Eq. flag=0 end if3 flag=flag+1 end for Check if any search agent goes beyond the search space and amend it. Calculate the fitness of each search agent, update X*. t=t+1 end while2 Initial parameters of TS. if1(t Generate candidate solutions.Calculate function value. if2(fit(Xi) Set the optimal solution with no tabu in candidate solutions as the current solution. else if2(fit(Xi)≥fit(X*)) Set the solution as the optimal solution. Update the tabu table. t=t+1 end if1 c1=c1+1 end while1 return X* 本文所有算例测试试验均是在Window 10操作系统下进行,计算机硬件配置为:Intel(R)Core(TM)i5-9500U,主频3.0 GHz,内存8 GB。计算软件所用版本为:Lingo 11和MATLAB R2016b。本文用到的标准算例S5,S6,S7,S8,S9,S9H,S10,S11,S15来自文献[26],N25-05和N30-05来自文献[27],N40-01来自文献[28],sko42-01和sko49-01来自文献[29]。 为验证了混合整数规划模型的正确性,利用精确求解器Lingo 11对小规模双向多路径交互环形过道布置问题进行求解,计算结果如表2所示。 表2 Lingo求解结果 Lingo对于设施数小于9的测试算例S5~S8均求得最优解,验证了第2章所提混合整数规划模型的正确性。但是在对设施数为9及以上规模算例求解时,Lingo由于自身局限性和问题的复杂程度,对设施数为9的S9问题求到全局最优解需要11 464 s。9~15规模算例已经不能够在较短的时间内进行精确计算,因此对设施数为9及以上的问题记录运行3 600 s时,求得局部最优解。当设施数达到25时,在3 600 s内已无法求出局部最优解。 利用第3章所提混合鲸鱼算法对双向多路径交互环形过道布置问题进行求解,算法参数设置如表3所示。 表3 算法参数设置 为了评估所提混合鲸鱼算法的性能,对比了WOA,HWOA1和HWOA2等3种算法求解不同规模双向多路径交互环形过道布置问题的结果。对不同规模算例进行20次测试试验,结果对比如表4所示,测试的最优计算结果及设施序列详细数据如附表1所示。 表4 WOA,HWOA1,HWOA2计算结果对比表 续表4 分析表4计算结果,HWOA2对不同规模问题求得的最小值均小于WOA和HWOA1两种算法,且求解结果的标准差较小,HWOA2的求解精度明显优于WOA和HWOA1。HWOA1与WOA算法计算结果相比,在设施数为40及以上时,求到的最小值比WOA算法求到的最小值大,但是求解结果的标准差明显比WOA要小,这表明引入差分进化算法增强了WOA求解双向多路径交互环形过道布置题时的局部搜索能力,但随着问题规模的增大,相同参数下HWOA1比WOA更容易陷入局部最优。而禁忌搜索机制的引入,克服了算法陷入局部最优的缺陷,明显改善了算法求解双向多路径交互环形过道布置问题的性能。 根据表4的计算结果,绘制WOA算法、HWOA1算法和HWOA2算法14组测试算例均值对比图,如图6所示。由表4和图6可以看出,HWOA2算法14组算例求解结果均属最优值或近似最优值,其对应的14组均值为119.8,250.2,374.5,599.1,1 086.3,1 835.0,1 176.3,3 078.0,2 949.7,6 974.8,51 896.1,46 719.9,10 176.3,15 832.8。以上数据表明,HWOA2算法在求解双向多路径交互环形过道布置问题时具有良好的求解性能。 根据表4的计算结果,HWOA1算法和HWOA2算法计算结果的标准差与WOA算法计算结果相比较小,因此绘制两种算法计算结果的箱型图,如图7所示。由于不同规模问题计算结果差距较大,为了使箱型图更加直观,绘图时将每次计算得到的数据均除以该组数据的均值。图中横坐标1表示HWOA1算法计算结果的分布情况,2表示HWOA2算法计算结果分布情况。从图7和表4可以看出,HWOA1算法求解各种规模算例结果的标准差为:0.0,9.5,2.3,23.4,6.6,8.3,65.5,48.2,62.1,206.7,1 043.6,1 339.2,153.6,97.6,而HWOA2算法的平均偏差分别为:0.0,0.0,0.0,5.6,0.0,0.0,0.0,16.9,29.7,8.4,122.9,69.9,4.8,11.7,说明HWOA2算法求解更稳定。 为验证算法对于环形过道布置问题法的求解性能,利用HWOA2算法对文献[11]考虑面积成本的双目标环形过道布置问题和文献[12]多路径交互环形过道布置问题中13组算例进行求解,设置相同的求解参数(迭代次数、种群规模等),对不同规模问题进行10次求解,如表5所示。 表5 HWOA2计算文献[11]和文献[12]结果对比表 通过表5可以看出,与文献[11]问题相比:8规模及以下HWOA2算法均可以求得最优值,8规模以上问题HWOA2求得的结果均优于文献[11]最优解,且30规模最优解提升9.60%;与文献[12]中问题对比:9规模及以下HWOA2算法均可以求得最优值,9规模以上问题HWOA2求得的结果优于文献[12]最优解,且40规模最优解提升7.32%。 分析表5可知,HWOA2算法对于单一路径和多路径环形过道布置问题求解均表现出良好的求解效率和质量。 X金属制品厂位于四川省成都市,是一家集设计、开发、制造、销售、为一体的专业门窗生产企业。主要开发生各种钢、铝合金推拉门、防盗门以及其他五金制品。以防盗门为例,其主要生产车间和工艺流程如图8所示。 该企业防盗门种类有44种,包括生态原铜门、仿铜门、电控单元门、复合门等多种类型,企业产品供应四川省多家医院、学校、校区等场所。该企业对市场形势有非常好的认知,生产的新型防盗门使用玻璃夹层,不但起到了良好的防盗作用,并且透光、美观、保温效果好,产品受到广大消费者的青睐。连续几年,企业处于供不应求的状态。 由于该公司生产产品种类较多,制造过程以离散为主,流程为辅。在这种生产情况下,不能采用单一流水线生产,车间区域布置较为混乱。根据课题组2016年对其生产情况的调研发现,该公司生产车间布置缺乏科学理论的指导,导致车间搬运效率较低,生产周期较长。针对该公司生产状况,本章对该企业生产车间布局进行分析和优化。 该生产车间各区域的长度信息以及对应的主要加工设备如表6所示,各区域之间的物流交互量如表7所示。在现存布局情况下,车间的总物流成本为69 157.27 kg·m。 表6 加工区设备信息 由于防盗门的生产周期为20天左右,从顾客预订到上门安装大概一个月左右,因此课题组统计车间加工区一个月的物流量,针对一个标准防盗门的生产工艺流程,所用到的设备是确定的,各设备之间的物流量也是确定的,但是一个月的时间内,加工车间并不是生产单一产品,除了防盗门,还有窗以及其他五金制品。因此,加工区物流量并不是生产单一产品时物流量,不同设备之间存在较大的物料流动。经过统计和整理,该车间加工区物流量如表7所示。 表7 加工区物流量 kg 从表7以看出,在统计中并没有区分每两个区域之间的物流量的方向,如区域1到区域3的物流量为320 kg,从区域3到区域1的物流量也为320 kg。其实,320表示的为区域1和区域3之间总的物流量,不涉及物料流动的方向。 运用所提混合鲸鱼算法对该实例进行求解,算法运行环境与参数设置均与第4章算法参数设置相同。应用闭环布局形式对车间优化后的设施序列为2-9-7-6-4,1-3-5-8-10,优化后物流成本降低到60 124.14 kg·m,较原布局方案减少了13%的成本。然而,由于受到重排成本、加工设备精度要求、电气管道布置、场地大小等因素的限制,车间的实际布局情况较本文提出的双向环形过道布置问题更为复杂,因而本文得出的布局优化方案与实际最优方案还存在一定的差距,仍需进行深入研究,进一步扩展问题模型。 本文提出了双向环形过道布置问题,并建立其混合整数规划模型,通过精确求解器Lingo对小规模问题求精确解,验证了混合整数规划模型的正确性。针对所提问题,提出了混合鲸鱼算法,在WOA中引入差分进化和禁忌搜索策略来求解大规模双向环形过道布置问题,加入差分进化操作提高了WOA的局部搜索能力,禁忌搜索机制增强了算法的全局搜索能力。为了评价混合鲸鱼算法,首先用该算法求解了14个不同规模算例,并与文中2个算法进行比较;其次,用该算法分别求解环形过道布置问题和多路径交互环形过道布置问题,并与参考文献中的结果进行对比。两个试验结果验证了所提算法的性能优于对比算法。最后将混合鲸鱼算法应用到实际问题中,为车间布局提出了改善建议。 当前研究主要集中在单层与静态环形过道布置问题,后续将针对更符合实际生产的多层及动态环形设施布局问题进行深入分析和解读。2 混合鲸鱼算法
2.1 经典鲸鱼算法介绍


2.2 混合鲸鱼算法介绍


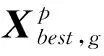

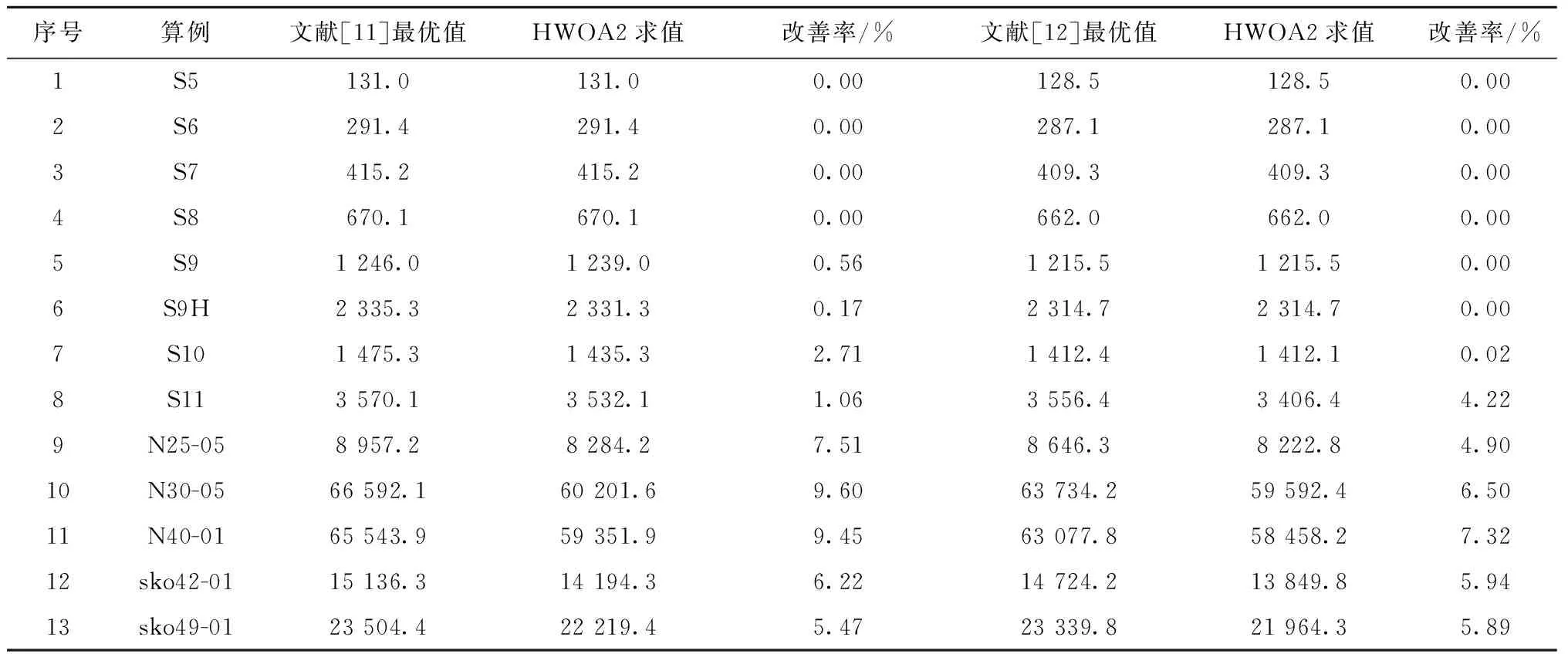
3 计算结果及分析



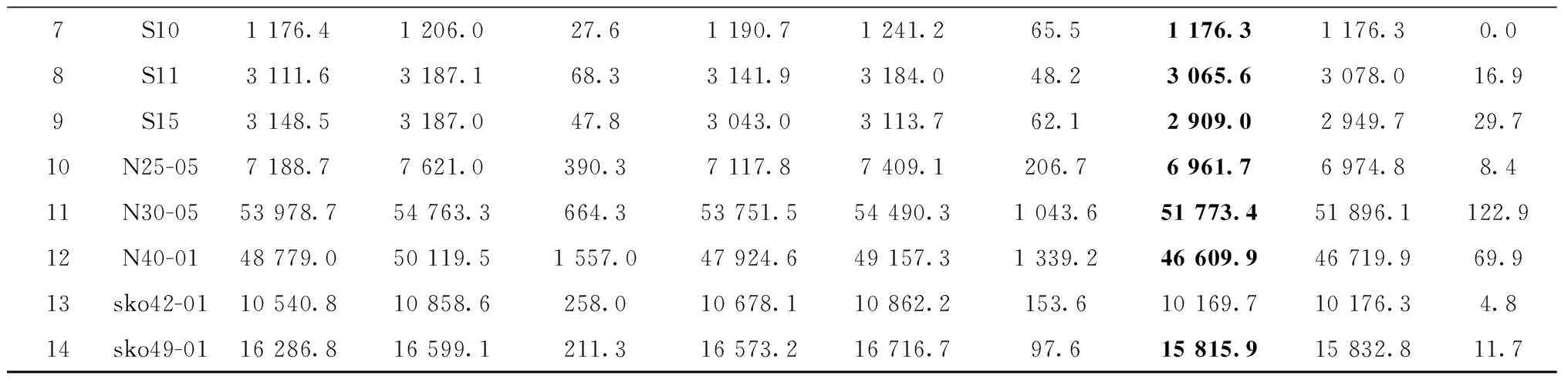


4 实例应用



5 结束语
