两阶齐套性约束的制造系统排队网建模与缓冲区优化

张惠煜，陈庆新，毛 宁，李 翔,2+，俞爱林，梁祖红

(1.广东工业大学 广东省计算机集成制造重点实验室，广东 广州 510006；2.湘南学院 电子信息与电气工程学院，湖南 郴州 423000)

0 引言

定制化装备制造企业生产过程中，随着市场对定制化产品的要求越来越高，针对密封要求特别高的精密偶件、传动精度特别高的运动副，在现有互换技术标准无法满足小间隙配合的设计要求时，需要采用研配的方法进行精细加工，以取得所需的配合关系(紧配合、动配合、过渡配合等)，例如轮胎模具生产中的侧板和活字块加工。侧板和活字块都需要先后经过粗加工单元、车弧面加工单元和精加工单元的加工，其中车弧面加工单元中，每块侧板需要与活字块装配起来配合加工，然后拆解并分别进行精加工作业，最后再进行装配加工。

定制型制造系统的生产过程中存在众多不确定因素，如订单到达时间、工序加工工时、工艺路线变化等。随机环境下，如何在制造系统中优化配置有限的制造资源(设备、缓冲区容量等)，降低企业投资成本，同时提高车间生产能力、缩短生产提前期、提高订单准时交货率，是制造企业建立智能工厂时迫切需要解决的问题。定制型企业的一个显著特征就是具有订单交货期约束，因此生产周期是制造系统规划设计的关键性能指标。实际生产过程中，在制品(Work-In-Process, WIP)的排队等待时间往往远大于其加工时间，合理地设置缓冲区的容量可以减少在制品的排队队列长度及其等待时间，缩短生产周期，提高准时交货率。缓冲区配置问题(Buffer Allocation Problem, BAP)是基于现有的车间资源，研究各个缓冲区最大容量的配置方案以获得最优的系统性能或投资方案。缓冲区容量设置得太低会降低系统的生产效率，设置得太高则无法起到调控系统生产周期的作用。

由于目标函数以及约束条件通常为非线性函数，BAP是一类非线性整数规划问题。随着系统规模的扩大，每个缓冲区容量组合构成的解空间规模也会随着扩大而导致维数灾问题，BAP也是一类NP难组合优化问题[1-2]，而且系统性能指标是关于决策变量的非封闭函数，因此无法采用传统非线性规划中基于梯度的搜索算法求解此类BAP。目前，国外已有一些针对BAP研究的综述文献，例如GERSHWIN等[3]，DEMIR等[4]，HUDSON等[5]以及WEISS等[6]，但这些文献都只是针对串联结构的流水车间系统。BAP可以分为3类：①初始优化问题,在满足系统产能需求的约束下，最小化缓冲区总容量;②双重优化问题,在最大化系统产能的同时最小化缓冲区总容量;③组合优化问题,以最小化缓冲区总容量为目标，同时考虑其他指标作为约束指标或优化变量，如平均在制品数，平均生产周期等。常用的求解方法是由一种生成方法(Generative Method)和一种估算方法(Evaluative Method)通过迭代的方式进行求解：生成方法主要包括枚举法、动态规划法、搜索法(如梯度搜索算法、启发式算法、智能算法)等;估算方法主要包括解析法和仿真法。基于排队理论(queuing theory)[7]的解析法是针对随机系统性能估算的有效工具，精确解法虽然可以获得精确解，但存在状态空间维数灾问题。对于复杂结构的系统，一般采用近似解法或仿真法。仿真法虽然可以获得逼近精确的解，但是需要进行多次重复独立实验，耗时很长，会极大地增加资源配置优化问题求解算法的时间复杂度。近似解法的算法运行时间则非常短，这在优化系统资源配置时将会很大程度地提高求解效率。基于排队网(queuing network)[8]模型计算系统性能指标值并应用于求解BAP，相关研究主要有文献[1-2]，文献[9-11]等。国内也有少数学者研究制造系统的BAP，如张良安等[12]研究了一种机器人自动化生产线缓冲区容量分配问题的优化方法，采用连续型生产线模型，以生产线最大可用度为优化目标，设计遗传算法得到缓冲区容量分配的次优解;李翔等[13]针对多级流水车间缓冲区容量优化设置问题，建立连续时间马尔可夫链的排队网模型计算系统的关键性能指标，以任务拒绝率为约束条件，提出一种缓冲区容量优化的启发式优化算法。

优化系统资源配置时，需要解决的首要问题是如何快速、精确地计算出系统的性能指标值(如产出率、在制品数、生产周期等)，这是判断一个资源配置方案是否满足预期要求的依据。然而，由于系统的性能指标无法由决策变量描述为一个具有具体的、封闭表达式的函数，从而导致难以采用现有随机规划模型的求解方法。因此，求解这类随机规划模型需要高效的求解方法，以快速获取精确的系统性能指标值，在优化求解过程中判断决策变量是否满足约束条件。排队网络模型作为一种系统建模分析的数学工具，是将一个或一组制造资源作为节点，节点上任务的堆积作为队列，节点之间的关联关系作为连边，从而将整个生产系统描述为一个由若干节点耦合的网络。进而通过网络节点的变化、节点连边的变化及节点连边间的相互作用对该模型进行研究，分析和计算系统性能指标值。与无限容量缓冲区的排队网模型相比，由于可能发生的阻塞(blocking)现象使得系统一般不存在乘积形式解(product-form solutions)，因此有限缓冲区开排队网模型(open queuing network with finite buffer)的求解难度更大。现有的求解方法中，精确解法(exact solution method)[14]可以求解稳态的精确解，但存在状态空间的维数灾问题；状态空间分解法(decomposition of state space method)[15]可以获得较为精确的近似解，但会随着系统规模增大而提高算法时间复杂度，并且只适用于具有负指数分布的Markov模型；广义扩展法(generalized expansion method)[16]可以求解一般分布的排队网模型，但只适用于具有串联、分流和合流结构的前馈式排队网模型。

本文研究对象为具有研配工序的制造系统，针对装配系统的性能评估模型比一般拓扑结构的系统模型更加困难，因为装配过程具有齐套性约束，即需要等待不同类别的工件都到达，且加工设备可用的情况下才能进行装配作业，因此为节点之间带来了强相关性。装配结构，包括拆解结构的系统模型称为装配/拆解(Assembly/Disassembly，A/D)网络。现有文献的求解方法主要是由针对一般简单结构网络模型的方法拓展而来，其中大多数采用GERSHWIN等[17-18]提出的“两站子系统”分解的分析方法，研究了一类有限缓冲区、不可靠服务和负指数分布的模型;MANITZ[19-20]应用了该方法并将其进行拓展，研究具有一般分布服务时间的装配/拆解网络。但是，该方法适用于不考虑外部到达的“饱和”模型，不能用于求解本文所研究的系统模型。目前，国内学者对于装配系统的建模分析都是将其简化为常规工作站，并没有考虑装配过程的同步约束，如孟凡力等[21]，张平等[22]。据笔者的文献调研，尚未见相关研究报道针对具有双重同步约束和固定配对约束且一般任意分布的排队网模型的研究成果。

本文研究了具有研配工序的制造系统排队网建模与缓冲区优化方法，与前人研究相比的创新之处体现在：

(1)研究对象为具有研配工序的制造系统，目前并未有针对该类具有多阶齐套性约束的排队网模型的研究报道。

(2)优化模型具有产出率和生产周期双重约束，现有文献的BAP模型几乎都只考虑产出率约束，因为具有多重约束问题构成的解空间可能是非凸的，而使得问题难以求解。生产周期是定制型制造系统规划设计的关键性能指标，即便生产系统具有充足的产能，若生产周期无法满足订单交货期要求，也不符合系统规划设计需求，则需要在BAP中权衡产出率约束和生产周期约束。

为此，本文针对具有研配工序的制造系统，建立了两阶齐套性约束的有限缓冲区开排队网模型，针对3种不同假设的模型提出拓展的广义扩展法，求解系统性能指标值，并将其嵌入Polyblock算法，优化系统缓冲区容量配置。

1 问题描述

1.1 两阶齐套性约束的排队网模型

该排队网模型如图1所示，其中方框表示缓冲区(排队队列)，圆框表示自动化加工设备(服务台)，两者组合表示工作站(节点)。系统加工过程分为4个阶段：

(1)两个不同类型的工件a和b，分别到达系统并在加工阶段Ⅰ中f个串联的常规工作站上依次进行加工；

(2)到达研配工作站Y进行配对，并在同一台设备上进行研配加工；

(3)完工后，两个工件拆解分离，分别到达加工阶段Ⅲ中r个串联的常规工作站上依次进行加工，此时同类工件之间不再具备互换性；

(4)最后，到达总装工作站Z完成装配作业后离开系统。

不同于传统的装配/拆解系统(A/D system)，这类具有研配工序系统的显著特点是：

(1)两阶齐套性约束：两类工件分别经过研配阶段和总装阶段进行加工时均需要具备齐套性约束；

(2)研配节点的双重同步约束：两类工件的配对输入过程以及拆解输出过程均具有同步约束(synchronisation constraint)；

(3)总装节点的固定配对约束：进行总装的两个工件必须是在研配阶段进行配对加工的。

系统模型假设如下：

(1)系统外工件到达过程(exter-arrival process)服从泊松分布；

(2)每个工作站的加工过程(processing process)以及工作站之间的工件到达间隔过程(inter-arrival process)的分布类型的假设如表1所示，其中假设1模型和假设2模型均为假设3模型的特例。

表1 系统模型假设

1.2 BAP优化问题数学模型

优化模型如下，决策变量为系统缓冲区容量配置向量，即X={xi}，

(1)

s.t.

Θ{X}≥Θmin，

(2)

T{X}≤Tmax，

(3)

X∈N+。

(4)

其中式(1)为优化目标，即求解最优的缓冲区配置向量Xopt从而最小化总缓冲区容量Z。同时，满足式(2)的产出率约束，即平均产出率不小于Θmin，以及式(3)的生产周期约束，即平均生产周期不大于Tmax。由于Θ{X}和T{X}为非封闭的函数，因此需要根据排队网模型求解获得。

2 系统性能指标估算方法

2.1 研配节点与总装节点的分解

如图2所示，将研配节点分解为两个虚拟的子服务台Mi和Mj，加工速率均为μY，同时分别与对应的缓冲区BaY和BbY组成两个具有研配耦合关联的子节点i和j。两类工件a和b在研配节点的“配对—加工—拆解”过程，可以转化为其分别在两个子节点上同时进行相同的处理过程。因此，只要满足同步输入约束，就能满足同步输出约束。同理，将总装节点也进行分解。由于系统服务规则为“先到先服务(First in First Out, FIFO)”，由研配节点输出的两类工件a和b在分别经过加工阶段Ⅲ的后到达总装节点的次序不变。由此，将问题转化为处理同步到达的等待问题。

2.2 拓展的广义扩展法(GEM′)

基于广义扩展法，本文只介绍用于处理研配节点和总装节点的改进方法，对于常规节点详见文献[16]。

2.2.1 网络重构

针对假设3的GI/G/1/K节点模型，如图3所示。在研配节点的在子节点i和j前分别添加一个排队模型为GI/G/∞的虚拟节点hi和hj，用于容纳因目的节点满而被阻塞的工件。同理将系统每个节点进行扩展，从而将整个系统网络重构为一个Jackson网[17]。

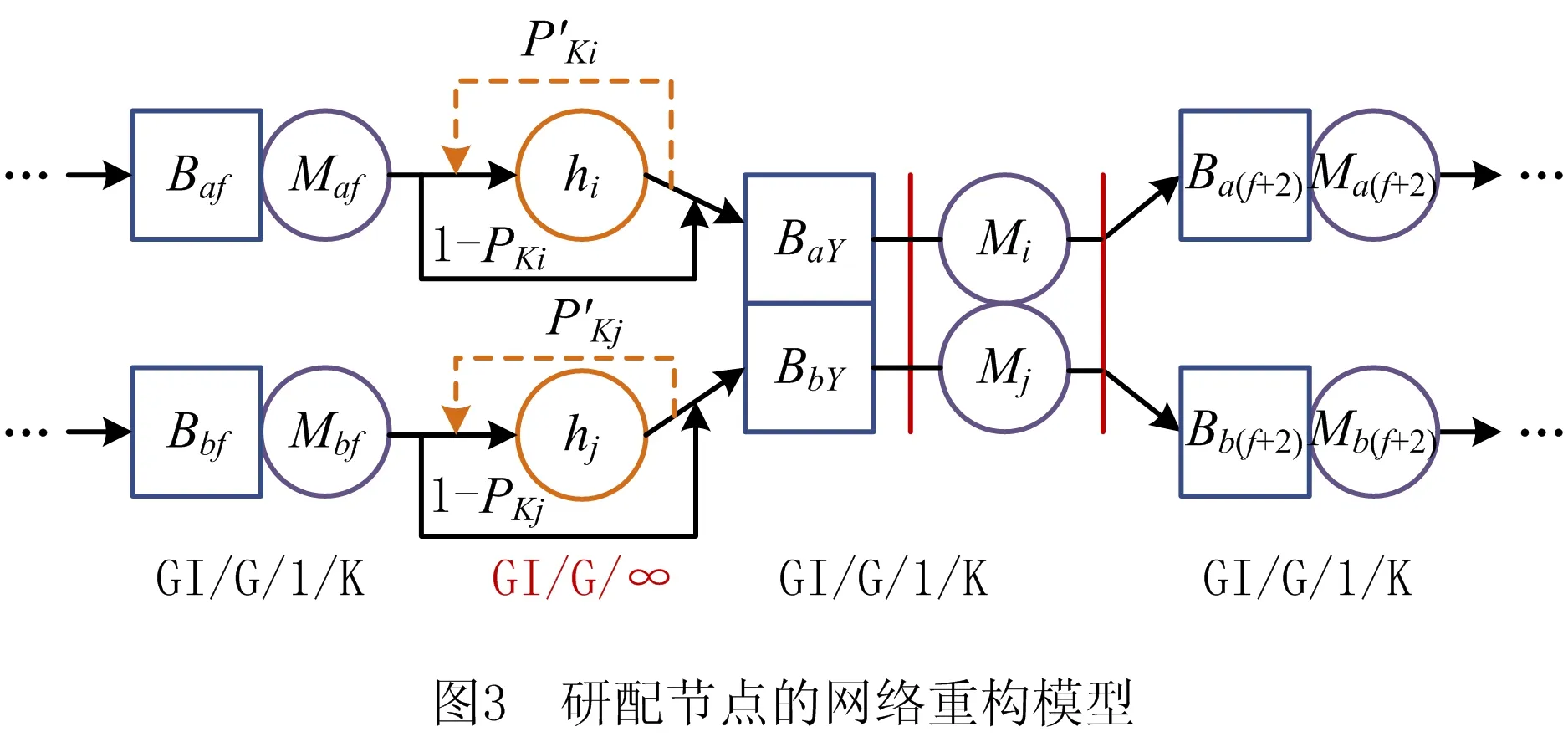
2.2.2 参数估算

由于子节点i和j是同等的，以子节点i为例，参数计算过程如下：

(1)基于扩散近似原则[23]，节点i的阻塞概率近似计算公式为：

(5)

(2)虚拟节点hi的回返阻塞概率为：

(6)

(3)基于更新理论，在节点i上被阻塞工件的延迟时间与节点i上加工件的剩余加工时间具有相同的分布。因此，虚拟节点hi的平均加工速率为：

(7)

(4)由于输入到节点i的工件来自被阻塞的工件流和不被阻塞的工件流两者之一，因此节点i输入过程分布的平方变异系数(SCV)为：

(8)

(5)由虚拟节点扩展的系统为Jackson网模型，因此，节点i输出过程分布的SCV为：

(9)

式中Lqi为节点i中平均排队队长，且

(10)

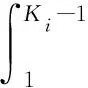
(11)

2.2.3 参数修正

稳态条件下，节点的输入和输出速率平衡，因此节点i的输出速率为：

(1-PKi)ρi，

(12)

式中ρh=λh/μh。同理，可以计算节点j的输出速率Θj。

因此，考虑研配节点的输入过程和输出过程的同步约束，其输入速率为：

ΛY=min{ΘY(i-1),ΘY(j-1)}，

(13)

输入过程分布的SCV分别为：

(14)

(15)

输出速率为：

ΘY=min{ΘYi,ΘYj}，

(16)

输出过程分布的SCV为：

(17)

考虑研配节点输入过程同步约束的等待问题，即当两个缓冲区其中一个为空一个不为空时，不为空的缓冲区中工件需要等待，导致排队队长增加。因此，修正节点的排队队长分别为：

(18)

(19)

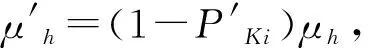
2.2.4 指标计算

根据工件流方向，逐个节点依据上述方程组迭代求解，并计算相关的参数值传递到后续节点，直至总装节点，从而获得整个系统的性能指标值：

Θ=min{ΘZi,ΘZj}，

(20)

(21)

2.3 算例分析

本节设计两个实验算例，分别研究输入过程分布类型的假设以及缓冲区容量对系统性能的影响，同时与仿真实验对比验证算法的精确性。采用MATLAB软件编写解析算法程序，并在Siemens Tecnomatix PlantSimulation(eM-Plant)软件上建立离散事件仿真模型。

2.3.1 加工时间为负指数分布的模型算例

为分析假设1和假设2对应不同到达间隔时间分布类型的影响，同时分析研配节点和总装节点的瓶颈效应，考虑3组算例，如表2所示。表中：(A0)为初始方案;(A1)同时增加两个节点的缓冲区容量;(A2)同时提高两个节点的加工速率;(A3)同时提高研配和总装节点加工速率，并增加其他节点的缓冲区容量。算例求解结果如表3所示，其中“Δ1/%”和“Δ2/%”分别为假设1和假设2模型应用广义扩展法求解结果与仿真结果的相对偏差百分比。

表2 指数分布加工时间模型算例参数

由表3可以看出，与仿真结果对比，应用拓展的广义扩展法求解假设1模型的系统平均产出率偏差较小，而系统平均生产周期的偏差则非常大。对于假设2模型，虽然拓展的广义扩展法求解的系统平均产出率的偏差比假设1模型的结果略大，但是对于系统平均生产周期的相对偏差则要小得多。这是因为，假设1模型中节点到达间隔时间分布为负指数分布，即节点输入过程具有Markov性，但是对于存在到达同步约束的研配节点和总装节点，则不一定仍具有Markov性。由此可见，将到达间隔时间分布假设为一般任意分布更符合实际生产情形。

表3 指数分布加工时间模型算例结果

续表3

如图4所示为各组算例系统性能指标的变化曲线，算例(A1)同时增加研配和总装节点的缓冲区容量，系统平均产出率有所提高，然而系统生产周期也随之延长。算例(A2)同时提高两个节点的加工速率，系统性能均略有改善，但这有可能使得瓶颈漂移至其他节点。算例(A3)为较低加工速率的节点设置较大容量的缓冲区，系统产出率明显提高，然而系统生产周期也增加。

2.3.2 加工时间为一般分布的模型算例

针对假设3模型，考虑一个包含14个工作站的系统模型，其中加工阶段I和加工阶段Ⅲ的节点数均为3。设置4组算例方案：①初始方案;②增加节点缓冲区容量;③降低系统负荷率，即降低系统外工件到达率;④增加节点缓冲区容量，同时降低系统负荷率。分别考虑3类加工时间分布：二阶爱尔朗分布、负指数分布、二阶超指数分布，对应的加工过程平方变异系数(Squared Coefficient of Variation, SCV)为：(B1)0.5，(B2)1.0，(B3)1.5。算例求解结果如表4所示，其中“Δ/%”为应用广义扩展法求解结果与仿真结果的相对偏差百分比。可以看出，由拓展的广义扩展法求解的系统平均产出率和生产周期，与仿真结果的相对偏差都较小。

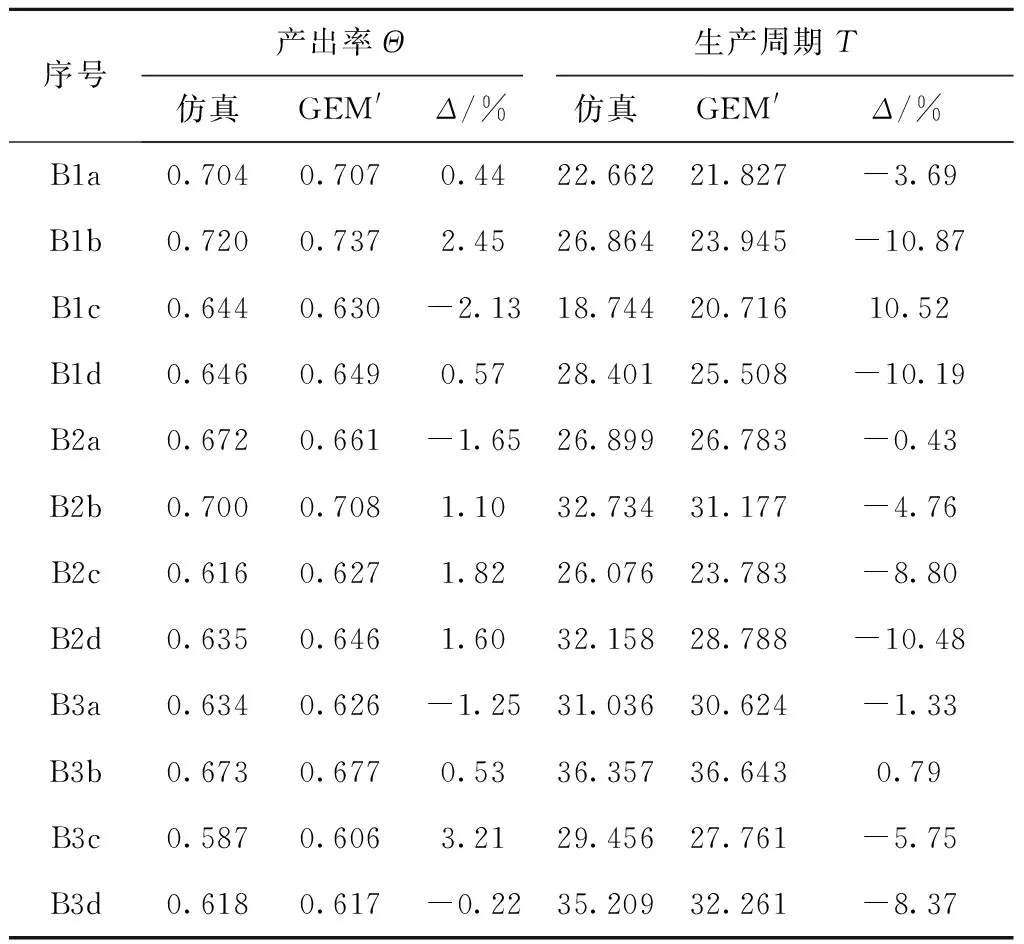
表4 一般任意分布加工时间模型算例结果

如图5所示为各组算例系统性能指标的变化曲线，解析结果与仿真结果具有相同的渐近趋势。加工时间SCV用于描述加工时间分布的离散程度，SCV值越大，离散程度越大。因此，随着SCV值增大，系统平均产出率降低、生产周期增加。方案②增加系统节点的缓冲区容量，虽然可以降低节点的阻塞概率而提高系统平均产出率，但会增加系统平均在制品的数量，因此增长系统平均生产周期。方案③降低了节点的工件流强度，而使得系统性能降低，即系统平均产出率降低，生产周期增长。方案④对系统产出率的影响趋于方案③，而对系统生产周期的影响则趋于方案②。

综上可知，缓冲区容量的变化对于系统生产周期的影响大于对系统产出率的影响，若要权衡同时考虑系统产出率和生产周期而改善系统性能，需要合理地优化配置系统的缓冲区容量。

3 缓冲区容量配置优化方法

3.1 求解算法

由第2.3节的算例实验结果可以看出，系统性能约束指标与决策变量之间存在偏序单调性，即随着缓冲区容量的增加，系统平均产出率和生产周期单调增长。因此，BAP是一个单调整数规划模型，可以采用离散Polyblock算法[24]获得更精确的结果。算法原理是基于外逼近法的思路，通过一个已知顶点的多胞形不断逼近可行域，使得问题的解逼近于原凹极小问题的解。

如引言所述，由于性能约束指标是关于决策变量的非封闭函数，将拓展的广义扩展法嵌入Polyblock算法中，在每个迭代过程中判断决策变量是否满足约束条件，求解思路如图6所示。由于本文优化模型具有两个性能指标约束，将两个约束分别获得的两个可行域的交叠区域作为联合可行域进行搜索。算法详细步骤如下：

步骤1初始化。

步骤2区域分割。

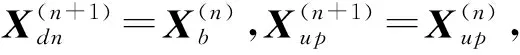
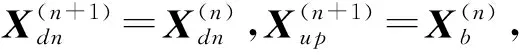
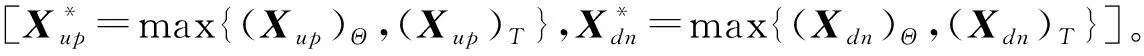
步骤3枚举搜索。

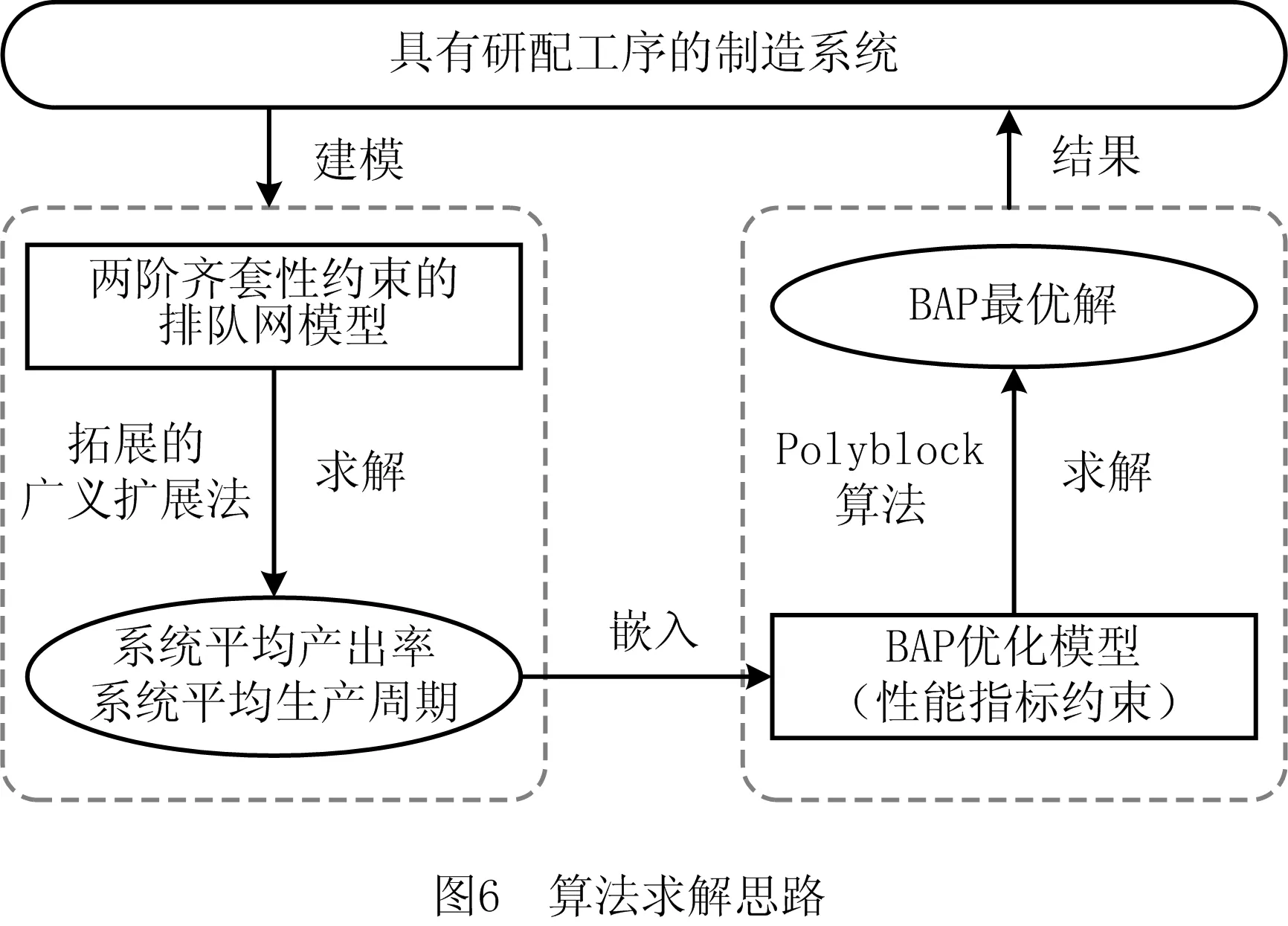
3.2 优化案例

以某轮胎模具机加工车间的侧板和活字块加工为例，侧板a和活字块b的任务投放率(工件到达率)分别为λa=1.4(个/h)和λb=1.5(个/h)，每个工作站的加工速率为μi=1.8(个/h)。针对不同规模的生产系统，即系统具有不同数量的工作站，优化结果如表5所示，其中X1和X2分别为应用本文提出的嵌入广义扩展法的Polyblock算法和嵌入广义扩展法的粒子群算法获得的最优解。可以看出，对于较小规模的系统，两种方法获得的最优解一致，而对于较大规模的系统，嵌入广义扩展法的Polyblock算法能够获得更好的解。对于确定性问题，Polyblock算法能够获得精确的全局最优解，然而嵌入的排队网建模分析方法为近似计算方法，因此获得的解为近似的最优解，而对于进化算法存在易陷入局部最优的问题。此外，由拓展的广义扩展法计算的系统产出率和生产周期的近似度都较好。可以看出，本文所提出的方法可以有效求解具有研配工序的制造系统资源配置优化问题，在满足车间产能和订单交货期的条件下，优化缓冲区容量配置，降低投资成本。

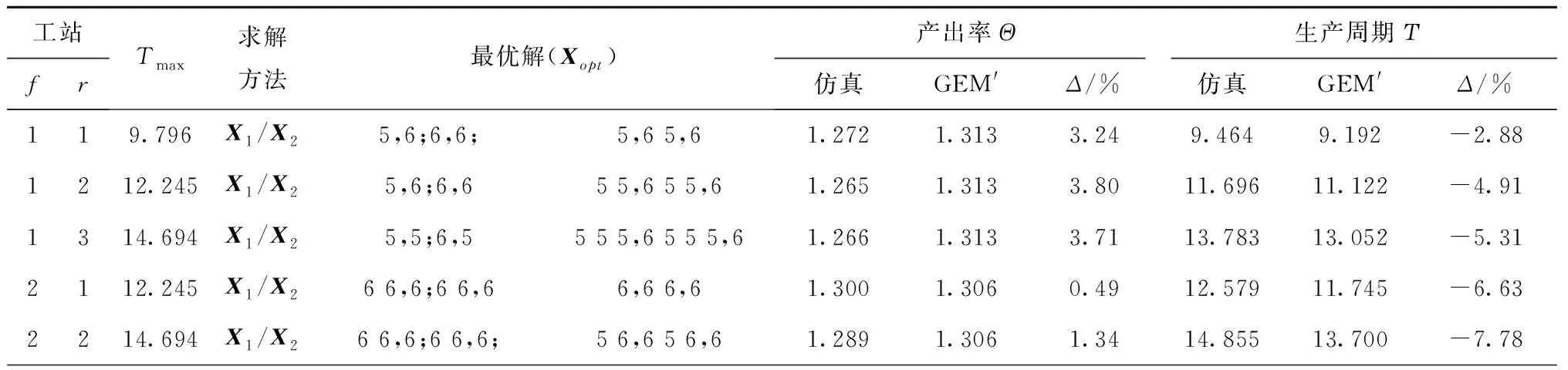
表5 具有研配工序的制造系统缓冲区优化配置

续表5

4 结束语

针对定制型装备制造企业，考虑具有研配工序的生产系统，建立两阶齐套性约束的有限缓冲区开排队网模型。针对研配节点的双重同步约束和总装节点的固定配对约束，基于3类不同分布类型的假设模型，提出拓展的广义扩展法，近似求解系统性能指标值。算例实验表明，基于Markov性假设的系统模型虽然可以获得较好的系统平均产出率，但是系统平均生产周期则非常差；基于一般任意分布假设的模型获得的系统性能指标值均具有较高的近似度。此外，对于系统缓冲区容量，对系统生产周期的影响大于其对系统产出率的影响。最后，针对缓冲区容量配置优化问题，建立随机非线性整数规划模型，提出嵌入拓展广义扩展法的Polyblock算法，并通过优化案例求解制造系统缓冲区容量的配置方案。

本研究只针对具有两阶齐套性约束的制造系统，实际生产中还存在多阶段齐套性约束的加工过程。基于本文研究成果，未来将研究具有多阶齐套性约束的制造系统排队网建模和资源配置优化方法。