基于VB的陀螺定向测量方位角计算设计与实现

郭庆坤，王忠，来彦明，魏辉，朱君

(济南市勘察测绘研究院，山东 济南 250101)

1 引 言

当前，计算机技术飞速发展，为测量工作和数据计算带来了极大的便利，通过计算机编程，把测量工作方法或数据处理方法程序化，使计算机按照测量人员的思路进行工作，大大提高了测量数据计算的效率，降低了人工计算的出错概率[1]。陀螺定向测量方位角的计算通常采用人工计算，计算过程烦琐、困难，效率较低，且容易出现计算错误，利用Visual Basic程序语言设计编写的算法，可有效解决上述弊端，快速准确地计算出子午线收敛角、仪器常数、坐标方位角等待求量。

2 陀螺定向测量方位角计算方法

经过地面任意一点均存在坐标北方向、真北方向、陀螺北方向三个基本方向，坐标北方向为坐标系X轴所指的方向，真北方向为过地球表面某点的真子午线的切线方向，陀螺北方向为陀螺仪敏感地球角动量而实际测得的北方向[2]。由真北方向起算的方位角为真方位角，用A表示，由坐标北方向起算的方位角为坐标方位角，用α表示[3]，由陀螺北方向起算的方位角为陀螺方位角。坐标北方向与真北方向之间的夹角为子午线收敛角，用γ表示[4]，陀螺北方向与真北方向之间的夹角为陀螺仪的仪器常数，用△表示[5]。陀螺定向测量原理关系图如图1所示。

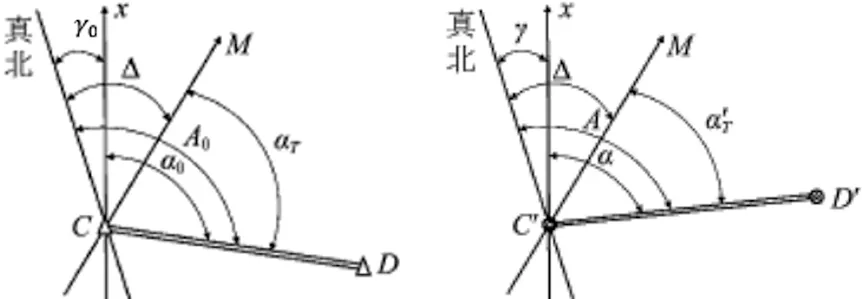
图1 陀螺定向测量原理关系图

在高斯投影下的坐标系中，任一方向的真北方位角与坐标方位角存在以下关系：

A=α+γ=△+αT

(1)

在地上已知点C架设仪器，根据地上已知测站点坐标方位角α0、子午线收敛角γ0和测得的地上已知边陀螺方位角αT，利用式(1)，求得仪器常数：

△=α0+γ0-αT

(2)

(3)

3 程序界面设计与实现

3.1 界面设计

根据地下定向边陀螺方位角测量“地面已知边-地下待定边-地面已知边”的测量程序[6]，地上已知边和地下待定边分别有多次测量成果，相同测线的多次测量成果在原始记录手簿中即可计算出互差和平均值，为使用户界面输入尽量少的数据，故界面中只设计了地上陀螺方位角平均值和地下陀螺方位角平均值的输入文本框。

本着用户界面设计简洁清晰，无须多媒体效果的原则，根据地下待定边坐标方位角计算所需要的数据，用户界面主要包含了地上数据输入、地下数据输入、数据计算成果三个部分，整个界面使用了VB 6.0的Frame控件、Label控件、Text控件、Command控件和Statusbar控件进行设计，可以直观明了地显示输入数据和计算成果数据，同时可以看到数据计算的实时时间。数据输入完成，点击“计算”按钮即可进行数据计算，点击“退出”按钮即可退出程序。用户界面如图2所示。

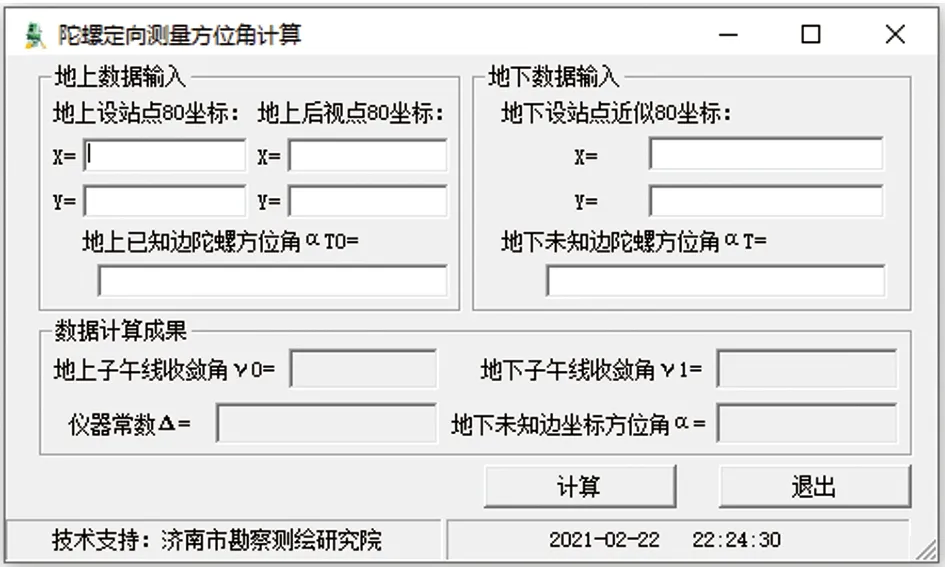
图2 用户界面

3.2 程序流程与实现

代码的设计应简捷有效，并能保证有效运行，经反复调试的代码应尽量简化，增加代码的可维护性和可读性。程序流程如图3所示。

图3 程序流程图

根据计算的程序流程，首先判断输入数据是否为空或有非数值型数据，满足要求后，通过定义的Function[7]过程，把输入的度分秒转化为小数度，然后计算地上、地下设站点子午线收敛角、地上坐标方位角，最后计算仪器常数和地下待定边坐标方位角。

(1)判断输入数据是否为空或有非数值型数据

为防止输入数据有遗漏或输入数据中有非数值型数据，特设计此判断过程，在判断输入数据是否有遗漏时，利用if text1.text=””语句进行判断，利用msgbox函数进行信息提示；判断是否有非数值型数据时，利用isnumeric函数进行判断，利用msgbox函数进行信息提示，具体代码此处不再展示。

(2)度分秒转化为小数度

因输入的陀螺方位角为度分秒模式，如83.35083表示83°35′08.3″，为方便计算，需要将度分秒转化为小数度，故定义了度分秒转化小数度的Function过程，主要代码如下：

Private Function xsd(jd As Single) As Single ′度分秒转换成小数度

Dim d As Integer，f As Single，m As Single

d=Int(jd)

f=Int((jd-d) * 100) / 60

m=(jd * 100-Int(jd * 100)) * 100 / 3600

xsd=d+f+m

End Function

此过程将输入的度分秒转化为便于计算的小数度，如89.35083表示的89°35′8.3″，转化为89.58564度。

(3)计算地上坐标方位角

根据地上已知点的平面坐标，计算已知边坐标方位角，定义了计算坐标方位角的Function过程，主要代码如下：

Private Function zbfwj(x1 As Double，y1 As Double，x2 As Double，y2 As Double) As Double ′根据坐标计算坐标方位角

Dim dx As Single，dy As Double，a As Single

Const PI As Single=3.14159265357

dx=x2-x1：dy=y2-y1

a=Atn(Abs(dy) / Abs(dx)) * 180 / PI

If dy>0 And dx>0 Then

zbfwj=a

ElseIfdy>0 And dx<0 Then

zbfwj=180-a

ElseIfdy<0 And dx>0 Then

zbfwj=360-a

ElseIfdy<0 And dx<0 Then

zbfwj=180+a

End If

End Function

(4)计算子午线收敛角

子午线收敛角的计算有两种方法，一种是通过经纬度计算，计算公式为：

γ=sinB*△L[8]

式中B为设站点纬度，△L为设站点经度与中央子午线经度之差。

另一种是通过子午线收敛角系数k值表计算，计算公式为：

γ=ky[9]

式中，k为系数，根据设站点纵坐标X由表查出，y是该点的横坐标，γ的单位为分。

本设计采用的是k值表计算法，定义了子午线收敛角计算的Function过程，此过程代码较长，此处只体现部分代码如下：

Private Function zwxslj(ByVal x1 As Double，ByVal y1 As Double) As Double ′根据K值法计算子午线收敛角

Dim K As Double，x2 As Double，x3 As Double，y2 As Double

x2=Int(Left(x1，4) / 100) * 100

x3=(x1-(x2 * 1000)) / 1000

y2=y1 / 1000

Select Case x2

Case 100

K=0.0085+0.0085 * x3 / 100

Case 200

K=0.017+0.0085 * x3 / 100

……

Case 6000

K=0.7437+0.0248 * x3 / 100

End Select

zwxslj=(K * (y2-500)) / 60

End Function

通过以上几步过程，可以求得地上已知边的坐标方位角、地上设站点的子午线收敛角、地下设站点的子午线收敛角，从而求得仪器常数，最终求得地下待定边的坐标方位角，并在用户界面中显示。

4 程序功能验证

本文以济南市轨道交通R2线一期工程和R3线一期工程共7条定向边的陀螺定向测量数据为例进行程序的分析验证。济南市轨道交通R2线全长 36.4 km，其中地下线 34.8 km、高架线 1.6 km，共设置19座车站，其中地下站18座、高架站1座，大致呈东西走向；济南市轨道交通R3线全长 21.57 km，共设置车站13座，全部为地下站，大致呈南北走向。在R2线选取了4个区间的4条定向边，在R3线选取了3个区间的3条定向边，共7条定向边的陀螺定向测量数据，通过人工Excel计算和程序计算结果的对比，对程序的可行性和准确性进行验证，人工Excel计算过程中，子午线收敛角的计算采用经纬度的方法，利用公式γ=sinB*△L计算。程序计算与Excel计算成果对比如表1所示。

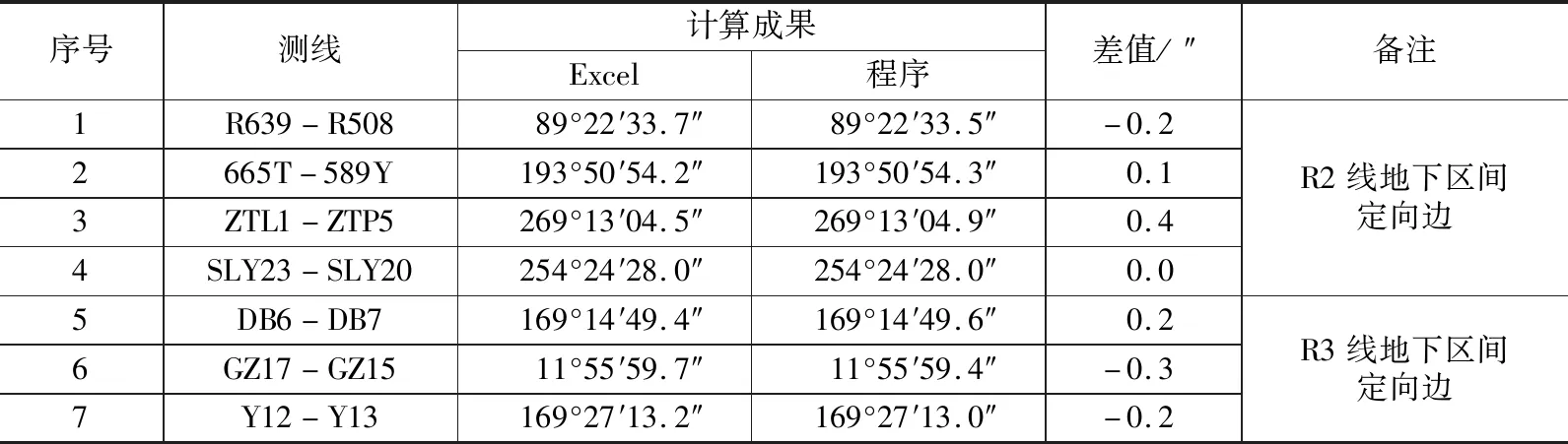
程序计算与Excel计算成果差值表 表1

通过表1中Excel计算与程序计算成果的对比分析，得用程序计算的地下待定边的坐标方位角与人工用Excel计算的坐标方位角之差均在±0.5″以内。经过分析，程序计算与Excel计算成果的差值，为用经纬度计算子午线收敛角和用k值表计算子午线收敛角两种不同计算方法所致，这也验证了程序中所定义的子午线收敛角计算Function过程的正确性。可认为程序计算的地下待定边的坐标方位角与Excel计算的坐标方位角是一致的，所计算的成果是可靠的，可用于对隧道内导线边方位角进行校核，以提高贯通精度。

5 结 语

本文根据陀螺定向测量方位角计算的方法，使用Visual Basic语言对陀螺定向测量方位角计算程序进行了设计与实现，并通过济南市轨道交通R2线和R3线共7个区间的7条陀螺定向边实际测量数据，验证了程序的计算成果可靠。通过程序的应用，可以有效地提高陀螺定向测量方位角计算的效率，降低人工计算的出错概率，可为地下隧道测量相关从业者提供借鉴和参考。