汽车驾驶机器人的自适应执行器故障补偿控制设计
2021-11-10姚雪莲丁东东葛婉君吴鸣宇
姚雪莲, 丁东东, 杨 艺, 葛婉君, 吴鸣宇
(江苏理工学院 汽车与交通工程学院, 江苏 常州 213001)
随着计算机技术、网络技术、微机电系统(micro-electro-mechanical system,MEMS)等高新技术的发展,机器人被广泛应用于制造业、医疗服务、教育娱乐、勘探勘测、生物工程以及救灾救援等众多领域.为了提高机器人的智能性和精度,现代机器人中装有许多的传感器和执行器,然而一旦单个或多个执行器发生故障,就可能导致控制律不能被完整地执行,进而影响系统的控制性能,导致整体任务失败,甚至影响整个系统的稳定性,因此,需要对机器人进行有效的容错控制设计.许多国内外学者对执行器故障补偿问题进行了深入研究并提出了一系列行之有效的方法.文献[1]针对多机械臂系统的卡死、失效以及偏差类型的执行器故障提出一种协同容错控制方法,基于状态观测器对不可测量状态和未知故障进行估计,结合重构方法构建容错控制器,通过估计的状态信息和故障参数对控制器参数进行更新.文献[2-3]综合考虑机器人机械臂的干扰、未知参数和执行器多重不确定问题,提出基于终端滑模控制的鲁棒容错控制方法,能够有效解决突变的执行器故障问题.文献[4]将多模型切换控制方法应用于机器人的容错控制中,获得期望的控制效果.文献[5-6]分别基于拉格朗日方法和动态平面控制设计容错控制策略,文献[5]在不需要明确失效下限的前提条件下,有效解决空间机器人的失效故障.文献[7]针对过驱动的机器人,利用分层滑模控制方法设计容错控制器用于解决未知的偏差故障问题.文献[8]将滑模控制和Backstepping控制相结合,所设计的容错控制方法可解决机器人的故障、参数和扰动的综合不确定问题,并与其他容错控制策略进行比较,体现了其算法的优越性.
在众多类型的机器人中,汽车驾驶机器人是一类能够代替驾驶员进行起步、加速、制动等操作的机器人,可以多次反复使用,且无需对车辆进行改装,被广泛用于汽车自动驾驶试验中.驾驶机器人由换挡机械手、油门机械腿、制动机械腿和离合机械腿构成,通过各种驱动方式,使机器人的操作能够具有人肌肉的快速性和柔顺性.东南大学、南京理工大学和南京汽车研究所共同研制各种驱动结构的汽车驾驶机器人,如直线电动机、可伸缩的和电气混合式结构的机器人,并针对各种结构的驾驶机器人分别采用模糊控制[9]、神经网络[10]、滑模控制[11]、分层协调控制[12]等方法实现车辆的速度跟踪控制任务.文献[13]针对绳索绞车的汽车驾驶机器人的位置跟踪问题提出一种基于二阶滑模跟踪控制算法.与其他类型的机器人一样,汽车驾驶机器人的执行器故障给系统的性能带来不确定的影响,也需要结合先进的控制方法解决汽车驾驶机器人实际运行过程中可能发生的不确定故障问题,保证汽车行驶系统的稳定性、安全性和可靠性.因此,笔者针对研究汽车驾驶机器人运行过程中可能遭受的(时间、参数和模式等)多重不确定执行器故障,将Backstepping和自适应控制相结合,通过Backstepping设计基础控制律保证机器人系统的稳定性.构建参数化的综合控制器结构,将故障参数融合到控制器参数设计中,采用自适应方法对其进行估计,保证不确定执行器故障情况下闭环系统的稳定和跟踪给定指令.
1 模型的建立
1.1 机械腿动力学模型
汽车驾驶机器人机械腿分为制动/离合/油门机械腿,其机械腿的原理和动力学模型相似.汽车驾驶机器人的机械腿主要由驱动器和机械部分构成.机械腿二维模型如图1所示.机械腿包括壳体、驱动器、导轨、滑块、大腿、小腿和踏夹板等,其中驱动器作为汽车驾驶机器人的执行器之一,可以是气缸驱动、电动机驱动或者气缸和电动机混合驱动.

图1 机械腿二维模型
汽车驾驶机器人机械腿结构简图[14]如图2所示,该结构是摇杆结构,驱动器1推动滑块,滑块带动驱动器2驱使大腿转动.而且驱动器2能独立地驱动使大腿转动,从而保证无论哪个驱动器发生故障,都能够通过设计合适的控制律保证机械腿正常转动.

图2 机械腿结构简图
建立图2所示的直角坐标系,杆1绕O点的转动惯量为
(1)
式中:m1为杆1的质量;l1为O点到A点的距离.
根据平行轴定理,杆2相对O点的转动惯量JO2可由式(2)求得,即
(2)
式中:JC为杆2绕质心C点的转动惯量;m2为杆2的质量;lOC为C点到O点的距离;l2为A点到B点的距离;α3为杆1与杆2的夹角,α3为定值.
总转动惯量为
J=JO1+JO2.
(3)
总动能为
(4)
式中:α1为杆1与x轴的夹角.
以x轴所在平面为零势能作为参考面,总势能Ep可由式(5)求得,即
(5)
式中:Ep1和Ep2分别为杆1和杆2的势能;α1为杆1与x轴的夹角;α2为杆2与水平线的夹角.
将式(1)-(5)代入拉格朗日方程Lr=Ek-Ep,Lr为拉格朗日函数,可得汽车驾驶机器人所需的驱动力矩为
(6)
式中:M1和M2分别为驱动器1、2产生的转矩.
(7)
由式(6)可得
(8)
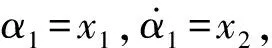
(9)

u=[u1,u2]T=[M1,M2]T.
1.2 执行器故障模型
汽车驾驶机器人的驱动器可能发生的卡死、失效、时变偏差故障表示为
(10)

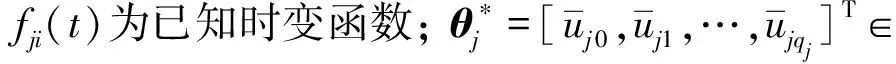

fjqj(t)]T∈Rqj+1为已知基函数;tj为故障发生时刻.
定义σ(t)=diag[σ1(t),σ2(t)]为执行器故障模式矩阵,当第j个执行器发生故障时σj(t)=1,否则σj(t)=0.所以,当系统发生不确定故障时,系统输入可表示为
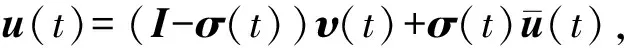
(11)
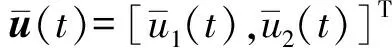
2 执行器故障补偿设计
将Backstepping控制与自适应控制相结合,提出一种自适应执行器故障补偿控制设计方法.
2.1 Backstepping控制设计
定义系统的跟踪误差为
e1=x1-αd1,
(12)
式中:αd1为期望轨迹指令.
对式(12)求导得
(13)
定义虚拟控制量为
(14)
式中:k1>0.
定义e2=x2-e2d,对其求导得
(15)
定义Lyapunov函数为
(16)
求导得
(17)
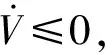
(18)
式中:ω为驱动信号;ωd为理想反馈控制信号;k2>0.
2.2 执行器故障补偿器的设计
首先对无故障、u1故障(M1故障)和u2故障(M2故障)3种情况分别设计控制器,然后通过加权融合方法设计综合控制器.
2.2.1控制器的设计
(19)
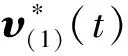
将式(19)代入式(18)得
(20)
选取h代入式(19)可得
(21)
式中:k11=(g(x)h)-1.
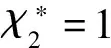
令
(22)
将式(22)代入式(18)得
(23)

求解得
(24)
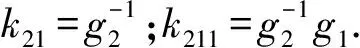

令

(25)
将式(25)代入式(18)得
(26)
求解得
(27)

(28)
当故障信息(故障参数、故障模式和故障发生时间)未知时,需要设计自适应控制器,即
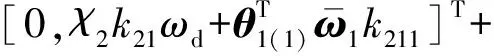
(29)

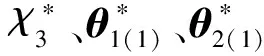
式(15)改写成反馈控制信号误差方程为
(30)
根据式(28)、(29)可得
(31)
设计参数的自适应律[15]为
(32)
式中:γ11>0;γ12>0;γ2>0;γ3>0;fχ11、fχ12、fχ2、
fχ3、fθ1(1)、fθ2(1)为投影算子,保证参数有界;Γ1>0;Γ2>0.
2.2.2性能分析
无执行器故障时,Lyapunov函数为
(33)
u1故障时,Lyapunov函数为
(34)
u2故障时,Lyapunov函数为
(35)
将式(13)、(30)和(32)代入式(33)-(35),求导后可得
(36)
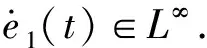
综上所述,基于Backstepping设计的自适应故障补偿器所得的反馈控制规律式(30)和自适应律式(32)可以使非线性系统在不确定执行器故障u1或u2时,保证闭环系统的稳定性和渐近跟踪性能.
3 仿真验证
基于自适应融合算法设计容错控制器,并将其用于解决汽车驾驶机器人运行过程中可能发生的不确定执行器故障问题,保证运行过程中闭环系统稳定和渐近输出跟踪.为了验证所设计方法的有效性,采用Matlab软件进行仿真分析.
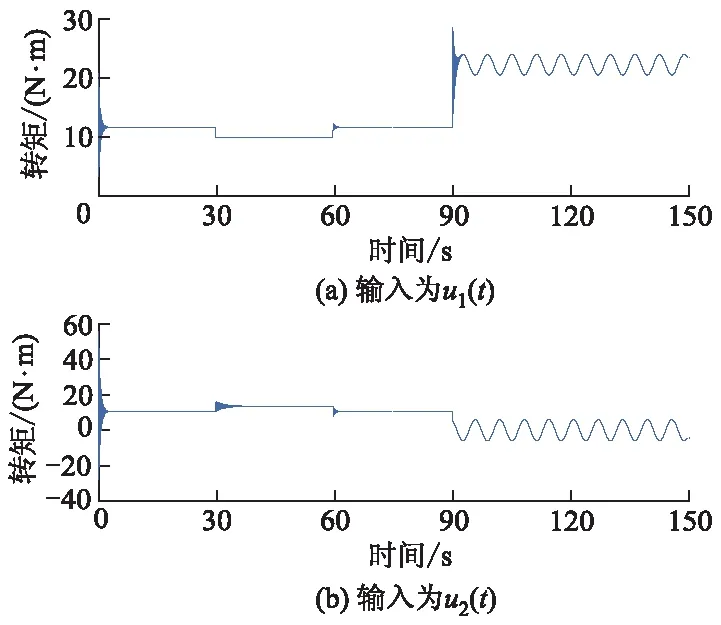
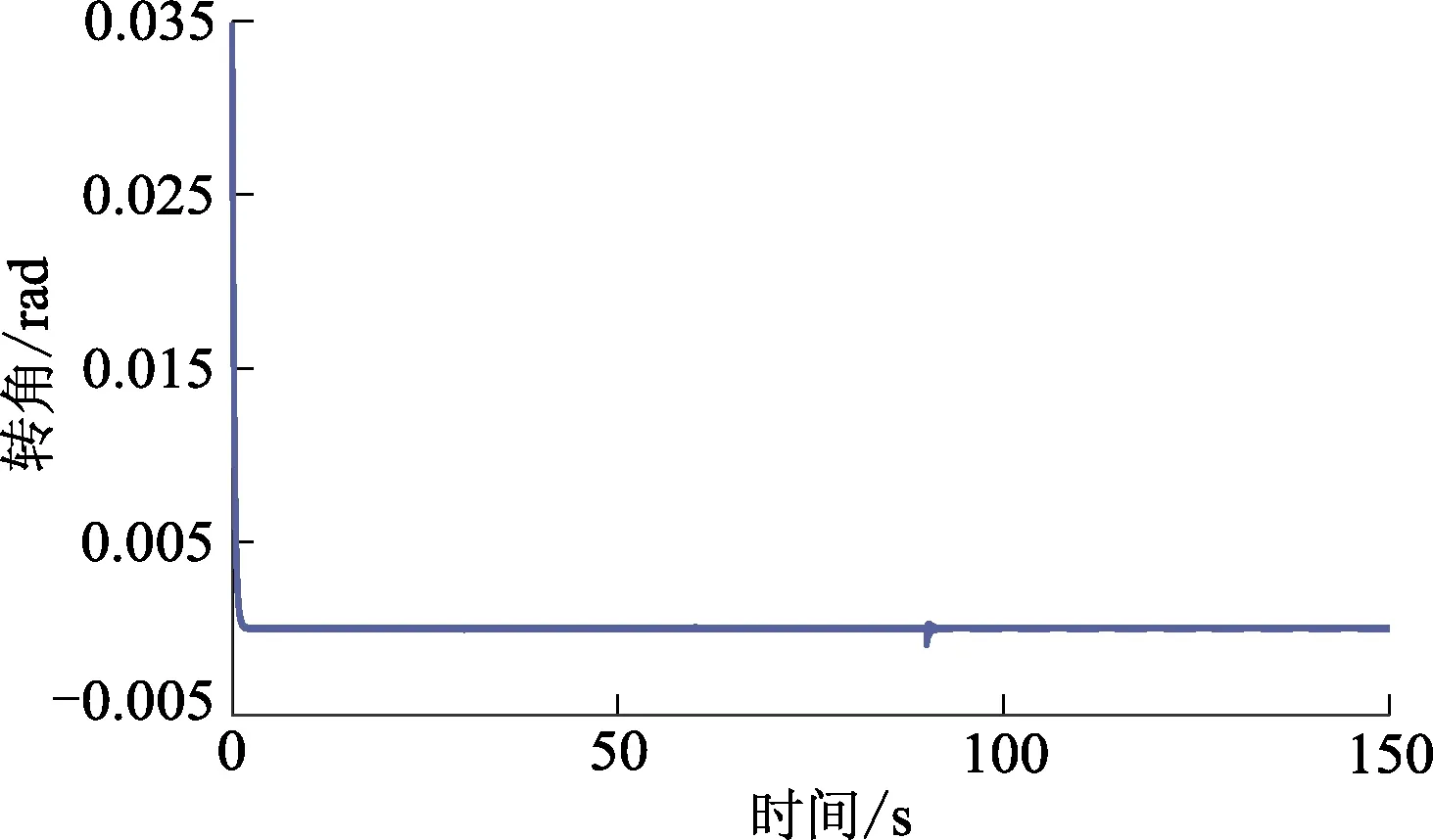
故障条件如下: 当0 χ12(0)=1,χ2=χ3=0,θ1(1)(0)=θ2(1)(0)=[0, 系统控制输入信号如图3所示,系统输出与参考信号如图4所示. 图3 系统控制输入信号 从图4可以看出:未进行故障补偿时,系统在执行器发生常值故障和时变故障时,出现较大偏差;当进行故障补偿后,系统无论是在无故障条件下还是执行器发生不确定故障条件下,所设计的控制器都能保证系统的稳定性和渐近输出跟踪;在t=30 s和t=90 s时执行器发生故障,系统的输出指令在跟踪指定指令过程中出现偏差,如图5所示. 图5 系统的输出跟踪误差 从图5可以看出,随着时间的延长,偏差逐渐减小,从而验证此控制方法的鲁棒性,仿真结果也表明基于Backstepping的自适应故障补偿器的有效性。 针对汽车驾驶机器人机械腿驱动器可能发生的不确定故障,提出一种基于Backstepping的自适应故障补偿的方法.自适应故障补偿器的关键在于不知道故障信息(故障时间、故障的模式和故障值)的情况下,分别针对各故障情况设计控制器,然后通过自适应算法对故障参数和故障模式进行估计,结合加权算法构造一个综合的自适应故障补偿器.当机器人执行器在发生不确定故障时,还能保证闭环系统的期望性能.仿真结果表明此方法是有效的.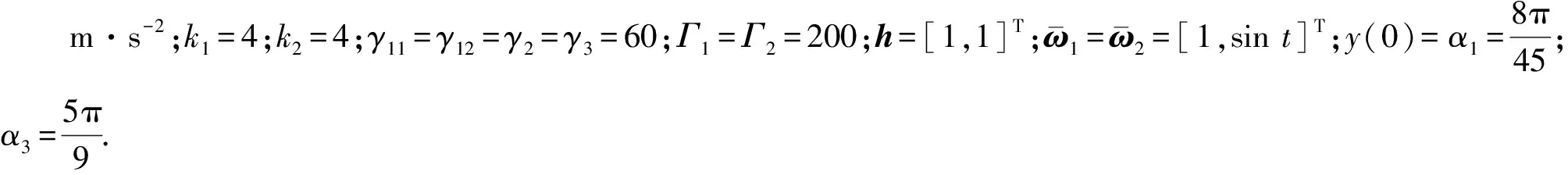

4 结 论
