基于马尔科夫优化的移动边缘计算车载网络任务卸载

李沁颖，曹青松

(江西科技学院 a. 信息工程学院，b. 智能工程学院，江西南昌 330098)

车载网络利用车辆与车辆(vehicle to vehicle，V2V)[1]、车辆与基础设备(vehicle to infrastructure，V2I)[2]、车辆与互联网(vehicle to network，V2N)[3]等方式进行无线通信，以保证车辆驾驶的安全性和提高交通通行的效率，实现路况预测和协同驾驶；但是集中式车载网络受到通信距离的限制，不能高效地利用网络资源，并且传输与计算也无法满足移动设备用户需求，因此移动边缘计算(mobile edge computing，MEC)车载网络引起广泛关注。将MEC引入车载网络，令车载数据下沉至网络边缘和本地设备[4-5]，协助车载系统迅速分析决策[6]，极大地节省了网络资源的容量，同时也提高了车辆的服务质量(quality of service,QoS)。此外，考虑车辆用户对实时通信的需求和车辆计算资源能力有限[7]，MEC车载网络将分布密集的计算任务资源部分或全部分配至网络边缘进行计算卸载[8]，以降低计算成本，改善计算性能，缓解数据传输过程的丢包、延迟问题。Zhang等[9]考虑MEC车载网络中车辆移动性，采用契约理论设计了最优计算卸载策略的资源分配方案，结果表明，MEC车载网络能够有效提高车辆任务的计算效率。为了提高任务计算结果的可靠性，Zhang等[10]利用MEC服务器接收车载节点任务信息，以预测车载节点可通信区域，从而提出目标服务器的计算卸载方案。Huang等[11]针对网络频繁切换带来的负担问题，将蜂窝网络中的车辆通信业务卸载到车载网络中的V2V通信路径，为车辆数据传输提供了新方案。Chen等[12]研究多用户无线卸载问题，利用分布式博弈理论，设计基于移动边缘云计算的任务卸载方法，综合考虑了多信道无线通信环境。Al-Shuwaili等[13]采用凸近似定理，提出将通信和计算资源分配至MEC服务器，以解决资源分配造成的能量消耗过大的问题。Zhang等[14]提出多弧度结合机制，利用该机制模型匹配MEC服务器和移动终端，使得计算任务能够卸载至最优MEC服务器，降低了任务卸载过程中产生的开销。

已有的基于MEC车载网络资源分配和任务卸载的文献大多考虑单一的智能网联汽车，将车辆计算任务完全卸载至移动边缘设备或本地车辆； 而在实际驾驶环境中，智能网联汽车多以车队的形式进行驾驶，目前鲜有对智能网联式车队选择最优任务卸载方案的研究。本文中针对MEC车载网络，建立移动车辆参考点群组移动模型，利用簇头车辆节点预估群组其他车辆的移动速度和方向，构建任务卸载模型，将计算任务分别卸载至相邻的车辆节点和MEC服务器，采用马尔科夫优化过程，获取车辆节点状态，通过状态转移，选择资源分配和任务卸载联合优化方案，从而实现提高任务卸载效率的目标。

1 MEC车载网络系统模型

根据任务需求将资源按不同比例分配至MEC服务器和相邻车载网络车辆，建立MEC车载网络系统模型，进行任务卸载计算，其中系统模型主要包含车载网络车辆移动模型和任务卸载模型。

1.1 车载网络车辆移动模型

考虑模型中的车辆移动方向，采用参考点群组移动模型作为车辆移动模型，如图1所示。

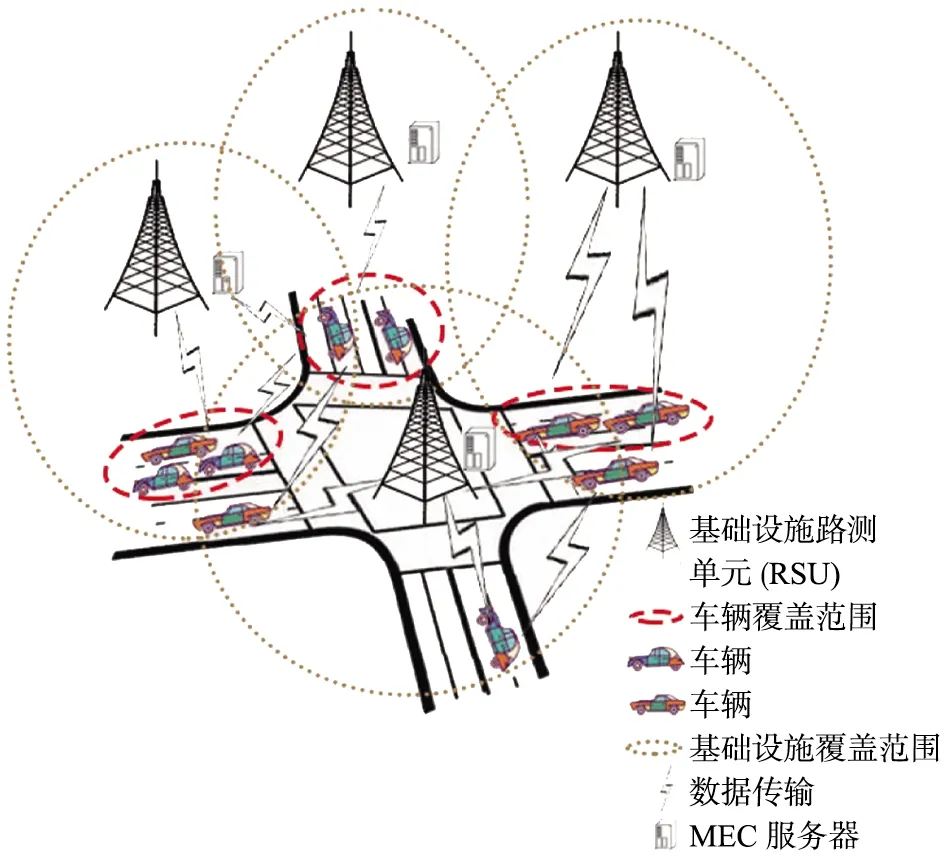
图1 基于移动边缘计算(MEC)的车载网络场景

对于模型中的车辆移动方向，仅考虑5种移动情况，即正北N、正南S、正东E、正西W、静止状态F，记为a={N, S, E, W, F}。

EVGm=Ecen+random()Rsas，

(1)

DVGm=Dcen+random()Raaa，

(2)

式中： random()为取随机量的函数；Rs、Ra分别为车辆速度偏移率、车辆角度偏移率；as、aa分别为车辆速度偏移量、车辆角度偏移量。

1.2 任务卸载模型

T—任务计算总过程； TMEC—移动边缘计算(MEC)服务器任务计算总过程； Tv—车辆任务计算总过程； Tt—任务传输过程；任务传输至MEC的过程；任务传输至本地车辆的过程； Tw—任务在MEC服务器的等待过程；任务在MEC的执行过程；任务在本地车辆的执行过程。图2 智能网联车队车辆任务计算过程

假定当前群组Gm车辆节点VGm发布计算任务VWGm=(λWVGm, (1-λ)WVGm)，其中λ为计算任务划分至本地车辆的比例，λWVGm为传输至本地车辆节点的计算任务容量，(1-λ)WVGm为通过无线通信链路传输至MEC服务器的计算任务容量。执行结束后需将计算结果返还至车辆节点，如果在MEC服务器任务计算结果返还过程中，车辆节点计算任务还未结束，则需要等待执行。

为了更好地利用闲置网络资源，达到最大任务时间最小化的目标，令执行时间等于任务传输时间，计算恰当的资源分配和任务卸载比例。任务资源分配为

(3)

(4)

其中资源分配和任务卸载比例为

(5)

式中：φ为计算任务的复杂度；β为任务传输完整度；Cv为车辆计算数据能力，即单位时间内车辆中央处理器(CPU)循环执行的周期数；Sv为车辆网络通信传输速度。

当前车辆节点处于行驶状态时，可将任务卸载至当前节点可用的通信范围内具有相同行驶方向和相似行驶速度的相邻车辆和MEC服务器；当前车辆节点处于静止停泊状态时，可将任务卸载至车辆节点可用通信范围内的其他停泊邻居车辆和MEC服务器，如图3所示。

VGm={V1, V2, , Vb}—智能网联式车队车辆节点，m=1, 2,,x，x为群组个数，b为群组车辆节点个数； WVGm—车辆 节点的计算任务容量； λ—计算任务划分至本地车辆的 比例； 1-λ—计算任务划分至MEC服务器的比例。图3 移动边缘计算(MEC)车载网络任务资源分配模型

1.3 任务卸载计算

当计算任务分配至本地相邻车辆时，车辆节点计算任务执行时间为

(6)

车辆计算任务按需求比例分配至计算数据能力为CMEC、计算任务复杂度为φ的MEC服务器，则MEC服务器执行任务时间为

(7)

在计算过程前后，需要通过无线通信链路将任务传输至计算节点，则计算任务传输至MEC服务器和相邻车辆的传输时间分别为

(8)

(9)

式中：SMEC为MEC服务器网络通信传输速度。

由此，计算任务在MEC服务器、本地相邻车辆的执行时间和传输时间分别为

(10)

(11)

(12)

T=max{TMEC,Tv,Tt}

。

(13)

根据式(13)获得的计算任务执行总时长，对所有资源分配和任务卸载方案进行最优决策。

2 马尔科夫优化过程

MEC车载网络下资源分配和任务卸载的马尔科夫优化过程表示为(A，S，P，R)，其中A为行为空间，S为系统状态空间，P为状态转换概率，R为开销收益。

2.1 行为空间

在时间段[1,k]可选择的数据传输路径为行为空间A={a1,a2, ,ak}，其中

(14)

式中γ为当前数据通过多种状态的邻居车辆节点传输。

2.2 状态空间

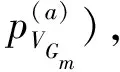
(15)

2.3 状态转移

状态转移pz(i,j)为在时间段[k-1,k]，当前行为从当前选择的路径i转移至路径j的条件概率，即

(16)

其中

1.2.2 研究过程 征得源量表作者同意后对N-QOL量表进行汉化。首先由2名英语较好的研究生将量表翻译成中文，其中1名托福考试成绩优异；然后由研究者和以上2人共同对翻译结果进行综合整理，再请2名大学英语教师将量表回译成英文，与源量表进行比较，最后经过4名翻译人员及研究者的反复商讨确定初步版本。将汉化后的量表提交给5名相关专家，采用4分法对量表内容效度进行评价，1=不相关，2=有点相关，3=相关，4=高度相关。根据专家意见对量表进行修改后进行预试验，选取20例夜尿症患者填写量表，了解患者对各条目的反应，必要时进行文化调试。最后将量表应用于较大样本的夜尿症人群中，评价汉化后量表的性能。

(17)

选择不同运动方向的pγ0,γ1(i,j)的计算过程如下。

1)当γ0≠F且γ1≠F时，

(18)

其中

(19)

式中：psuc为当前车辆节点传输数据至邻居车辆节点的成功概率；H为传输路径的传输容量。

2) 当γ0=F时，

(20)

1)当ak=0时，计算任务选择在本地相邻车辆中传输，则任务卸载至当前车辆节点或其他邻居车辆节点，即

(21)

2)当ak=1时，计算任务选择在无线通信中传输，则任务卸载至MEC服务器节点，则

(22)

3)当ak=γ时，计算任务选择在车辆行驶方向传输，则任务分别卸载至相邻车辆节点和MEC服务器节点，即

(23)

2.4 系统最优决策

在基于MEC车载网络的系统模型中，车辆可利用马尔科夫优化过程选择最优决策方案，并将任务卸载至本地相邻车辆和MEC服务器节点，从而获得任务最短执行时间，因此系统在整个任务执行周期的期望执行时间ttot为

(24)

式中：arg min{·}为取任务执行时间最小值函数；η为折扣因子，0≤η≤1；t为时间周期；TGm为车辆群组任务执行最短时间。

通过式(24)可获得最短执行时间，从而选择资源分配和任务卸载的联合优化方案。

3 基于马尔科夫优化的任务卸载流程

3.1 系统初始化

在车辆行驶区域中，将所有车辆节点、RSU设备节点、MEC服务器节点进行自定义组织，构建MEC车载网络。由于系统网络结构是相对稳定的，并且每个系统节点均有对应的计算能力、传输速度、当前状态等参数信息，因此当网络结构中节点状态发生变化时，系统网络结构也会进行重新构造，每个节点参数信息随之更新。

3.2 任务卸载流程

假设发布计算任务的车辆节点为初始节点，并考虑当前车辆节点可通信范围内的所有相邻车辆节点和MEC服务器节点的参数信息，形成计算任务的所有资源分配和卸载方案。同时，根据任务复杂度、完整度及任务量，计算车辆任务分配至本地车辆节点和MEC服务器的比例。

将可通信范围内的所有车辆节点设为备选节点，根据车辆状态信息计算出每个备选节点的任务传输成功率，即为预选节点跳转成功率，从而组成状态转移矩阵。

通过状态转移矩阵可以采集到计算任务的所有预选传输路径，计算每个传输路径中任务卸载的总时长，从而确定任务卸载最优方案，即任务卸载时长最短的传输路径。

4 仿真实验

4.1 仿真实验参数

设计相应的仿真实验，并通过MATLAB软件实现，具体仿真实验参数如表1、2所示。

表1 智能网联式车队车辆仿真环境参数

表2 移动边缘计算(MEC)车载网络任务卸载仿真实验参数

4.2 仿真结果分析

从不同任务量、时间段2个方面进行考虑，分别比较车辆计算任务全部卸载至车辆节点、MEC服务器及分别卸载至车辆节点、MEC服务器的总时长，结果如图4所示。

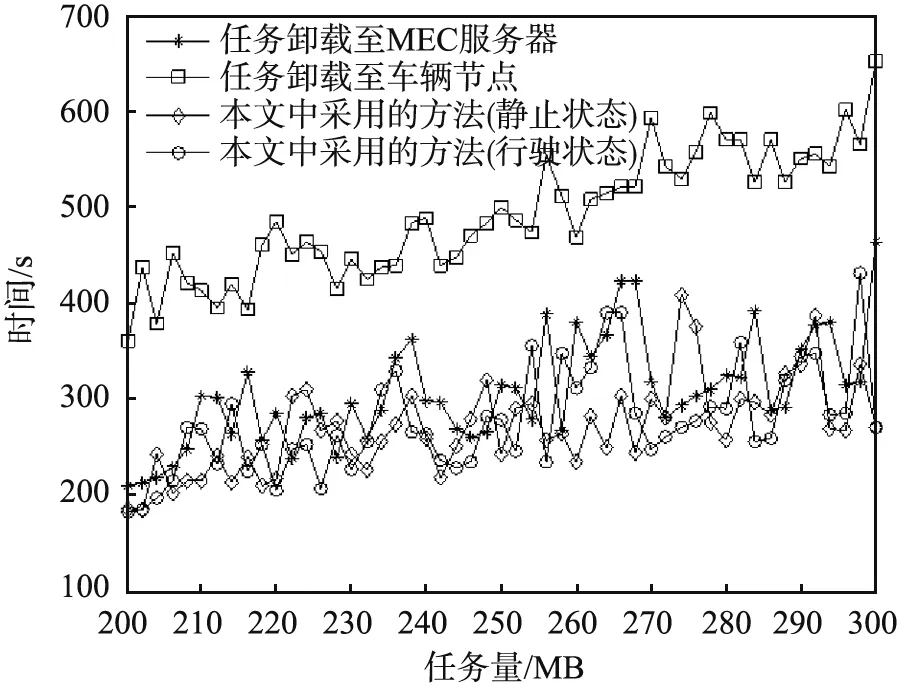
(a)不同任务量

(b)不同时间段 MEC—移动边缘计算。图4 不同任务量、时间段时资源分配和任务卸载的总时长

从图4(a)中可以看出，不同任务量时，任务卸载至车辆节点用的时长明显长于其他2种任务卸载方法所用时长，并且本文中采用的马尔科夫优化方法所耗费的总时长最短。在资源分配和任务卸载过程中，3种方法的总时长均随着任务资源容量的增加而缓慢增加。此外，当车辆处于静止状态时，任务分别卸载至本地相邻车辆节点和MEC服务器的总时长短于车辆处于行驶状态时的总时长，原因是车辆处于行驶状态受到地理环境、行驶速度等多方面的影响，造成传输速度和通信的不稳定。

从图4(b)中可以看出，车辆高速移动性使得任务仅卸载至车辆节点所耗费的总时长随MEC服务器传输速度增大而浮动，不能很好地反映网络传输速度和任务卸载之间的关系；随着MEC服务器传输任务速度的增大，任务传输时间逐渐减少，任务仅卸载至MEC服务器和分别卸载至MEC服务器、车辆节点所用的总时长也呈递减趋势，并且本文中采用的方法任务执行总时长最短。

5 总结

本文中研究了MEC环境中车载网络任务资源分配和卸载问题，构建了描述资源分配和任务卸载路径方案的MEC车载网络系统模型，考虑不同任务的计算需求，将任务资源按不同比例分配至车辆节点和MEC服务器，通过马尔科夫优化过程选择资源分配和任务卸载联合最优方案。仿真实验表明，本文中采用的资源分配和任务卸载马尔科夫优化方法节省了任务执行总时长，能够合理利用网络资源，提高效率。