放电等离子烧结电场下Ni-Al体系FCC相的扩散行为
2021-11-10王飞刘钰玲都昌发闵倩辉刘辉新文诗艺杜勇
王飞,刘钰玲,都昌发,闵倩辉,刘辉新,文诗艺,杜勇
放电等离子烧结电场下Ni-Al体系FCC相的扩散行为
王飞1,刘钰玲1,都昌发2,闵倩辉1,刘辉新1,文诗艺1,杜勇1
(1. 中南大学 粉末冶金国家重点实验室,长沙 410083;2. 中南大学 数学与统计学院,长沙 410083)
采用熔炼法制备Ni-9Al(摩尔分数,%)合金和纯Ni,然后组成Ni/Ni-Al/Ni FCC单相扩散偶在放电等离子烧结炉中进行扩散退火,结合电子探针显微分析(electronic probe micro analysis,EPMA),得到Ni-Al体系FCC相在1 173~1 373 K时SPS电流作用下扩散后的成分距离曲线(即Al含量分布曲线),并采用Sauer-Freise方法与经验公式计算扩散系数,同时基于无外场影响下的原子移动性参数模拟无电流作用的成分距离曲线并计算扩散系数。将模拟的成分距离曲线与实验得到的成分距离曲线进行对比。结果表明,电流对Ni-Al合金原子扩散存在促进作用。电流方向对Ni-Al合金扩散无明显影响,不同电流方向下的成分距离曲线与扩散系数重合度高,故电迁移对Ni-Al合金扩散的影响可忽略。施加电流对扩散频率因子影响不大,但使扩散激活能明显降低。
SPS;扩散偶;Ni-Al;扩散系数;原子移动性参数;电迁移
放电等离子体烧结(spark plasma sintering,SPS)作为一种电流辅助烧结技术,具有升温速度快、烧结时间短、致密化速率高等优点[1],已广泛应用于功能梯度材料、磁性材料和非晶材料的制备。SPS与其他传统烧结技术的显著区别在于引入脉冲电流。SPS中的脉冲电流能显著加快原子扩散速率[2],但其作用机理目前仍不清晰。对于SPS机理的深入研究,需要从微观角度探究电流对原子扩散的作用。基于ARRHENIUS[3]方程形式的扩散系数方程,学术界对于电场促进原子扩散的机理有以下2种主流的解释:1) 电场可显著提高空位浓度,加快原子跳跃的频率,从而影响频率因子。2) 根据电迁移理论,电场存在电子风效应,定向流动的电子流通过碰撞,将动量转移给原子,从而降低扩散激活能[4]。GARAY等[5]研究了Ni-Ti体系的反应扩散动力学,发现在电流密度为2 546 A/cm2的直流电作用下NiTi2金属间化合物相的扩散系数是无电流作用下的43倍。LI等[2]测定了Fe-Al扩散偶在773~873 K下的扩散系数,发现873 K下施加脉冲电流的扩散系数比无电流时增大46倍。LI等[2]认为电流的增强作用主要在于点缺陷密度增大。ZHAO等[6]研究发现,当有密度为800 A/cm2的电流通过时,Cu-Ni体系互扩散的扩散激活能比无电流时降低50%。DENG等[7−8]研究了不同电流密度和电流方向下W-Ti和W-Co体系的互扩散动力学,结果表明不同电流方向下的扩散层厚度存在明显差异,说明存在电迁移现象。之前已有人通过实验验证了电场可增强原子扩散,并进行了理论分析,为外加电场下扩散理论的发展提供了坚实的实验支撑与理论基础。但很少有人研究扩散系数随成分的变化,以及通过计算模拟结合实验分析来研究电场对扩散行为的影响。
Ni-Al体系是镍基高温合金体系的重要子体系。镍基高温合金具有优异的抗氧化性能和抗蠕变疲劳特性,广泛应用于现代涡扇发动机的热端部件中[9]。Al是镍基高温合金中重要的添加元素,Al与基体Ni反应生成金属间化合物相,可提高合金的抗氧化性能和耐腐蚀性能[10]。SPS技术可用于制备Ni基高温合金,虽然目前二元合金的热力学与动力学模型十分完备,已建立的热力学及动力学数据库能准确预测二元合金单相,如FCC相的扩散行为,但对于外加电场下扩散行为的理论与实验研究寥寥无几。本文作者制备Ni/ Ni-Al/NiFCC单相扩散偶,在放电等离子烧结炉中扩散退火,得到Ni-Al合金FCC相1 173~1 373 K下受SPS电流影响的成分距离曲线,并分别用Sauer-Freise方法[11]和经验公式[12]计算扩散系数,研究电流和电流方向对扩散行为的影响,并对影响机理进行分析,为建立外加电场下扩散动力学数据库提供理论依据。
1 实验
基于DUPIN等[13]的热力学参数计算的Ni-Al体系二元相图,确定Ni-Al合金的名义成分为Ni-9Al(摩尔分数,%),该成分处于FCC单相区内。
采用熔炼法制备Ni-9Al 合金和纯Ni,所用原料为纯镍(纯度为99.99%)和纯铝(纯度为99.999%),均为直径和高度均为3 mm的圆柱形颗粒。在电弧熔炼炉中进行熔炼,充高纯氩气作保护气氛。每个合金均反复熔炼4遍,以保证合金成分均匀。采用钼丝线切割,将熔炼后的Ni-9Al合金和纯Ni制成直径8.0 mm、厚度2.0 mm的圆片,封入真空石英管内,在1 473 K下均匀化退火7天,使合金晶粒长大,减小晶界扩散的影响,同时使合金成分更均匀。均匀化退火后的Ni- 9Al 合金和纯Ni样品经淬火、磨制、抛光等处理后,按照从上到下依次为纯Ni片、Ni-Al合金片与纯Ni片的顺序叠放成三明治结构的扩散偶,装入石墨模具内,在放电等离子烧结炉(SPS-3.20MKII)中进行扩散退火,然后通水冷却。退火条件(温度、电流和时间)见表1,其中的电流与设定温度相关,由机器自动调节,电流密度由电流除以样品横截面积确定。保温过程中SPS温度保持不变,电流趋向平稳。退火过程中充高纯氩气做保护气氛。SPS脉冲电流的通断时间比为12:2。
扩散退火后的扩散偶样品经镶样和磨制抛光后,进行电子探针显微分析(electronicprobe microanalysis。EPMA,JXA-8530F,JEOL,Japan),得到扩散界面处的背散射电子图像与不同温度下退火后的表征Al元

表1 不同退火条件下的扩散层厚度和扩散系数
素含量变化的成分距离曲线。
2 计算模型
采用Boltzmann方程[14]对实验获得的成分距离曲线进行拟合,得到Al元素的摩尔分数与扩散距离的函数表达式。Boltzmann方程如下:

式中:1和2分别为扩散偶两端元素的摩尔分数;0为Matano面即扩散通量为零的平面的位置;为扩散距离。
在得到成分距离函数表达式后,采用Sauer- Freise方法计算Ni/Ni-Al/Ni FCC相扩散偶在不同温度下和不同成分处的扩散系数。计算公式如下:
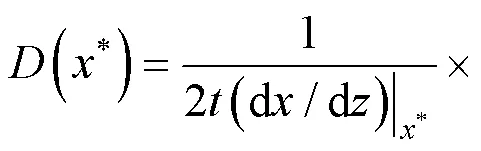

式中:为互扩散系数;*表示某一位置;为SPS扩散退火保温时间;min和max分别为扩散偶两端Al元素摩尔分数的最小和最大值。
扩散系数计算过程中用到的每一组参数,其误差均会通过扩散系数计算方程传递到扩散系数中,误差传递方程[15]的表达式如下:

式中:,,…为函数的相关量;()是变量的误差;是成分等变量。
根据扩散层厚度与扩散时间,由以下经验公式得到一定成分范围内的平均扩散系数:

式中:为扩散层厚度;为互扩散系数;为扩散 时间。
传统热激活扩散满足Arrhenius方程:

式中:0为扩散频率因子;为扩散激活能;为气体常数;为热力学温度。将式(4)转换为对数形式:

ln与1/呈线性关系,由ln与1/的关系曲线斜率和截距获得扩散频率因子0与扩散激活能。
3 结果与讨论
3.1 成分距离曲线
图1所示为EPMA得到的在1 373 K/3 600 s条件下退火处理后的Ni/Ni-9Al/Ni扩散偶的扩散界面背散射电子图像。扩散界面只有一种衬度,表明整个扩散界面无第二相存在,从而验证扩散偶为单相。图2所示为在不同电流方向和不同退火条件下退火后的成分距离曲线。图中2条虚线为依据DENG等[7]报道的方法确定的扩散开始与结束的位置,用来确定扩散距离。“Ni→Ni-Al”表示电流从纯Ni流向Ni-Al合金,“Ni-Al→Ni”表示电流从Ni-Al合金流向纯Ni。为了研究SPS退火对扩散偶扩散行为的影响,需得到无电流影响的成分距离曲线与扩散系数。采用基于CAPLHAD方法的原子移动性参数[16]模拟无电流作用下的成分距离曲线并计算扩散系数。所用Ni-Al体系的热力学信息来自DUPIN等[13]的研究。ZHANG等[17]评估了Ni-Al体系FCC相的互扩散系数,并优化得到一套自洽的原子移动性参数。CHENG等[18]与XU等[19]分别采用ZHANG等[17]评估的Ni-Al原子移动性参数预测FCC相Ni-Al-Mn和Ni-Al-Nb三元系的扩散系数,理论值与实验值吻合较好。表明ZHANG等[17]的数据具有相当的可靠性,可用于模拟无电流下的Ni-Al体系FCC相扩散行为。本文作者基于文献[13, 17]报道的热力学数据及原子移动性参数,用CALTPP (CALculation of ThermoPhysical Properties)软件[20]模拟Ni-Al合金分别在1 173 K/5 400 s、1 273 K/4 800 s和1 373 K/3 600 s条件下无电流作用退火后的成分距离曲线,结果如图3、4和5所示,图中还包含实验测定的同一温度不同电流方向下的成分距离曲线,并将同一退火温度下所有成分距离曲线Matano平面的位置设为一致,用于直观地比较电流的存在及其方向对扩散行为的影响。无电流作用下,FCC相Ni-Al合金在1 173 K下退火5 400 s后的扩散距离约为10 μm,SPS电流作用下的扩散距离约为28 μm,电流作用下的扩散距离较无电流时有成倍的提高。不同电流方向下的成分距离曲线近似重合。图4和图5呈现与图3相同的规律。因此从成分距离曲线可看出,在SPS电场下退火,Al原子的扩散速率显著提高,不同电流方向下的扩散速率无明显区别,这表明SPS退火对Ni-Al合金的原子扩散具有明显的增强作用,但电流方向对扩散的影响可忽略。

图1 Ni/Ni-9Al%扩散偶在1 373 K/3 600 s条件下退火后的背散射电子图像

图2 实验测定的Ni/Ni-Al/Ni扩散偶扩散退火后的Al含量分布及其拟合曲线
(a) 1 173 K for 5 400 s, the current flows from pure Ni to Ni-Al alloy; (b) 1 173 K for 5 400 s, the current flow from Ni-Al alloy to pure Ni; (c) 1 273 K for 4 800 s, the current flow from pure Ni to Ni-Al alloy; (d) 1 273 K for 4 800 s, the current flow from Ni-Al alloy to pure Ni; (e) 1 373 K for 3 600 s, the current flow from pure Ni to Ni-Al alloy; (f) 1 373 K for 3 600 s, the current flow from Ni-Al alloy to pure Ni

图3 实验测定及模型预测的Ni/Ni-9Al/Ni扩散偶在1 173 K下退火5 400 s后的成分距离曲线
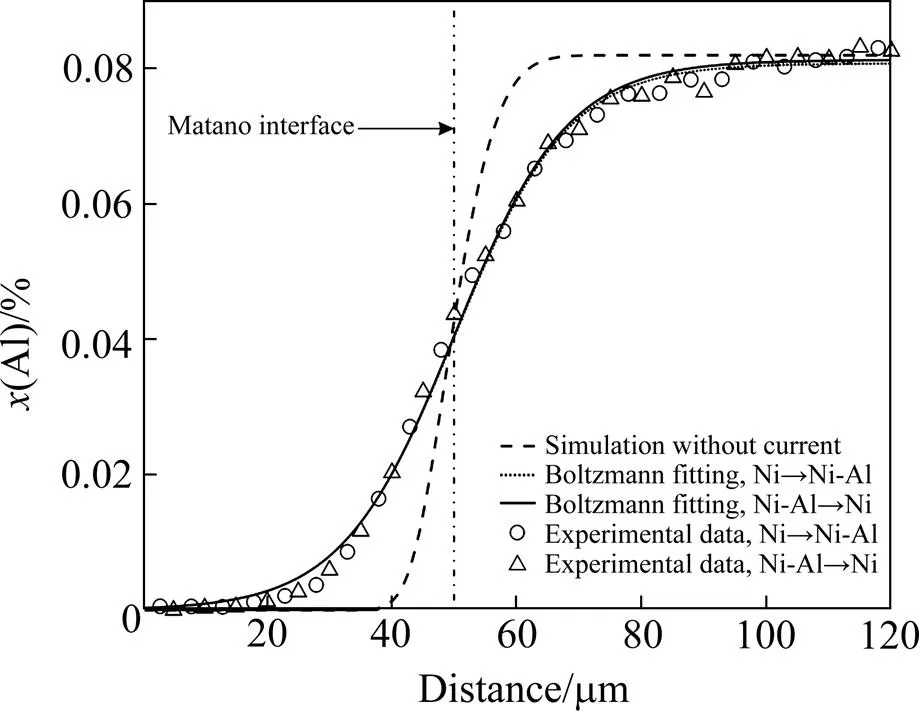
图4 实验测定及模型预测的Ni/Ni-8Al/Ni扩散偶在1 273 K下退火4 800 s后的成分距离曲线

图5 实验测定及模型预测的Ni/Ni-9Al/Ni 扩散偶在1 373 K下退火3 600 s后的成分距离曲线。
3.2 基于Sauer-Freise方法计算扩散系数
扩散系数表示单位浓度梯度下的扩散通量,是描述元素扩散快慢的物理量。基于菲克定律的Sauer- Freise方法广泛应用于二元系单相合金扩散系数[14, 21]的计算。Sauer-Freise方法以成分、距离和扩散时间作为输入项,可准确得到随成分变化的扩散系数。式(4)所示经验公式广泛应用于W-Ti[7]、Cu-Ti[22]、Fe-Al[2]等体系外加电场下扩散系数的计算,仅需提供扩散层厚度与扩散时间,便可得到一定成分范围内的平均扩散系数。本研究分别采用Sauer-Freise方法和式(4)计算扩散系数,然后基于Arrhenius方程计算扩散相关的2个参量,即扩散频率因子0与扩散激活能,以此分析电流增强扩散的机理。
图6所示为利用Sauer-Freise方法计算的1 173/ 5 400 s、1 273/4 800 s和1 373 K/3 600 s和不同电流方向下的扩散系数,以及参数模拟的无电流下的扩散系数。依据误差传递方程(式(3))计算实验及计算造成的扩散系数的误差。由图可知,无电流作用下的扩散系数随Al含量增加而增大;而在外加电场作用下,随Al含量增加,扩散系数变化不明显。扩散系数的误差呈现两端高中间低的趋势。考虑误差影响下,电流作用下的扩散系数比无电流下增大将近一个数量级,说明电流作用下扩散系数提高不是误差因素带来的,这证明了电流对扩散系数存在显著影响。电流作用下的扩散系数比无电流下的增大幅度随Al含量增加而减小,这是由于电流对Al原子扩散的加速作用随Al含量增加而减小。从图中还看出不同电流方向下的扩散系数基本一致,这进一步证明电流方向对FCC相Ni-Al合金的扩散无显著影响。而根据电迁移理论,电流使原子扩散速率加快,本质上是电子流在流动方向上与定向迁移的金属原子发生碰撞导致原子扩散速率加快,因而这种加速作用具有明显的方向性。而本研究结果表明,在不同电流方向下的成分距离曲线与扩散系数均呈现高度的一致性,所以认为FCC相Ni- Al合金在1 173~1 373 K下的电场增强扩散行为中,电迁移效果不占主导作用。

图6 不同电流方向下Ni-Al合金FCC相扩散系数的比较
根据不同温度下的扩散系数,绘制ln−1/散点图,根据式(5)所示Arrhenius公式的变形(式(6))进行线性拟合,拟合直线的斜率等于−/,截距为ln0,进而得到不同成分处的扩散频率因子0和扩散激活能并与WATANABLE等[23]基于扩散偶法与EPMA的实验数据进行比较如图7和8所示。扩散频率因子与扩散激活能的误差值均较大,可能是由于扩散系数误差或者电流作用,使得扩散系数与温度关系偏离Arrhenius公式。由图7可见本文计算的扩散频率因子与文献值差距不大,且文献值处在计算值误差范围内,这表明电流作用下的扩散频率因子与无电流下的值无明显差异。图8中不同电流方向下的扩散激活能相近,一致性较高,这表明电流方向对扩散激活能无明显影响。而通电流条件时的扩散激活能比文献报道的无电流时的扩散激活能降低15~28 kJ/mol,差距明显,因此认为外加电流可能使Ni-Al合金的扩散激活能显著降低,这与ZHAO等[6]对于Cu-Ni体系的研究结果 一致。
3.3 基于经验公式计算扩散系数
根据扩散层厚度及退火时间,利用经验公式计算Ni-Al体系在不同温度和不同电流密度下的扩散系数,结果列于表1。由表可知,在相同退火温度下,不同电流方向下的扩散层厚度差距极小,扩散系数也很接近。这一结果表明电流方向对扩散速率的影响可忽略不计。绘制ln−1/曲线,如图9所示,由此得到不同电流方向下的扩散频率因子0与激活能。同电流方向下退火的扩散激活能分别为200.6和206.6 kJ/mol,显著低于无电场作用下的激活能239~250 kJ/mol[23]。需要注意的是,通过经验公式得到的扩散系数与合金成分无关,为一定成分范围内的平均扩散系数,而采用Sauser-Freise方法计算与原子移动性参数模拟的扩散系数均随成分变化而变化。因此认为经验公式可作为估算扩散系数的快捷手段,但它不能准确反映Ni-Al体系FCC相扩散系数随成分变化的趋势。

图7 当前工作计算的互扩散频率因子与文献值[23]的比较

图8 当前工作计算的互扩散激活能与文献值[23]的比较
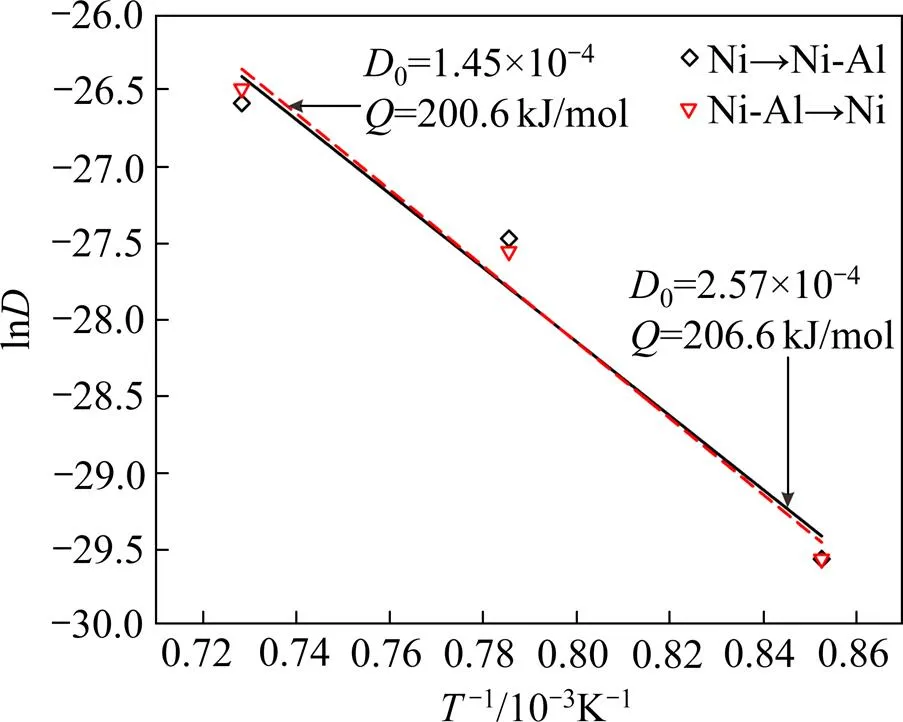
图9 不同电流方向下Ni-Al体系FCC相互扩散激活能与频率因子
>Fig.9 The interdiffusion activation energy and pre-exponential factor of FCC Ni-Al system with different current directions
4 结论
1) Ni-Al体系FCC相在电流作用下的扩散距离比无电流影响下增长3~4倍,说明施加电流能够增强原子扩散速率。
2) 电流方向对扩散行为无明显影响,说明电迁移现象对Ni-Al合金FCC相的电场增强扩散行为无明显影响。
3) 扩散频率因子0受电流以及电流方向影响较小。电流作用下的扩散激活能则较无电流时明显降低,因此认为电场增强FCC相Ni-Al合金扩散的主要机理为电流导致激活能降低。
[1] 黄伯云, 韦伟峰, 李松林, 等. 现代粉末冶金材料与技术进展[J]. 中国有色金属学报, 2019, 29(9): 1917−1933.
HUANG Boyun, WEI Weifeng, LI Songlin, et al. Modern powder metallurgy materials and technology progress[J]. Chinese Journal of Nonferrous Metals, 2019, 29(9): 1917−1933.
[2] LI R D, YUAN T C, LIU X J, et al. Enhanced atomic diffusion of Fe-Al diffusion couple during spark plasma sintering[J]. Scripta Materialia. 2016, 110: 105−108.
[3] ARRHENIUS S. Chemical reaction velocities[J]. Zeit Physikal Chem, 1899, 28: 317–335.
[4] BLECH I A. Electromigration in thin aluminum films on titanium nitride[J]. Journal of Applied Physics, 1977, 47(4): 1203−1208.
[5] GARAY J E, TAMBURINI U A, MUNIR Z A. Enhanced growth of intermetallic phases in the Ni-Ti system by current effects[J]. Acta Materialia, 2003, 51(15): 4487−4495.
[6] ZHAO J F, GARAY J E, TAMBURINI U A, et al. Directional electromigration-enhanced interdiffususion in the Cu-Ni system[J]. Journal of Applied Physics, 2007, 102(11): 114902.
[7] DENG S H, YUAN T C, LI R D, et al. Influence of electric current on interdiffusion kinetics of W-Ti system during spark plasma sintering[J]. International Journal of Refractory Metals and Hard Materials, 2018, 75: 184−190.
[8] DENG S H, LI R D, YUAN T C, et al. The preferential growth behaviors of the intermetallics at the W/Co interface during spark plasma sintering[J]. Applied Physics Letters, 2020, 117(19): 194102.
[9] ROGER C R. The Superalloys (Fundamentals and Applications)[M]. London: Cambridge University Press, 2006: 33−120.
[10] 王君. 镍基高温合金在航空发动机中的应用[J]. 中国新通信, 2019, 21(1): 221−222.
WANG Jun. Application of Nickel-based superalloy in aero- engine[J]. China New Communications, 2019, 21(1): 221− 222.
[11] SAUER F, FREISE V. Diffusion in binary mixtures with volume change[J]. Z Electrochem, 1962, 66: 352−363.
[12] GUILLEMOT F, BOLIVEAU M, BOHN M, et al. On the diffusion in the Mo-Ta refractory system[J]. International Journal of Refractory Metals and Hard Materials, 2001, 19(3): 183−189.
[13] DUPIN N, ANSARA I, SUNDMAN B. Thermodynamic re-assessment of the ternary system Al-Cr-Ni[J]. Calphad, 2001, 25(2): 279−298.
[14] MIN Q H, LIU Y L, DU Y. Interdiffusion and atomic mobilities in FCC Ag-Mg and Ag-Mn alloys[J]. Calphad, 2019, 65: 93− 100.
[15] LECHELLE J, NOYAU S, AUFORE L, et al. Volume interdiffusion coefficient and uncertainty assessment for polycrystalline materials, Diffus[J]. Fundam Org, 2012, 17(2): 1−39.
[16] JÖNSSON B. Ferromagnetic ordering and diffusion of carbon and nitrogen in bcc Cr-Fe-Ni alloys[J]. Zeitschrift Fur Metallkunde, 1994, 85(7): 498−501.
[17] ZHANG L J, DU Y, CHEN Q, et al. Atomic mobilities and diffusivities in the FCC, L12and B2 phases of the Ni-Al system[J]. International Journal of Materials Research, 2010, 101(12): 1461−1475.
[18] CHENG K M, LIU D D, ZHANG L J, et al. Interdiffusion and atomic mobility studies in Ni-rich FCC Ni-Al-Mn alloys[J]. Journal of Alloys and Compounds, 2013, 579: 124−131.
[19] XU G H, LIU Y J, KANG Z T. Mobilities, interdiffusivities and their kinetic implications for fCC Ni-Al-Nb alloys[J]. Journal of Alloys and Compounds, 2017, 709: 272−276.
[20] LIU Y L, ZHANG C, DU C F. CALTPP: a general program to calculate the thermophysical properties[J]. Journal of Material Science & Technology, 2020, 42: 229−240.
[21] LIU H X, LIU Y L, DU Y, et al. Atomic mobilities and diffusivities in FCC Co-X (X = Mn, Pt and Re) alloys[J]. Calphad, 2019, 64: 306−312.
[22] YANG C, MO D G, LU H Z, et al. Reaction diffusion rate coefficient derivation by isothermal heat treatment in spark plasma sintering system[J]. Scripta Materialia, 2017, 134: 91− 94.
[23] WATANABE M, HORITA Z, FUJINAMI T, et al. Application of analytical electron microscopy to diffusivity measurement in NiAl System[J]. Defect and Diffusion Forum, 1993, 95/98: 579− 586.
Diffusion behavior of FCC Ni-Al system in spark plasma sintering electric field
WANG Fei1, LIU Yuling1, DU Changfa2, MIN Qianhui1, LIU Huixin1, WEN Shiyi1, DU Yong1
(1. State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China; 2. School of Mathematics and Statistics, Central South University, Changsha 410083, China)
The smelting method was employed to prepare the Ni-9Al (mole fraction, %) alloys and pure Ni, and then the Ni/Ni-Al/Ni diffusion couples were annealed for diffusion in spark plasma sintering (SPS). The concentration profiles of FCC Ni-Al system at 1 173−1 373 K under the effect of SPS current were obtained combining with electronic probe microanalysis (EPMA). The Sauer-Freise method and empirical formula were employed to calculated diffusion coefficients respectively. The concentration profiles without current were simulated based on the atomic mobilitiy parameters without the influence of applied field and then the diffusion coefficients were calculated meanwhile. Comparing the simulated concentration profiles with the experimental ones. The results show that the current promotes the diffusion of Ni-Al alloys. The direction of the current has negligible effect on the diffusion of Ni-Al alloys. The concentration profiles and diffusion coefficients under different current directions have a high degree of overlap, indicating that the influence of electromigration on the diffusion of Ni-Al alloy is negligible. The applied current has little effect on the diffusion frequency factor, while the applied current significantly reduces the diffusion activation energy.
SPS; diffusion couples; Ni-Al; diffusion coefficients; atomic mobility; electromigration
TG113.12
A
1673-0224(2021)05-412-07
国家自然科学基金资助项目(51671219)
2021−04−05;
2021−04−30
刘钰玲,讲师,博士。电话:18711084610;E-mail: liu.yuling@csu.edu.cn
(编辑 汤金芝)
