基于强度折减法考虑三维地震作用的边坡稳定分析

田苗旺，王 刚

(中科路恒工程设计有限公司,山西 太原 030006)

0 引言

目前针对地震荷载作用下边坡稳定性分析主要采用的是拟静力分析方法,包括我国相关规范[1],均引入地震惯性力进行静力计算,该方法指导工程应用方便,但无法反映边坡的动力特性。目前国内外学者主要采用基于强度折减法的有限元[2]、离散元[3]计算软件,通过先静力后动力方法[4]来模拟边坡在地震作用下的响应,从而对其破坏机制、破坏面及稳定安全系数[5-7]进行研究分析。以上方法采用动力分析方法可考虑边坡的动力特性来评价边坡稳定,但大多都将模型简化为平面应变二维模型,地震采用仅考虑一维作用,未考虑三维模型的空间效应和地震的多维作用,与实际情况存在一定差距。故本文采用强度折减法,对二维、三维边坡模型在重力荷载、一维及三维地震作用下的响应进行分析,并得到三维边坡的破坏机制以及边坡的稳定安全系数。

1 强度折减法与边坡稳定判别标准

通过对土体材料抗剪强度进行折减,分析折减后边坡内应力场、位移场的特征。当计算不收敛或出现明显贯通滑坡的塑性区时,发生边坡失稳破坏,前一级折减系数即为边坡安全系数。

对于Morh-Coulomb材料,强度折减系数表达式为:

(1)

(2)

(3)

其中,c，φ，ω分别为土黏聚力、内摩擦角、强度折减系数;c′,φ′分别为折减后土黏聚力、内摩擦角。

如何判断边坡的临界状态是强度折减法计算边坡稳定的关键,常用到的判别边坡临界失稳状态的方法有:1)变形特征:关键点位移、关键部位应变;2)应力特征:塑性变形区贯通程度;3)数值计算收敛情况。其中关键点位移、坡体塑性区贯通原则常用于二维平面应变模型的动力分析,本文考虑三维地震作用下的边坡稳定,采用以上三种方法作为边坡临界失稳的判断依据。

2 工程实例及分析条件

2.1 工程实例

某均质土坡高17 m,坡角为49°,地质条件良好。该处的地层主要包括:1)坡积层,以烁粉质黏土为主;2)滑坡堆积层,大多数是粉质黏土,结构较为松散,边坡模型尺寸如图1所示。ABAQUS软件二维平面应变简化模型、三维模型如图2,图3所示,表1为土体参数。

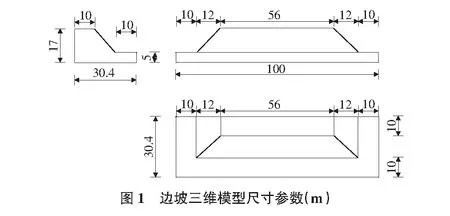
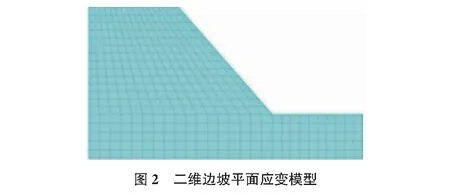
表1 土体参数

2.2 计算模型建立

采取强度折减法先进行重力荷载下的静力计算,边坡土体受力平衡后进行地震动力时程分析。静力分析时,对边坡底部施加固定约束,对土体前后、左右面施加法向位移约束;地震动力时程分析时,在土体底面、侧面施加加速度并释放加速度方向的位移约束。土体参数采用Morh-Coulomb模型,通过分析过程中设置场变量Fs[8],实现快速对Morh-Coulomb模型的摩擦角、黏聚力进行折减,当计算不收敛后对结果进行分析。

2.3 地震波的选取与输入

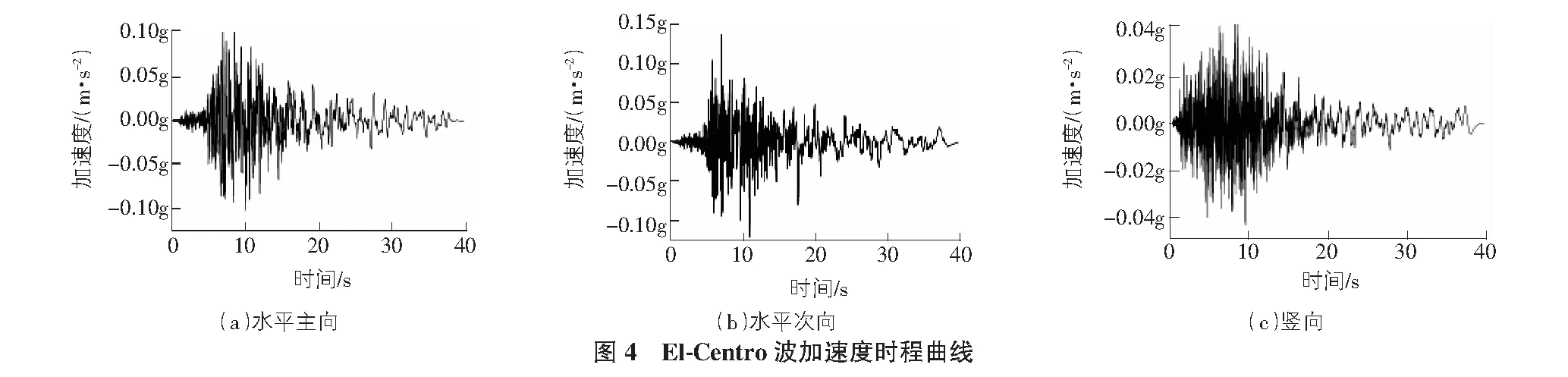
土体的塑性变形随着地震持时的增加而不断变大,本文选取经典El-Centro地震波40 s,其水平、竖直方向的地震波加速度时程曲线如图4所示。仅一维地震动输入时,采取将水平主向加速度沿模型X轴方向输入;三维地震输入时,加速度峰值比例应取主向∶次向∶竖向=1∶0.85∶0.65。地震动水平主向加速度沿着模型X轴方向,水平次向加速度沿着Z轴方向,竖向加速度沿着Y向。地震动力分析时的阻尼取0.15。

3 二维与三维模型模拟结果对比

3.1 仅重力荷载

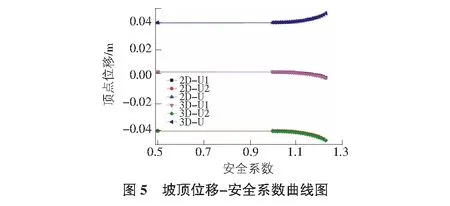
采用理正岩土计算边坡稳定,假定滑裂面为圆弧形,自动搜索最危险滑裂面,采用瑞典条分法,简化Bishop,Janbu法计算得到土坡稳定系数分别为1.203,1.238,1.241。采用有限元强度折减法对关键点位移分析得二维、三维模型下该边坡的稳定安全系数均为1.23(如图5所示,图中U1,U2,U代表水平向、竖向以及总位移)。仅考虑重力荷载作用下,三维模型与二维模型计算稳定性相同,但二维模型建模简单、计算速度快。

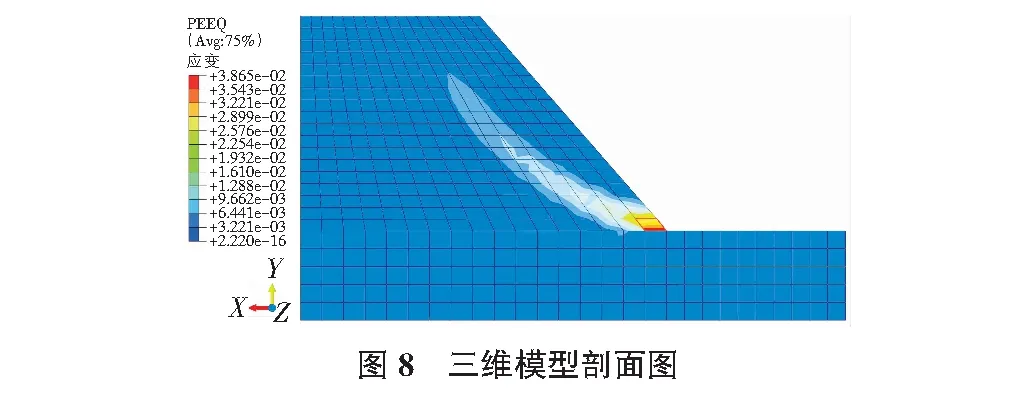
考虑三维模型后,边坡土体的塑性区域在空间上为半个“树叶”(见图6),最不利位置位于边坡坡角中部。随着土体强度折减系数增大,土体的塑性区域沿着破裂面逐渐向上、向两边发展,直至计算不收敛。二维模型的塑性区(如图7所示)与三维边坡模型临界稳定中部剖面的塑性区(如图8所示)形状基本一致,当折减系数为1.230时,二维模型的等效塑性应变最大值0.032 89,三维模型的等效塑性应变最大值为0.038 65,考虑三维模型后塑性应变增大14.1%。

3.2 一维地震作用

边坡土体的静力计算完成后,将El-Centro波水平主向从边坡底部输入,土体强度折减系数取1.23,地震峰值加速度取0.1g,得到二维、三维边坡在一维地震作用下的地震响应。结果表明,二维、三维边坡模型在一维地震作用下,土体内部的塑性区域相似,变化趋势相同。当地震开始时,加速度较小,土体应力变化较小,塑性区域与静力荷载情况下的基本相同,未发生变化。随着地面加速度的逐渐增大,土体内部的塑性区域沿破裂面向上扩散,同时塑性区域的厚度以及数值逐渐增大。二维、三维边坡模型的塑性变形最大值均集中于坡角处,且该处应力最大、水平位移最大。三维边坡模型的塑性区域,随着地震时间增加土体的塑性区域沿着土体的破裂面逐渐向边坡上部、两端发展,直至贯通整个边坡,形成滑裂面失稳破坏。

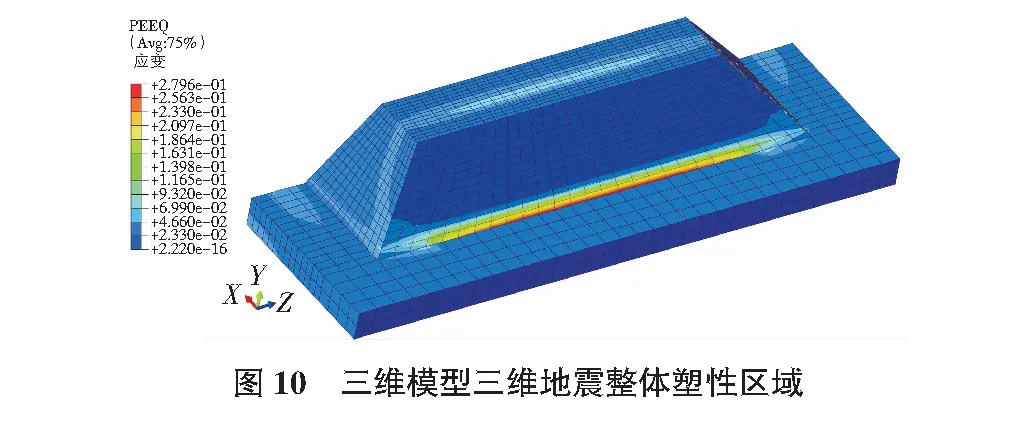
二维边坡计算模拟结果显示,当时间t=24.83 s时,坡顶最大塑性应变达到0.029,边坡塑性区已贯通(如图9所示),根据判断准则,边坡处于临界失稳状态。而三维边坡模型当时间t=8.8 s时(如图10所示),坡顶最大塑性应变达到0.034,塑性区已贯通,塑性区范围比二维边坡塑性区更大,故考虑三维模型的地震响应更大。

3.3 三维地震作用

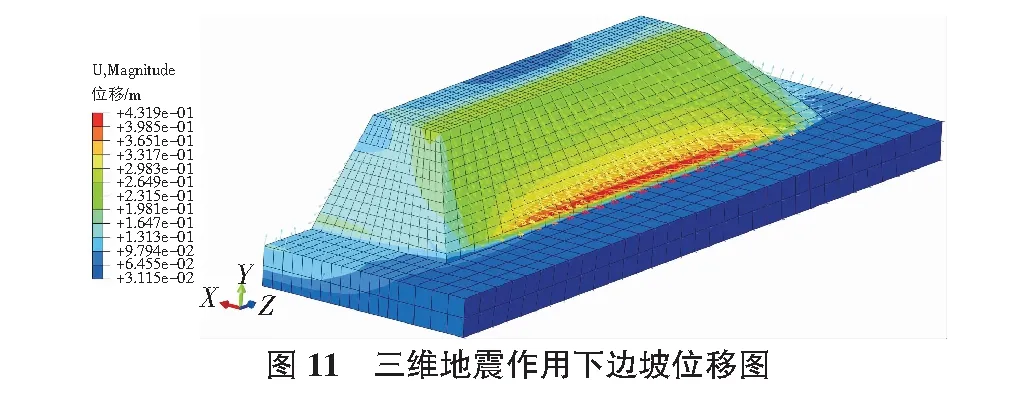
将三维地震动输入三维边坡模型,强度折减系数取为1.23,地震水平主向、次向、竖向峰值加速度分别为0.1g,0.85g,0.65g。模拟结果表明,考虑三维地震作用后,地震响应明显增大,在t=9.06 s时,边坡顶部最大塑性应变达到0.06,塑性区从坡底到坡顶贯通,边坡左右侧的塑性区域也基本贯通边坡左右侧塑性应变值约为0.031,为临界失稳状态。边坡沿着滑裂面开始向下移动,坡底中部位移最大,达到0.43 m(如图11所示)。

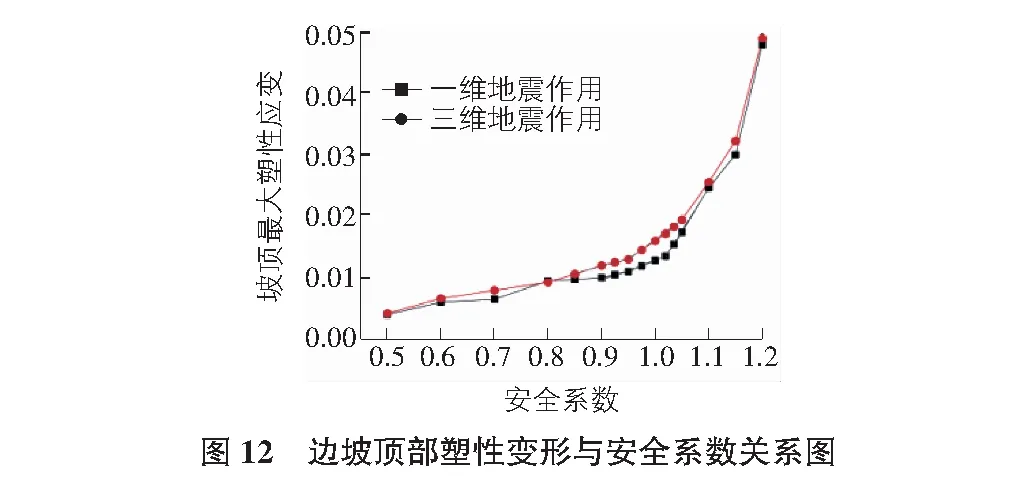
当边坡在地震作用下失稳时,坡顶塑性应变会急剧增大,本文采用坡顶土体应变表征坡体变形特征,如图12所示,可得当考虑三维地震作用后,该边坡的稳定系数由1.23降低至0.95,而只考虑一维地震作用,该边坡的稳定系数降低至1.02,故考虑三维地震作用更加不利。

4 结论

利用ABAQUS软件分析了二维、三维边坡在一维、三维地震作用下的地震响应,得到以下结论:1)当仅考虑重力荷载不考虑地震作用影响时,二维模型计算得到的边坡安全度与三维模型计算得到的边坡安全度相同;2)随着材料强度折减系数增大、地震持续时间增加,三维边坡塑性区域沿着破裂面不断增大,直至坡顶、边坡两端均贯通。一维地震作用下,三维边坡模型得到的地震响应大于二维边坡模型;3)考虑三维地震作用的边坡稳定安全系数比考虑一维地震作用的更低。因此考虑三维边坡的地震稳定性时,应考虑三维地震荷载作用。