悬索面内1/3次谐波共振瞬时相频特性

陈 皓， 孙测世

(重庆交通大学土木工程学院， 重庆 400074)

悬垂缆索在高压输电及桥梁中具有广泛的应用，但其作为高强度、低阻尼的柔性结构，因初始垂度引起的非线性使其力学特性变得复杂[1]，易在风雪等外荷载作用下产生各种次谐波共振，常常引起结构的破坏[2-3]，例如输电线舞动严重时会导致相邻输电线碰撞而产生闪络，甚至使输电系统瘫痪[4-5]，引发广泛关注。

相邻悬索碰撞需要同时满足大幅振动及振动反相，目前各国学者已对悬索的次谐波共振机理开展了大量的研究，但其主要针对不同参数及耦合机理下响应的幅值[6]或某一组参数下响应相位[7-8]，而针对不同参数下悬索响应相位的研究较少。已有研究结果表明，悬索响应与激励相位差与激励频率密切相关[9]。与之类似，文献[10]进行了斜拉桥全桥模型试验，在主梁跨中施加竖向简谐激励，观测到两根相邻斜拉索发生异步的大幅振动，通过扫频试验得到两者稳态振动的相位差随激励频率的变化曲线。对于多模态而言，Hu等[11]的研究表明斜拉索不同模态间同样存在相位差，且随激励频率变化而改变。而结构参数差异同样会对其相频特性产生较大影响，赵珧冰等[12]、黄超辉等[13]研究发现温度变化会引起系统非线性共振响应特性发生定性和定量的变化，对共振响应区间及相位产生直接影响。此外，开展对悬索响应相位的研究是后续开展辅助索减振研究的基础之一，研究表明，当相邻索之间出现反相振动时，辅助索减振效果良好，而同相振动时其作用很小[14]。

综上，激励频率及参数差异会对悬索响应相位产生较大影响，而垂跨比对于悬索而言为非常重要的结构参数。因此，现研究不同垂跨比下悬索发生面内1/3次谐波共振的响应与激励的瞬时相位差的随垂跨比及激励频率的变化规律，并着重分析高阶项及漂移项成分的影响。

1 力学模型

建立图1所示悬索非线性动力学模型，为简化计算，做出以下假设：①悬索的静力平衡曲线为二次抛物线；②忽略悬索的抗弯、剪切及抗扭刚度；③悬索在振动过程中处于弹性变形范围。悬索振动采用局部坐标O-xyz来描述：坐标原点O，x为悬索弦线方向，y为索面内垂直弦线的方向，x、y方向对应位移分别用u、w表示，l为索长。

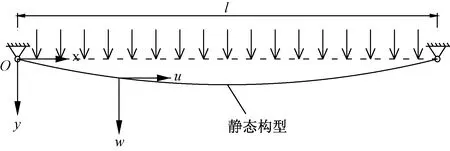
图1 分布面内激励下悬索振动简化模型Fig.1 Simplified model of suspension cable vibration under in-plane excitation

1.1 控制方程

考虑拉索初始垂度与几何非线性，悬索两端铰接。通过利用Hamilton原理得到分布面内激励下悬索面内非线性振动力学方程[15]为

(1)

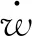
y=4fx(1-x)

(2)

式(2)中：f为垂跨比。

设拉索以拟静态方式进行轴向振动，略去高阶无穷小量，拉索无量纲控制方程为

(3)

采用的无量纲变换有

为了方便书写，省去“*”号。

1.2 离散化模型

在分布外激励作用下，悬索振动位移被认为是由纯振动产生，因此令

(4)

式(4)中：φn为模态函数；qn为广义坐标函数。

正对称模态函数为

(5)

式(5)中：ωn为悬索n阶固有频率。

(6)

反对称模态函数为

(7)

利用Galerkin方法得到

(8)

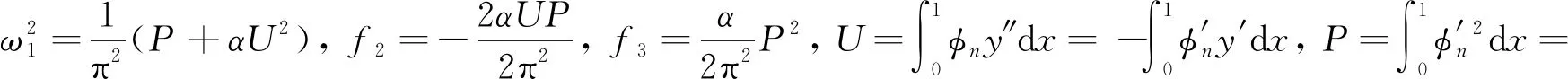
1.3 摄动分析

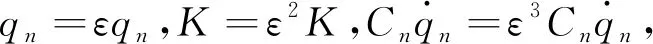
qn(T0,T1,T2)=q0(T0,T1,T2)+εq1(T0,T1,T2)+ε2q2(T0,T1,T2)+…

(9)

式(9)中:Tn=εnt(n=0,1,2,…)，将式(9)代入式(8)，并按照ε的幂次进行整理，可以得到下列方程。

(10)

(11)

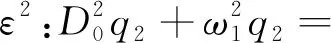
(12)

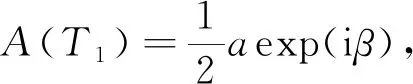
(13)

(14)

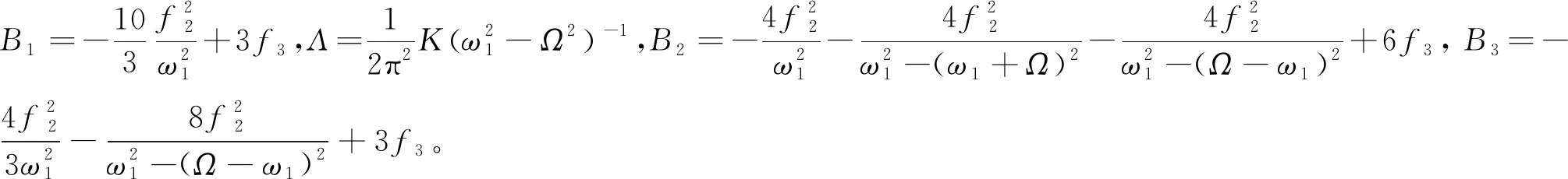
设γ=σT0-3β，令a′=γ′=0，此时幅频响应方程的表达式为

(15)

面内运动方程的二阶近似解为

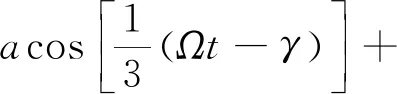
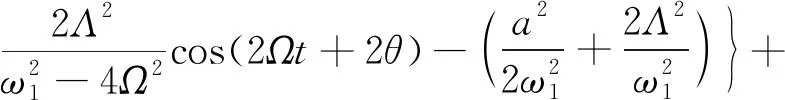
(16)

式(13)中：O(ε2)为高阶无穷小量。

由式(16)可知，近似解由线性项、高阶项和漂移项三部分组成，由于高阶项及漂移项的影响，其瞬时相频特性变得复杂，为便于后文分析，定义为

(17)

2 数值算例

利用MATLAB进行数值计算，得到不同垂跨比下悬索瞬时相频特性的变化规律。算例分析中悬索各项物理参数如表1所示，另外无量纲化后的激励幅值和阻尼系数分别为0.02和0.005。

结合悬索参数，根据式(12)得到了悬索垂跨比为0.006及0.01时的幅频响应曲线，并将结果与文献[16]进行了对比，结果如图2所示。可以看出，两者结果大体吻合，但略微有一定差异，当垂跨比为0.006时，两者的最大误差为6.0%，而当垂跨比为0.010时，两者的最大误差为1.4%。

表1 悬索参数[16]Table 1 Suspended cable parameters[16]

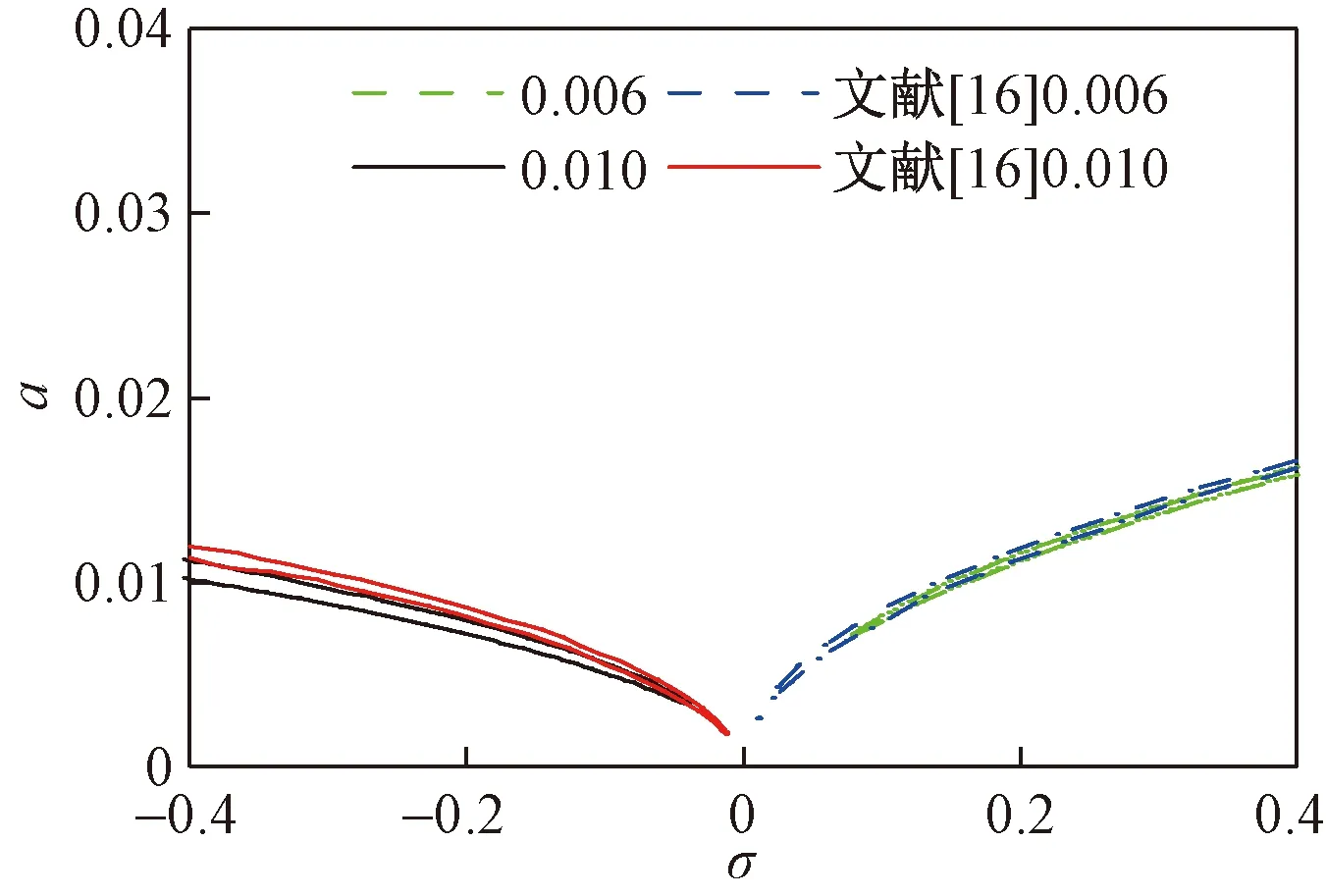
图2 幅频响应曲线Fig.2 Amplitude-frequency response

2.1 不同垂跨比下响应与激励的瞬时相位差

为研究垂跨比对悬索瞬时相频特性的影响，首先研究不同垂跨比悬索在单个激励频率下的响应。文献[18]表明垂跨比的大小在非线性动力学分析特性时非常重要，根据其选择4种垂跨比分别为0.008 5、0.010、0.015、0.02，对应悬索固有频率分别为1.155、1.242、1.669、2.211，为满足1/3亚谐波共振，确定激励频率的方式采用固定的调谐参数-0.5。对于次谐波共振而言，每种垂跨比下的悬索均会对应两个非平凡解，但重点不在于分岔问题，因此不区分解的稳定，仅取其中一个解进行分析。

图3为4种垂跨比下的响应时程曲线，因不同垂跨比的悬索对应的激励频率不同，导致不同悬索之间的响应幅值及周期相差较大，但很明显可以看出，当f=0.008 5和f=0.01时，其响应的时程曲线呈现“上宽下窄”，且整个曲线向上漂移，而垂跨比为0.015和0.02时的响应时程曲线较为接近正弦波的形式。

对悬索响应及激励的时程曲线分别进行Hilbert变换，得到响应与激励的瞬时相位差时程曲线，如图4所示。

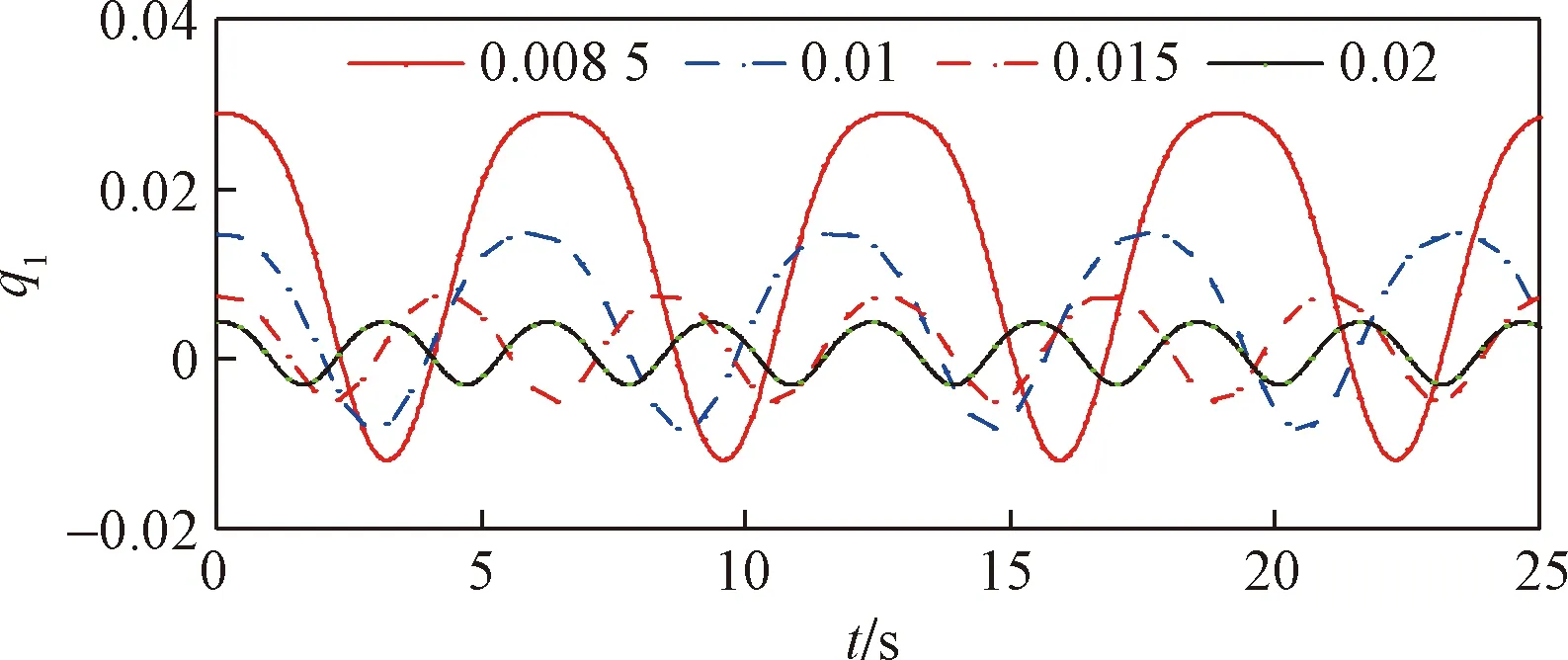
图3 响应时程曲线Fig.3 Response time history

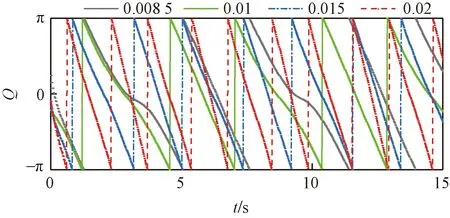
图4 响应与激励的瞬时相位差时程曲线(σ=-0.5)Fig.4 Time history of transient phase difference between response and excitation (σ=-0.5)

各悬索响应与激励瞬时相位差值呈周期性变化，该周期等于与激励周期一致。因悬索与激励满足1/3亚谐波共振，两者在同一个响应周期内会出现两次反相的状态，即该差值在一个周期内会出现2次接近-π的情况。对比各悬索发现，当f=0.008 5和f=0.01时，一个振动周期内部明显分为两个时长不等的递减区间，且当f=0.008 5时，瞬时相位差在周期内的变化速率会由快变慢再变快，而其余3种垂跨比下瞬时相位差均迅速降低且变化速率无明显变化，结合图3和式(13)分析，应是响应中高阶项和漂移项的影响。

2.2 高阶项和漂移项对于响应瞬时相位的影响

为考虑高阶项和漂移项对响应瞬时相位的响应，分别对q1和Q进行Hilbert变换，并定义无量纲参数如下。

(18)

式(18)中：ΔPh为q1和Q的瞬时相位之差，ΔPhmax为ΔPh幅值最大值，对两者无量纲化得到Ph及Phmax。由于q1为系统的全部响应，而Q仅是响应的线性项，因此ΔPh实际上反映高阶项及漂移项对瞬时相位的贡献；ΔPhmax为ΔPh的幅值最大值。

考虑到不同垂跨比下悬索响应周期不一致，为更直观比较f改变对Ph的影响，通过周期变换(纵坐标不变)，消除因悬索固有频率差异而导致的瞬时相位差，将各悬索的Ph时程变化曲线都统一为f=0.008 5的周期，如图5所示。

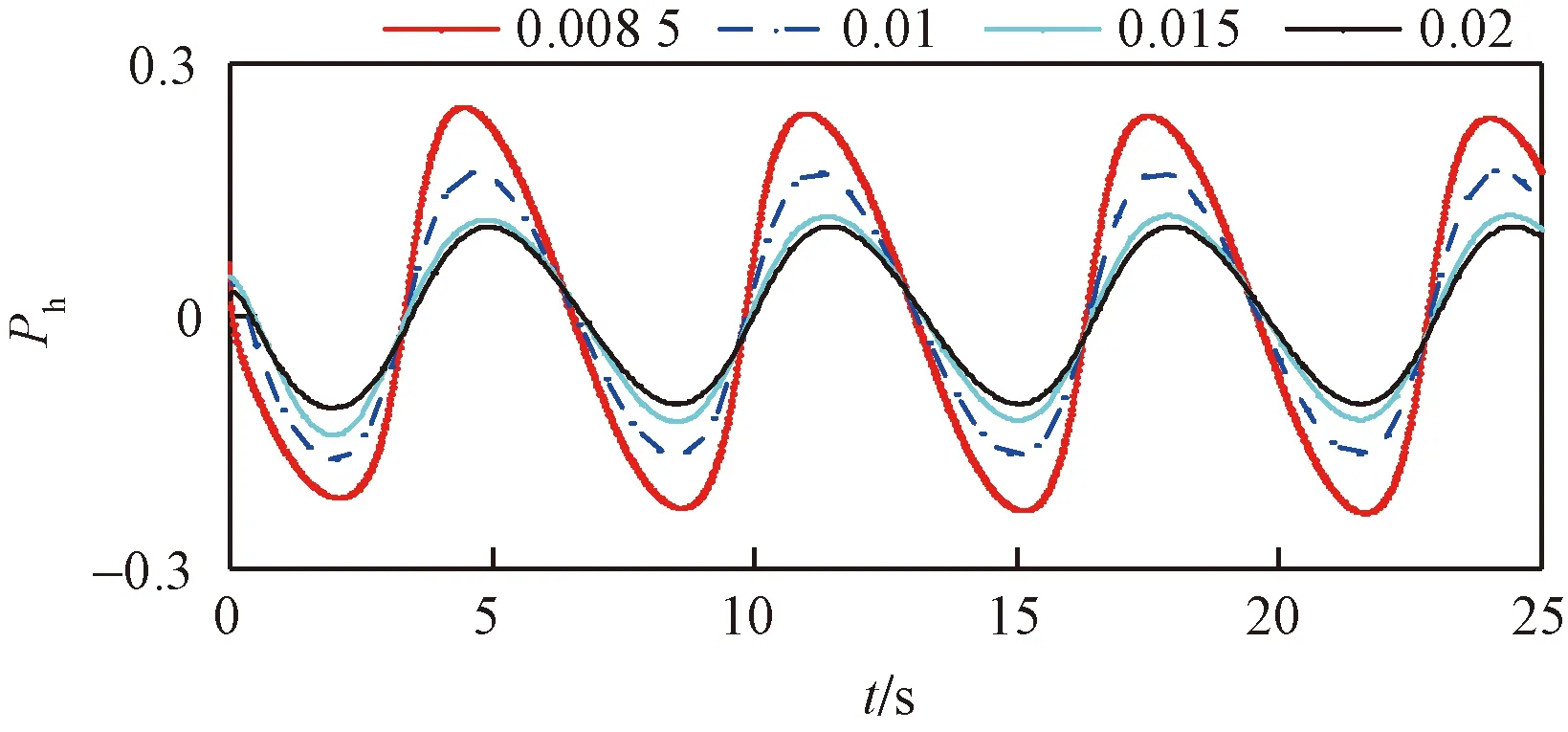
图5 周期变换过后的瞬时相位差时程曲线(σ=-0.5)Fig.5 Time history of transient phase difference after periodic transformation (σ=-0.5)

对比各悬索，发现Phmax随着f增大逐渐减小，但f从0.008 5变为0.01时，Phmax的变化值显然比从0.015变至0.02大，说明高阶项和漂移项对响应瞬时相位的影响大小与悬索参数取值范围有关。同时两者不仅对Phmax的数值大小有影响，当f为0.008 5和0.010的时候，它还使得Phmax出现的时机提前，对于同一个周期而言，从Phmax减少到-Phmax需要的时间长于从-Phmax增加到Phmax的时间，而当f为0.015和0.020时，该现象并不明显，因此图4中响应与激励的瞬时相位差在同一个周期内会出现两个时长不等递减区间的原因为高阶项和漂移项的影响。

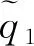
图6 高阶项和漂移项对响应瞬时相位的影响(σ=-0.5)Fig.6 Influence of higher-order term and drift term on transient phase of response (σ=-0.5)

整体而言，对比不同垂跨比悬索响应及线性项的复平面投影曲线发现，两者有很大不同，因漂移项的影响，各响应投影曲线明显整体往一二象限平移，且随着f的减小平移的趋势变得越大。具体而言，当f=0.008 5时，其响应投影曲线并非圆形，应是高阶项对其的影响，但不明显。在起点b与1/2周期处Ph为0，在c点时Ph有最大值Phmax，在d点Ph有最小值-Phmax，且c点与d点之间的时间间隔明显长于d点与b点之间，与图2中响应时程曲线“上宽下窄”特征相吻合，表明当垂跨比较小时，高阶项会引起Phmax出现的时机提前，导致响应与激励的瞬时相位差在同一个周期内会出现两个时长不等递减区间。由此，表明漂移项对Phmax数值大小起主导作用，而高阶项的影响则较小。

绘制漂移项随f变化曲线，如图6(b) 所示。由图6(b)可知，当f为0.008时，漂移项有最大值0.046，f从0.008 5增长到0.010，漂移项迅速减小到0.004，而在0.010到0.02范围内，漂移项的数值缓慢减小。结合图6(a)及图6(b)分析，表明各悬索垂跨比的不同主要通过改变其漂移项的大小来影响其瞬时相位。

2.3 参数分析

为进一步研究Phmax、垂跨比及调谐参数三者之间的关系，f取值[0.008,0.024]，变化步长为0.001，调谐参数取值[-0.6,0]，变化步长为0.02，绘制f-σ-Phmax曲面图在f-σ平面、f-Phmax平面及σ-Phmax平面的投影曲线如图7所示。

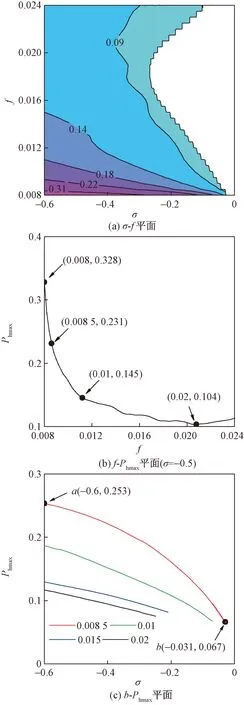
图7 f-σ-Phmax曲面Fig.7 f-σ-Phmax surface

图7(a)为f-σ等高线图。当垂跨比为[0.008,0.012]时等高线更密集，且等高线数值的变化更大，说明该范围内Phmax对垂跨比及激励频率变化更加敏感。

图7(b)为σ=-0.5时f-Phmax平面投影曲线。表明悬索f变化对Phmax影响较大，Phmax在f=0.008时有最大值0.328，当0.008

图7(c)为4种垂跨比下悬索的σ-Phmax曲线图，可以发现调谐参数的改变同样会对Phmax产生较大的影响。Phmax整体均随着σ增大而减小，即响应中高阶项和漂移项成分对响应瞬时相位的影响随着调谐参数的增大而逐渐减小。对比各悬索发现，垂跨比越小，调谐参数对Phmax的影响越明显，当f=0.008 5时，Phmax最大值能达到0.253，同时随着σ的变化，Phmax减小的速率逐渐变快，而其余3个垂跨比下悬索的Phmax与σ基本呈负相关。因此，对于垂跨比较小的悬索而言，高阶项和漂移项对响应相位的影响随调谐参数的变化会变得复杂，其变化速率逐渐加快，而对于垂跨比较大的悬索，调谐参数与其基本呈负相关。

3 结论

(1)高阶项及漂移项成分对其瞬时相位具有较大影响，若不计两者的影响瞬时相位差的误差，甚至能达到0.328π，其中，漂移项起主导作用。

(2)响应与线性项的最大相位差与垂跨比成反比，当垂跨比较小时，垂跨比的微小改变会引起该相位差最大值的巨大变化。

(3)响应与线性项的最大相位差整体随调谐参数增大而逐渐减小，且对于垂跨比较小的悬索而言，调谐参数的变化使该相位差变化速率逐渐加快。