卫星在轨抗辐照总剂量数据拟合及其应用*

王君峰，宋长旭，张缓缓，张学娇

(中国空间技术研究院西安分院，西安 710000)

0 引言

带电粒子辐射是空间环境要素中对航天器具有较大影响的重要因素之一。对卫星影响较大的空间辐射效应主要有：总剂量效应、单粒子效应、内带电效应、位移效应等。空间辐射效应严重时导致航天器电子设备工作异常，甚至报废[1-3]。因此对航天电子设备进行抗辐照分析加固设计，对提高其可靠性，保证在轨正常运行具有重要的意义。在工程实践中，针对不同的效应采取不同的抗辐照加固措施。例如总剂量效应采用增加屏蔽厚度的方法[4-7]，单粒子反转采用软件定时刷新的方法等。文章主要探讨总剂量效应的分析计算。

辐照总剂量分析计算的输入一般为一维实心球模型，如图1所示，其含义为：对于卫星轨道上放置的具有一定质量的实心屏蔽球，其球心位置剂量点所吸收的空间辐射剂量与球半径(等效铝厚度)间的关系[8]。

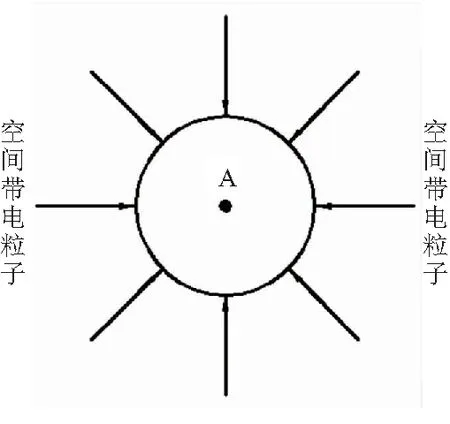
图1 一维实心球模型

由一维实心球模型延伸可得空间某点的三维抗辐照分析的基本思想是：通过计算各屏蔽厚度达到该点的剂量，然后进行叠加，得到该点的总剂量。由于航天电子设备基本上为长方体空间，进一步可延伸为六面法[9]。即对于长方体空间内的剂量点，如图2所示，其总剂量为6个方向的剂量叠加：

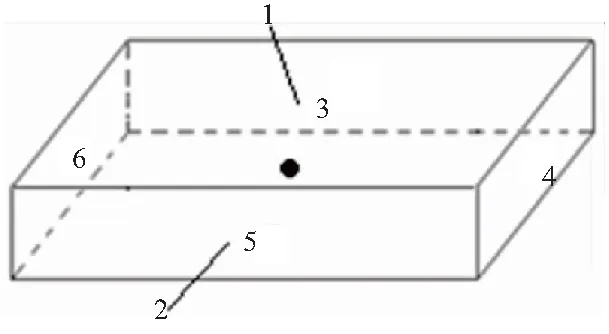
图2 长方体空间内的剂量点

工程实践中将一维实心球模型以数据表形式给出，供各个电子设备抗辐照加固设计参考。表1为某型号卫星在轨抗辐照总剂量剂量数据表。

总剂量计算校核时，根据实际屏蔽厚度查表进行计算。对于表中不存在的数据一般通过临近点或者取中值估算[10]。缺点是估算精度低，数据梯度变化较大处误差较大。特别地遇到大于表中屏蔽厚度的情况则无法计算,文章基于该问题进行了在轨剂量数据的拟合。

表1 某型号卫星在轨抗辐照总剂量

1 分段二次函数拟合

基于辐照总剂量一维实心球模型的特点，剂量深度曲线应该是光滑连续且递减的曲线。文章采用分段二次函数的方法进行曲线拟合，确保了数据表中已有数据无偏差，同时兼顾了曲线的平滑性。该方法用屏蔽厚度所在位置的前一个数据点和后两个数据点拟合二次函数来表征该数据点前后数据点之间区域的抗辐照总剂量数据。若用(xn,yn)表示在轨剂量深度表中第n行的数据，表中数据共k行，则采用分段二次函数拟合的在轨总剂量曲线f(x)如式(1)所示：

(1)

式中x表示屏蔽厚度，xn表示剂量深度表中第n行的屏蔽厚度，yn表示xn对应的总剂量。gn(x)表示由(xn,yn)，(xn+1,yn+1)，(xn+2,yn+2)三点确定的二次函数曲线。

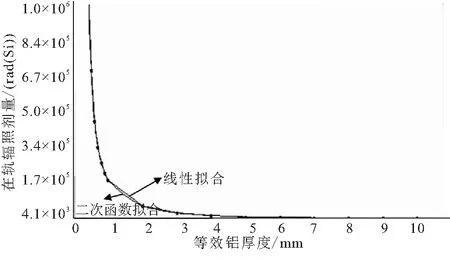
图3 分段线性拟合与分段二次函数拟合对比

图3为某型号数据采用分段二次函数拟合(图中下方曲线)与分段线性拟合(图中上方曲线)的效果对比。两者都能涵盖所有已知数据点，但分段二次函数拟合在等效铝屏蔽厚度变化剧烈的区域，如图中(1，2)之间区域更接近真实情况。

2 指数函数拟合

卫星在轨抗辐照总剂量数据表一般只给出大多数元器件有风险的数据点，工程实践中对于某些辐照总剂量特别敏感的元器件会遇到超出表中数据点的情况。例如MSK器件，一般要求辐照总剂量低于5 Krad(Si)，而表1中数据最小剂量为5.87 Krad(Si)，已无法对抗辐照校核加固提供依据。盲目通过加厚屏蔽件厚度未必能达到降低辐照剂量的目的。针对该情况，文章通过分析大量型号数据，提出了指数拟合的方法用于未知数据的预测。

(a)数据1总剂量取对数后散点图 (b)数据2总剂量取对数后散点图

(c)数据3总剂量取对数后散点图 (d)数据4总剂量取对数后散点图

从图4可以看出，取对数后数据点(xn，yn)的分布几乎在一条直线上。采用最小二乘法进行线性拟合，线性相关系数R2分别为0.966，0.938，0.939，0.975，表明两者具有很高的线性关系[11]。将(xn，yn)的线性关系记为y′=ax+b，则后半段辐照总剂量深度曲线可写成y=10ax+b。对于屏蔽厚度超出表中数据范围的情况，可以用该拟合公式来计算。因而在轨总剂量曲线f(x)可以扩展如式(2)所示。

(2)

采用二次函数与指数函数相结合的数据拟合方法能够对卫星在轨辐照剂量数据进行较为完整的表达。涵盖了在轨辐照剂量表中的所有数据点，同时可以对超出表中范围的数据进行预测，对空间电子设备抗辐照加固设计提供了更精确的数据支撑。

3 工程应用

根据式(2)可以编写程序对空间电子设备抗辐照指标进行校核计算。具体算法为：

1)根据实际屏蔽厚度查在轨计量表，确定数据区域；

2)根据数据区域，利用式(2)结合前后数据点拟合二次函数；

3)将屏蔽厚度带入拟合的二次函数，计算辐照剂量。

指数拟合对于数据表之外辐照剂量的计算提供了数据支撑。例如针对表1中的数据，假如某芯片抗辐照指标为总剂量小于5 Krad(Si)。表1的数据最大屏蔽厚度对应的辐照剂量为5.87 Krad(Si)，5 Krad(Si)显然超出了数据范围，无法进一步计算需要的屏蔽厚度。利用式(2)的指数拟合方法，取表中后10个数据点，取对数后拟合的直线如图2左上角图。y′=-0.021 5 +4.163 7，因而辐照剂量公式为：y=10-0.021 5x+4.163 7。利用该公式计算得到的数据与实际数据对比如表2所示。可以看出两者相对误差在4%以内，拟合效果较好，能够满足工程计算需要[12]。将屏蔽厚度21 mm带入公式，可得辐照剂量为4.905 Krad(Si)，因而要满足该芯片5 Krad(Si)的指标，需要将屏蔽厚度增加到21 mm以上。

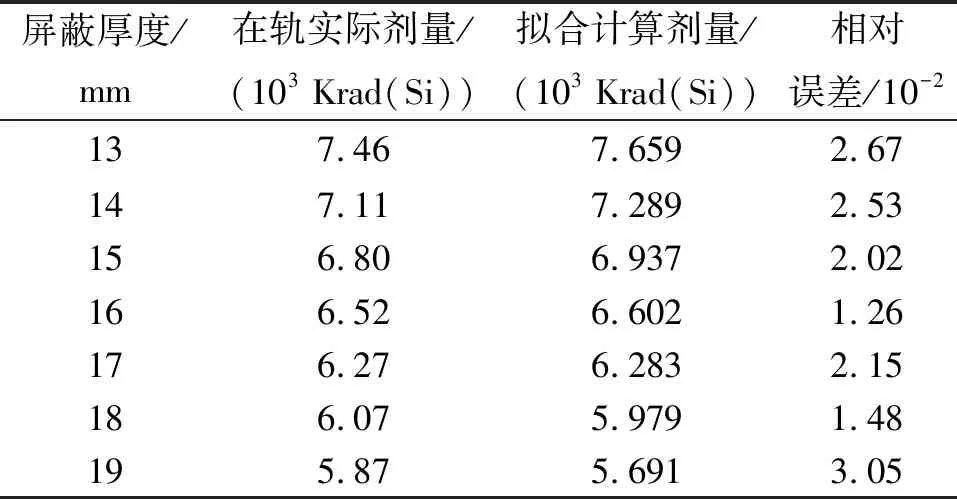
表2 指数拟合数据与实际数据对比

4 结论

文章从工程实际的大量数据出发，提出了分段二次函数拟合与指数函数拟合相结合的方法，对空间在轨辐照剂量表数据拟合。该方法解决了在轨辐照剂量表中数据点过少导致的梯度变化剧烈处计算偏差较大，以及数据表范围之外数据无法计算的问题。拟合精度高，能够满足工程计算的需要。该方法已用于多个在轨型号的抗辐照校核计算，对于提高空间电子设备抗辐照计算校核的精度，提高设备的可靠性具有积极意义。