同时次梯度投影算法求解分裂可行性线性收敛性研究①
2021-11-10王晓霞
王晓霞
(齐齐哈尔大学理学院,黑龙江 齐齐哈尔 161000)
0 引 言
有限维欧式空间中的分裂可行性问题是一种实际工程中抽象出来的一种应用广泛的数学模型,在信号处理、图像重建和医学模拟等方面都发挥着重要的作用,备受相关学者关注[1]。多集分裂可行性问题(MSSFP)是分裂可行性问题的一个重要推广,其本质与分裂可行性问题的本质相同,均为一种优化问题。目前,针对多集分裂可行性问题,许多学者提出了不同的求解算法,均取得一定成效,但这些算法的收敛性不够优秀,收敛速度也无法得到保证[2]。使用动态步长的方法来对传统的梯度投影算法进行优化,利用带有动态步长的同时次梯度投影算法(SSPA)求解希尔伯特空间中的多集分裂可行性问题,并对该算法的收敛性与收敛速度进行研究。研究结果表明,SSPA算法拥有优秀的收敛性和较快的收敛速度,能够高效求解多集分裂可行性问题,具有较高的实用价值。
1 SSPA算法对多集分裂可行性问题的求解
1.1 希尔伯特空间中MSSFP问题的预备知识
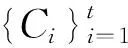

(1)
公式(1)中,x为H中的一个点。多集分裂可行性问题的解集能够表示为公式(2)。
S:=C∩A-1Q={x∈C:Ax∈Q}
(2)
公式(2)中,S表示多集分裂可行性问题的解集。当多集分裂可行性问题的解集连续时,则表示S为非空闭凸集合,则有公式(3)。
(3)
‖xn-x*‖≤ωσn
(4)
公式(4)中,xn为希尔伯特空间H中的一个数列,σ为收敛率,且取值范围为0~1,x*表示序列的线性收敛极限ω>0,n为一个正整数。多集分裂可行性问题为有界线性正则,其具体描述为:若对于任意r>0都有一个对应常数τr>0,使任意一个x∈C∩rB都有如公式(5)所示。
τrds(x)≤dQ(Ax)
(5)
公式(5)中,ds(x)表示点x到集合S的距离,dQ(Ax)表示点x到集合Q的距离。设G:H→H2为一个有界线性算子,则用kerG表示G的核,则有公式(6)。
kerG={y∈H:Gy=0}
(6)
kerG的正交补则表示为kerG⊥,其表达式如公式(7)所示。
kerG⊥={x∈H:〈y,x〉=0,∀y∈kerG}
(7)
kerG与kerG⊥都是H的闭子集。设G:H→H2为一个有界线性算子,则G为单射且有闭值域,且G为下方有界,那么则有一个数v使得所有的w∈H都有公式(8)成立。
‖Gw‖≥v‖w‖
(8)
公式(8)中,v是一个正整数。设{S′,kerG}为有界线性正则,且G有闭值域,则多集分裂可行性问题满足有界线性正则的条件。结合上述公式与内容,即可证明多集分裂可行性问题是有界线性正则的。
1.2 带有动态步长的同时次梯度投影算法
求解多集分裂可行性问题的核心思想即将待求解的问题转化为最小化问题来进行求解。对于多集分裂可行性问题,一般采用投影梯度法来进行求解[4],投影梯度法的迭代形式如公式(9)所示。
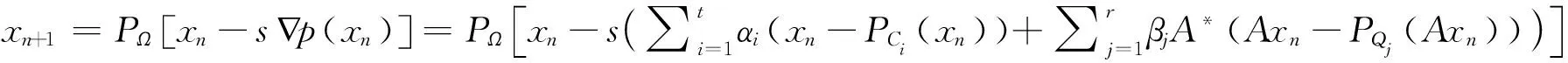
(9)
公式(9)中,Ω是一个辅助的简单闭凸集合,且满足Ω⊂RN,p(x)是一个函数,用来表示任意点x到所有集合的距离。投影梯度算法的计算量大,操作难度较高,因此有学者基于投影梯度算法,提出一种易于执行、操作简便的,利用正交投影到半空间来对多集分裂可行性问题进行求解的同步次梯度投影算法[5-6],如公式(10)所示。
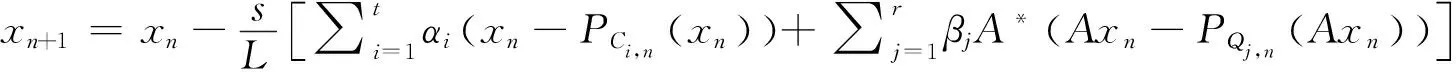
(10)
公式(10)中,s∈(0,2),ρ(A*A)是A*A的谱半径,αi,βi均大于0。同步次梯度投影算法解决了投影梯度算法计算量大,执行不便的缺点,但同步次梯度投影算法的步长为固定步长,因此算法的收敛速率较慢,求解多集分裂可行性问题的效率较低[7]。针对这一问题,有学者基于求解凸可行性问题的外推法提出一种同时次梯度投影算法,用以求解多集分裂可行性问题,该算法利用算法在迭代过程中的外推因子来提高收敛速率。为了进一步提高算法的收敛性,研究提出一种带有动态步长的同时次梯度投影算法。设有两个集合Ci,Qj,其表达式如公式(11)。
(11)
公式(11)中,ci:H1→R与qi:H2→R都是凸函数。假设ci与qj分别在H1与H2上均为次可微,且∂ci和∂qj在有界集上有界,根据次梯度的定义可以得到公式(12)。
(12)
公式(12)中,Ci,n为一个半空间,包含Ci,Qj,n为一个半空间,包含Qj。则有公式(13)。
(13)
利用正交投影定理,即能求解出点Ci,n到点Qj,n之间的距离,大大降低了计算量。多集分裂可行性问题的逼近函数如公式(14)所示。
(14)
公式(14)中,p(x,y)是多集分裂可行性问题的逼近函数,且对于任意的i与j,都有公式(15)。
(15)
根据公式(11)。即可得知函数p(x,y)具有是凸可微,并且具有梯度,如公式(16)。
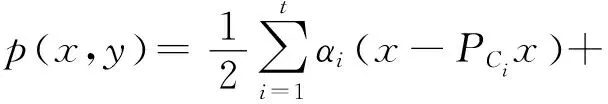
(16)
基于公式(16),提出一种新的迭代算法来求解多集分裂可行性问题,如公式(17)。
xn+1=xn-
(17)
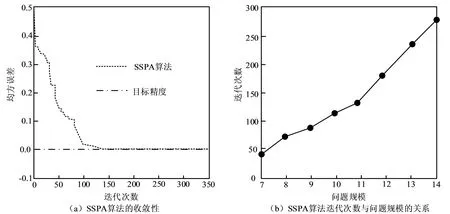
公式(17)中,0 (18) 根据公式(17),即可得到求解多集分裂可行性问题的SSPA算法。对于公式(11)中的每一个初始点x0∈C,序列{xn+1}由公式(19)生成。 xn+1=xn- (19) 公式(19)在任意迭代次数n处应满足收敛性,如公式(20)。 (20) 满足公式(20)的同时,还应该满足公式(21)。 (21) 在公式(21)中,αi应满足公式(22)。 (22) SSPA算法能够高效求解多集分裂可行性问题。 为验证SSPA算法是否具有收敛性利用Wolfram Mathematica软件对算法的性能进行测试,测试结果如图1所示。 图1 SSPA算法的收敛性能 从图1(a)能够看出,随着迭代次数的增加,SSPA算法的均方误差在减少,精度在上升,说明算法具有收敛性。SSPA算法在迭代171次时,误差精度达到0.001,这说明 SSPA算法具有良好的收敛性。由图1(b)能够看出,处理的问题规模越大,算法需要的迭代次数越多。在处理问题规模为7时,SSPA需要迭代48次,在处理问题规模为11时,算法需要迭代146次,当处理问题规模为14时,算法需要迭代270次,与实际情况相符合,说明算法具有实用性。 在求解多集分裂可行性问题时,算法在迭代次数、计算次数以及运算时间等方面的性能会对求解过程的速度、效率、以及求解结果的精度造成极大的影响。为验证SSPA算法能否满足实际需求,将同时次梯度投影算法记为算法2,投影梯度算法记为算法3,测试并对比三种算法的性能,P为当前算法在t倍最佳时间内优于其他算法的几率,测试结果如图2所示。 图2 SSPA算法的各项性能对比 从图2中能够看出,SSPA算法在迭代次数、计算次数以及运算时间等方面的性能的数值表现均优于同时次梯度投影算法和投影梯度算法。从图2(a)中可以看出,SSPA算法求解全部问题的迭代次数会明显低于另外两种算法;在一定时间内,SSPA算法以最少的迭代次数能够对84.9%的测试问题进行成功求解;同时次梯度投影算法以最少的迭代次数能够对68.2%的测试问题进行成功求解,比SSPA算法少16.7%;投影梯度算法以最少的迭代次数能够对58%的测试问题进行成功求解,比SSPA算法少26.9%。从图2(b)能够看出,SSPA算法求解全部问题的计算次数明显低于另外两种算法,在25倍最佳时间内,SSPA算法能够以最少的计算次数求解98.7%的问题,比同时次梯度投影算法的93.6%高5.1%;比投影梯度算法的89%高9.7%。从图2(c)能够看出,改进三项共轭梯度算法求解全部问题的运算时间远少于另外两种算法,在一定时间内,SSPA算法能以最少的运算时间求解74.8%的测试问题。 为验证SSPA算法的收敛速度优于同时次梯度投影算法和投影梯度算法,将同时次梯度投影算法记为算法2,投影梯度算法记为算法3,以同样的多集分裂可行性问题测试三种算法的收敛速度,测试结果如图3所示。 图3 SSPA算法的收敛速度 从图3中能够看出,SSPA算法要使精度达到0.001需要迭代124次;同时次梯度投影算法要达到0.001的精度需要迭代261次,比SSPA算法多137次;而投影梯度算法迭代350次之后也未能达到0.001的精度。以上结果说明,SSPA算法的迭代速度更快,更适合用来求解多集分裂可行性问题。 目前针对多集分裂可行性问题的求解算法的收敛性不够优秀,收敛速度较慢。利用带有动态步长的同时次梯度投影算法多集分裂可行性问题,并对算法的性能进行验证。结果表明,随着迭代次数的增加,SSPA算法的精度在上升,说明算法具有收敛性;SSPA算法以最少的迭代次数能够对84.9%的测试问题进行成功求解,比算法2多16.7%,比算法3多26.9%;在25倍最佳时间内,SSPA算法能够以最少的计算次数求解98.7%的问题,比算法2多5.1%,比算法3多9.7%;在一定时间内,SSPA算法能以最少的运算时间求解74.8%的测试问题;,SSPA算法要使精度达到0.001需要迭代124次,比算法2少137次,算法3在350次迭代后未能达到目标精度。以上结果说明,SSPA算法是一种收敛性优秀,收敛速度快的算法,有较高的实用价值。接下来需要尝试将SSPA算法与实际问题相联系,提高其实用性。2 对SSPA算法求解MSSFP问题的性能研究
2.1 SSPA算法的收敛性研究
2.2 对SSPA算法的各项性能研究

2.3 SSPA算法的收敛速度研究

3 结 语
