水轮机非线性密封力近似解耦方法
2021-11-10郭志成邹屹东
于 磊, 曾 云, 钱 晶, 郭志成, 王 伟, 邹屹东
(昆明理工大学冶金与能源工程学院, 昆明 650098)
水轮机发电机组轴系振动是影响机组运行安全的主要因素之一, 而水轮机密封结构复杂、间隙小, 止漏装置前后压力差较大, 易在间隙中产生压力脉动形成密封力,因此水轮机密封力对轴系振动的影响引起了广泛关注.孔达等[1]对比Thomas-Alford模型、Black-Childs模型、Muszynska模型在非线性密封力研究中的应用, 验证了Muszynska模型的合理性; Zhang等[2]利用Muszynska模型描述密封间隙产生的非线性流体力, 并采用摄动法对密封腔产生的流体力进行数值模拟; Wu等[3]建立了一个在不平衡磁拉力和Muszynska非线性密封力作用下的简化轴系模型,研究了混流式水轮机密封系统的非线性稳定性; He等[4]基于双控制容积模型和转子的运动方程, 提出了一种描述转子密封系统密封力的非线性模型.也有学者通过CFD软件研究转子密封, Zhang等[5]基于非线性Muszynska模型, 通过CFD直接瞬态模拟研究大静偏心和大动扰动下的环形密封; Griebel[6]结合试验数据与两种不同CFD模型的计算结果, 研究了叶片密封的泄漏性能; Woo等[7]通过CFD分析了螺旋槽密封的泄漏特性,提出了改进螺旋槽密封形状以减少泄漏的建议.
密封转子系统的研究主要围绕临界失稳转速展开.从转子动力学来看, 轴系振动采用集中参数模型时,引入非线性外力,导致振动模型中演变出阻尼和刚度耦合.若将振动系统解耦为单自由度问题,则诸多经典振动力学理论均可用于系统振动特性的研究;因此,解耦是研究非线性振动的关键.目前,强迫解耦法、Kelly法、近似实空间解耦法[8]已被应用于振动微分方程解耦中.本文基于强迫解耦法, 拟提出一种用于非线性密封力影响下水轮机振动模型近似解耦方法, 通过Runge-Kutta法仿真验证该方法的可行性, 并分析近似解耦后密封半径与密封长度对转轮振幅的影响.
1 轴系暂态模型
水力机组轴系结构如图1所示.B1,B2和B3分别为上导轴承、下导轴承和水导轴承的几何形心,O1和O2为转子和转轮的几何形心, 其中|B1B2|=a, |B1O1|=|O1B2|=a/2, |B2B3|=b, |B3O2|=c, 主轴长度L=a+b+c.根据文献[9], 转子径向位移为r1, 转轮径向位移为r2, 上导轴承径向位移r3=[2(a+b+c)r1-ar2]/(a+2b+2c), 下导轴承径向位移r4=[2(b+c)r1+ar2]/(a+2b+c), 水导轴承径向位移r5=[2cr1+(a+2b)r2]/(a+2b+2c).

图1 水轮发电机组轴系结构Fig.1 Shafting structure of hydro generator set
发电机转子和水轮机转轮振动微分方程分别为
(1)
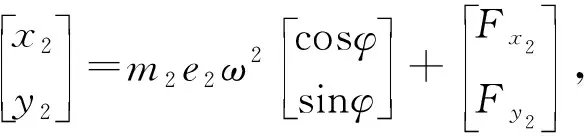
(2)
式中m1和m2分别为发电机转子和水轮机转轮的质量;K11和K22分别为轴承刚度折算到发电机转子和水轮机转轮的等效刚度,K12为耦合刚度, 具体计算过程参考文献[10];c1和c2分别为作用在转子和转轮上的阻尼系数;e1和e2分别为转子和转轮的偏心距;r(ω)为转子振动幅值与转轮振动幅值的比值;Fx1和Fy1分别为转子所受附加外力在x和y方向的分量,Fx2和Fy2分别为转轮所受附加外力在x和y方向的分量;ω为机组转速;φ为机组转过的角度; 转子形心坐标为(x1,y1), 转轮形心坐标为(x2,y2).
1.1 Muszynska非线性密封力模型
Muszynska认为流体作用力与流体一起, 以平均角速度τω旋转, Muszynska非线性密封力模型表达式为

(3)
式中Fx3和Fy3分别为作用于水轮机转轮上的密封力在x和y方向上的分力,K为密封力的当量刚度,D为当量阻尼,mf为当量质量,τ为流体周向平均速率比.上述参数具体计算过程参考文献[2].
1.2 水轮机非线性密封力模型
图2为水轮机密封结构示意图.由图2(a)可知, 水轮机密封结构设置水封装置, 其中上密封防止水流从间隙进入顶盖,下密封避免水流泄露造成水力损失;密封间隙越大, 漏水量越大,水轮机转轮因质量偏心或机械安装偏差等客观因素影响,转轮周围的密封间隙会变得不均匀.结合图2(b)可知,n处间隙大于m处, 水流通过上密封进入空腔,空腔会在nm方向产生随转轮转动而变化的平衡水流,从而形成流体力矩, 使机组振动更加剧烈.因此, 建立振动模型时,可将非线性密封力折算为作用于水轮机转轮的附加外力.
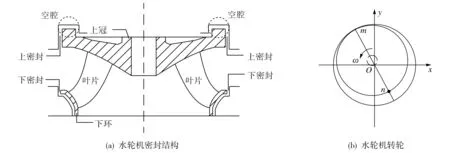
图2 水轮机密封结构示意图Fig.2 Simplified structure of turbine seal
结合水轮机振动微分方程与非线性密封力模型,得到非线性密封力影响下的水轮机振动微分方程
(4)
式中M为转轮质量与密封力当量质量之和, 表示水轮机非线性密封力模型的等效质量, 即M=m2+mf.式(4)的简化形式为
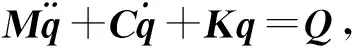
(5)
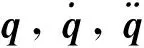
(6)
2 振动微分方程求解
关于水轮机非线性密封力振动微分方程的求解,若能采用振型叠加法中的矩阵正交化解耦,即可直接得到振动解析式.考虑到水轮机非线性密封力模型中的阻尼矩阵和刚度矩阵均为非对角阵,无法正交化,故选用强迫解耦法进行初步近似解耦.强迫解耦法忽略耦合项,将多自由度方程解耦为多个单自由度方程,故式(6)强迫解耦为
(7)
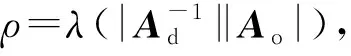
密封力当量阻尼D与流体周向平均速率比τ是影响转轮密封系统稳定的主要参数[1],而强迫解耦所忽略的耦合项CA和KA包含这两个参数,为进一步减小强迫解耦造成的振幅误差,整合式(6)中被忽略的元素Cr和Kr,得到
(8)
式中Cr取值为0,CA或-CA;Kr取值为0,KA或-KA.
3 仿真分析
以某电站实际水轮发电机组为例, 水轮机主要参数: 转轮质量m=3×105kg; 转轮半径R=1.708 m; 稳态运行时的角速度ω=13 rad·s-1; 上导轴承、下导轴承、水导轴承的刚度分别为K1=2.0×108N·m-1,K2=2.0×108N·m-1,K3=3.5×108N·m-1; 轴的几何尺寸分别为a=4.0 m,b=3.0 m,c=1.2 m.水轮发电机组在稳定工况下运行, 不考虑发电机部分, 取密封压降ΔP=5×105Pa, 进口损失系数ξ=1.5, 轴面流速v=3.537 m·s-1, 密封长度l=0.43 m, 密封半径r=2.925 m, 密封间隙c0=2.5 mm, 流体动力黏性系数γ=1.3×10-3Pa·s, 转轮阻尼De=5.0×104N·m-1.将上述数据代入式(4), 得到阻尼矩阵的对角占优指数为0.042 41, 刚度矩阵的对角占优指数为0.002 732, 则近似解耦的误差较小, 可进行近似解耦.
本文选用8种近似解耦方案, 仿真计算后的振幅误差如表1所示.由表1可知,方案5近似解耦造成的振幅误差相对较小.

表1 近似解耦方案表
利用MATLAB软件编程, 实现Runge-Kutta方法对未解耦、强迫解耦及近似解耦方案5下振动微分方程的仿真计算.图3~6为稳定运行下水轮机转轮振幅变化和形心轨迹.由图3~6可知,机组稳定运行时, 强迫解耦和近似解耦后与未解耦的振动曲线吻合, 三者转轮形心轨迹几乎重合,解耦误差主要体现在振幅上, 未解耦时振幅为1.087×10-4mm, 强迫解耦后振幅为1.092×10-4mm, 近似解耦后振幅为1.087 1×10-4mm, 近似解耦下的振幅误差较小.

图3 水轮机转轮x方向振幅Fig.3 x-Direction amplitude of turbine runner
当耦合项参数τ和mf因密封故障而变大时, 不同解耦方法的仿真结果如图7所示.由图7可知, 当耦合参数发生畸变时,强迫解耦的振幅误差变大,近似解耦拟合结果较好,振幅误差较小.
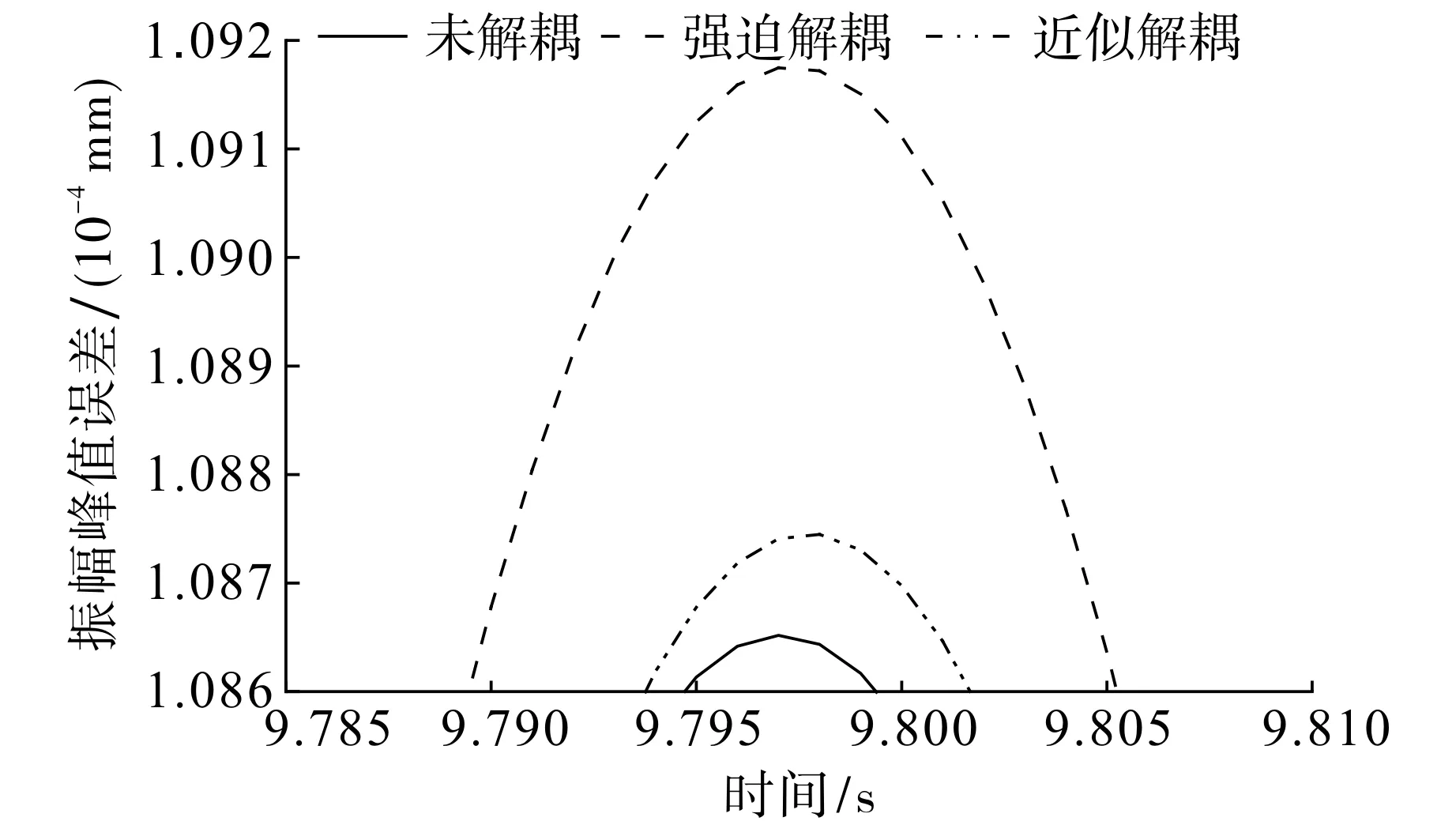
图4 水轮机转轮振幅峰值误差Fig.4 Amplitude peak error of turbine runner

图5 水轮机转轮稳态振幅Fig.5 Steady state amplitude of turbine runner
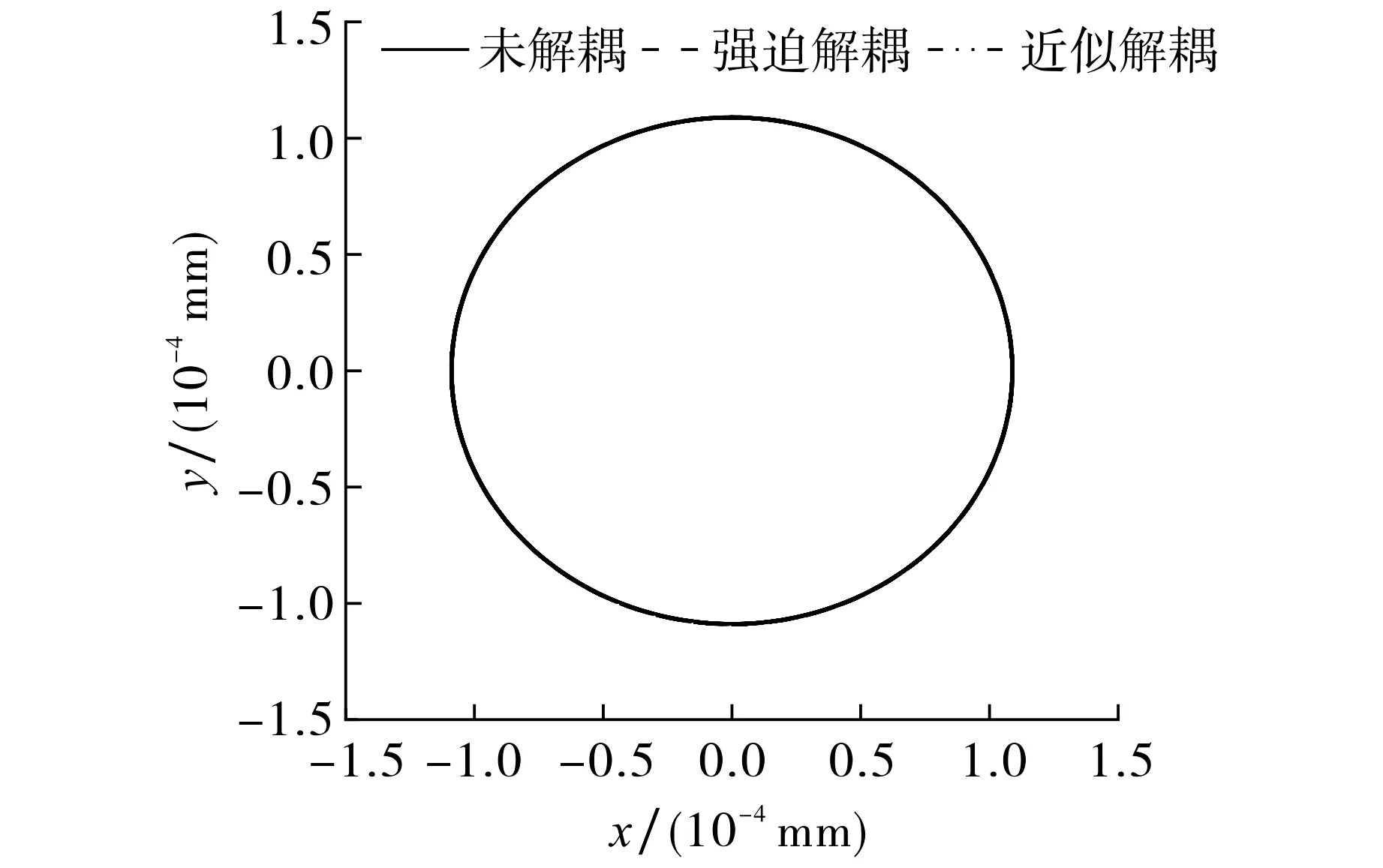
图6 水轮机转轮稳态形心轨迹Fig.6 Steady state centroid trajectory of turbine runner
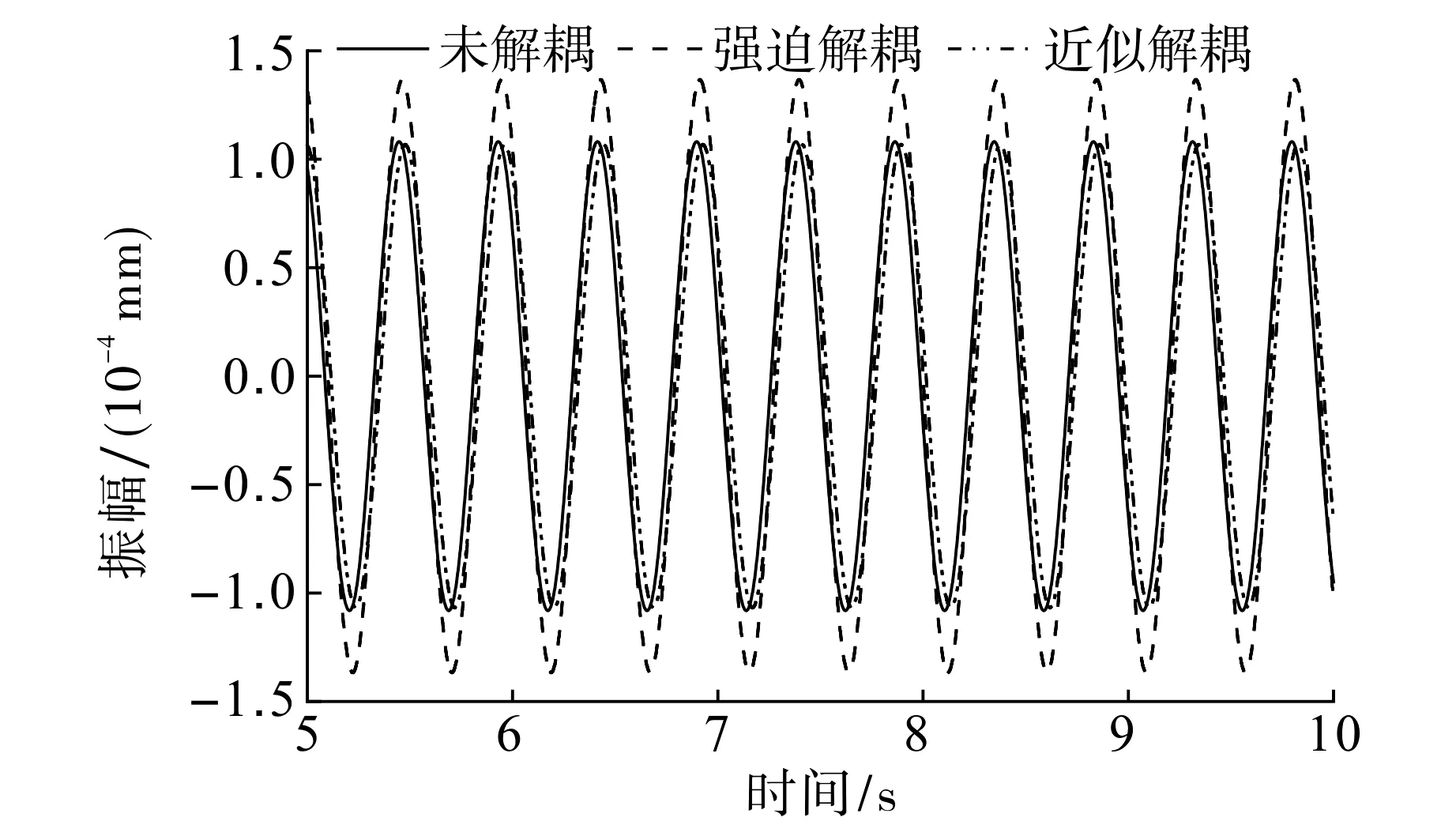
图7 耦合参数畸变后水轮机转轮x方向振幅Fig.7 x-Direction amplitude of turbine runner after coupling parameter distortion
进一步研究相同运行工况下近似解耦后的水轮机非线性密封力模型,得到密封半径和密封长度的变化对振幅的影响, 如图8所示.由图8可知, 当密封长度不变,密封半径在一定范围内变化时, 水轮机转轮振幅变化不明显;当密封半径不变,密封长度在一定范围内变化时,水轮机转轮振幅的变化较为明显,振幅随密封长度增加而逐渐增大;当密封半径与密封长度同时增加时, 水轮机转轮振幅变化更为显著,呈逐渐升高的趋势, 与实际情况相吻合.
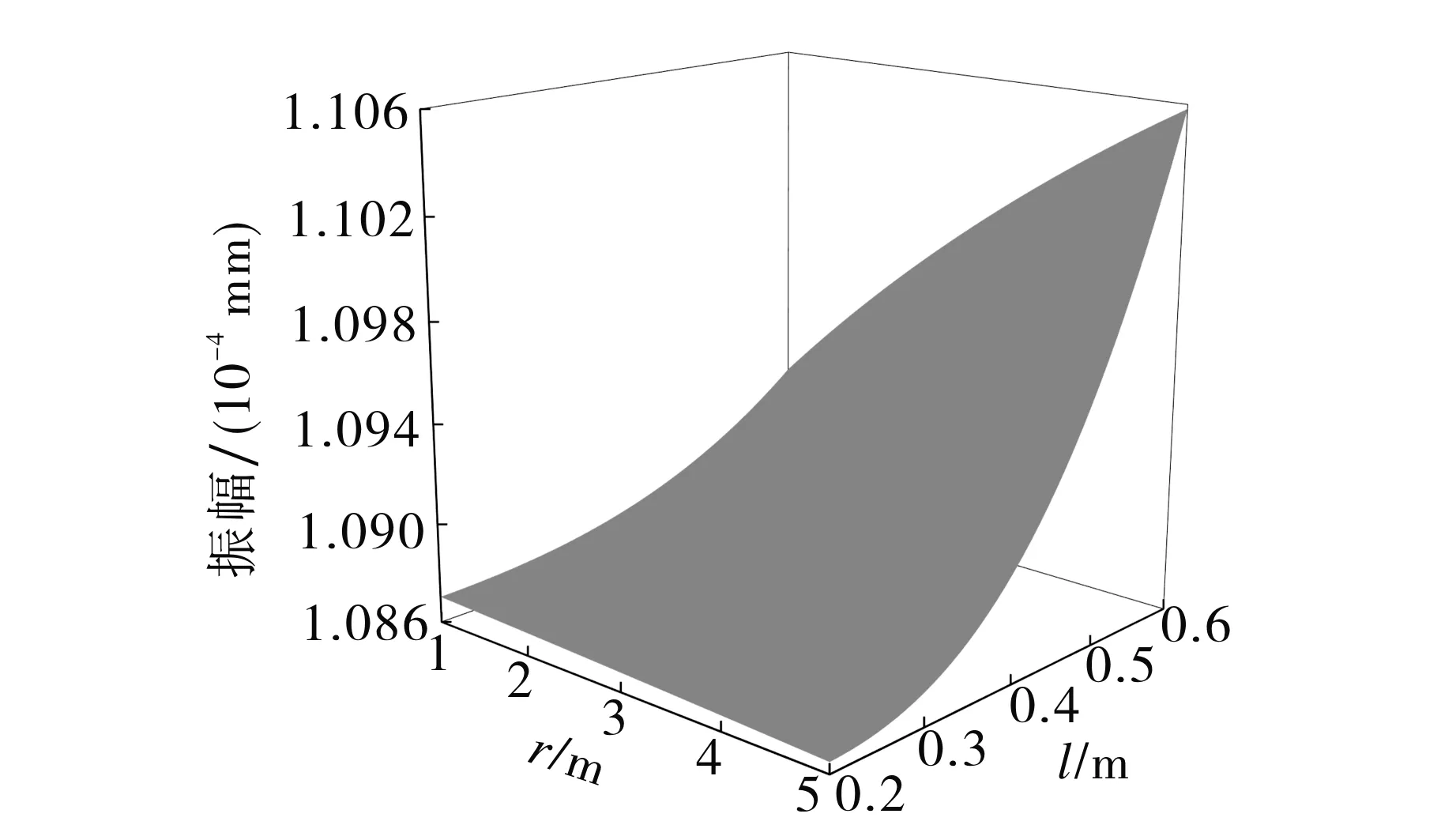
图8 密封半径与长度对振幅影响图Fig.8 Influence of seal radius and length on amplitude
4 结论
1) 本文提出的近似解耦方法在水轮机稳态运行及耦合项参数因密封故障而发生畸变时,对水轮机非线性密封力模型的拟合效果均较好.
2) 水轮机组运行时,密封长度对转轮振幅的影响较大,转轮振幅随密封长度与密封半径的增大而增大,密封设计时须合理选取密封长度与密封半径.
