混凝土梁破坏过程中声发射特性及ba值的变化

2021-11-10顾爱军王举国

扬州大学学报（自然科学版） 2021年3期

苏铭, 顾爱军, 王举国

(扬州大学水利科学与工程学院, 江苏扬州 225009)

混凝土作为一种广泛使用的建筑材料, 结构易受到载荷、化学腐蚀等因素作用产生严重的损伤,从而降低混凝土强度和稳定性．为了确保建筑物的长期、安全、稳定运行,必须对混凝土结构的损伤进行长期监测,同时需要在结构发生严重损伤或破坏前提供预警[1]．声发射作为一种经济、高效的无损检测技术,常用于评估土木工程设施(桥梁、水坝等)腐蚀、损伤程度[2], 能够监视材料从开始产生裂纹直至最终结构失效全过程产生的瞬态弹性波,从而反映出材料内部的裂纹产生、扩展[3-5]．为了评估材料的损伤程度, 须对采集到的声发射信号进行处理分析, 主要的方法有参数分析法和波形分析法两大类[6]．参数分析法中,b值最早由Gutenburg和Richter提出, 用作地震震级频度与活动水平的重要参数[7]．由于岩石破坏过程与自然地震极为相似,b值作为一个特殊的参数, 随着材料构造活动模式改变而发生相应变化[8], 众多学者已将b值用于评估岩石损伤状态．余洁等[9]通过单轴、三轴围压试验, 发现b值经历一段时间波动后产生较大幅度的下降; 刘希灵等[10]通过研究b值的变化, 发现灰岩在单轴压缩情况下从宏观裂纹的产生至最终失稳断裂所经历的时间比在劈裂情况下更长; 宋义敏等[11]则利用b值的变化表征岩石受剪力条件下各阶段裂纹尺度的大小; Liu等[12]发现岩石在冲击荷载作用下, 由于载荷持续时间短,微裂纹没有逐渐发展的时间,导致试验计算所得的b值整体偏小; Carpinteri等[13]将单一的综合参数b值用来表征混凝土材料三点弯曲试验中从产生宏观裂纹至最终断裂的过程, 认为b值的下降可代表材料出现局部损伤; Sagar等[14]发现在高加载速率下钢筋混凝土梁裂纹的快速发展会导致b值降低; Schumacher等[15]通过b值的变化来评估混凝土加载时的损伤、断裂情况, 认为宏观裂纹的产生常常是载荷变化造成的,b值在一定程度上可以反映外载荷的变化; 曹海[16]在研究不同聚乙烯醇(PVA)纤维掺量对混凝土强度的影响时, 利用b值实现了对试件损伤情况的分段, 并进行了对比评估; Farhidzadeh等[17]将b值的减小作为混凝土内部损伤累积的重要指标; 王宇[18]研究预应力钢筋混凝土梁三点弯曲分级加载试验过程中发现, 根据加载阶段分段计算的b值变化规律不明显且上下波动,认为其主要的原因是拟合的a、b两个值同时在变化,相互影响,并首次提出将a取平均值后固定,再对各个阶段进行拟合得到的ba值更能反映材料从微观裂纹向宏观裂纹转变的过程．但此方法在每级加载阶段仅计算得到1个ba值, 不能反映加载阶段、荷载保持阶段ba值的具体变化情况．

基于上述理论依据及ba值存在的缺陷, 本文拟通过钢筋混凝土梁四点弯曲分级加载试验、素混凝土梁四点弯曲连续加载试验, 将加载阶段细分为多段,进一步分析ba值变化规律,并提出一种可能预测结构损伤、失效的方法．

1 b值理论

1.1 G-R公式

在地震学中, Gutenburg和Richter于1941年建立了地震震级与频度之间的定量关系式G-R公式:

lgN=a-bM,

(1)

其中N为地震次数;M为地震震级;a,b为常数．从物理意义上,b值反映大地震与小地震之间的比例关系．b值增大代表着小地震的比例增大; 反之, 大地震的比例增大．根据研究与实验证明b值在地震波即将到达前或岩石处于临界破裂时会产生较为明显的波动, 所以可以将b值作为判断一定范围内地震活动的相关参数．同时, 由于声发射现象与地震的产生原理类似, G-R公式也被广泛应用于声发射分析．当声发射试验中采用速度传感器时, 式(1)变为[19]

lgNM=a-bAdB/20,

(2)

其中NM为声发射信号幅值超过M时的声发射事件数, 同时将声发射幅值转换为以分贝为单位的AdB．

1.2 b值与ba值的计算方法

在地震学中,b值的计算方法主要有最小二乘法与极大似然法．本文采用最小二乘法来计算, 具体计算公式为

(3)

其中Ai为第i档的中数; Δx为声发射事件分档间距．将某时间窗内的声发射数据根据幅值从29.5 dB开始, 以5 dB为步长进行分组．例如: 幅值大于29.5 dB且小于等于34.5 dB的声发射事件作为一组数据, 记为32 dB．以AdB/20为横坐标, logNM为纵坐标进行拟合, 可得到相应的a,b值．

2 试验方案

通过两组试验,即钢筋混凝土梁四点弯曲分级加载试验和素混凝土梁四点弯曲连续加载试验,进行声发射幅值、能量、振铃计数及声发射b值和ba值分析．

试验一: 使用四点弯曲的方法对一组150 mm×180 mm×1 500 mm的钢筋混凝土梁分级加载, 每级加载20 kN, 然后维持一段时间, 让裂纹充分发展, 再进行下一级加载, 直至梁破坏失效．采用325水泥, 混凝土强度为C30, 配合比为m(水)∶m(水泥)∶m(砂)∶m(碎石)=0.4∶1∶1.137∶2.652, 标准养护试件28 d以上, 混凝土实测抗压强度为34 MPa, 抗拉强度为2.7 MPa, 钢筋混凝土梁为适筋梁, 其配筋图如图1所示．

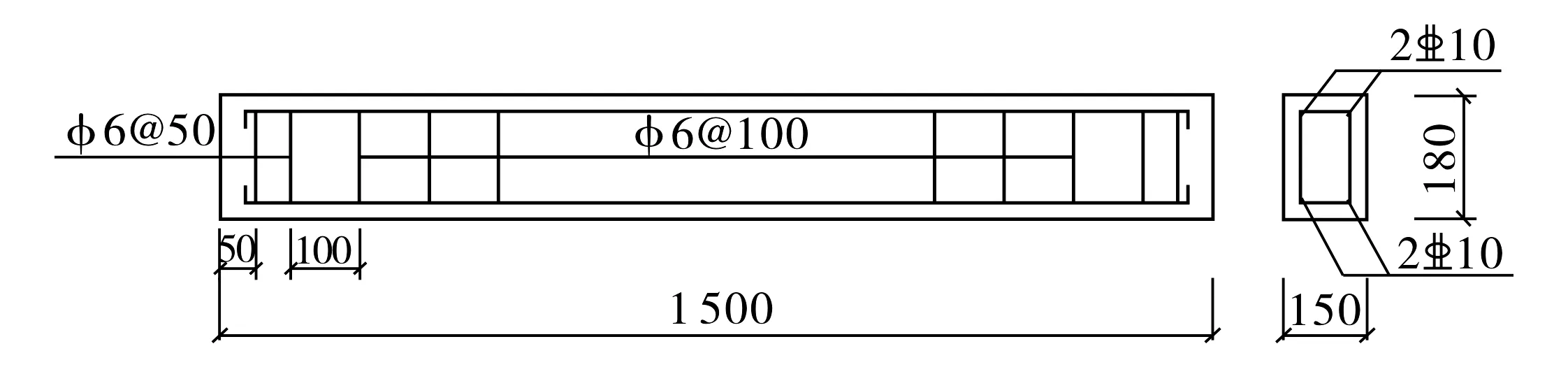
图1 钢筋混凝土梁配筋图(mm)Fig.1 Reinforcement of reinforced concrete beam

试验二: 使用四点弯曲的方法对一组150 mm×180 mm×1 500 mm素混凝土梁进行2 mm·min-1位移控制加载, 直至梁破坏失效．采用的混凝土与试验一相同．

采用WDI-AST型宽频声发射传感器(美国物理声学公司, 美国)对信号进行接收, 考虑到试验加载条件及环境,所以本次试验过程中声发射信号采集门槛设定为30 dB．加载系统为CSS-44 050型号的电子万能试验机(长春试验机研究所,长春), 并配以工字梁进行加载．将4个传感器分别布置在梁的上下表面, 为确保耦合,使用硅脂涂抹在两者接触面的位置, 并用有伸缩性的绑带加以固定, 如图2所示．

3 试验结果与分析

3.1 声发射常规参数分析

本文常规参数分析选择能量、振铃计数、幅值对钢筋混凝土梁和素混凝土梁四点弯曲试验过程中采集到的声发射信号进行分析．图3是钢筋混凝土梁的声发射主要参数随时间变化图．图3(a)显示,声发射事件大部分出现在分级加载的过程中, 且幅值超过8 dB的事件很少,主要集中于70 dB以下, 少量事件发生在保持荷载平稳期, 且幅值均小于前一级加载过程中的声发射幅值．图3(b)(c)显示能量释放和振铃计数变化规律较为相似．可以清楚地发现,在试验过程中大部分时间内, 能量释放、振铃计数比较均衡, 但是存在某些大幅度突变的时间点, 说明在出现大量能量释放和振铃计数之前, 梁内部是处于累积能量的过程．而高能量、多振铃计数的突变点,往往象征着材料内部裂纹发生剧烈变化．所以根据两者的变化规律,将钢筋混凝土梁四点弯曲试验从开始加载直至破坏的过程分为4个阶段: 1) 0～103 s, 加载初期几乎没有能量释放以及振铃计数出现, 原因是刚开始施加的载荷较小, 这部分载荷将制作混凝土时原有的孔隙、微裂纹压实, 可以认为梁发生弹性变形．加载到约6 kN时, 声发射能量开始出现幅度小、稍密集的变化,直至载荷达到约16 kN, 声发射能量出现第一个峰值(7 208 mV·μs), AE信号密集出现, 前面累积的能量一瞬间在此刻释放, 说明梁内部形成微破裂带, 但试件表面未见宏观裂纹; 2) 103～489 s, 通过第一个峰值能量的集中释放后, 能量释放比较缓慢, 进入稳定的阶段．随着第二级加载阶段荷载的增加, 能量与振铃计数出现小幅度波动, 说明混凝土新微裂纹不断增多或旧的裂纹继续向梁上缘扩展,同时伴有斜向的扩展趋势．第489秒加载至约54 kN时, 能量出现第二个峰值点(47 619 mV·μs), 也是试验过程中最大的点,振铃计数高达62 212, 宏观裂纹产生, 结构出现较为严重的损伤; 3) 488～1 151 s由于骨料的阻裂作用, 峰值后再次出现较为稳定的裂纹扩展的阶段．虽然载荷在增加, 但是能量、振铃计数连续3个加载阶段处于较低的水平．新裂纹仍然不断出现, 原先的裂纹继续向上扩展,宽度也在不断增长, 但由于钢筋的作用会限制一部分裂纹扩展．至第1 152秒载荷达到约112 kN时再次出现峰值点(14 877 mV·μs), 这是混凝土结构失效的前兆; 4) 1 152 s后, 加载曲线发生弯曲且载荷出现2次较为明显的下降, 混凝土即将达到极限荷载, 第1 205秒载荷达到最大值117.7 kN, 第1 210 秒出现试验过程中第二大能量峰值点(27 755 mV·μs), 振铃计数为48 348, 混凝土失去承载能力, 梁失稳断裂, 总体裂纹如图4所示, 图中裂纹已作黑色加深处理．

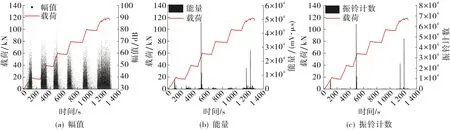
图3 钢筋混凝土梁声发射参数历程图Fig.3 The process of AE parameters of reinforced concrete beam

图4 钢筋混凝土梁总体裂纹Fig.4 Cracks in total on the reinforced concrete beam

图5为素混凝土梁四点弯曲声发射主要参数随时间变化规律的图像．整体加载过程较为缓慢, 微裂纹缓慢形成, 载荷能够较好地保持线性关系．图5(a)显示, 素混凝土梁在连续加载过程中, 声发射事件幅值主要集中于40 dB以下, 第30秒载荷达到3.1 kN时, 出现第一个幅值较高的事件(49.1 dB)．之后, 随着载荷的不断增加, 幅值大于4 dB事件间断出现,高幅值声发射事件大多集中出现在结构断裂失稳的时间前后, 第104秒梁断裂时刻连续出现多个高于9 dB的事件．根据图5(b), 可以将素混凝土梁加载过程分为4个阶段: 1) 0～30 s, 刚开始施加的载荷水平较低, 声发射源来自素混凝土内部孔隙, 信号呈现出低幅值、低能量释放的特点．第30秒应力水平约为2%,能量出现第一个峰值(25 mV·μs), 梁跨中下缘出现第一条裂纹; 2) 30～75 s, 该阶段裂纹处于稳定增长, 幅值及能量大小有一定的增加．期间出现几次与第一个峰值大小接近的能量释放, 说明混凝土梁原先裂纹扩展的同时不断有新的微裂纹产生, 损伤缓慢积累．第75秒能量释放达52 mV·μs, 但是试件内部的大量骨料阻碍了裂纹的进一步扩展, 梁的承载力依然较大; 3) 75～104 s, 整体裂纹活动比前一阶段更活跃, 微裂纹贯通,形成微破裂带．第89秒载荷达到12.5 kN, 应力水平约为80%, 再次出现能量释放的高峰(174 mV·μs), 宏观裂纹出现; 裂纹尖端受到粗骨料阻裂作用, 累积的能量在该阶段释放, 能量大小呈指数迅速增长, 表现为裂纹长度和宽度快速增大．在第104秒出现试验过程中最大的能量释放(50 246 mV·μs), 伴随着崩裂声, 梁体从中部断开最终裂纹情况如图6所示; 4) 104 s后, 试件破坏且载荷急剧减小, 声发射事件仍较为活跃, 能量释放逐渐减小, 直至消失．约90%的声发射事件振铃计数小于50, 说明整个试验过程中微裂纹扩展占主要地位, 仅在第104秒混凝土梁断裂前后出现多个振铃计数超过700的声发射事件, 最大振铃计数达10 173(见图5(c))．

图5 素混凝土梁声发射参数历程图Fig.5 The process of AE parameters of plain concrete beam

图6 素混凝土梁破坏后的裂纹Fig.6 The crack of plain concrete beam after its failure

3.2 b值与ba值对比分析

根据钢筋混凝土梁加载情况, 将每级加载过程分为3个部分: Kaiser效应阶段(第一级加载阶段没有此阶段)、有效加载阶段和载荷保持阶段．由于在载荷保持阶段仍存在小幅度卸载情况, 所以在下一级加载阶段初期会出现Kaiser效应(加载到原先最大载荷前不会产生明显的声发射现象)．将每个有效加载阶段及载荷保持阶段根据时间平均分为3段分别计算b值, 最后破坏阶段以每30 s的声发射事件数计算, 得到相应的b值和ba值随时间变化规律的曲线, 如图7和8所示．第一级有效加载阶段,b值即从2.530降至1.269, 载荷保持阶段又升至3.287, 为试验过程中最大值．b值增大, 甚至出现峰值, 表明声发射事件中小幅值的事件占比加大, 微裂纹增加;b值减小象征大幅值的事件增多, 大尺度的裂纹数量增多, 甚至可以在试件表面看到宏观裂纹[20-21]．之后各阶段(除Kaiser效应阶段外)b值在0.99～1.7之间波动．由于第一级加载阶段载荷较小, 声发射信号主要来自原始缺陷和闭合裂纹相互摩擦作用, 导致第二级Kaiser效应阶段可逆位错恢复原状时仍有较多的声发射事件产生, Kaiser效应不明显．从第三级加载阶段开始, 缺陷以不可逆的微裂纹为主, 钢筋混凝土梁出现较为明显的Kaiser效应．此后的各级Kaiser效应阶段声发射事件数量较少, 导致拟合所得的a、b值均很小, 出现多个b值在0.5左右的数值“不可靠点”．而每个有效加载阶段内,b值一定程度上出现小幅下降,但整体变化规律并不明显．相较于图7, 图8中ba值的变化规律与载荷曲线有着良好的对应关系．通过固定a值的方法,将原本“不可靠点”变为“可靠点”．从图8中可以明显地看出,在有效加载阶段ba值连续下降, 且每级有效加载阶段前1/3时间下降幅度最大; 而在载荷保持期及Kaiser效应期,ba值上升．

图7 钢筋混凝土梁b值与载荷随时间变化曲线Fig.7 Curve of b-value and load of reinforced concrete beam with time

图8 钢筋混凝土梁ba值与载荷随时间变化曲线Fig.8 Curve of ba-value and load of reinforced concrete beam with time

为了进一步说明ba值在整个加载过程中的变化规律, 将其与声发射基本参数作对比, 结果如图9所示．从图9(a)可以发现, 声发射事件大部分都出现在ba值下降的阶段,且均出现在ba值曲线极小值点附近．结构失稳断裂前后大量的事件集中出现,ba值保持在1.129～1.294．钢筋屈服前, 第489秒第一条裂纹局部水平开裂形成宏观裂纹, 同时右侧即将形成第二条宏观裂纹; 第1 152秒第一条裂纹已形成较大的贯穿性裂纹, 右侧裂纹迅速向上扩展．图9(b)和(c)中, 点A(第490秒)和点B(第1 143秒)均处于ba值连续下降段, 且接近局部极小值, 这2个时间点附近均出现较大的能量释放与振铃计数, 表明ba值可以反映声发射能量、振铃计数的变化, 从而预示结构出现损伤的严重程度．

图9 钢筋混凝土梁ba值与声发射基本参数的比较Fig.9 Comparison of ba-value and AE parameters of reinforced concrete beam

素混凝土梁四点弯曲在匀速加载的过程中以每5 s的声发射事件作为一组数据, 相应的b值与ba值如图10～11所示．加载前期声发射事件数量较少, 且信号幅值集中在29.5～34.5 dB, 认为是b值数据“不可靠点”; 50～75 s,b值在2.0～3.5之间波动; 75～80 s, 载荷由9.55 kN升至10.5 kN(应力水平达到65.7%),b值出现迅速下降, 并维持在1.5左右的较低水平; 第105秒混凝土已达到极限承载力, 发生断裂破坏, 此时b值最小值; 梁断裂后b值又呈现上升的状态．由于结构实际断裂失效的时间为104 s, 100～105 s时间窗内计算的b值包含了结构断裂时的声发射信号, 故不能起到预测梁失效的作用．图11结果显示,ba值的变化更有规律, 其变化过程分为4个阶段: 平稳阶段、小幅波动阶段、连续下降阶段、重新上升阶段．由于ba值是基于b值计算的优化值, 100～105 s内计算的ba值同样包含了断裂时的信号数据, 故不能简单地将ba值达到最小值作为结构断裂的前兆, 而应以其连续下降的趋势作为结构损伤的预警信号．

图10 素混凝土梁b值与荷载随时间变化曲线Fig.10 Curve of b-value and load of plain concrete beam with time

图11 素混凝土梁ba值与载荷随时间变化曲线Fig.11 Curve of ba-value and load of plain concrete beam with time

图12为ba值与声发射基本参数结果比较图．结果显示, 加载前期ba值前期维持在3左右的较高水平, 对应能量几乎为零, 幅值集中于29.5～34.5 dB的声发射平静期; 50～75 s,ba值小幅度波动, 出现稍高幅值和几处能量的突变, 此阶段素混凝土梁以微裂纹萌发、扩展为主; 从第75秒开始至最终破坏, 跨中2处微裂纹汇聚形成一条宏观裂纹的扩展、贯穿, 其中点C(第75秒)至点D(第100秒)之间连续多个时间窗ba值出现下降(从3.001降至1.843), 能量释放频率及大小都有显著提升,裂纹逐渐由小尺度转为大尺度, 最终失稳破坏时刻大幅值、高能量、多振铃计数声发射事件出现．梁破坏后, 声发射事件幅值逐渐减小,ba值再次呈现出上升的趋势．通过素混凝土梁四点弯曲试验同样说明ba值的变化规律能够反映声发射事件基本参数的变化, 并以此判断结构的损伤程度．