基于刀位文件的空间复杂曲面机器人加工技术研究*
2021-11-09杨启正涂宇雷先华胡自化秦长江
杨启正, 涂宇, 雷先华, 胡自化, 秦长江
(1.湖南交通工程学院,湖南 衡阳 421007;2.湘潭大学 机械工程学院,湖南 湘潭 411105)
0 引言
随着工业机器人技术的发展,在大规模重复性劳作中,工业机器人逐渐发挥了越来越大的作用,但作为一种强大而又灵活的加工设备,工业机器人不应该仅仅局限于简单的搬运、码垛等劳作.由于工业机器人的多自由度,在空间复杂曲面加工中比数控机床有较大的优势,所以对于空间复杂曲面,利用机器人加工是必然趋势.但目前的研究大都集中在利用G代码的机器人空间路径规划,该方法对于平面加工有一定的优势,但是对于复杂空间曲面的加工较为困难,且机器人空间姿态难以较好地控制,很多情况下需要人工干涉来调整姿态[1].这就对利用机器人进行空间曲面的加工有了更高的要求.
根据UG可变轮廓铣中生成的刀位文件的特点,利用该刀位文件实现机器人末端位姿的计算.由于加工的是较小的空间曲面零件,在机器人工作空间内将该零件摆到合适的位置,实现工件坐标系和机器人坐标系的标定,进而利用逆运动学来计算机器人各个关节角的值,在不考虑避障的情况下,根据“最短行程”来选择合适的逆解,将各个加工点所对应的机器人关节角求解出来,以求解出的各个关节角值来驱动机器人运动,实现复杂空间曲面的柔性精准加工.
1 机器人正逆运动学求解
本文以瑞士ABB公司生产的IRB140六自由度工业机器人为仿真加工机器人,该工业机器人是串联型,依据转动关节的D-H法建立坐标系,如图1所示[2],该坐标系用四个参数来描述两关节轴线沿共垂线的距离ai,称为连杆长度,垂直于ai在平面内两轴线的夹角αi,称为连杆扭角;沿关节轴线i的两个公垂线的距离di,称为连杆距离,垂直于关节i轴线的平面内两公垂线的夹角θi,称为连杆夹角.确定各连杆D-H参数,即可以得到如表1所示的连杆参数表.然后根据相邻两杆之间的变换公式就可以求得机器人末端执行器关于机器人基坐标的变换关系[3].
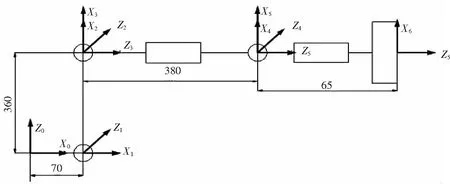
图1 IRB140机器人D-H坐标系Fig.1 D-H coordinate system of IRB140 robot
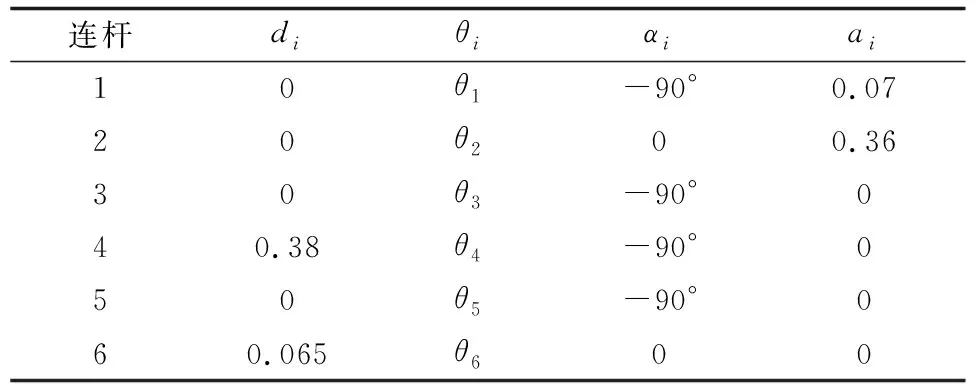
表1 IRB140机器人连杆参数表
相邻的两连杆变换齐次坐标矩阵表示为:
.
(1)
其中:cθi=cos(θi);sθi=sin(θi);i=1,2,…,6.
该齐次坐标变换矩阵能够描述连杆坐标系之间相对平移和旋转的齐次变换,Ai分别描述第i个连杆相对基座的位置和姿态,在六自由度工业机器人中,如果知道末端执行器在最后一个坐标系下的坐标,那么通过齐次变换矩阵相乘可以得到该坐标相对在基坐标系的位置和姿态,相乘关系式如下所示:
0T6=A1A2A3A4A5A6
.
(2)
1.1 逆运动学求解
采用分离变量法来求解机器人逆解,常规求法是用一系列变换的逆矩阵Ai-1左乘,然后找出左乘后右端的常数项,同时让左端相对应的项与之相等,进而利用三角函数来求得相应的关节角,此方法要求六次才能求得全部的解.利用A1-1A2-1TA6-1=A3A4A5可一次性求得机器人各个关节角,这样就省去了连续左乘逆矩阵的烦琐性.对于一般的六自由度机器人不存在封闭解,但是当该机器人后三个相邻关节轴线交于一点或是平行时[4],就符合解耦机器人特点,具有封闭解,本文分析的IRB140工业机器人的最后三个关节轴线相交于一点,符合解耦机器人的特点,所以该机器人最多有八组逆解.三角函数求解关节角时由于arctan(x,y)的解范围是[-90°,90°],解的范围不够精确,无法求得关节范围内全部解,而双变量反正切函数arctan 2(x,y)的取值范围是[-180°,180°],可以获得所有可能的解,解所在象限由x,y的正负来判断.各个关节角求解结果如下:
θ1=arctan 2((px-d6ax),(py-d6ay))+π/2,θ1,=arctan 2((px-d6ax),(py-d6ay))-π/2
,
(3)
θ2=arctan 2((k4/r),±sqrt (1-(k4/r)2))-arctan 2(k31,k32).
(4)
其中,
(5)
其中,
θ5=arctan 2(±sqrt (1-(k6)2),-k6),
(6)
其中,
k6=sin (θ2+θ3)k1+cos (θ2+θ3)az,
θ4=arctan 2(k7,k8),
(7)
其中,
k7=(cos (θ1)ay-sin (θ1)ax)/sin (θ5)p,
k8=(sin (θ2)az-cos (θ2)k1-sin (θ3)cos (θ5))/(cos (θ3)sin (θ5)),
θ6=arctan 2((k10+k11k12),(k12k10-k11))+π,
(8)
其中,
从以上各个关节角求解结果可知,关节角1、2、5各有两个值,所以该机器人共有八组解,但是求解出来的解不一定都符合要求,如果求出的关节角超出关节角运动范围,则要对该关节角转换上下限,也就是在求解得到的关节角的基础上加减360°,使关节角在合理的范围内[5].在无避障的要求下以各个关节角的绝对值之和最小值为逆解优化目标,选取之和最小的那一组为最优解,选取关节角时,在同一条加工轨迹上,机器人各个关节角不能有大的突变现象,在保证关节角的平稳变化的同时也保证了机器人的平稳运动.
2 机器人工作空间范围求解
基于蒙特卡洛法求解机器人工作空间.蒙特卡洛法是借助于随机抽样的方式来解决问题,通过正运动学求解,将表示末端空间位置的关系式求解出来,然后利用Matlab的rand函数产生一个随机数,在关节运动范围内产生一个关节角的随机值,最后利用Matlab软件编程求解在运动范围内的机器人末端运动空间范围,也就是机器人的工作空间范围[6].
根据正运动学求解结果,利用Matlab编程,输入随机数n的值,可求解出其工作范围,Matlab编程和求解结果如图2所示.
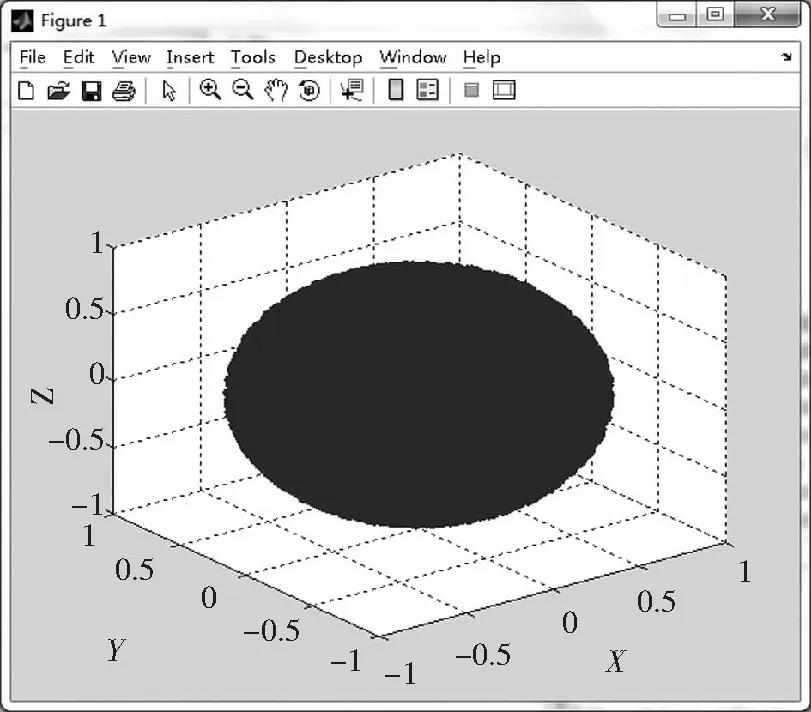
图2 机器人工作空间三维图Fig.2 Three dimensional diagram of robot workspace
从分析结果可知机器人工作空间范围是X∈[-0.873 6,0.873 9],Y∈[-0.872 6,0.872 9],Z∈[-0.805 0,0.805 0].该结果对下一步工件移动范围有参考作用.
机器人工作空间求解精度取决于n值的大小,当n分别取500、4 000、10 000时工作空间精度如图3所示.
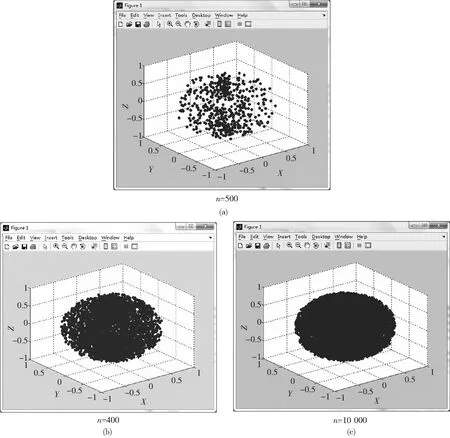
图3 n=500、4 000、10 000时工作空间精度Fig.3 The spatial working accuracy of n=500、4 000、10 000
3 加工轨迹的生成
UG加工数控模块为所有加工提供一个相同、界面友好的图形化窗口环境,用户可以在图形方式下观测刀具沿轨迹运动的情况,并可对其进行图形化修改,如刀具轨迹进行延伸、缩短或修改.该模块同时也提供通用的点位加工编程功能,可用于钻孔、攻丝和镗孔等加工编程,该模块交互界面可按用户需求进行灵活的用户化修改和剪裁,并可定义标准化刀具、加工工艺参数样板库,使初加工、半精加工、精加工等操作的常用参数标准化[7].
利用UG系统为曲面轮廓铣提供的对刀轴控制、走刀方式选择和刀具路径生成功能,可以在UG中加工任何几何体.在UG/CAM模块中对叶轮曲面进行可变轮廓铣仿真加工,设计合适的加工刀具,选择合理的加工参数,分别对叶轮的流道面和叶片面进行粗精加工.刀具轨迹规划如图4所示,并获得刀具轨迹数据[8],最后以txt文件格式导出叶轮加工的刀位文件.本文以一个流道面的清根加工为例,实现本文所述方法的仿真加工,流道面加工轨迹虚拟模型如图5所示.
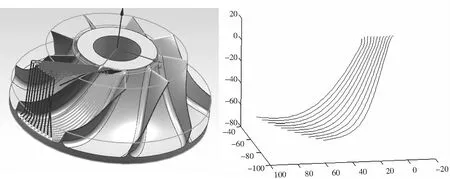
图4 叶轮流道面的加工 图5 流道面加工轨迹虚拟模型Fig 4 Machining of impeller runner surface Fig 5 Virtual model of machining path of runner surface
3.1 加工信息处理
刀位文件格式是GOTO/X,Y,Z,I,J,K,其中X,Y,Z代表的是刀尖在加工坐标系下的空间位置,I,J,K代表刀轴矢量.对于空间姿态来说,上述六个信息为有用信息,其他加工参数信息暂时不做考虑,将有用的加工信息提取出来,以txt格式保存.对刀位文件处理过程中我们求得的是在工件坐标系下的位姿.由于对整个叶轮的加工点提取工作量较为巨大,因此选取流道面加工的一条空间加工轨迹来实现运动仿真.提取的信息以文件名2date保存在Matlab文件夹中,以便后续仿真时信息的调用.
3.2 末端位姿获取方法
刀位点的刀轴矢量N可以直接通过刀位文件的I,J,K直接得到,刀位点的切向矢量T则通过下一个加工点的坐标获得.因为表示空间姿态的三个矢量是单位矢量且相互垂直,加工过程由第一点向第二点方向,以此加工下去.空间姿态坐标系如图6所示,假设第一点的坐标为P1(X1,Y1,Z1),第二点的坐标为P2(X2,Y2,Z2),将I,J,K平移到以P1为起点的位置,相对应的坐标值分别增加P1的坐标值,通过点P1作与向量P1N相互垂直的平面S,由P2作平行于Z轴的直线L,直线L与平面S的交点为P3,P3的X,Y轴方向的坐标值与P2相同,Z轴方向坐标值是未知的.向量P1N与向量P1P3相互垂直,相乘为0,故可以求出Z3值,然后将向量P1P3简化为单位向量,切向矢量由此求得.副法向矢量B则通过刀轴矢量N和切向矢量T叉乘得到[9],由此就得到了在工件坐标系下的刀位点的空间姿态.
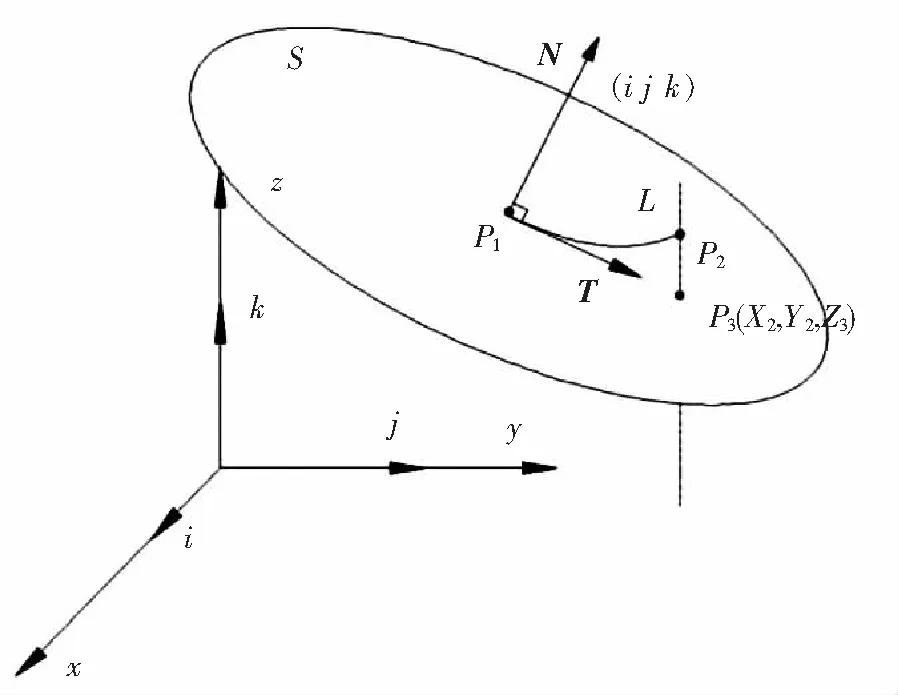
图6 空间位姿坐标系Fig 6 Spatial pose coordinate system
4 仿真对比
对于小型空间曲面零件加工来说,可以采用多轴机床加工的标定方法,在机器人坐标系中将工件摆到模型所在位置,实现机器人坐标系和工件坐标系的标定.如果是大型工件,则需要工件坐标系的标定.因为本文是针对小型空间曲面的加工,在上文求得的机器人工作空间范围内移动工件,使其处在合适的加工位置,避免求得关节角超程或是奇异点的出现,即将刀位文件的X,Y,Z在机器人空间范围内加减相应的值来获得合理的位姿. 利用Matlab进行编程,实现刀位文件到机器人各关节角度的转换,选取最优解,以最优解来驱动机器人运动,实现虚拟机器人的运动,最后将机器人轨迹与实际UG加工轨迹进行对比,其具体仿真流程图如图7所示.
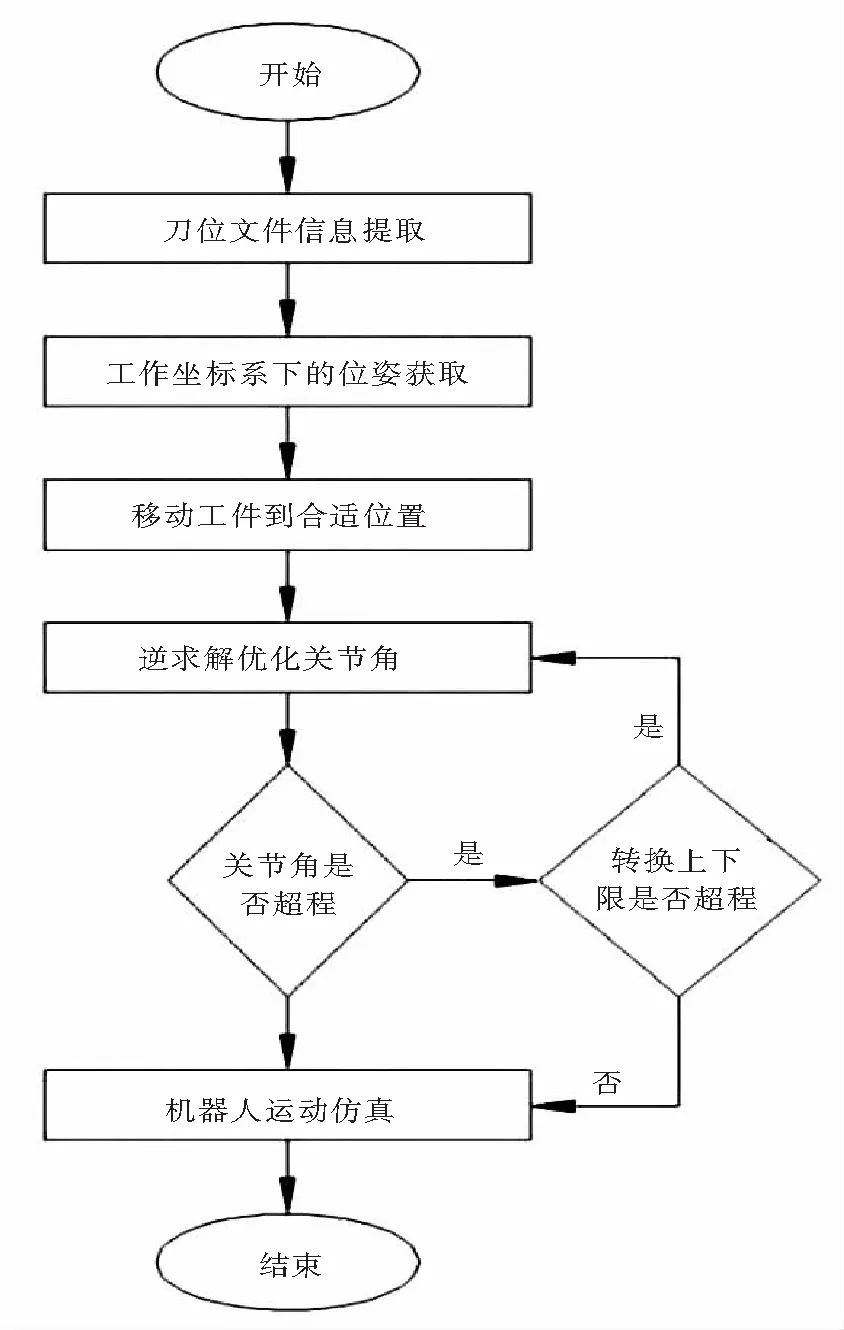
图7 刀位文件转换流程图Fig 7 Flow chart of tool position file conversion
用Matlab进行编程,将刀位文件转换为机器人加工的位姿,处理结果如图8和图9所示,用link函数建立机器人虚拟模型,编写相应的程序,用得到的关节角驱动机器人仿真运动机,机器人运动瞬间如图10所示,末端轨迹曲线如图11所示,最后将机器人末端轨迹与UG加工轨迹进行对比如表2所示.
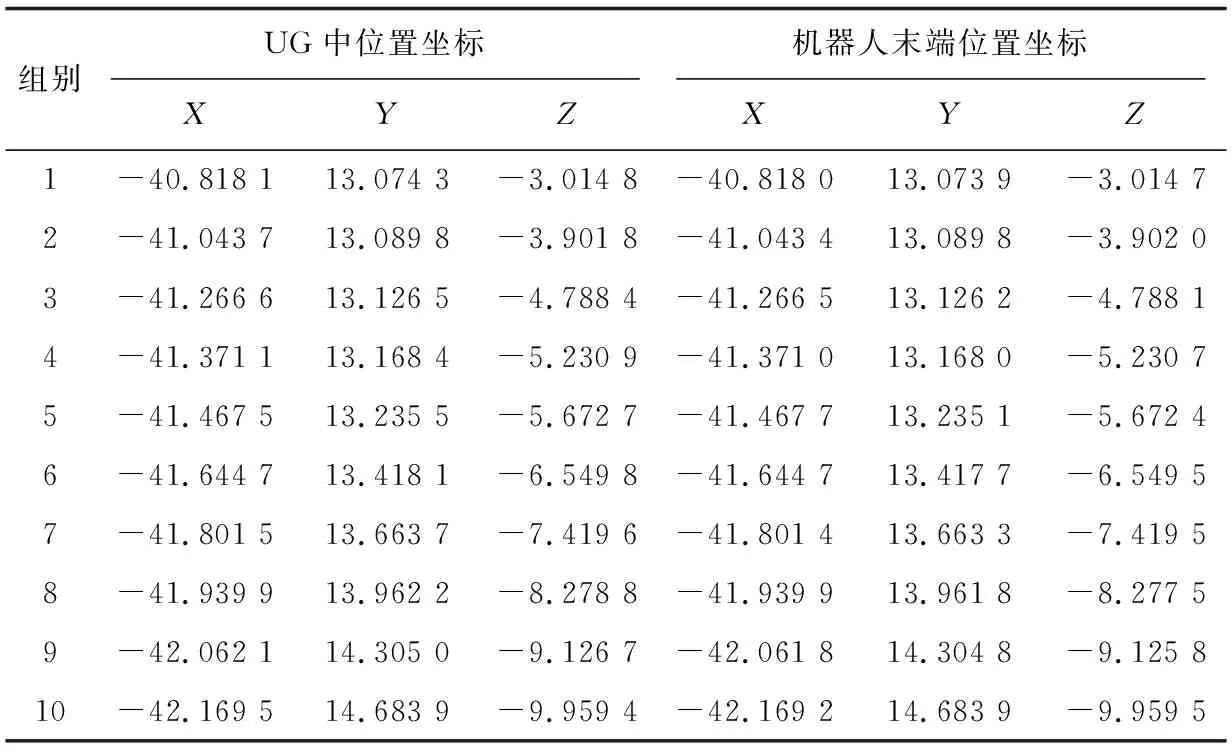
表2 UG位置坐标与机器人末端位置坐标比较
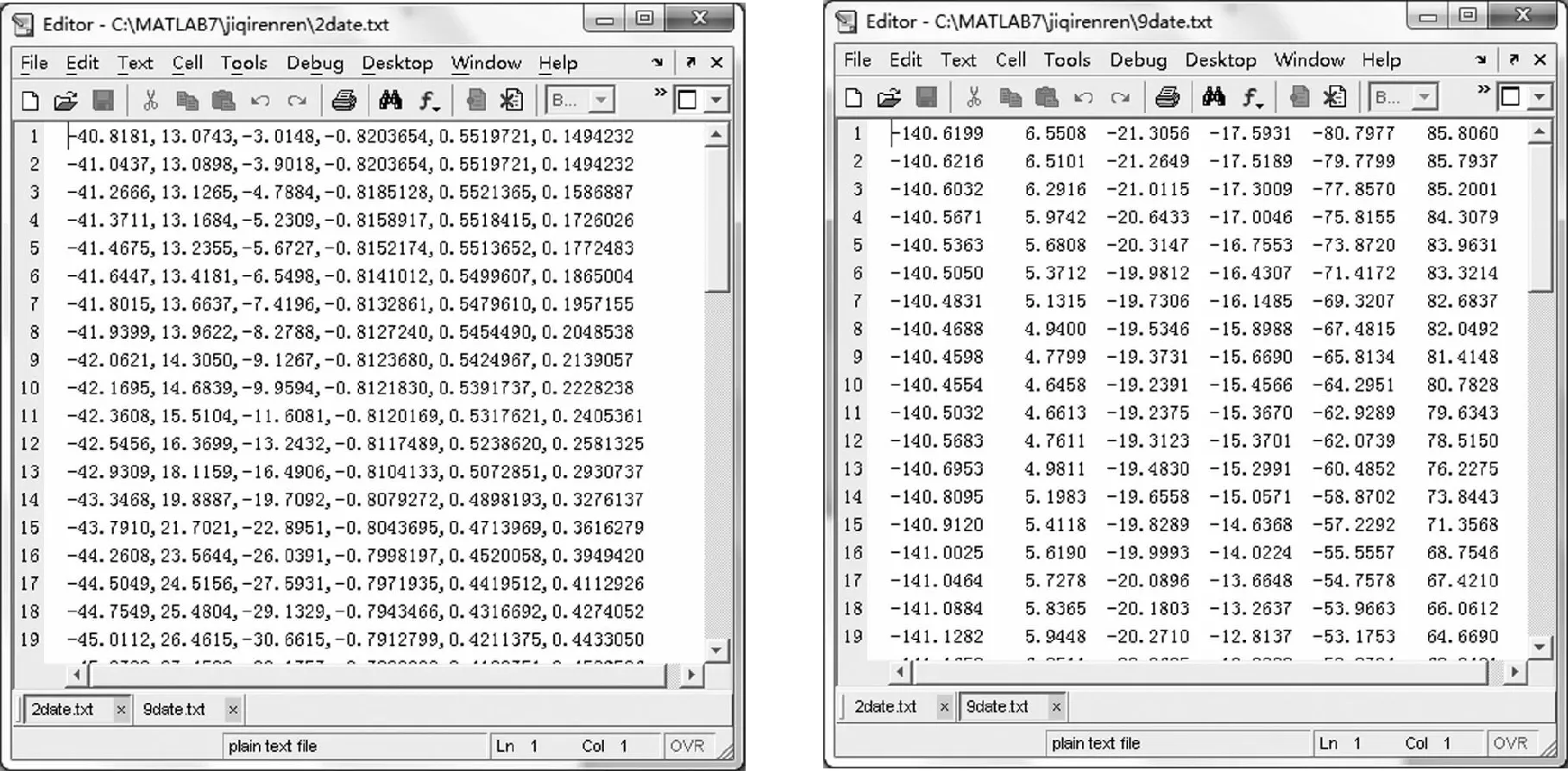
图8 刀位文件提取信息 图9 对应各个关节角值Fig 8 Extraction information of tool position file Fig 9 Corresponding joint angle values
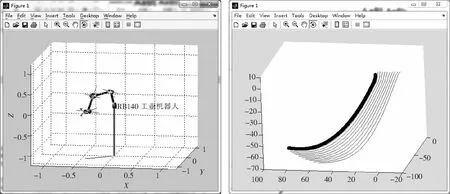
图10 机器人模拟运动瞬间 图11 机器人末端轨迹曲线Fig 10 Robot simulation movement moment Fig 11 Robot end trajectory curve
5 结论
运用机器人自由度高的特点,结合现有的CAM软件的优势,实现空间复杂曲面的高效加工,避免人工示教的烦琐和利用G代码无法获取空间姿态的缺点.最后经过仿真模拟,验证了利用此方法把刀位文件转换为机器人末端位姿的正确性和可行性,为实现机器人高效率高精度加工空间复杂曲面奠定一定的基础.
在UG轨迹线上和机器人末端轨迹线上分别对应选取10个点,从表2对比可以发现,X轴方向的最大误差为0.000 3 mm,Y方向最大误差为0.000 6 mm,Z方向最大误差为0.000 9 mm,这在加工中是完全可以忽略不计的.所以两条加工轨迹基本相同,重合度较高,验证了利用此方法可以实现从刀位文件到机器人末端执行器运动的转换.
