基于响应面的空心活塞杆轻量化设计*

李卫民 潘士超

(辽宁工业大学机械工程与自动化学院，辽宁 锦州 121001)

未来汽车发展的主要方向是新能源汽车，续航能力则是其发展的关键问题。轻量化设计是实现新能源汽车综合性能提升的重要途径之一，是轻量化汽车产品开发的前提和基础。

汽车的轻量化可以提高汽车的转向响应、操控稳定性及安全性，在节省材料的同时也能有效降低制造成本。当汽车车身重量减轻时，汽车将具有更高的加速度；同时汽车自身惯性也会减小，进而缩短刹车距离。新能源汽车的轻量化能够切实提升电动汽车的续航能力。为了从根本上提升电动汽车运行过程中的质量与效率，应当给予电动汽车结构轻量化的相关研究以足够的重视。

1 活塞杆静、动态特性分析

1.1 活塞杆数学模型的建立

减振器活塞杆材料选用45#钢，密度为7 890 kg/m3，杨氏模量2.09×105MPa，泊松比为0.269，屈服强度为355 MPa。利用ANSYS Workbench与SolidWorks的协同接口，在SolidWorks中进行变量化建模，其数学模型如图1所示。

1.2 外加载荷及边界条件的确定

在对减振器活塞杆进行静力学校核过程中，应取其最大受力工况进行分析。根据减振器的工作原理和结构特点，分析减振器的阻尼特性，确定了活塞杆轴向受力为1 470 N。对减振器活塞杆的非活塞端施加固定约束，另一端施加轴向载荷。

1.3 活塞杆静态特性分析

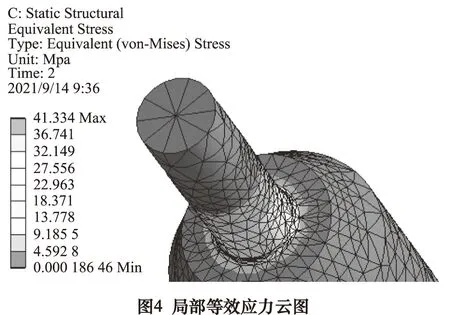
静力学求解后减振器活塞杆的位移云图以及等效应力云图，如图2～4所示。

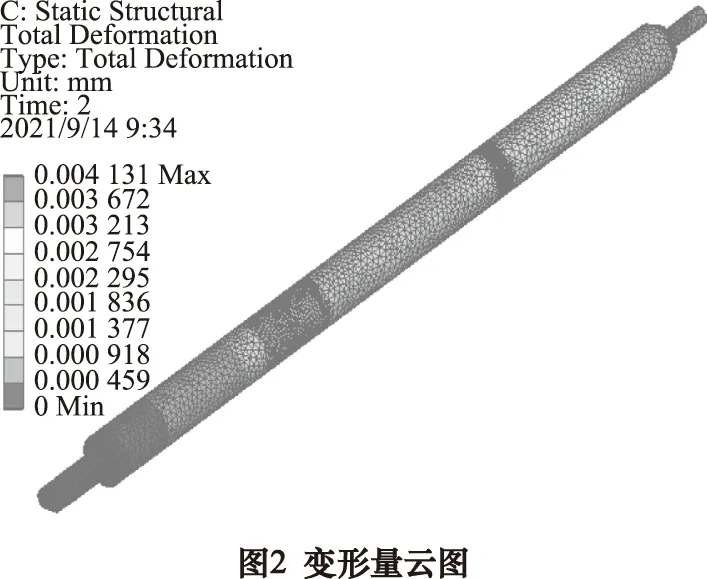
由图2、图3、图4可知，活塞杆最大位移量约为0.016 mm，最大等效应力数值为41.33 MPa，其数值远小于45#钢的屈服强度，应力较大值主要出现直径突变位置，此处为应力集中。综合评价，减振器活塞杆的结构强度有较大冗余，可进行活塞杆的轻量化优化设计。

1.4 减振器活塞杆动态特性分析

车辆行驶过程中，当外部的激振频率接近于减振器的固有频率时，会引起整机的共振，对车辆行驶的稳定性和安全性有所影响。通过模态数值仿真分析活塞杆的固有频率并加以调整，避让易产生共振的频率区间。减振器活塞杆的低阶模态对整体结构的影响比较显著，通过ANSYS Workbench中的Modal模块，进行模态的数值仿真，得到了减振器活塞杆的前4阶自由振动模态，模态分布及振型如表1所示。

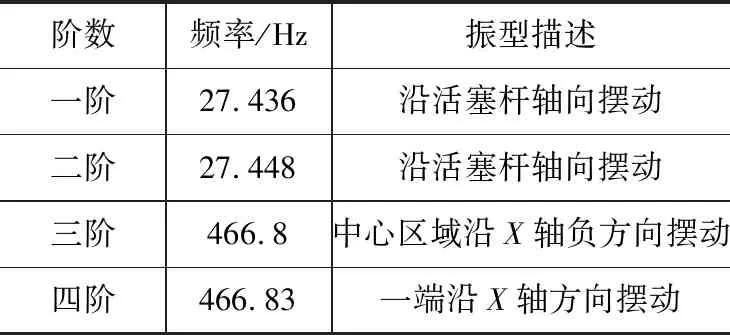
表1 活塞杆低阶固有频率

研究表明，在常规路况下的激振频率如表2所示，为避开共振频率区间，常将低阶模态频率控制在30～100 Hz[1]。表2 常见汽车激振频率

外界激励路面车辆内部电机激振空气流动频率范围/Hz1～35～15>175>200

2 减振器空心活塞杆的多目标优化

2.1 减振器空心活塞杆优化设计变量的确定

减振器空心活塞杆是空心轴类，空心区域的直径和长度对减振器空心活塞杆静动态特性有重要影响。为了提高减振器空心活塞杆的综合性能并减轻整体质量，选取了减振器空心活塞杆的6个主要参数作为减振器空心活塞杆优化设计中的设计变量，如图5所示。各变量变化范围，如表3所示。

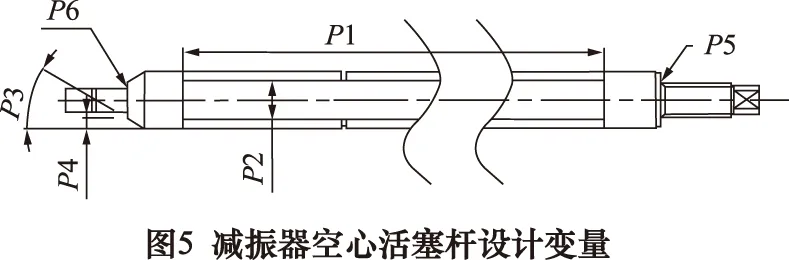
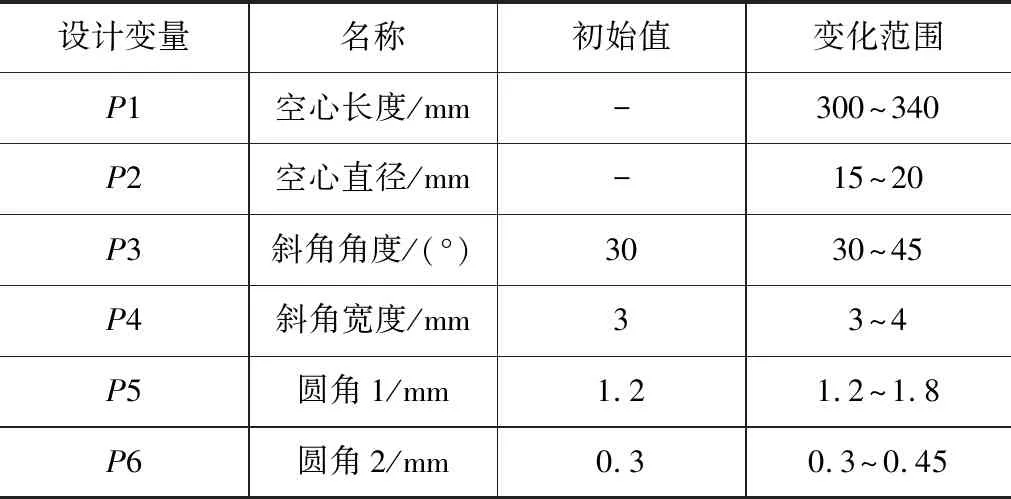
表3 减振器空心活塞杆设计变量变化范围

2.2 DOE试验设计

DOE试验设计可确定更为合理的试验设计点。中心复合试验设计(CCD)能以最少的试验循环提供关于试验变量和试验误差的诸多信息[2]。

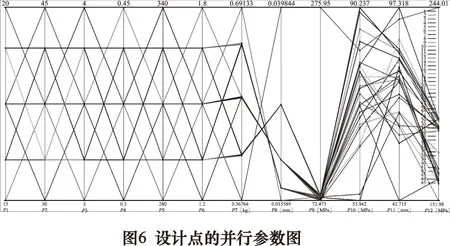
在ANSYS Workbench中对振器空心活塞杆进行试验设计，试验类型选择中心复合试验设计，设计变量共6个，共生成了45个试验设计点。以减振器空心活塞杆的质量、低阶模态频率、等效应力和变形量作为目标变量。在ANSYS Workbench的Design of Experiments模块下进行数据更新，求解每一个试验设计点。所得到的部分实验设计点及求解结果如表4所示。每个设计点产生的并行参数图，如图6所示。

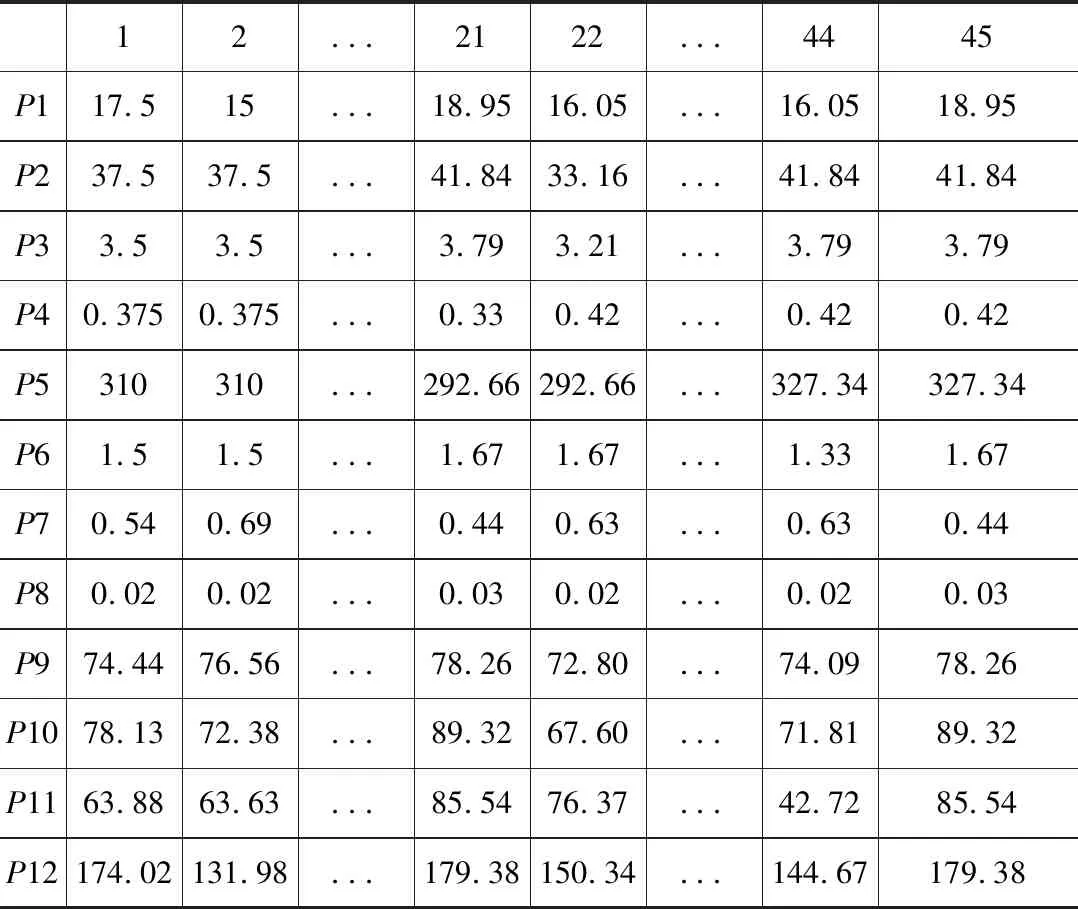
表4 部分样本点数据

3 基于响应面法的多目标优化设计

响应面优化设计方法是通过筛选试验设计点的方式来寻找隐式函数的显性多项式方程[3]。为了评价空心活塞杆优化后的效果，设置优化后空心活塞杆质量最小和低阶模态频率最高为目标函数，同时考虑减振器活塞杆的强度与刚度要求。减振器空心活塞杆优化设计的数学模型为：

varx=[x1,x2,x3,x4,x5,x6]

obj minf(x)=m

maxf(x)=f

minf(x)=δ

minf(x)=σ

3.1 响应面模型的构建

在响应曲面模型中，将x和y分别作为设计变量和目标输出，两者间的函数关系可以表示为：

Y=y(x)+ε

(1)

式中：y(x)是未知函数，ε是函数的误差。x是多维独立的设计变量即:

x=[x1,x2,...,xn]

(2)

其中设计目标和目标输入之间的关系可以用多项式来表示为：

(3)

3.2 响应面拟合与精度验证

在ANSYS Workbench中对响应面的拟合精度根据决定系数(R2)进行评价，R2反映了构建的响应面函数符合给定数据的近似程度，数值范围为[0,1][4]。较好地逼近要求R2≥0.9，若R2=1，则可认为构建的近似函数可以准确地描述系统响应值的变化。

当采用遗传聚类法拟合时，输出参数的决定系数，如图7所示。当采用标准响应面全二次多项式法拟合时，输出参数的决定系数，如图8所示。当采用克里金法拟合时，输出参数的决定系数，如图9所示。

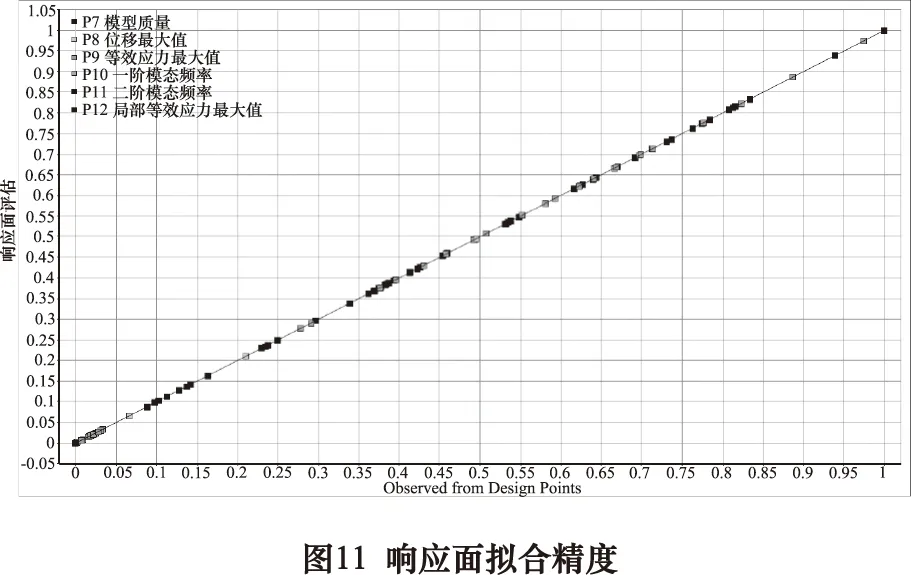
观察图中决定系数值可知，当采用遗传聚类法进行响应面拟合时，每个输出变量的决定系数可以达到0.99以上；但采用Kriging插值法进行拟合时，输出参数的决定系数值均为1，均达到了最佳拟合效果，能够高效且精准地完成响应面模型的建立。因此本文选用 Kriging插值法完成减振器空心活塞杆响应面模型的建立，所建立的3D响应面如图10所示，所构成响应面的拟合精度如图11所示。

3.3 灵敏度分析

在对结构进行优化设计时，通常对结构性能的影响往往是多个设计变量共同作用的结果。经由灵敏度直方图可较为容易地找出多个设计变量中对结构性能影响较大一个变量或几个变量，从而将他们作为优化设计中的关键变量进行设计。

一阶灵敏度可表示为：

(4)

式中：Δp是设计设计参数的改变量。

灵敏度数值的大小表明了参数值的变化对函数整体变化的影响程度。在对减振器空心活塞杆进行优化设计时，通过比较各设计变量的灵敏度参数值，选取对减振器空心活塞杆的动静态特性有显著影响的设计变量。

减振器空心活塞杆设计变量与输出参数之间的灵敏度关系如图12所示。可知，在对减振器空心活塞杆质量的影响上，设计变量P1的影响最大，且为负相关，其他各设计变量对质量的影响较小。设计变量P1对减振器整体等效应力与最大变形量的影响最大，并且为正相关关系。在对减振器空心活塞杆低阶固有频率的影响上，各设计变量对低阶模态均有明显的影响。在对减振器空心活塞杆承受横向载荷问题上，设计变量P1、P2、P3、P5对最大等效应力呈正相关关系，设计变量P4、P6对其呈负相关关系，且设计变量P1对其影响最大。

3.4 多目标优化

在多目标优化问题中，由于难以同时实现多个目标之间的最优解，往往会产生一系列的有效解，也叫做Pareto解[5]。在计算得到均衡分布的Pareto最优解之后，根据零部件设计要求和工程实际经验，选择最合理的优化结果。减振器空心活塞杆响应面优化设计分析流程如图13所示。

在响应面模型基础上，选用多目标遗传优化算法(MOGA)进行优化求解。MOGA算法是利用遗传算法的通用方法来有效地解决多个需要同时优化的问题，并求得多个目标函数之间的最优解[6]。以减振器空心活塞杆质量最小、变形量最小和低阶固有频率最大为设计目标，采用多目标遗传算法进行迭代优化求解。经16 455次迭代后收敛，得到了5个候选点(Pareto最优解)，如表5所示。

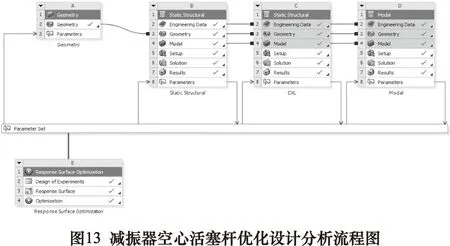
表5 候选点结果

将优选候选点结果经过星级对比后，选择候选点5作为新的设计点并对设计变量值进行取整处理，优化前后的尺寸变化对比如表6所示。优化后的减振器空心活塞杆总变形量及等效应力值均有小幅度增加，但都在材料的许用范围以内，并且空心活塞杆可承受一定的横向载荷，可满足减振器的基本工况的使用要求。主要优化目标空心活塞杆的质量由1.106 kg减重到0.45 kg，减重约60%，轻量化效果明显且其力学性能满足减振器的使用工况要求。

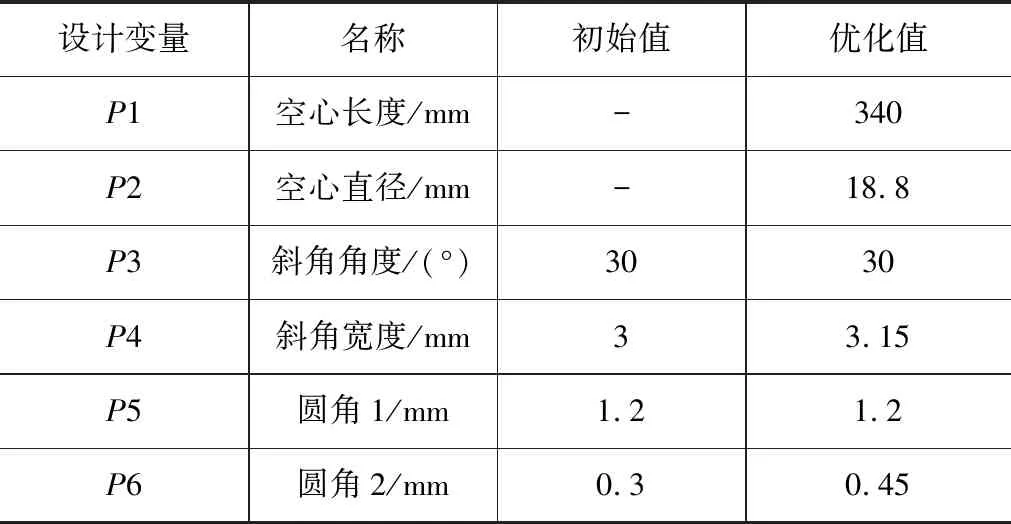
表6 优化前后设计变量变化对比

4 结语

本文以减振器活塞杆为研究对象，进行了静动态特性分析并完成了优化设计。通过对减振器活塞杆的静力学校核验证了减振器活塞杆的设计能够满足使用需求，但材料存在一定冗余现象。随后在多目标优化设计中通过中心复合实验设计对空心直径、空心区域等6个设计变量进行了试验设计，共得到45个试验点，通过灵敏度计算，得到更有效的优化设计变量。对减振器空心活塞杆进行响应面优化，使得减振器空心活塞杆质量减少到0.45 kg，减重约60%，并提升了低阶固有频率，避免了产生共振的可能性，实现了在特定约束条件下进行轻量化的目标。针对减振器空心活塞杆轻量化设计的多目标优化方法进行了探索，并比较了各种响应面的拟合精度，可为其他复杂零部件的轻量化优化设计提供一定的参考依据。