借助TI图形计算器培养数学核心素养

杜东仪

(广东省广州市从化区第二中学 广东广州 510900)

《普通高中数学课程标准（2017年版）》在课程“基本理念”中提出了“高中数学课程以学生发展为本，落实立德树人的根本任务，培育科学精神和创新意识，提升数学学科核心素养”的课程理念。同时指出：“高中阶段数学核心素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析。”数学核心素养是数学课程目标的集中体现，是学生在数学学习过程中逐步形成的，通过对高中数学的学习，学生的数学素养可得到进一步提升，从而促进学生综合能力的提高。

一、在概念教学中提高学生的抽象素养

数学概念能够揭示事物的数量关系、结构关系、空间形式等本质属性，有着极度抽象的特点，不利于学生的理解。因此，在数学概念教学中，我们要通过大量的实例或图片展示等方式将概念具体化，然后引导学生通过事物的表象分析，舍去事物的一切物理属性，逐步理解数学概念。数学抽象是数学六大核心素养之首，因此，数学概念教学就成为培养和提高学生数学抽象素养的重要环节。

案例1：函数的周期性概念教学。

（一）创设情境，直观感知周期现象

1.全班朗诵：“离离原上草，一岁一枯荣。野火烧不尽，春风吹又生。”

2.重复播放一小段音乐。

3.展示三角函数的图象。

4.活动设计：

（1）师：如果今天是星期二，那么154天以后是星期几？

（2）学生：仍然是星期二

设计意图：通过展示现实生活各方面的周期性现象，让学生在直观感知中，初步形成周期性意识。

（二）抽象数学概念

1.绘制函数y=sinx的图象，设置游标a，绘制直线x=a，x=2π+a，绘制直线x=a，x=2π+a分别与y=sinx的两交点（如图1）。

图1

2.观察两个交点的纵坐标，得出：两交点纵坐标相同的结论。

3.理论抽象

（1）得出结论：对于任意的x，都有sinx=sin(2π+x)。（2）初步概括：对于任意的x，都有f(x)=f(C+x)

（3）抽象出周期的概念：一般地，对于函数f(x)，如果存在一个非零常数T，使得定义域内每一个x值，都满足f(x+T)=f(x)，那么函数f(x)就叫做周期函数，非零常数T叫做这个函数的周期。

设计意图：根据学生的认知规律，由浅入深，由生活到数学，从特殊到一般，从具体到抽象，最后用数学语言表达出数学概念。

二、在探究教学中提升学生的直观想象素养

数学探究课在传授基础知识与基本技能的过程中有着非常重要的作用。数学探究课中，学生在教师的辅助下，体验知识的形成过程，由浅入深逐步推进，在知识体验的过程中，同时感知思维的形成过程。从直观感知到理论升华，在图象等直观事物的辅助下，使数学问题得到解决，从而实现直观想象素养的提升。

探究型教学是培养直观想象素养的一个非常好的载体，在计算机的辅助下更能使探究教学的效果达到最大化。直观想象是一种存在于人脑中的思维能力，培养直观想象素养需要大量的图象和探究过程作为支撑。而TI图形计算器能够演示模拟的实物图片、三维立体模型、平面几何模型和动态变化过程等，实现思维过程的形象化，为数学探究提供良好的物质基础，在发现、探索、猜测等过程中，使学生的直观想象素养得到提升。

案例2：变量a,w,t对函数y=a sin(wx+t)图象的影响的探究。

在传统的课堂教学中，变量a,w,t对函数y=a sin(wx+t)图象的影响并不直观，很多时候依靠的是学生的凭空想象，对学生来说是一个非常困难的地方，TI图形计算器的游标功能恰恰可以帮助我们解决这一问题，我们可以通过移动游标，实现实时的图象变化，学生一边操作一边观察，使问题更加直观。

（一）学生操作过程

1.新建文档并添加函数图形：y=a sin(wx+t)；

2.利用“菜单－动作－插入游标”功能定义3个游标a,w,t；

3.得到初始化的函数图象（如图2）y=sinx；

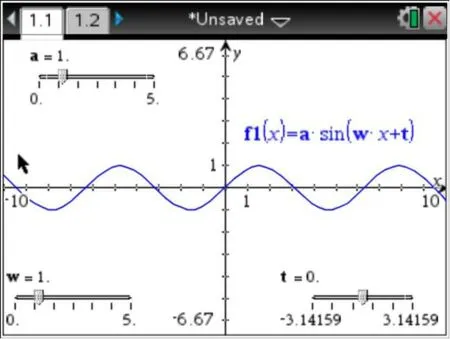
图2

4.通过分别拖动三个游标，让学生直观感受三个变量a,w,t对函数图象的影响（如图3）。

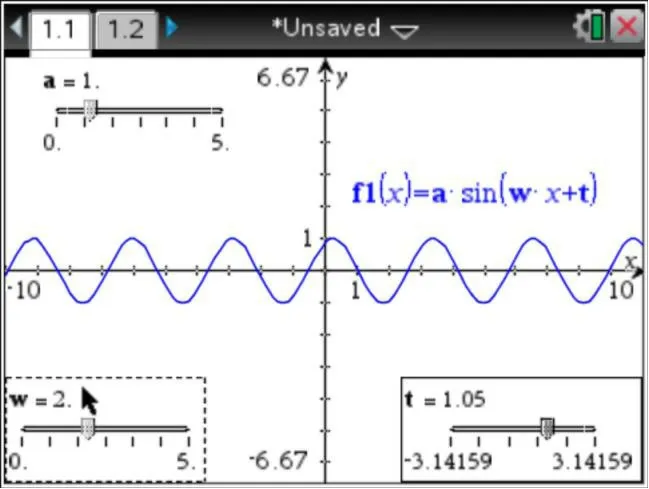
图3

设计意图：学生的亲身操作，能够让学生充分感受知识的形成过程，强化学生借助几何图形理解问题的意识。

（二）教师引导过程

在电脑平台上连接一个绘图较好的学生的图形计算器，并展示出来。1.拖动游标使a=1,w=1,t=0，记录下函数y=sinx的痕迹，再拖动游标绘制出y=sin2x的图象，引导学生观察函数图象的变化（横坐标缩短为原来的）；导学生观察函数图象的变化（向左平移?）；

设计意图：直观想象最直接的体现就是数形结合的思想。在数学探究教学中，首先要将数学问题转化成图象的形式表达出来，这样不但可以加深学生对问题的理解，还可以增强学生对教学内容的兴趣。教师通过对图象的分析，引导学生从图象向问题过渡，充分暴露知识的形成过程，根据实际情况设置疑问，让学生思考并寻求解决方法，实现直观想象素养的培养。

（三）教师设疑过程

2.让学生观察老师所画出的图象和自己的图象的区别；

3.让学生回顾思考老师的作图步骤与自己的作图步骤的区别；

4.得出结论：“先平移后伸缩”与“先伸缩后平移”会得出不一样的函数图象。

设计意图：引导学生独立思考，将难点及易错点充分展示给学生。

三、在实验教学中提升学生的数学建模素养

当实际问题需要从定量的角度分析和研究时，这就需要进行数学建模。首先，要对问题情境进行深入调查研究、作出简化假设并分析其内在规律。其次，要用数学的符号和语言来建立数学模型，再对数学模型进行求解分析。最后，利用得出的结果解决实际问题。

利用问题情境作出的简化假设有时并不直观，需要我们在多个模拟实验中，通过分析研究才能建立更优的数学模型。多个模拟实验的实施，需要对庞大的统计数据进行汇总、计算、绘图等，如果不利用现代信息技术，学生只会陷入繁琐的计算和数据处理中，失去体会知识形成过程的乐趣。借助TI图型计算器，学生可以将时间和精力集中在数学建模过程的探索和分析中，不断优化解决方案，使其数学建模素养得以培养。

案例3：函数模型的拟合实验（必修一第三章《函数的应用》P105例6）

某地区不同身高的未成年男性的体重平均值如表3-10.

身高/cm 60 70 80 90 100 110 120 130 140 150 160 170体重/kg 6.13 7.90 9.99 12.15 15.02 17.50 20.92 26.86 31.11 38.85 47.25 55.05

1.根据表3-10提供的数据，能否建立恰当的函数模型，使它能比较近似地反映这个地区未成年男性体重y kg与身高x cm的函数关系？试写出这个函数模型的解析式。

2.若体重超过相同身高男性体重平均值的1.2倍为偏胖，低于0.8倍为偏瘦，那么这个地区一名身高为175cm，体重为78kg的在校男生的体重是否正常？

实施步骤：

（一）运用TI图形计算器画出散点图（如图4）

图4

（二）拟合猜想

课本中说到，“根据点的分布特征，可考虑以y=a·bx作为刻画这个地区未成年男性的体重与身高关系的函数模型”，但实际上这个散点图并不能很清晰地看出函数模型，我们要进行函数模型的拟合猜想。

比如：这里我们选择了三个函数模型，进行分析研究。

1.二次型函数模型：y=ax2+bx+c

这样就得到一个二次型函数模型：y=0.003331x2-0.328937x+14.60369

2.指数型函数模型：y=a·bx

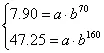
这样就得到一个指数型函数模型：y=2×1.02x

3.一次型函数模型：y=kx+b

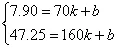
这样就得到一个一次型函数模型：y=0.44x-22.71

（三）画出三个图象，观察拟合情况，确定函数模型（如图5、6、7）。

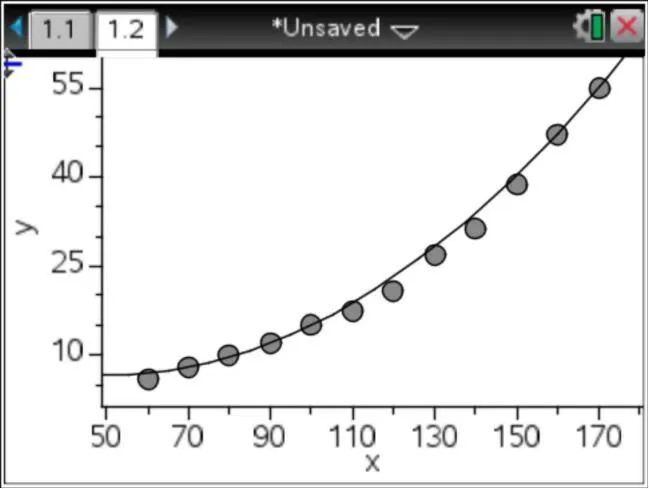
图5 二次型函数模型

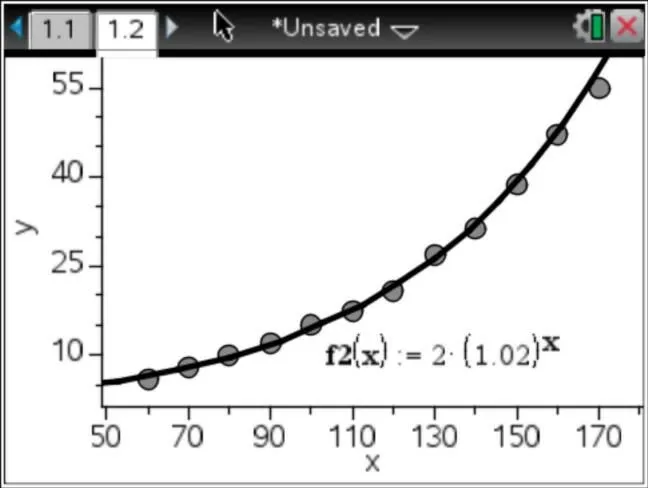
图6 指数型函数模型

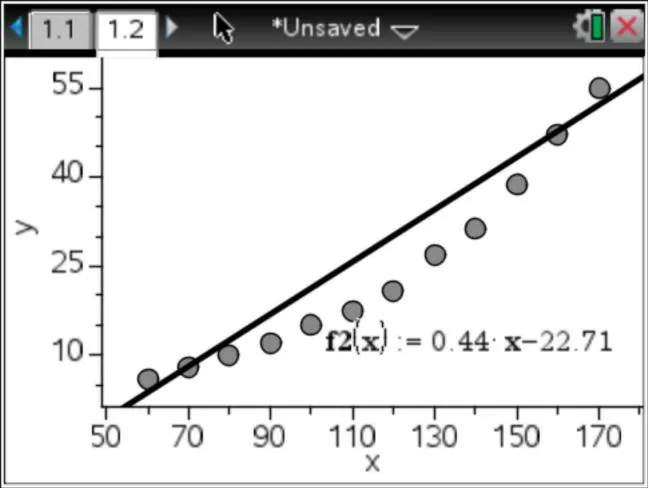
图7 一次型函数模型

从上面三个函数模型的拟合情况来看，指数型函数模型（y=a·bx）的拟合程度是最好的，因此老师可以更好地向学生讲述什么是“根据点的分布特征”来选择函数模型。但有时候单纯通过观察图像，我们无法确定哪个函数与实际数据的拟合情况更好。如果想要获得更准确的拟合曲线，可以通过选修2-3“统计案例”的学习，用“拟合函数的函数值与实际数据的误差平方和”来衡量函数的拟合程度。

在数学实验课中引入TI图形计算器不仅能够降低建模的过程中数据处理的难度，更重要的是，还可以提高学生对数学实验的兴趣，让学生体验数学建模在解决实际问题中的作用，有效培养他们的实践能力和创新意识。

数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析等组成了高中数学的核心素养。在教学中，教师应该根据不同的教学内容和课型的不同特点有所侧重，另外，数学运算和数据分析素养的提升并非一朝一夕就能实现，应该在我们平时的教学中不断渗透和加强。最后，信息技术的使用对高中数学教学有很大帮助，可帮助学生加深对知识的理解，逐步培养学生的科学研究态度和意识，它能够很好地呈现数学知识的形成过程，在培养学生直观想象、数学建模等方面都有积极的作用。因此，在积极推进我国教育现代化和信息化的背景下，倡导和探索现代信息技术辅助高中数学教学，将复杂、抽象的数学问题融入到生动的图象中，对培养学生的核心素养有重大的现实意义。