基于数字散斑方法的OGFC混合料低温变形破坏行为研究

于保阳,陈希栋,齐 琳,赵志强

(1.沈阳建筑大学交通工程学院,辽宁 沈阳 110168;2.大连海事大学交通工程学院,辽宁 大连 116026;3.沈阳城市建设学院土木工程系,辽宁 沈阳 110167)

开级配抗滑磨耗层(Open Graded Friction Course,OGFC)因排水能力强、提高路表面摩阻力、低噪音等优点被推广应用[1-2]。OGFC相比于其他类型混合料,空隙率大、粗集料含量高。但也因这种独特的结构,使其空间分布对其变形破坏行为产生很大的影响[3]。

低温变形破坏是沥青路面常见的病害,对OGFC混合料路用功能具有重要影响。多以宏观试验的名义用应力应变对材料的变形破坏行为进行整体评价[4-5]。但对材料性能的评判均基于各向同性的假定,忽视了混合料的各向异性特性[6-7]。同时忽略了破坏前的变形过程,无法得到试样表面或关注部位的变形情况。不管是试样表面还是关注部位,获得材料的实际应变场对于认知材料的宏观行为是必要的[8]。因此,综合考虑材料的各向异性进行OGFC混合料的变形破坏行为研究,对认识OGFC的力学行为与发挥路用性能具有重要意义。

数字散斑方法(Digital Speckle Method,DSM)可实现全场非接触测量。C.M.Stewart等[9]以DSM结合宏观试验发现裂纹对细观结构特征敏感;谭忆秋等[10]以DSM、应变片测量法、计算法对沥青混合料间接拉伸试验中的拉伸应变进行对比研究,表明DSM测量间接拉伸应变可行;王岚等[11]以DSM研究紫外光老化的沥青混合料裂纹产生及扩展规律,并分析了沥青混合料的界面特征。

鉴于上述分析,笔者以DSM结合四点弯曲试验对OGFC混合料的变形破坏行为开展细观研究,以便获得OGFC混合料的全场位移、应变信息,并提出应力重构,得到加载过程中的应力变化情况,进一步认识OGFC混合料的全场变形破坏行为。

1 试 验

1.1 OGFC混合料

OGFC混合料是由沥青与集料组成的开级配沥青混合料,矿粉由磨细的石灰岩制成,其级配设计如图1所示。

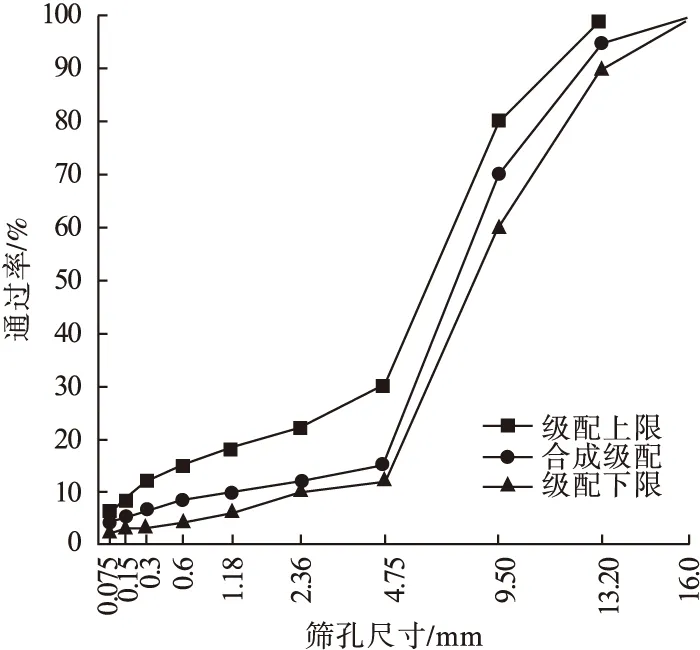
图1 OGFC沥青混合料的级配设计Fig.1 Gradation design of OGFC asphalt mixture

1.2 试验方法

1.2.1 数字散斑方法(DSM)及基本原理

笔者主要采用MatchID系统开展DSM试验,其测量装置由相机、计算机、光源构成,试验系统如图2所示。

图2 试验系统Fig.2 Test system

DSM的基本原理:对变形前后散斑图像通过相关性匹配,得到图像子区灰度场,根据像素点灰度变化进行试样位移、应变计算。其算法原理如图3所示。

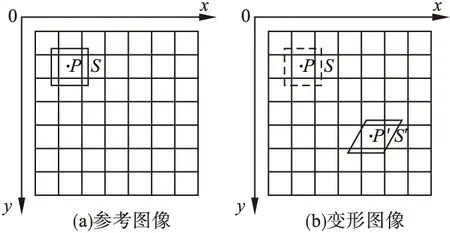
图3 相关性算法实现基本原理图Fig.3 Basic principle diagram of correlation algorithm implementation

参考图3中图像、变形图像的灰度值分别为f(x,y)、g(x′,y′),在参考图像中取一点P(x,y),并以P点为中心取大小为(2M+1)×(2M+1)像素点的子集S作为参考图像匹配子区。加载后,P点移动到P′(x′,y′)点,则S内的散斑点移动到以P′点为中心的S′子区内对应位置。基于概率统计原理,变形后的P′点可以通过与P点匹配后最大相关系数的点位置确定[12]。匹配到对应的点之后,两点坐标差即P点变形后的位移分量。

采用零均值归一化平方差和相关函数[13]计算OGFC沥青混合料梁式试件变形前后的相关系数。其中，f(x,y)为图3中参考图像点P的灰度值,g(x′,y′)为图3中变形图像点P′的灰度值;fm和gm分别为参考图像与变形图像中子区灰度平均值。

(1)

1.2.2 试件制备

将长×宽×高为300 mm×300 mm×50 mm的车辙板试件切割成长×宽×高为250 mm×30 mm×35 mm的梁式试件,并对试件制作散斑,形成白底黑斑的散斑表面,如图4所示。

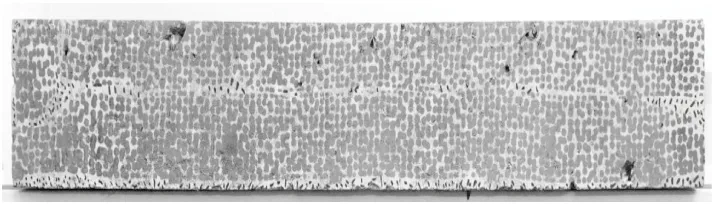
图4 试件散斑表面Fig.4 Speckle surface of the specimen

1.2.3 试验方案

试验加载装置采用SANS万能试验机,试件安放装置支座间距为L=200 mm,相邻夹头中心间距为L/3=66.67 mm,加载速率为50 mm/min,试验温度-10℃,图像采集频率为10 ms/副。

2 试验结果分析与讨论

2.1 荷载-时间曲线分析

以DSM结合四点弯曲试验研究OGFC混合料的全场变形破坏行为。其荷载-时间曲线如图5所示。

图5 四点弯曲试验荷载-时间曲线Fig.5 Load-time curve of four-point bending test

由荷载-时间曲线以及DSM分析中应变场云图演化特征,选6个代表性时间点处应变场分析其演化过程。其中,A点为试件初始加载;B点处于荷载线性增长阶段;C点位于荷载缓慢增长阶段;D点为峰值荷载附近;E点位于荷载下降阶段;F点为下降阶段末端,此时试验终止。

2.2 应变场演化分析

笔者关注OGFC沥青混合料梁式试件完全破坏前应变场的演化过程,主要通过研究其水平应变场[14]的演化来研究其变形破坏行为,如图6(a)～(f)所示。

图6 加载中水平应变场Fig.6 Horizontal strain field during the loading

由图6可知:①A点与B点的应变场无明显区别,水平应变场云图呈均匀化分布,但B点处出现了较为模糊的丝带状区域。②加载至C点,试样处于荷载缓慢增长阶段,先在右压头底部出现火苗状区域a、b,即应变集中区域,并向上扩展形成图6(c)所示应变集中带状区域,且a区域的应变集中程度高于b区域。③加载至D点,a区域的应变集中程度高于b区域,其应力也集中,当集中应力超过OGFC可承受的极限强度时,便出现图6(d)所示的a区域先于b区域开裂,同时产生裂缝尖端,其应变集中区域上移到尖端处,促进裂缝的不断扩展。④随荷载施加,a区域裂缝继续扩展,b区域处应变集中程度同步增加,当超过材料极限便出现图6(e)所示b区域开裂,同时左边压头底部由于应变的集中出现火苗状区域c;⑤加载至F点,应变集中导致左压头试件底部的裂缝开裂到一定程度,与右侧两个裂缝共同形成图6(f)中试件的最终破坏形态。

通过不同时间点不同特征的6副应变场云图的整体观察可知:随加载时间变化,初始加载时的上部水平压应变、下部水平拉应变转变为上压头之间水平压应变,其他区域以水平拉应变为主;应变场由均匀分布渐变为显著集中,表明OGFC变形的局部化特征。另外,将应变集中带与试件材料分布位置相对应,可观察到图6中a、b、c区域的应变集中带均位于较大集料之间,且所处位置的材料均是由沥青结合料与细集料形成的沥青砂浆,同时形成的裂缝也均是沿着沥青砂浆的分布,在细集料与沥青结合料的界面处开裂扩展。

2.3 应变集中带处应变特征

为更客观的定量考察应变集中带区域的演化情况,采用MatchID系统的point功能测得图6(c)中四个关注点(见图7)水平应变,其中1、3、4三点均位于应变集中带开裂点处,2点位于中间底部,其各点水平应变随采集帧数的变化如图8所示。

图7 关注点选取位置Fig.7 Selecting the locations of the interest points

由图8可知,关注点的应变变化趋势不同,在前期应变增长缓慢,没有明显差别,3、4点大约在200帧处应变增长速度加快并趋于线性,但3点增长速度在早期快于4点;1点大约在600帧处应变开始加快增长并趋于线性;1、3、4点处产生裂纹时,应变值中断;而2点由于未出现开裂,其经历1、3、4点曲线变化趋势之后趋于平稳,直到试验停止。1、3、4点根据曲线由缓慢增长到快速增长的转折处帧数可知其开裂先后次序分别是:3点、4点、1点;3点应变中断处对应时间是其起裂时间点(4.33 s),对应应变值是其起裂应变(0.014 4),进而可得到其产生开裂前(应变中断)的时间为试件变形时间段,约为0～4.33 s(520帧)。四点弯曲试验名义应变如图9所示。

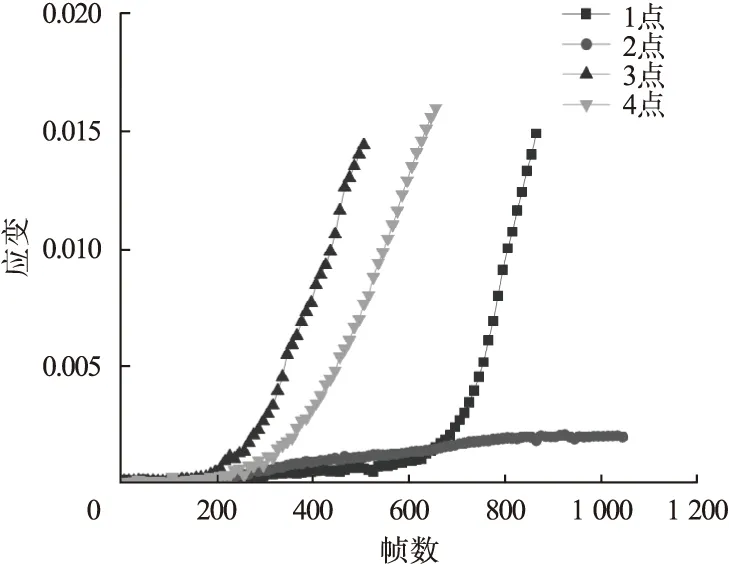
图8 关注点水平应变随采集帧数的变化Fig.8 Changes in the horizontal strain of the focus point with the number of acquisition frames

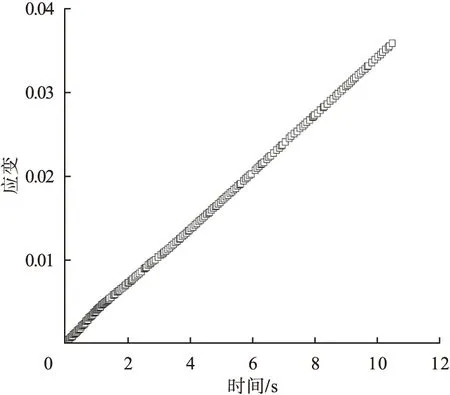
图9 四点弯曲试验名义应变Fig.9 Nominal strain of four-point bending test

对比图8与图9可知,四点应变变化趋势虽然不同,但均不是名义应变所具有的近似线性增长趋势,而是呈现出非线性增长,其原因是OGFC混合料具有各向异性,这一点也被应变场分布以及四点的应变变化得到验证,名义应变是试件均质化得到的理想应变,DSM计算的是试件表面的点的应变值。因此,由DSM分析计算得到的应变为各点的真实应变值。

2.4 OGFC混合料变形破坏过程应力重构及应力演化分析

在现有研究体系中可通过有限元[15]等方法实现应力变化研究,但有限元方法过于理想化,若能直接通过DSM获取材料应力将更具有真实性。因此笔者借鉴有限元方法,结合材料属性,通过应力-应变反演力学分析方法基于DSM的应变测量结果对OGFC沥青混合料变形过程进行应力重构。

2.4.1 应力重构

笔者所采用的四点弯曲试验处于低温情况下进行,假定其加载过程中产生弹性变形,则其变形阶段的应力-应变关系由弹性力学理论可表达为

(2)

(3)

(4)

式中:σx为水平应力;σy为垂直应力;τxy为剪切应力;μ为材料泊松比;E为弹性模量。

εx=a(σx-bσy).

(5)

εy=a(σy-bσx).

(6)

γxy=2a(1+b)τxy.

(7)

由式(5)、(6)、(7)联立反演可得到试样的水平、垂直和剪切方向的应力重构表达式:

(8)

(9)

(10)

由上述公式,结合弹性模量、泊松比以及应变数据,便可应力重构得到真实应力。其中,弹性模量、泊松比由变形阶段DSM应变计算得到。首先确定变形阶段起终点,计算试件的平均弹性模量Eav和平均泊松比μav[16]作为该阶段的弹性模量、泊松比。

为得到试件的Eav和μav,首先采用MatchID分析系统中测线(line)功能,在所得应变云图中布置测线,求取所需应变值表达式为

(11)

(12)

(13)

(14)

式中:a、b为变形阶段起终点标记;εha、εhb与εea、εeb为变形阶段起终点的平均水平应变与平均垂直应变;n为测线上测点的数目;εiha、εihb与εiea、εieb为起终点处测线测点i的水平应变与垂直应变。

根据弹性模量与泊松比定义,求解得到表达式:

(15)

(16)

式中:σa、σb分别为变形阶段起终点应力值,MPa。

2.4.2 基于DSM的应力分析

由上文可知,OGFC混合料梁式试件弹性变形时间为0～4.33 s(0～520帧),由于起点处未受力,其水平应变与垂直应变均为0,结合时间对应关系得到变形阶段终点水平应变与垂直应变。

根据试验受力状况,沿试件测面顶底边分别水平布置一条侧线计算平均水平应变,在加载端正下方分别垂直布置一条测线计算平均垂直应变。每条测线取51个点,得到试件的应变变化情况,如图10所示。图10(a)中,顶底部测线波动位于中部测点,顶部测线波动远弱于底部测线,说明试件变形发生在加载端之间,顶部为压应变,底部为拉应变且对变形起主要作用;图10(b)中,左侧测线与右侧测线平行,无显著变化,但与图10(a)相比,其垂直应变值比水平应变值小1个数量级,表明试件主要受到水平应变的作用;图10(a)与10(b)测线无规则波动以及峰值的出现,表明了OGFC混合料的各向异性特性,同时也验证了DSM对OGFC混合料的适用性。

图10 测线水平应变与垂直应变Fig.10 Horizontal strain and vertical strain of the line

将顶底部测线测点的水平应变代入式(13)中,n是两测线测点之和;将加载端正下方测线测点的垂直应变数据代入式(14)中得到:εha=0,εea=0,εhb=1.008×10-3,εeb=2.467×10-4;由时间对应确定变形阶段起终点应力值,并同上述数据代入式(15)、式(16),得:Eav=1 580 MPa,μav=0.24。

以图7中所取四点为关注点进行应力重构,将变形过程中的水平应变与垂直应变及所求弹性模量与泊松比代入式(8)、(9)中得到水平应力与垂直应力,如图11所示,其中正负值仅代表应力方向,不代表数值大小。由图11可看出，四个关注点的水平应力相比垂直应力均有大幅增长,说明试件主要受水平应力的作用。另外,水平应力值从大到小依次为3点、4点、2点、1点,其中3点的水平应力值略大于4点,并远大于1点、2点,说明3点作为先开裂点,不仅应变集中程度最高,而且应力集中程度也最高。因此,应力重构的应力分析结果与宏观现象及DSM结果一致,验证了应力重构对于分析OGFC沥青混合料应力变化规律的可行性。

图11 关注点水平应力与垂直应力Fig.11 The horizontal stress and vertical stress of the focus points

3 结 论

(1)OGFC沥青混合料四点弯曲试验时,其水平应变场在砂浆分布处出现应变集中带,直至应变集中程度最高处出现开裂。

(2)通过关注点的点应变定量分析,发现点应变呈非线性增长,前期增长缓慢,之后加快增长并趋于线性,在应变集中带处因试件开裂而中断,未开裂处后期趋于平稳。

(3)以应力-应变反演力学结合DSM的应力重构分析,验证了应力重构用于OGFC混合料应力变化规律分析的有效可行。