扭曲线路下A型地铁车辆安全性分析

侯龙刚，梁树林，池茂儒，王欢声

扭曲线路下A型地铁车辆安全性分析

侯龙刚，梁树林，池茂儒，王欢声

（西南交通大学 牵引动力国家重点实验室，四川 成都 610031）

为了研究轨道扭曲对A型地铁车辆动力性能的影响规律，本文利用多体动力学软件对标准120 km/h速度级A型地铁车辆进行动力学建模。基于多体动力学原理和轮轨接触理论，运用SIMPACK和MATLAB软件联合仿真，对不同参数下车辆临界速度和系统模态进行分析。在轨道扭曲线路条件下，对考虑不同轮轨匹配的车辆脱轨安全性进行校核；另外，为防止车辆运行中出现爬轨安全性问题，计算了轮重减载率和转向架回转阻尼系数以校核车辆爬轨安全性。计算结果表明：新轮状态下，轮轨黏着系数越高车辆运行稳定性越好，车辆参数对系统振动模态影响明显；扭曲线路工况下，车辆安全性能校核结果良好，且其校核方法为轨道车辆在此类恶劣线路下的安全性能校核提供了依据。

地铁车辆；轨道扭曲；多体动力学；SIMPACK；轮轨匹配

城市化进程和人口的不断增加，使得交通压力越来越大，道路拥挤和环境污染等问题日益突出。地铁作为地下轨道交通，与其他城市交通工具相比，有效地避免了地面交通拥堵现象，而且其运量大、方便快捷，所以地铁在城市轨道交通中的地位尤为重要。车辆的动力学性能分析是轨道车辆设计的必要环节，车辆系统动力学的研究一直以来都是轨道车辆行业的热点领域[1]。轨道线路扭曲作为常见的一种线路轨面变形工况，其形态对车辆的运行安全影响巨大。轨道线路扭曲一方面会引起轮轨作用力的变化，会影响车辆运行平稳性和舒适度；另一方面会导致同一转向架某个车轮的减载，在车轮横向力作用下，可能导致钢轨贴靠轮缘，甚至导致脱轨等行车安全事故[3]。所以有必要对车辆在轨道线路扭曲工况下车辆动力性能做一定的研究，对其在行车中的动力学指标[6]进行校核，分析轨道线路扭曲对车辆安全性能的影响规律。

1 车辆系统动力学模型和扭曲线路建模

1.1 A型地铁车辆系统动力学建模

车辆系统动力学分析方法最常用的是采用计算机对其进行数值仿真分析。为此，需要根据实际问题的需要，对车辆结构进行仔细研究，推导出其合理的运动学和动力学关系。将实际物理系统抽象成可靠的、有针对性的数学模型和多体动力学模型，期间要考虑模型的非线性环节、惯性特性和部件之间的运动关系[5]，采用数值解法对需要分析的问题进行研究。

本文在多体动力学软件SIMPACK中建立了标准120 km/h速度级A型地铁不同载荷状态下的车辆动力学模型，如图1所示。为了建立更加准确的模型对车辆动力学性能进行仿真，本文对A型地铁车辆建模时考虑了车辆横、垂两个方向运动相互耦合的动力学模型。在模型坐标系定义中采用建模时常见的坐标定义方法，即将车辆运行方向设定为轴，轴位于轨道平面内且指向车辆前进方向的右侧，轴垂直轨道平面向下。车辆前进方向第一个轮对为一位轮对。车辆动力学模型中考虑的刚体包括车体、构架、轮对和轴箱转臂结构，其质量特性如表1所示。刚体之间通过考虑非线性特性的悬挂元件相互连接传递载荷和振动，具体非线性特性曲线如图2所示。其中，一系垂向减振器、一系钢簧和轴箱转臂等一系悬挂装置将轮对与转向架连接在一起；空气弹簧、横向液压减振器、牵引拉杆和横向止挡等二系悬挂装置则连接车体与转向架。

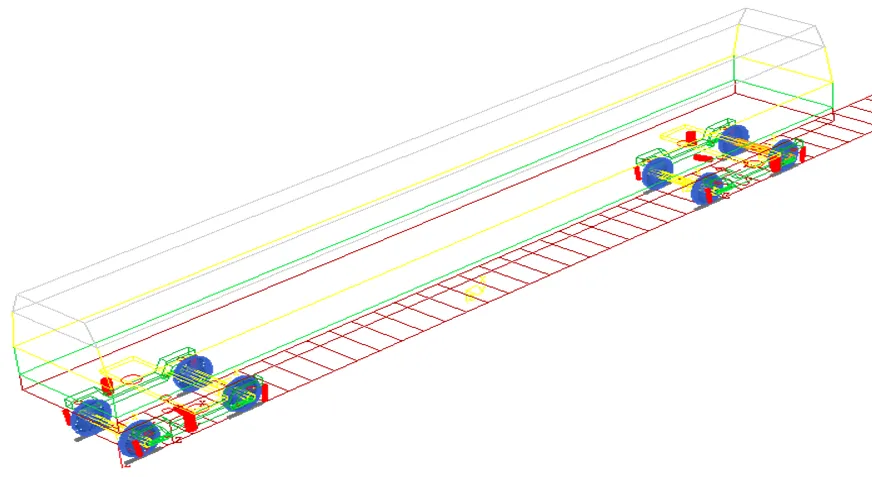
图1 车辆整车模型

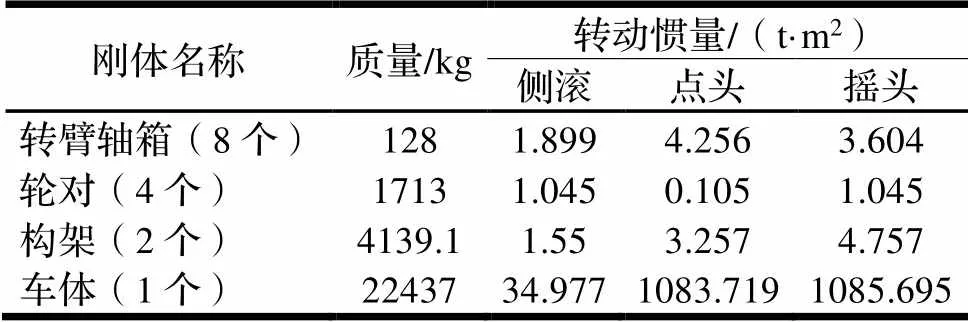
表1 多体动力学模型的质量特性

在系列化标准A型地铁车辆动力学性能研究中，轮轨接触关系是保证轨道车辆动力学计算结果合理的重要因素。在非线性轮轨关系研究中，轮轨接触几何参数被认为是轮对横移量的非线性函数，可以用轮轨横移量对其进行表征。本文中，系列化标准A型地铁车辆的车轮踏面采用LM磨耗型踏面，钢轨采用CHN60钢轨，轮对内侧距为1493 mm，轨底坡采用1:40，轨距为1435 mm。为了准确模拟系列化标准A型地铁车辆较宽泛的运行状态，更加真实的反应该车辆系统动力学性能的不同工况，分别选择LM新轮踏面与60标准钢轨匹配，来模拟车辆在新轮时的运行状态，下文称该工况为“新轮”工况；采用LM磨耗后的踏面与CHN60标准钢轨匹配，来模拟车轮踏面磨耗后等效锥度增大时的状态，下文称该工况为“磨耗轮”工况。

1.2 轨道扭曲线路建模

在不同的国家和地区中，对轨道车辆运行安全性的评价标准相差不大，但对扭曲线路条件设计的标准却各不相同[4]。本文采用欧洲标准EN 14363-2005的规定[7]，建立如图3所示的试验扭曲线路。

试验扭曲线路要求车辆运行曲线半径为150 m，扭曲线路变化梯度为3‰，线路扭曲部分位于圆曲线上，通过改变外轨的高度来实现扭曲。仿真试验时车速不得超过10 km/h，因为车速过高形成的车辆离心力会产生倾覆力矩，导致车辆外侧车轮的垂向力1增加，从而使计算的脱轨系数值降低，安全性校核结果将过于危险。

图2 减振器和横向止挡非线性特性曲线

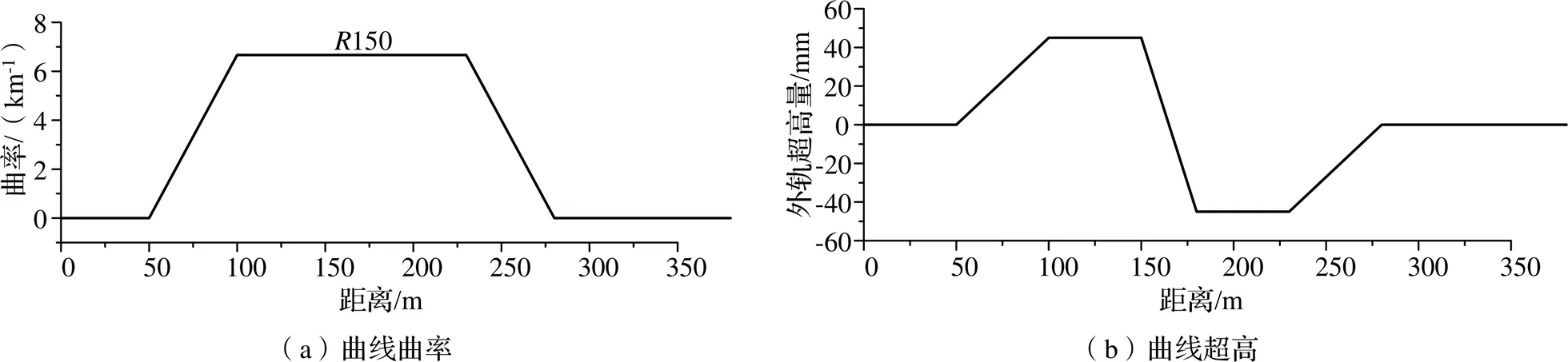
图3 仿真试验扭曲线路

2 车辆稳定性分析

2.1 不同线路黏着系数下踏面等效锥度对临界速度的影响

随着地铁交通车辆的发展，对车辆加减速，牵引和制动有了更高要求，并且运营线路条件复杂多变，为了保证车辆在运营过程中不产生空转或滑行，最大程度利用轮轨黏着，有必要对车辆在不同黏着系数下的运行稳定性进行分析计算，校核其可靠性。本节对车辆在不同线路黏着系数（0.1～0.5）下的稳定性进行了分析，计算了其临界速度，如图4所示。

可以得出以下结论：

（1）上述工况下该车辆的临界速度均高于140 km/h，满足车辆运营速度要求；

（2）随着黏着系数的降低，新轮状态下车辆的临界速度有下降趋势，对磨耗轮影响不大；

（3）新轮状态下该车辆的临界速度要高于磨耗轮的，拖车车辆的临界速度要高于动车的。

2.2 车辆参数对车辆系统模态的影响

模态是系统结构的固有振动特性，系统的每一阶模态含有其特定的固有频率、模态振型和阻尼比等。车辆稳定性分析中，除了可对车辆系统进行时域积分算非线性临界速度外，还可在无轨道激励状态下，依据车辆系统动力学方程对车辆进行线性稳定性计算，分析其根轨迹，探究车辆系统模态之间的关系。铁道车辆系统阻尼比是评价其运行稳定性的重要指标，其中，车辆蛇行模态阻尼比存在一个5%的最小阈值，一般当系统阻尼比小于5%时可认为车辆稳定性不足[8]。

图4 车辆不同状态下临界速度对比

2.2.1 车辆运动参数对系统模态的影响

对标准A型地铁车辆带动力车在空车载荷下的自振模态进行计算，以车速为变量分析了车辆运动根轨迹，图5是该地铁车辆以车速为变量的模态图谱，包括车辆系统频率随车速的变化曲线和系统阻尼比随车速的变化曲线。

由图5可以看出，车体蛇行模态频率随车辆运行速度的增加而逐渐变大，当车速在90 km/h以内时，车体蛇行模态与车体下心滚摆、摇头点头和浮沉都有耦合，但其对车辆系统稳定性影响不大，这是因为车速较小，系统阻尼比都比较大。并且在整个车速计算范围内，车辆系统的车体蛇行模态阻尼比均大于5%安全裕度，车辆稳定性较好。

2.2.2 车辆悬挂参数对系统模态的影响

根据轨道车辆系统结构特征，可知车辆一系悬挂装置对构架模态影响明显，而对车体的模态影响不大；而车辆二系悬挂更多的是影响车体的模态。故在车辆系统模态分析时，只需要考虑悬挂装置对其模态影响明显的部分进行分析。轨道车辆悬挂元件种类较多，由于篇幅限制，本节主要考虑了一系钢簧垂向刚度、转臂轴箱纵向定位刚度、空簧垂向刚度和二系横向减振器阻尼系数对车辆系统模态的影响，如图6～9所示。

图5 不同车速下车辆系统模态

图6 不同一系钢簧垂向刚度下车辆系统模态

图7 不同转臂节点纵向定位刚度下车辆系统模态

图8 不同空气弹簧垂向刚度下车辆系统模态

图9 不同二系横向减振器阻尼下车辆系统模态

由上述图6～9可知，一系钢簧垂向刚度的增加使构架的浮沉、点头与侧滚频率升高，阻尼比下降，但在整个计算范围内，其都大于5%的安全阈值，系统稳定；车体模态相对变化较小。转臂纵向定位刚度在5～23 MN/m范围变化时，其对车体模态影响不大，而构架的横移以及摇头模态频率随之增大而增大。由空簧的作用特点可知，其垂向刚度主要影响车体浮沉与点头模态，随其增加，车体浮沉、点头和上心滚摆模态频率有所升高，阻尼比降低，但在整个计算范围内仍大于5%，车辆稳定性良好。二系横向减振器阻尼系数的增大使得车体下心滚摆、上心滚摆和摇头模态阻尼比明显增大，系统稳定，上心滚摆和摇头模态频率下降。

3 扭曲线路下车辆安全性校核

3.1 车辆脱轨安全性校核

欧洲EN 14363-2005标准规定，如果轮缘角等于70°，仿真计算得到的Q1/P1值不允许超过1.2，即1/1＜1.2，这与GB/T 5599－2019所规定的脱轨系数第一限度值相同。基于此标准规定，对标准A型地铁车辆以小于10 km/h

的准静态运行速度在R150H45扭曲线路上进行仿真分析，并校核其脱轨安全性能，计算结果如表2所示。

表2 脱轨系数

由上述计算结果可知，标准A型地铁车辆在空车新轮踏面和重车磨耗轮踏面两种载荷工况下，以准静态速度通过R150H45扭曲线路时，车辆脱轨系数随车轮踏面等效锥度的增加而降低；同一工况下，拖车的脱轨系数要大于动车，这是由于拖车簧下和簧间质量较动车的小导致的；其所有工况下车辆的脱轨系数计算值都在都在标准要求的1.2限值以内，故车辆在通过此扭曲线路时，车辆不会出现脱轨安全性事故。

3.2 车辆爬轨安全性校核

在扭曲线路下，由于线路条件恶劣，车辆运行中易出现爬轨安全性事故，故需要计算运行中车辆的轮重减载率来校核车辆的爬轨安全性能。结果如图10所示。

图10 扭曲线下车辆轮重减载率

由图可以看出，在线路扭曲状态下，地铁车辆轮重减载率都在标准GB/T 5599－2019所规定的轮重减载率限度值内。车辆在不同踏面等效锥度范围内运行安全性良好，不会出现爬轨安全性事故。

3.3 转向架回转阻尼系数

轨道车辆轮重减载率的计算只涉及其在扭曲线路上车轮垂向载荷的变化。为了准确了解车辆运行中轮对横向力变化,还需计算转向架回转阻尼系数，来配合轮重减载率全面评价轨道车辆爬轨安全性。标准A型地铁车辆和扭曲线路参数如表3所示。

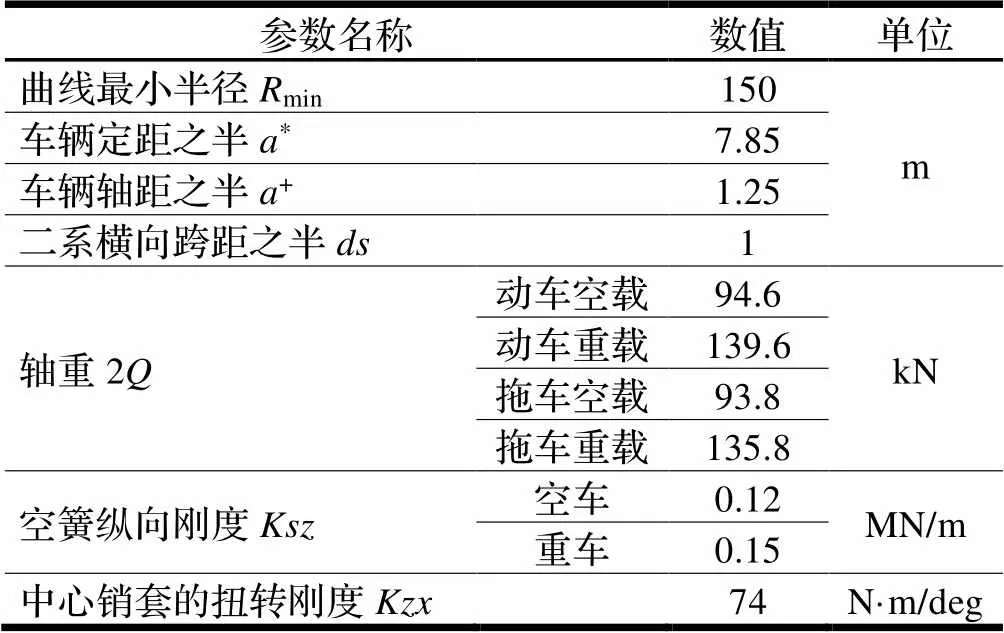
表3 车辆和扭曲线路部分参数

根据EN 14363-2005[7]规定，回转阻力系数计算公式为：

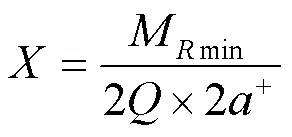
考虑到车辆运行中轮轨间隙和轨距变化，车辆通过最小半径曲线时车体相对构架最大转角可表示为：

式中：*为车辆定距之半，m；min为曲线最小半径，m。

由表3计算得最大转角＝0.0603 rad。

根据车辆通过最小曲线半径时车体与构架之间回转阻力距Mmin的具体表达式，可将式（1）转换成如下形式：

将车辆与扭曲线路参数代入式（3），计算得到转向架回转阻尼系数如表4所示。

表4 转向架回转阻力系数

由转向架回转阻尼系数计算结果可以得知，标准A型地铁车辆在R150 m扭曲线路下运行，各工况下其转向架的回转阻力系数均小于EN 14363-2005规定的0.1的限制，故车辆在该线路运行时不存在爬轨安全性问题。

4 结论

轨道车辆运行线路扭曲是导致其发生脱轨或者爬轨等安全性事故的一种重要成因。本文以标准A型地铁车辆为载体，详细阐述了轨道车辆建模理论和扭曲线路车辆安全性校核标准和原理，探明了扭曲线路车辆安全性能校核具体方法，分析了车辆稳定性和系统模态的影响规律，重点对车辆在扭曲线路下的动力性能进行了联合仿真计算，仿真计算结果如下：

（1）新轮状态下轮轨黏着系数越大，新轮车辆运行稳定性越好。但轮轨黏着系数对磨耗论稳定性影响不大。

（2）车辆运行速度在90 km/h范围内时，值得注意的是车体蛇行模态与车体下心滚摆、摇头点头和浮沉相互耦合，但由于车速较低，系统阻尼比仍比较大，故其对车辆稳定性影响不大。车速对构架固有模态影响不明显。一系悬挂参数主要影响构架的振动模态，二系悬挂参数则主要影响车体的振动模态。

（3）在扭曲线路运行时，该车型各工况下脱轨安全性系数均小于标准限制，其脱轨系数随车轮踏面等效锥度的增加而降低、拖车该指标略大于动车的结果与轨道车辆实际试验结论相符。

（4）车辆在不同踏面等效锥度范围内轮重减载率都在标准范围内，转向架回转阻力系数也均小于标准EN 14363-2005规定的0.1的限制，车辆爬轨安全性能良好。

另外，欧洲国家根据其轨道交通线路特征和维修方法，提出了线路扭曲状态下校核车辆运行脱轨和爬轨安全性的方法。建议在修订铁道车辆动力学性能评定和试验鉴定规范时，对车辆在扭曲线路下运行做出明确定义和计算标准，为我国轨道车辆仿真分析和运行安全性试验提供更可靠技术参考。

[1]翟婉明. 车辆-轨道耦合动力学[M]. 4版. 北京：科学出版社，2007．

[2]丁奥，王勇. 基于SIMPACK的铁道车辆曲线通过能力研究[J]. 机械，2019，46（4）：37-41.

[3]向俊，曾庆元. 轨道三角坑对列车脱轨安全性影响分析[J]. 长沙铁道学院学报，2001，19（1）：4-8.

[4]陆冠东，徐荣华. 线路扭曲与脱轨安全性分析方法介绍[J]. 铁道车辆，2008，46（7）：1-4.

[5]罗仁，石怀龙. 铁道车辆系统动力学及应用[M]. 成都：西南交通大学出版社，2018：116-157.

[6]国家铁路局. 机车车辆动力学性能评定和试验鉴定规范：GB/T5599－2019[S]. 北京：中国标准出版社，2019.

[7]DE-DIN. Railway applications-Testing for the acceptance of running characteristics of railway vehicles-Testing of running behavior and stationary tests：DIN EN 14363-2005[S].

[8]池茂儒，蔡吴斌，梁树林，等. 高速铁路钢轨打磨偏差对车辆动力学性能的影响[J]. 中国机械工程，2019，30（3）：261-265.

[9]周橙，池茂儒，梁树林，等. 城市轻轨低地板列车通过道岔区脱轨安全性评价研究[J]. 振动工程学报，2019，32（1）：168-175.

[10]耿烽，左言言. 铝合金地铁车辆系统动力学特性仿真[J]. 现代制造工程，2011（10）：42-46.

[11]周阳，刘晓京，李芾，等. 基于准静态试验的车辆脱轨安全性评价方法研究[J]. 铁道车辆，2014，52（5）：10-13.

[12]石田弘明，刘克鲜. 铁道车辆脱轨安全性评定标准[J]. 国外铁道车辆，1996（5）：27-34.

Safety Analysis of Type A Metro Vehicle on Twisted Line

HOU Longgang，LIANG Shulin，CHI Maoru，WANG Huansheng

(State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China)

In order to study the influence of the twisted line on the dynamic performance of Type A metro vehicle, in this paper, the multi-body dynamics software is used to model the standard 120 km/h speed class Type A metro vehicle. On the principle of multi-body dynamics and wheel-rail contact theory, the SIMPACK and MATLAB software are used for joint simulation to analyze the critical speed and system mode of the vehicle under different parameters. Under the condition of twisted line, the derailment safety of vehicles considering different wheel-rail matching is checked; in addition, in order to ensure the safety of rail climbing during vehicle operation, the wheel load reduction rate and the bogie turning damping coefficient are calculated to check the safety of rail climbing. The calculation results show that with the new wheels, the vehicle running stability gets better as the wheel-rail adhesion coefficient increases, and the vehicle parameters have a significant impact on the system vibration mode; the vehicle safety performance check result is good under the twisted line condition, and the check method provides a basis for the safety performance check of rail vehicles under the lines with severe conditions.

metro vehicles；twisted line；multi-body dynamics；SIMPACK；wheel-rail matching

U270.1

A

0.3969/j.issn.1006-0316.2021.10.006

1006-0316 (2021) 10-0038-08

2021-03-15

国家重点研发计划项目（2018YFB1201701）；科技部常规性科技援助项目（KY201701001）

侯龙刚（1996－），男，甘肃陇西人，硕士研究生，主要研究方向为车辆系统动力学，E-mail：h_kale@qq.com；梁树林（1967－），男，山西盂县人，教授级高工，主要研究方向为机车车辆动力学、车辆强度及可靠性。