基于三维Copula函数的蚀坑预测模型

喻宣瑞，姚国文，蒋一星，李乔依

（重庆交通大学 土木工程学院，重庆 400074）

在氯盐环境下，由于氯离子对拉索中钢绞线的侵蚀，使得钢绞线发生腐蚀，是索承式桥梁破坏的重要原因.考虑荷载和环境对钢绞线的耦合作用，研究钢绞线的腐蚀机制，对于延缓钢绞线的腐蚀、提高索承式桥梁在恶劣环境下服役的耐久性，具有重要的理论意义和实际工程价值［1］.

从宏观层面上看，钢绞线是由高强钢丝经过淬火、铰链等工艺制作而成，是缆索结构的重要组成部分.钢绞线的出现推动了大跨径桥梁的发展，同时也暴露出了相应的缺陷.其中一个最为致命的问题就是氯盐对钢绞线的腐蚀效应，即氯盐在潮湿环境下易与钢绞线发生电化学反应［1‑2］.

Rebak等［3］、朱劲松等［4］、Faber等［5］将钢绞线的腐蚀情况主要分为2种：吸氢腐蚀和吸氧腐蚀.在酸性环境下，易发生吸氢腐蚀；在碱性或者中性环境下，更容易发生吸氧腐蚀.Sun等［6］、Frankel等［7］、Vermaas等［8］发现，蚀坑是影响钢绞线腐蚀疲劳寿命的重要因素.在高应力作用下，蚀坑处会形成较为明显的应力集中，使钢绞线的疲劳寿命急剧下降，且下降幅度与蚀坑尺寸相关.如何精确预测蚀坑的分布规律，量化钢绞线的腐蚀寿命就显得尤为重要.为此，Tian等［9］、谢民滇等［10］从概率角度出发，假设蚀坑长度、宽度和深度之间互不影响，发现蚀坑深度服从Gumbel极值分布，并利用线性回归的方法得到了蚀坑深度与应力集中系数的关系.Valor等［11］通过机械学习法建立了马尔可夫链模型，考虑腐蚀时间和应力幅对蚀坑发展的影响，发现腐蚀时间和应力幅对蚀坑的腐蚀速率影响显著，但对蚀坑的分布规律影响较小，即可以认为不同时段下的蚀坑分布形式基本相同.

由上述研究可知，无论是物理模型试验还是具体工程案例，都表明蚀坑对钢绞线的腐蚀疲劳寿命影响显著.然而，绝大多数研究仅仅关注蚀坑深度这一单一方向，或分别考虑长度、宽度和深度对钢绞线力学性能的影响，忽视了三者之间的相互关联.蚀坑的发展是一个三维演变过程，即蚀坑深度变化的同时，其长度、宽度也会衍生，三者共同变化，应视为一个有机的整体.仅从某一方面研究其分布规律，不能客观反映蚀坑的发展规律.鉴于此，本文通过盐雾腐蚀试验来模拟钢绞线的腐蚀情况，得到蚀坑长度、宽度和深度三者的独立分布形式.并基于三维Copula函数得到其联合概率分布函数，建立三维蚀坑预测模型，同时应用Kolmogorov‑Smirnov检验（K‑S检验）等方法来验证该模型的合理性，以期为精确预测钢绞线的疲劳寿命奠定基础.

1 试验

通过YC‑200型盐雾腐蚀试验箱来模拟钢绞线的腐蚀过程，考虑荷载和环境二者的耦合作用，盐雾喷射速率为250 mL/（m2·h）.钢绞线由碳素钢混合其他金属材料制作而成，除Fe元素外，主要化学元素含量（质量分数，文中涉及的含量等除特别说明外均为质量分数或质量比）为：0.83%~0.86% C，0.62%~0.84% Mn，0.12%~0.20% Si.钢绞线由7根高强钢丝组成，直径为15.2 mm，抗拉强度为1 860 MPa，二级松弛率，单根钢绞线镀锌层质量不低于110 g/m2.钢绞线两端借助千斤顶和反力墙施加交变荷载，应力幅（Δσ）分别为100、200、300 MPa，荷载最大值为744 MPa［12］，即0.4fptk（fptk为钢绞线极限强度标准值）.拉伸试验采用WAW‑1000型万能试验机，每2 h实现钢绞线应力上下限转换，4 h为1个加载周期.

拉伸试验完成后采用KYKY‑2008B型工业电子显微镜（SEM）观测钢绞线的腐蚀形态，得到3种应力幅下的蚀坑尺寸，以便定量分析蚀坑的分布规律.

综合考虑温度、湿度等因素的影响，参考文献［13］和ASTIM G85—94《Standard practice for modified salt spray（fog）testing》，盐雾溶液由NaCl、冰醋酸、CuCl2·2H2O及蒸馏水组成，其中CuCl2·2H2O浓度为（0.26±0.02）g/L，最终浓度控制在（50±5）g/L；加入冰醋酸是为了保证盐雾溶液的pH值在3.1~3.3之间；温度设定为25℃.盐雾腐蚀试验完成后，在80℃下用铬酸溶液清洗钢绞线.为防止残留氯离子对钢绞线的腐蚀，可采用AgNO3溶液进行中和，再用自来水冲洗，冷风吹干静置.

2 结果与分析

腐蚀时间和应力幅是影响钢绞线力学性能的重要因素.为探究腐蚀时间对钢绞线力学性能的影响，以应力幅Δσ=200 MPa为例，分别在盐雾腐蚀试验进行120、360、600、720 h时，测量钢绞线的抗拉强度（fT）和延伸率（A）.将钢绞线进行切割，每段长约1 m.考虑到扩张力会对夹持在钢绞线上的引伸计造成损坏，本试验不采用夹持引伸计进行测量，而是用油缸位移代替引伸计伸长量.在预加载阶段，采用2 mm/min的速率，达到目标荷载2 kN后，采用1 kN/s的加载速率进行定向拉伸，直至破断.6根钢绞线部分时段的静态拉伸曲线如图1所示.由图1可见，随着钢绞线在盐雾环境中暴露时间的延长，其抗拉强度出现了明显下降.

图1 钢绞线的应力-应变曲线Fig.1 Stress‑strain curves of steel strands

钢绞线的腐蚀特征参数如表1所示.由表1可见：（1）当盐雾腐蚀试验进行到70 h时，钢丝由于镀锌层的保护，几乎未被腐蚀.钢绞线两端施加荷载约28 kN时，钢绞线的抗拉强度为1 850~1 890 MPa，延伸率（包括钢绞线的弹性变形）大于5.5%.（2）当盐雾腐蚀试验进行到120 h时，钢丝镀锌层腐蚀，出现大量白锈，同时有极少量红锈出现，腐蚀失重为10~150 g/m2，钢绞线的基体开始出现腐蚀.当荷载加载至27 kN时，其抗拉强度为1 710~1 860 MPa，延伸率为5.0%~5.5%.（3）当盐雾腐蚀试验进行到360 h时，钢丝出现大量红锈，去除腐蚀产物后可见少量蚀坑，腐蚀失重为150~300 g/m2.钢绞线两端施加荷载为25 kN时，其抗拉强度和延伸率开始出现明显下降.（4）当盐雾腐蚀试验进行到600 h时，钢丝出现较多锈蚀或损坏，部分截面出现削弱，去除腐蚀产物后可见密集蚀坑，腐蚀失重为300~400 g/m2.钢绞线两端施加荷载为21 kN时，其抗拉强度为1 350~1 550 MPa，延 伸 率 为3.2%~4.2%.（5）当盐雾腐蚀试验进行到720 h时，钢丝出现大量严重锈蚀，钢绞线两端施加荷载为19 kN时，肉眼可见锈蚀空洞，小蚀坑之间相互贯穿形成较大蚀坑.去除腐蚀产物后可见大面积蚀坑，截面严重削弱，刮取少量腐蚀产物溶解于盐酸溶液中，再滴入KSCN溶液，发现溶液呈现血红色（Fe（SCN）3），说明该腐蚀产物含有大量Fe3+.

表1 钢绞线腐蚀特征参数Table 1 Corrosion parameters of steel strand

为直观反映应力幅对钢绞线腐蚀程度的影响，在盐雾腐蚀试验进行到720 h时将试件取出，通过SEM来观察钢绞线的腐蚀形态，结果如图2所示.由图2可见：应力幅为100 MPa时，钢绞线表面较为平整，蚀坑深度较小，密度较大，个别蚀坑直径约为40μm，部分镀锌层仍在；应力幅为200 MPa时，钢绞线表面出现大量蚀坑，且蚀坑深度明显比应力幅为100 MPa时大，个别蚀坑直径约为55μm，部分蚀坑已联合贯通，形成裂纹；应力幅为300 MPa时，钢绞线表面出现大面积腐蚀，镀锌层已经被完全破坏，大量小蚀坑已联合贯通形成较大蚀坑，个别蚀坑的直径约为75μm，蚀坑位置处产生明显裂纹，部分裂纹已经开始衍生，钢绞线寿命将受到严重影响.

图2 钢绞线的腐蚀形态Fig.2 Corrosion patterns of steel strand

3 蚀坑的分布规律

通过Valor等［11］的研究发现，应力幅和腐蚀时间对蚀坑的分布形式不会产生显著的影响，即在不同应力幅和不同时段下，蚀坑分布规律具有统一性.为便于测量蚀坑的尺寸，待盐雾腐蚀试验结束后（即盐雾腐蚀试验进行720 h），对所有试件表面的蚀坑尺寸进行统计.蚀坑的宽度、长度可采用SEM进行标记，如图3所示.蚀坑深度可采用Bruker台阶仪进行测量，具体可参照文献［14］.分别采用不同的分布形式对蚀坑的长度、宽度、深度进行分析，并利用K‑S检验，得到各种分布的误差值（D），残差值（RMSE）和赤城信号值（CAI），将各分布模型检验结果汇于表2.

图3 蚀坑的散点分布Fig.3 Distribution of scattered points of erosion pit

由表2可见，蚀坑长度和深度的分布形式更符合Gumbel极值分布，宽度的分布形式更符合对数正态分布.图4为概率模型的参数分布.

图4 概率模型的参数分布Fig.4 Parameter distribution of probability model

表2 检验参数表Table 2 Inspection parameters

Copula函数是不限定变量的边际分布函数，通过Copula函数可以将任意K个独立分布的边际函数联系起来，得到一个多变量联合概率分布模型，能够更为客观地反映蚀坑分布规律.

4 三维Copula函数理论

迄今为止，Copula函数种类繁多，其主要类型大致分为3种：椭圆型、阿基米德族和二次型.其中，阿基米德族Copula函数结构简单，计算简便，可以构造出形式多样、适应性强的多变量联合分布函数，在实际中应用较多.阿基米德族Copula函数族是通过算子ϕ（又称生成函数，一个完全单调的函数）构造而成［15］，n维阿基米德族Copula函数定义如下：

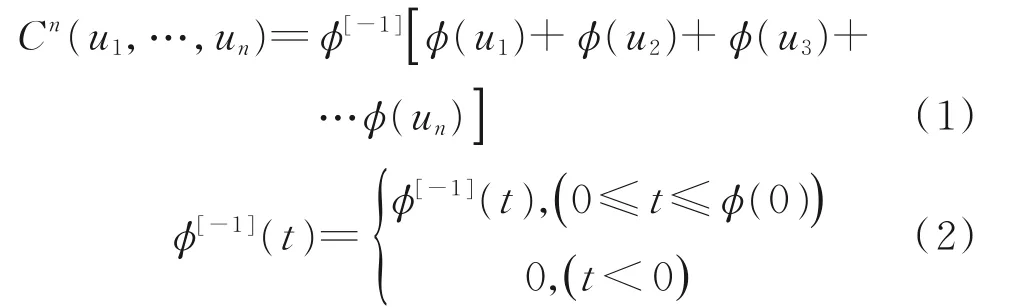
本文以三维随机变量为例，当n=3时，其表达式为：

式中：C(u1，u2，u3)为多维Copula函数，表示随机变量X1，X2，X3…Xn之 间 的 关 系ui=F(Xi)；i=(1，2，3，…，n)，表示单个随机变量概率分布函数；ϕ是一个连续、严格的递减凸函数，满足ϕ(0)=+∞，ϕ(1)=0；ϕ-1(1)为ϕ的逆函数，仍为一个单调递减，且 连 续 的 反 函 数，满 足ϕ-1(∞)=0，ϕ-1(0)=1.Copula函数的具体证明过程可参考文献［16］.

4.1 Copula函数

从式（1）、（3）中不难看出，通过求解算子式，进而可知Copula函数相应表达形式，不同算子式对应不同Copula函数.下面介绍几种常见的Copula函数：

称为Frank Copula：

（2）算子式ϕθ(t)=(-lnt)θ的Copula函数称为 Gumbel‑Hougard Copula：

（3）算子式ϕθ(t)=t-θ-1的Copula函数称为 Clayton Copula：

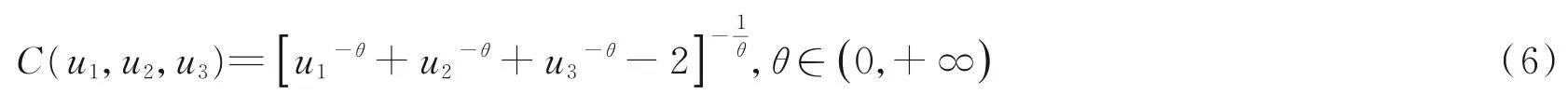
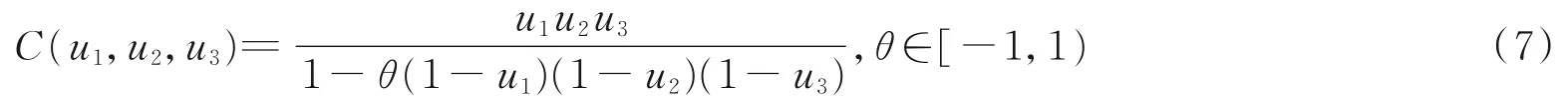
4.2 参数估计

采用参数估计法中的IFM法（极大似然法）对θ值进行求解［15］，该过程由以下2步完成：

（1）采用IFM法估计边际分布中的参数a1、a2、a3.

（2）采用IFM方法估计Copula中的参数θ.

4.3 Copula函数运用流程

（1）确定各参数适合的分布形式，通过K‑S检验、均方根误差等方式找到各参数的独立分布形式.

（2）判断各参数之间的相关性，通过IFM方法确定适宜的Copula函数，明确Copula函数具体形式.

（3）通过拟合优度检验，从众多Copula函数模型中确定出最为合理的Copula函数.

5 检验分析

各种Copula函数模型的线性相关性检验结果如表3所示.其中R为Pearson古典相关系数，S为Spearman相关系数，τ为Kendall’s秩相关系数.由表3可见，长度与宽度的相关性较高，而长度与深度、宽度与深度的相关性较低.根据阿基米德族Copula函数的结构特征，Clayton、Franck和Gumbel函数对线性相关检验结果更为适合.对这3种函数做优度检验，得到其RMSE、CAI、D和θ值，如表4所示.由表4可见，Clayton Copula函数的RMSE、D和CAI值最小，对样本的拟合效果最佳.

表3 线性相关系数Table 3 Linear correlation coefficient

表4 优度检验参数Table 4 Goodness test parameters

将Clayton Copula函数计算结果与经验公式（式（10））计算结果作对比，结果如图5所示，图中的散点值为Clayton Copula函数计算结果.由图5可见，各散点值都均匀分布在y=x这条斜线的两侧，在一定程度上说明了Clayton Copula函数计算结果的精确性.

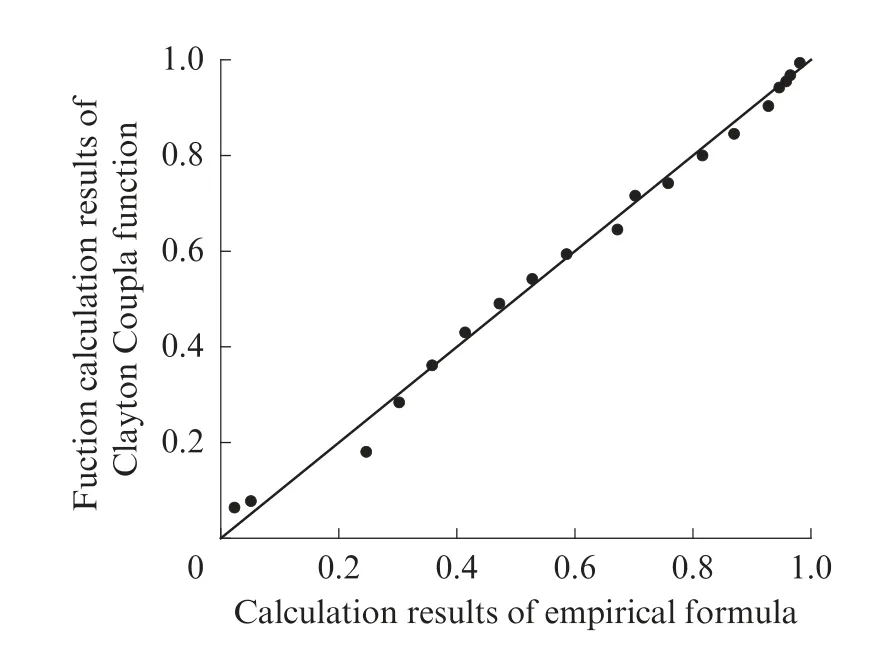
图5 Clayton Copula函数计算值与经验公式计算值对比Fig.5 Comparison between the calculated value of Clayton Copula function and the calculated value of empirical formula

式中：X为蚀坑长度，mm；Y为蚀坑宽度，mm；Z为蚀坑深度，mm.

为直观反映蚀坑的三维预测结果，用xi，yi，zi这3个变量来描述蚀坑的长度、宽度、深度，得到当[P(xi,yi,zi)=P(X≤xi)=75%P(xi,yi,zi)=P(Y≤yi)=75%]时的各联合概率分布，如图6所示.从图6中可以较为直观地看出蚀坑长度、宽度和深度的分布规律，能够较为精确地预测不同蚀坑尺寸发生的概率，为预测钢绞线的腐蚀疲劳寿命提供参考.

图6 条件联合概率分布值Fig.6 Conditional joint probability distribution

6 结论

（1）蚀坑长度和深度的分布形式符合Gumbel极值分布，宽度的分布形式符合对数正态分布.

（2）Clayton Copula函数对实测数据的拟合效果最佳，其精度较经验公式更高.

（3）蚀坑三维预测模型的建立，可以更为客观地反映蚀坑长度、宽度和深度的变化规律，大致预测不同蚀坑尺寸发生的概率，为进一步探究钢绞线的腐蚀疲劳寿命提供参考.