基于FSST和D-K聚类的次同步振荡分析

阳育德，莫富钧，卢建洛，覃智君

(1.广西大学 电气工程学院， 广西 南宁 530004；2.广西电力系统最优化与节能技术重点实验室， 广西 南宁 530004)

0 引言

近年中国风电并网规模继续增加，截止2020年6月底，全国风电装机累计达到2.17亿千瓦，上半年风电发电量2 379亿千瓦时，同比增长10.9%[1]，光伏发电量1 278亿千瓦时，同比增长20%[2]。然而，随着风光电等新能源普及率的提高，多源多变换的发杂交直流系统的形成使得次同步振荡(subsynchronous oscillation, SSO)更加频繁，危及电网的安全稳定运行[3- 4]。近年来，基于同步相量测量单元的广域测量系统在电力系统中获得了广泛应用[5]，为次同步分析提供了数据来源，因此基于实测数据的信号分析法成为模态辨识的主要思路[6]。

当电力系统中发生次同步振荡现象时，量测到的SSO信号是一种典型的非平稳时变信号。通过实测信号分析研究次同步振荡问题是电力系统的重要内容之一[7]。现有的基于信号分析的模态辨识方法主要有Prony分析[8-9]、希尔伯特-黄变换[10](hibert-huang transform, HHT)等。Prony分析法可分析确定性振荡信号，能够准确得到信号的幅值、频率、相位和衰减因子等信息[11]。Prony算法对随机信号的分析结果精度差，且对噪声十分敏感，抗噪能力不够理想[12]。HHT能对随机振荡信号进行处理，得到信号频率和幅值随时间变化的关系[13]。但如果信号中存在频率比值小于1.5的两个振荡分量时，HHT分析会发生频率混叠现象[14-15]，不适用于多振荡模态存在的电力系统，且HHT存在端点效应，边界处的频率和幅值辨识误差较大[16-17]。

DAUBECHIES等提出了一种新的基于同步挤压小波变换(synchrosqueezed wavelet transform, SWT)的时频分析方法[18]，SWT具有良好的模态分解能力和抗噪声能力[19-20]，但SWT利用连续小波变换同步挤压处理时，应选择合适的小波母函数，不同的小波母函数同步挤压效果相差很大[21-22]。2014年，OBERLIN等提出以短时傅里叶变换基础的傅立叶同步挤压变换(fourier-based synchrosqueezing transform, FSST)[23]。文献[24]采用同步挤压变换 (synchrosqueezing transform，SST)对系统低频振荡模态进行参数提取，证明SST比经验模态分解(empirical modal decomposition, EMD)抗混叠能力更强，与希尔伯特变换(hilbert transform, HT)结合，获取的低频振荡参数准确度高于HHT方法。文献[25]对SSO信号进行了SST时频分析，选取振荡模态重构信号，通过参数辨识获得较高精度的频率辨识结果，但该方法要通过观察图形获得时频谱上的振荡模态频率，无法直接从时频谱分析中获取振荡模态频率。文献[26]将FSST首次引入间谐波的检测分析，并结合Hilbert变换进行参数辨识，在FSST的基础上加入调制因子使其能获得更准确的振荡频率。但间谐波与次同步振荡信号模型不同，需辨识的参数亦有增加，且文献指出FSST存在无法事先确定模态分解层数的问题。因此本文提出了改进方法，并应用于次同步振荡信号分析中。

本文提出将FSST应用于电力系统次同步振荡信号检测分析和参数辨识的方法。利用FSST较强的抗混叠和抗噪性，对含有多重振荡模态的次同步振荡信号进行模态分离。分离后重构信号的振荡模态，对重构的振荡模态进行参数辨识得到反映振荡模态特征和发展趋势的信号参数。同时运用具有噪声的基于密度聚类(density based spatial clustering of applications with noise, DBSCAN)和K均值(Kmeans)聚类的混合聚类对FSST算法进行改进，使其能自适应识别振荡信号中的振荡模态数量以及振荡模态频率，精确定位振荡模态所在的频带进行重构，提高了FSST分析方法的便捷性。通过仿真算例，证明本章所提分析方法的可行性和优越性。

1 FSST方法

FSST方法基于短时傅里叶变换(short time fourier transform, STFT)方法，STFT是一种对傅里叶变换进行加窗处理的变换方法，以能提高傅里叶分析在时域局部表达上的局部定位能力。假设存在信号f(t)，则将其傅里叶变换表达式为

则STFT表达式为

式中,g为窗函数。

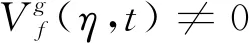
(1)

式中,Re(·)指取其实部。

(2)

式中,γ为阈值；δ为狄拉克分布。

重构f(t)第k个分量为

(3)

2 结合D-K聚类的次同步振荡SST检测方法

2.1 Kmeans聚类原理

Kmeans聚类算法是一种基于划分的硬聚类算法[27]。该算法采用距离衡量样本间的相似性，能将样本集x1,x2,…,xn划分为人为设置的k个簇，簇Ci的均值向量为该簇的质心μi，即

Kmeans算法的目的是寻找k个质心，以获得最小化平方误差E。平方误差E越小，则簇内样本的相似度越高。平方误差E可表示为

Kmeans算法过程如下：

① 从样本集X={x1,x2,…,xn}中，随机选择k个样本{μ1,μ2,…,μk}作为初始质心；

② 计算其他样本xi与质心μj间的距离，将所有样本与离它最近的质心归为一个集合；

③ 把所有样本归好集合，重新计算每个集合的质心。如果重新计算得到的质心和初始质心距离满足平方误差E小于设置的阈值，即认为算法按期望把样本集分成k个簇，聚类目标完成，否则将计算得到的质心重新代入从②进行聚类直到条件满足为止。

2.2 D-K聚类原理

DBSCAN算法是一种基于密度的算法，对比划分聚类算法和层次聚类算法有很大的优势：其对任意形状的簇都能进行识别和分析，并且可以有效地识别数据集中的噪声点。Ep和Psmin是聚类算法需要引入的2个参数，其中Ep为聚类类簇的半径，Psmin为每个类簇中的最小样本数目。Ep近邻：数据集D中某点p的Ep近邻是指在其领域半径Ep范围内点的集合，记为Ep(p)，Ep(p)被定义为

Ep(p)={q∈D|distance(p,q)≤Ep}。

噪声点:假设C1,C2,…,Ck为数据集D根据参数Ep和Psmin产生的k个类簇，如果数据集D中某些点不属于其中任何一个类，那么这些点就被定义为噪声点，表示:

noise={p∈D|∀i:p∉Ci},i=1,2,…,k。

DBSCAN算法的过程如下：

① 在数据集D中随机选取一个点，把该点的Ep近邻都归为一个簇；

② 选取这些点再找出它们的Ep近邻，直到被归为一个簇的点再也找不到新的Eps近邻为止是；

③ 选取该簇以外的任意点重复上述过程，直到样本中的所有点都被归类为簇或者噪声点为止。

由于Kmeans聚类算法需要事先人为确定聚类的簇的数量，依据此数量进行类簇划分从而计算出类簇的质心；而DBSCAN聚类算法无需事先确定簇的数量，通过运算将数据划分为k个类簇，但无法计算得出簇的质心。

因此提出将两种聚类算法结合的D-K混合聚类的方法，首先运用DBSCAN算法将数据划分成类簇并得出类簇数量和类簇集，再通过Kmeans聚类计算出DBSCAN算法划分得到的每个类簇的质心，可在无需人工干预的情况下自动分类处理目标数据。将此混合聚类方法应用于次同步振荡信号的FSST分析中，达到自动识别信号所含振荡模态数量和定位模态振荡频率的目的。

2.3 D-K聚类结合FSST方法

采用D-K聚类结合FSST方法对含有次同步振荡分量的电力系统信号进行分析的主要步骤分为以下几步：

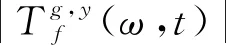
④ 由步骤③中所得振荡模态频率ωfn来选择频率区间，经过式(3)进行重构，得到k个次同步振荡模态分量。

⑤ 对重构得到的次同步振荡模态分量进行Hilbert变换，提取次同步振荡模态分量信号的参数。

3 数值仿真分析

3.1 模拟SSO信号算例分析

引入一组典型的模拟SSO信号s(t)，其表达式如下：

s(t)=3e-0.03tcos(27πt+30°)+8e-0.4tcos(40πt+45°)+4e0.3tcos(57πt+60°)+5e0.02tcos(70πt+30°)。

模拟SSO信号的仿真时间为5 s，采样频率为500 Hz。图1所示为模拟SSO信号的时域、频域特性图，在理想无噪声的情况下，信号的时域图如图1(a)所示。对模拟SSO信号进行快速傅里叶变换(fast fourier transformation, FFT)频谱分析作为参考，结果如图1(b)所示，由图1可知该信号存在4个次同步振荡频率分量。

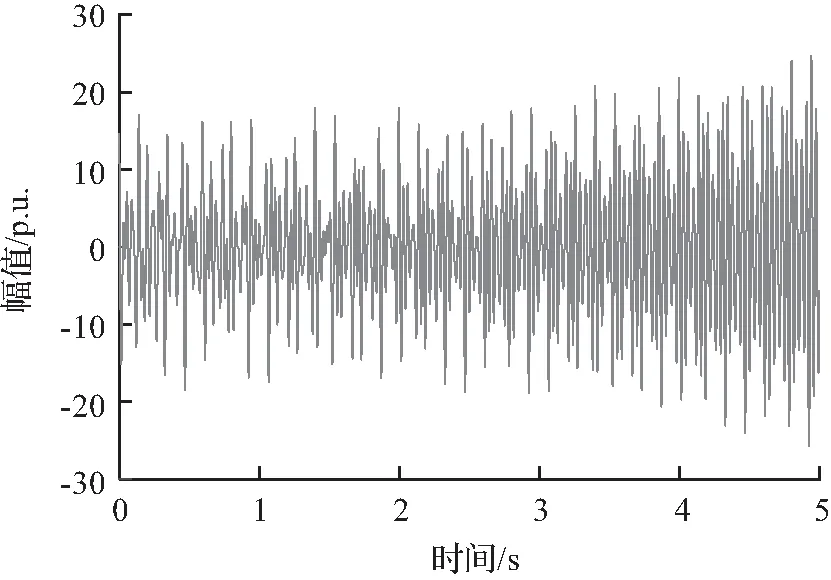
(a) 模拟SSO信号的时域图

FFT一般用于频率和幅值不变的信号分析，虽然通过FFT频谱分析，能够得到信号所包含的次同步振荡分量振荡频率，但无法表达某一频段的振荡分量的时域信息。而电力系统中的次同步振荡信号的幅值和频率大多是时变的，因此FFT在对次同步振荡信号分析中存在局限性。因此本文提出采用FSST和SWT方法对此模拟信号进行总体时频分析，时频分析结果如图2所示。

所得信号FSST总体时频分析结果如图2(a)所示。在这个模拟信号算例的分析过程中，还将对比FSST方法与经典的EMD、SWT算法的分析结果。文献[18]、文献[28]分别展示了EMD、SWT算法的主要流程。从时频分析结果图可以直观地观察到该模拟SSO信号中包含4条的时频曲线，其代表4个振荡频率，分别在13.5、20、28.5、35 Hz左右，与FFT频谱分析的结论一致。同时可以观察出，频率为28.5 Hz和35Hz的时频曲线亮度随时间增加，表示其振荡模态的模态能量随时间逐渐增加，尤其是28.5 Hz左右处的振荡模态的能量增大比较明显，意味着此振荡模态有不断增大发散的可能。相反，频率为13.5 Hz与20 Hz左右处的振荡模态的模态能量随时间逐渐减小，尤其是20 Hz左右处的振荡模态的能量减弱较明显。

图2(b)为SWT的总体时频分析结果，设置SWT 的小波基函数σB值为12。通过时频图可以看出，SWT和FSST均能得到 4 条振荡模态的时频曲线，代表4个振荡模态。其中SWT在振荡频率为28.5 Hz和32 Hz的两个模态的时频曲线出现了轻微的混叠现象；而FSST的时频曲线精细清晰，清楚地展示了信号中4个振荡模态的能量变化趋势。说明在含噪声的场景中，FSST仍具有较高的抗模态混叠性能，能成功分辨距离较近的模态。

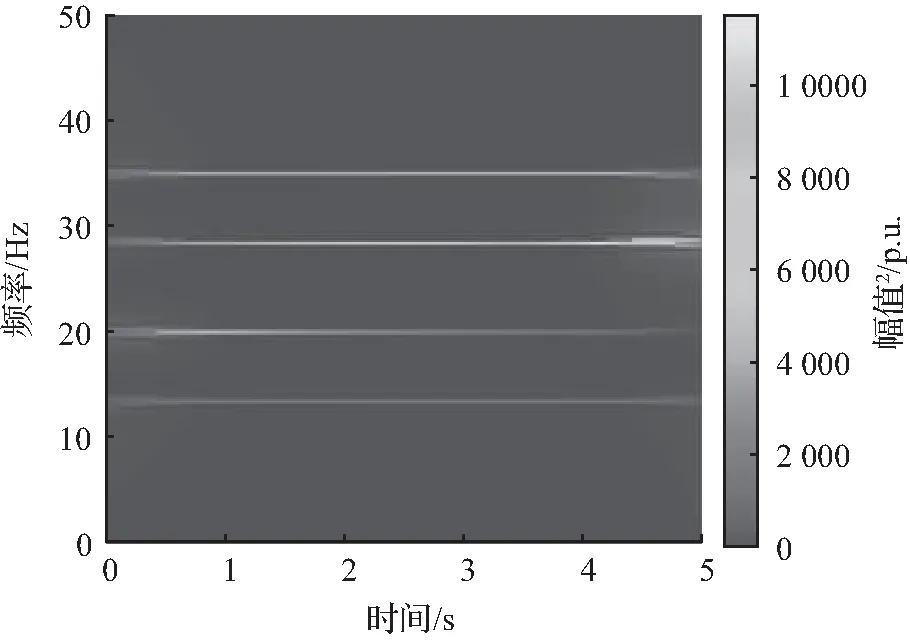
(a) FSST时频分析结果

采用FSST反变换对信号进行完全重构，得到结果如图3所示。图3(a)中实线曲线为原始模拟SSO信号，虚线曲线为FSST重构信号。从重构结果可以看出，FSST的重构信号曲线基本覆盖原始信号，幅值大小一致，重构后的相对误差如图3(b)所示，相对误差都处于非常小的数量级，说明FSST方法对信号的重构精度较高。

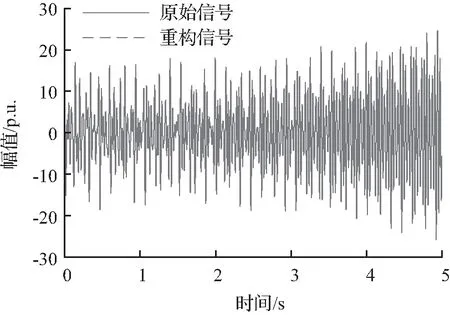
(a) 原始信号与重构信号对比图

图4为FSST同步挤压变换量矩阵中的同步挤压变换值经D-K混合聚类后的结果。设置阈值为最大同步挤压变换值的10%，消除FSST底噪使聚类算法效果更佳。由图4可知，得益于FSST的良好挤压效果，DBSCAN算法将同步挤压变换值准确地划分并识别到4个明显的簇。每个簇内的同步挤压变换值聚集在某个频率周围，意味着在此频率下存在着一个振荡模态。再通过Kmeans算法计算簇的质心，即得到振荡模态频率。表1为D-K混合聚类后得到振荡模态频率结果，可以看到聚类得到了准确的模态数量和精确度较高的模态振荡频率。表明通过D-K混合聚类可以从信号经FSST后得到的时频图中直接将振荡模态的频率信息提取出来，具有极大的便利性。

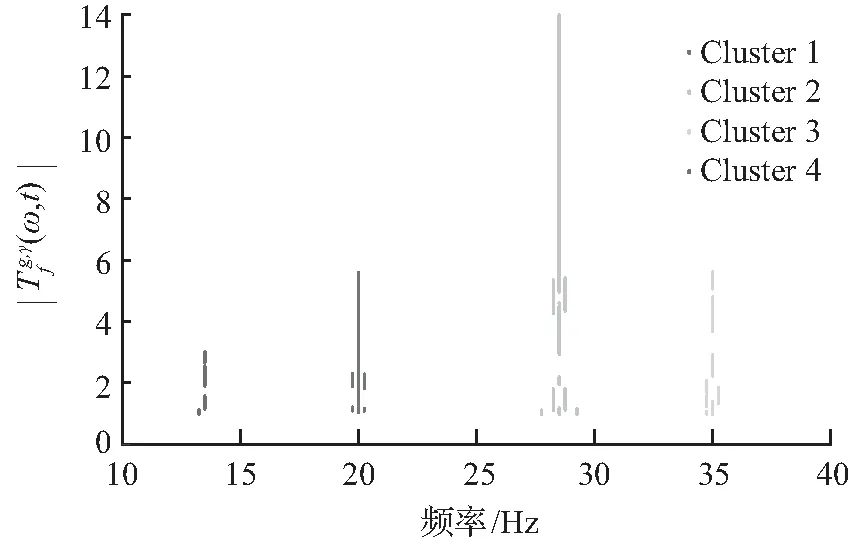
图4 D-K聚类提取振荡频率结果

表1 振荡模态频率的聚类结果

FSST能够将信号包含的频率分量从信号中分离并进行重构。根据FSST总体时频分析所得的结论，对振荡频率采用式(3)进行振荡模态的信号重构，图5为FSST振荡模态分解结果。记信号分量IMT1-IMT4分别为13.5、20、28.5、35 Hz频率分量的振荡模态信号重构结果。图6为SWT法的模态分解结果，分解得到4个振荡模态。图7为EMD法的部分模态分解结果。

图5 FSST模态分解结果

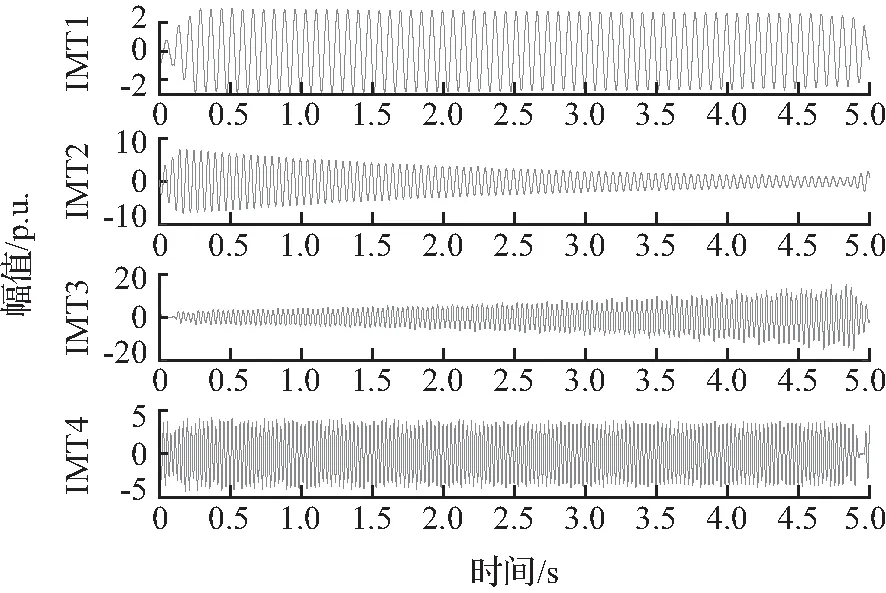
图6 SWT模态分解结果

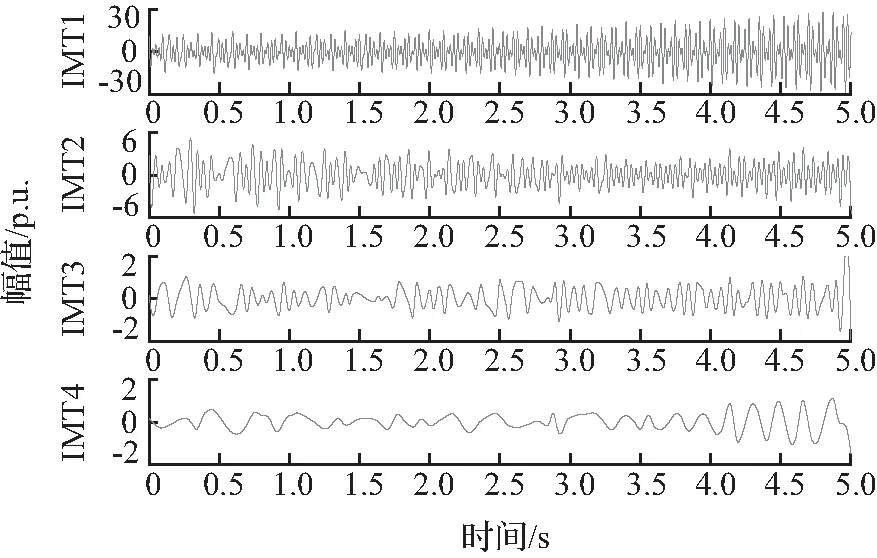
图7 EMD模态分解结果

经验模态分解方法EMD分解得到8项信号分量IMF，图8展示了前4项。其中，第一项IMF1近似于原始信号，第四项IMF4可被误认为低频扰动成分。图9为EMD前两项模态分量IMF1和IMF2的FFT频谱分析结果。

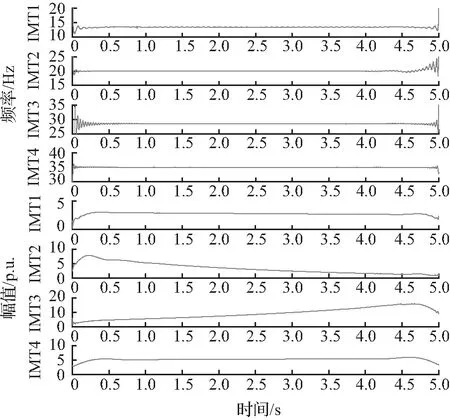
图8 经FSST得到的各分量的瞬时幅值和瞬时频率

(a) IMF1的频谱分析结果

可以看到分量IMF1包含了与原始信号相同的4种频率成分，而IMF2的6种频率成分仅包括原始信号中的2种。由此可见，对次同步振荡信号进行EMD分解时出现了模态混叠现象，EMD无法将信号中所含各振荡模态分量从原始信号中分离出来并还原。这种模态混叠现象不仅会导致振荡模态数量的误判，引入虚假分量，而且对各模态分量的还原度较低，使得利用HHT进行模态参数辨识时无法得到较为准确的模态分量参数。而结合D-K聚类分析的FSST能准确判断振荡模态数量，定位振荡模态所处频率进行信号重构。在图4中，FSST则克服了模态混叠问题，重构之后得到与原始信号吻合度较高的各振荡模态分量，避免模态混叠后分量失去其物理意义而造成信号分析参数辨识上的错误。

由图9可以看出，FSST重构之后的模态分量瞬时频率在端点处的波动较大，除端点外的频率与原信号频率基本吻合。信号端点重构精度问题主要是因为FSST和Hilbert变换都存在端点效应。通过求取平均值的方法获得振荡模态分量的频率参数，再通过最小二乘法拟合瞬时幅值曲线求得模态分量幅值和衰减因子。

将FSST分解所得的振荡模态，经Hilbert变换后进行参数辨识结果见表2，与SWT的辨识结果进行对比。由表2可以看出，FSST重构的结果比较精确，而SWT由于出现了模态混叠现象，在高频域的振荡模态重构上出现了较大的偏差，主要因为模态混叠使得幅值及信号的包络线重构出现误差。模态能量混叠造成模态幅值的辨识误差；当衰减因子值较小时，对信号包络线极为敏感，使得IMT4出现了较大的误差。EMD方法的模态混叠严重失真使得和其他方法对比失去意义。对包含多个振荡模态的理想模拟SSO信号，FSST能将各个振荡模态进行分离并重构，辨识得到较为精确的信号参数，体现了FSST在含多模态的振荡信号分析中的优越性。

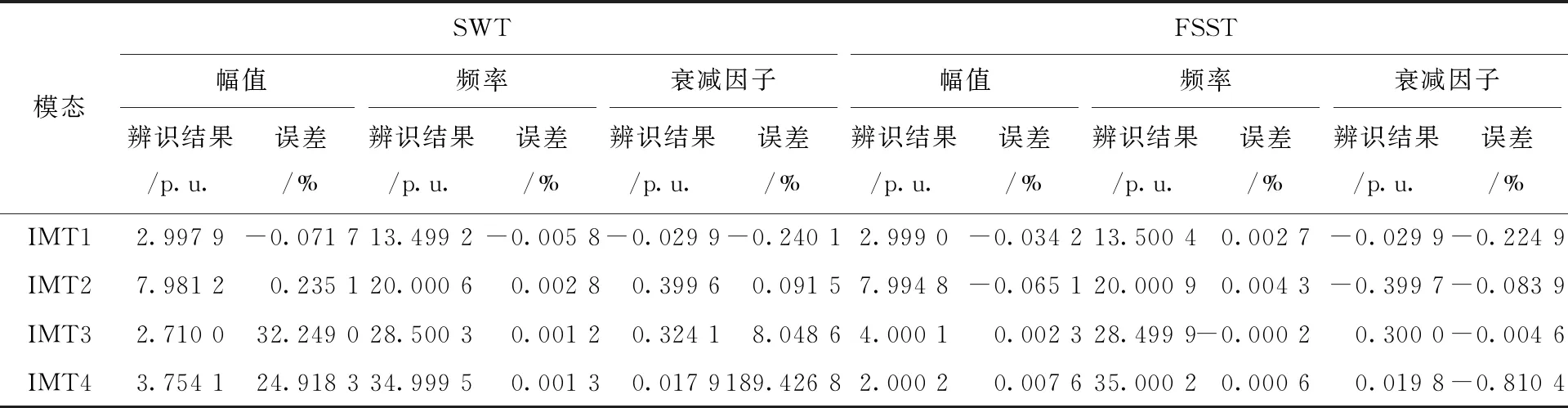
表2 仿真信号模态分量参数辨识结果

3.2 第一标准模型算例分析

在PSCAD/EMTDC中，建立次同步振荡IEEE第一标准模型时域仿真，如图10所示。发电机轴系部分的分解模型是将汽轮机轴系分为六个质量块模型。六个质量块分别对应：高压缸(HP)、中压缸(IP)、两个低压缸(LPA和LPB)、发电机(GEN)和励磁机(EX)，各质量块按顺序连在一个轴系上。该模型存在5个扭振频率，振荡频率分别为15.71、20.21、25.55、32.28、47.4Hz。

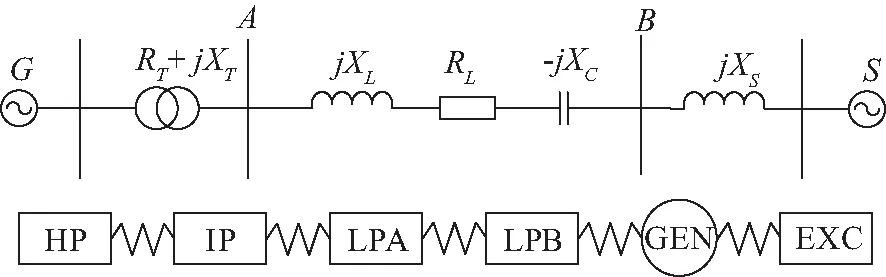
图10 IEEE次同步谐振第一标准模型

系统的基准功率取发电机的额定容量892.4 MVA，输电线路的额定电压为500 kV，频率为60 Hz。在系统节点B处三相短路接地故障以激发发电机组的振荡模态，故障起始时刻为1.5 s，仿真时间为5 s。选取机组的转速偏差信号作为分析信号，如图11(a)所示。对仿真信号进行FFT频谱分析，结果如图11(b)所示，可以看到该仿真信号包含5个振荡模态，其中存在着4个次同步振荡模态。

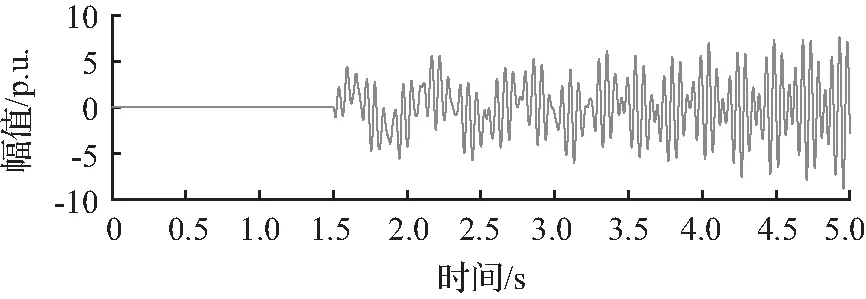
(a) IEEE第一标准模型转速偏差信号

信号的FSST总体时频分析得到的时频图如图12所示。由图12可知，该工况下的系统包含的4个次同步振荡模态中，处于15.5 Hz和20.2 Hz左右的两个振荡模态时频曲线较为明亮，能量呈现增长的趋势；而频率为25 Hz和32 Hz左右的振荡模态时频曲线颜色较为暗淡，能量较弱。说明在此工况下，处于15.5 Hz和20.2 Hz左右的两个振荡模态有发散的风险。

对图12采用D-K聚类提取时频图中包含的信息，聚类分析的情况如图13所示。

图12 转速偏差信号的FSST时频分析结果

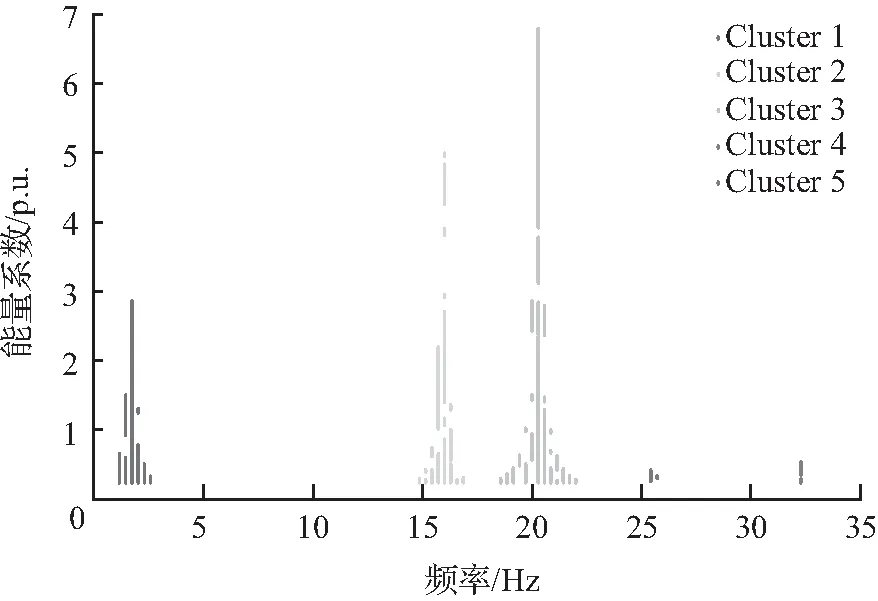
图13 D-K聚类提取的振荡模态中心频率

表3展示了聚类计算所得的振荡模态中心频率结果，可以看出，D-K聚类清晰地得到了4个同步挤压变量簇，即转速偏差信号内包含的4个振荡模态。振荡模态中心频率的计算结果精度较高，得到了准确的振荡模态频率。

表3 振荡模态中心频率提取结果

根据表3得到的振荡模态频率，重构各振荡模态，得到的各振荡模态重构结果如图14所示。可以看到，IMT1和IMT2的振荡模态幅值较大，即能量较强，而且呈发散趋势，其中IMT2的信号能量的增幅较为明显；IMT3和IMT4的振荡模态幅值较小，能量较弱。表明在此工况下，15.8 Hz和20.3 Hz左右的两个振荡模态为主导振荡模态，应注意频率为20.3 Hz左右的振荡模态有发散的风险。

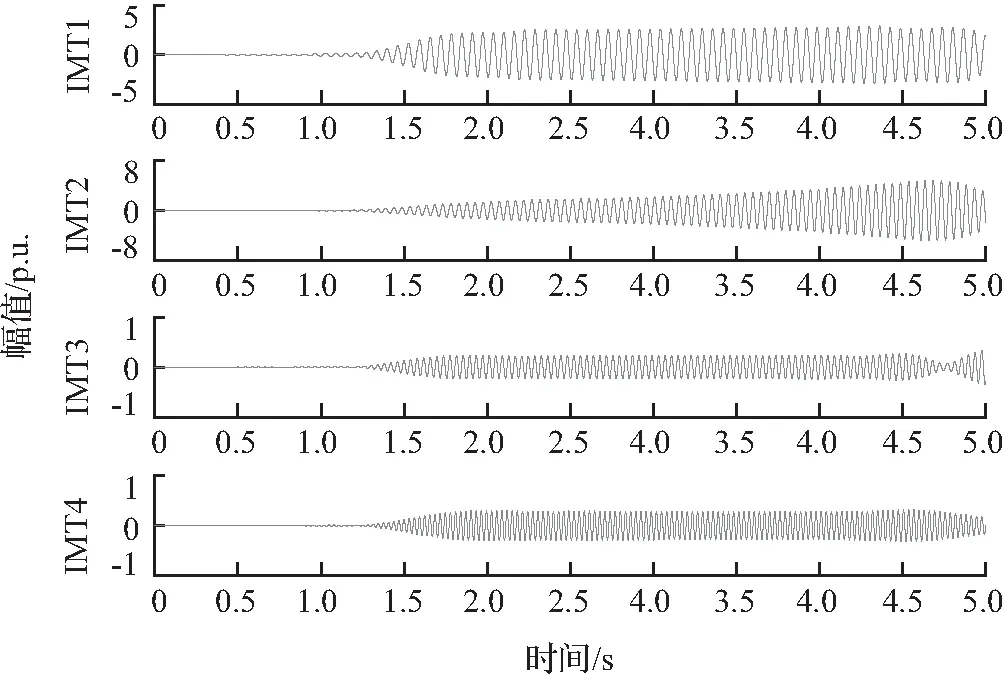
图14 重构结果

为得到更多关于振荡模态的信息，采用Hilbert变换对重构后的振荡模态进行信号参数辨识，获取振荡模态幅值、频率和衰减因子，仿真信号模态分量参数辨识结果见表4。为了证明FSST的抗噪性，增强白噪声使信号的信噪比达到10 dB。

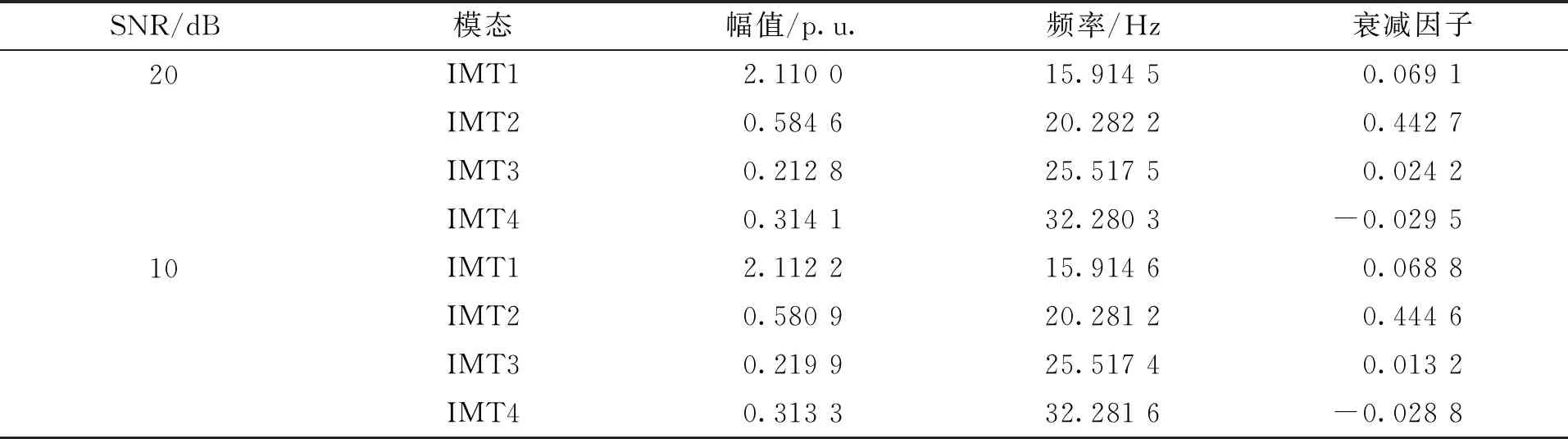
表4 仿真信号模态分量参数辨识结果

通过表4可以看出，信号内的IMT1-IMT3的衰减因子符号为正，说明为负阻尼模态，振荡会不断的发散，继而引发此单机无穷大系统的无法正常运行，需要采取抑制措施。同时当信噪比为10 dB时，辨识结果依旧准确，由此说明噪声对FSST的辨识精度影响不大，验证了FSST的抗噪性。

3.3 第二标准模型算例分析

前节所述的次同步振荡计算机仿真的第一标准模型发表于1977年。模型提供了一个可能产生振荡的简单模型，一个涡轮发电机连接到一个径向串联补偿传输线。该模型已广泛应用于研究方法的比较和研究不同类型的次同步振荡解决措施。但第一标准模型中采用的简单系统类型，其单串联谐振在电力系统的实际运行中很少遇到。因此，IEEE工作组于1985年在次同步振荡研究第二标准模型中提出了一种更常见的系统类型，该模型处理所谓的“并联谐振”以及具有共模的汽轮发电机之间的相互作用。

第二标准模型提供了两种系统配置作为基准模型。本文采用Simulink中提供的系统SYS-1配置，模型为一台连接到两条线路的发电机，其中一条是串联补偿的。模型中的发电机的额定容量为600 MVA，发电机有4个质量块模型，存在三个固有振荡频率分别为24.65、32.39、51.10 Hz。系统参数详见文献[29]，次同步振荡第二标准模型SYS-1如图15所示。

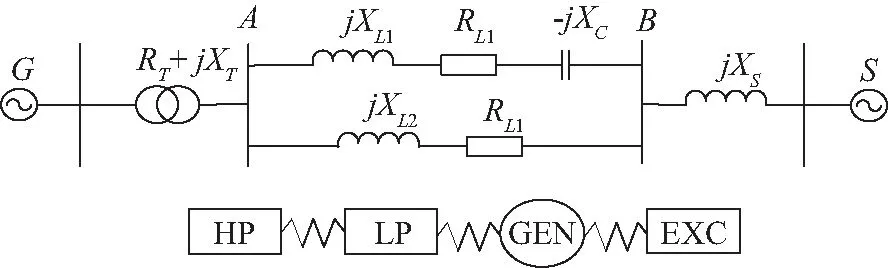
图15 IEEE次同步谐振第二标准模型SYS-1

经Simulink仿真后获得时域信号作为研究对象，研究系统的振荡问题。本文选取系统中发电机的GEN-LP之间扭矩作为待分析信号，仿真时间为5 s，采样频率为1 kHz，信号的信噪比为20 dB，信号和FFT频谱分析结果如图16所示。

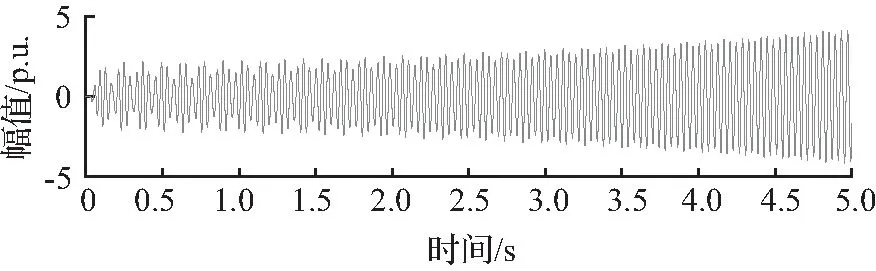
(a) IEEE第二标准模型GEN-LP扭矩信号

扭矩信号经FSST分析得到的总体时频分析结果如图17所示。在25 Hz下方产生了1条清晰的时频曲线，说明系统发生了次同步振荡。曲线的色彩随着时间不断变亮，表明此频率下的振荡模态能量不断增加，模态不断地发散。

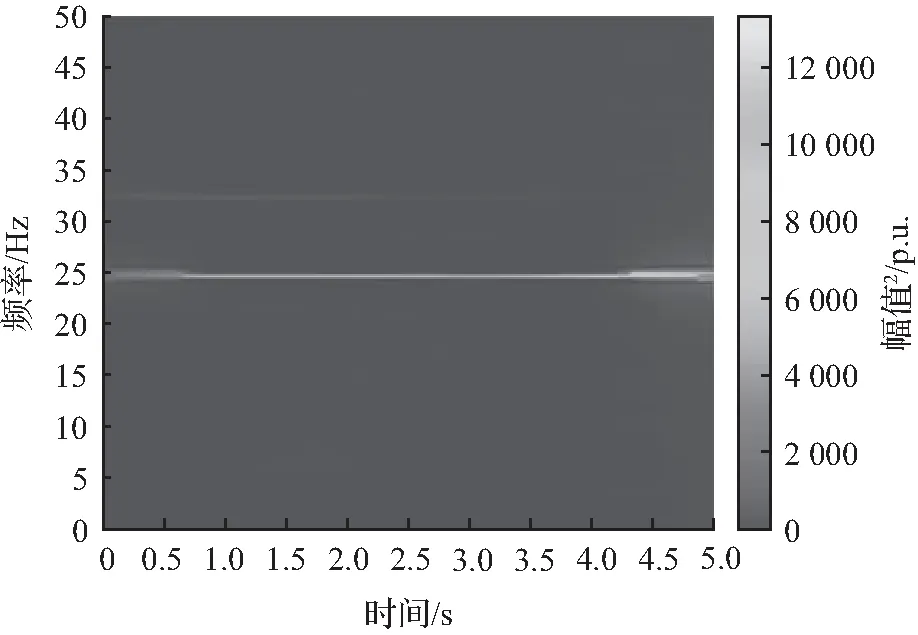
图17 IEEE次同步谐振第二标准模型GEN-LP扭矩信号的FSST分析结果

因此，使用D-K混合聚类分析将总体时频分析得到的时频结果提取出来，确定振荡模态的振荡频率。聚类的结果如图18所示，计算得到的振荡模态中心频率提取结果见表5。

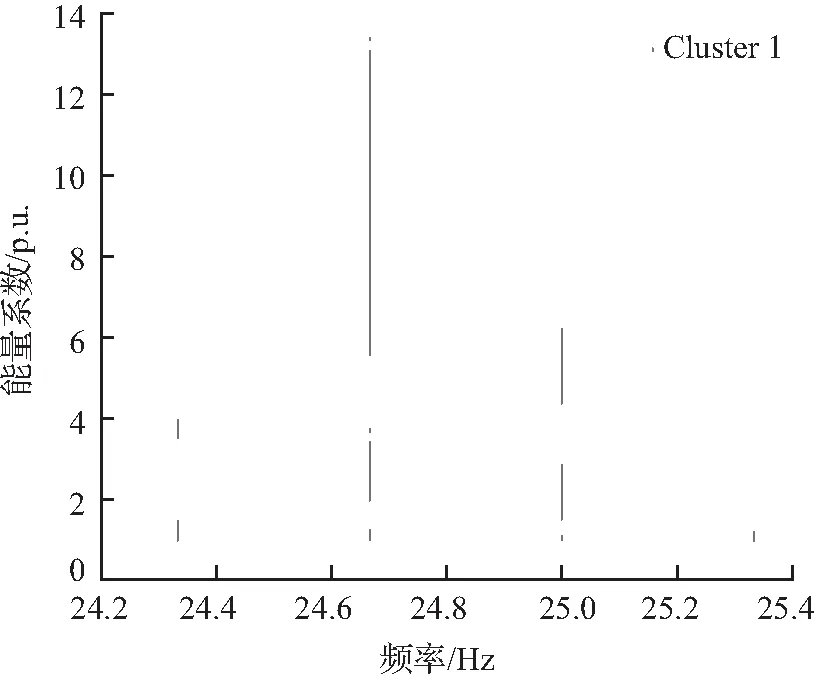
图18 D-K聚类提取的振荡模态中心频率

表5 振荡模态中心频率提取结果

由表5可以看出，D-K混合聚类分析只识别出来一种振荡模态的振荡频率，另一种振荡模态的能量太小低于阈值被过滤无法形成类簇。聚类获得了精度较高的已识别模态振荡频率，证明所提聚类算法的有效性，同时从侧面验证FSST的“挤压”效果。因验证模态能量过于微弱，且为自行收敛模态，根据总体时频分析结果，选择对应频率区域重构这一模态。振荡模态的重构结果如图19所示。

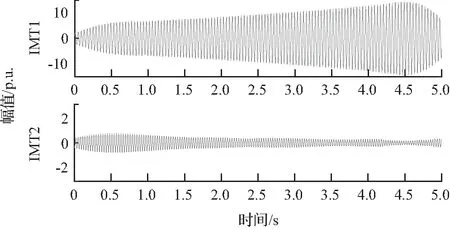
图19 振荡模态的重构结果

表6展示了混合聚类后提取的振荡模态中心频率，结合图19可以看出，IMT2的幅值相对IMT1小太多，能量较弱且衰减因子为负，可自行收敛，无需过多关注。经FSST分析重构，参数识别后得到的模态振荡频率精确度较高。IMT1幅值较大，衰减因子为正，表明此振荡模态将会不断增大发散，第二标准模型SYS-1系统发生了次同步振荡现象。根据系统参数及分析所得频率结果，可判断振荡模态为频率为24.65 Hz的固有模态。

表6 D-K聚类提取的振荡模态中心频率

4 结语

本文提出一种采用D-K聚类分析与FSST结合的电力系统次同步振荡信号时频分析方法。结合DBSCAN可以分类集群类本身的特点与Kmeans可以计算集群类中心的特点，它解决了FSST需要通过观察法才能获取振荡模态数量的问题和FSST选择信号重构区间不足的问题，增加了FSST方法的方便和实用性。同时将FSST引入次同步振荡信号辨识，解决了SWT方法对小波基选取存在依赖使得难以用于模态辨识的问题。FSST拥有更强的抗模态混叠能力，提高了对振荡模态的时频分辨率。可更好地服务于次同步振荡信号的模态提取分析，得到较高精度的模态参数，有利于对电力系统次同步振荡现象的分析以及抑制措施的研究。