基于密度泛函理论的团簇Co3MoS催化性质研究

2021-11-08王智瑶方志刚曾鑫渔毛智龙吴庭慧朱依文

天然气化工—C1化学与化工 2021年5期

王智瑶，方志刚，曾鑫渔，毛智龙，秦渝，宋嘉，吴庭慧，朱依文

（辽宁科技大学化学工程学院，辽宁鞍山 114051）

近年来，由于经济快速发展，大量化石燃料被粗放消耗，环境和资源问题日益突出，清洁能源的开发已成为当今科学研究热点[1-3]。清洁能源的高效获取离不开性质优异、活性良好的催化剂，目前所研发的催化剂中满足该条件的基本为贵金属催化剂。但由于贵金属催化剂成本高且不易获取[4]，因此价格便宜且物理化学性质表现相对较好的非晶态合金类催化剂被各行业广泛应用[5,6]。Co-Mo-S体系便是近年来应用较多的一类催化剂。 Ren等[7]通过在(NH4)2MoS4溶液中对碳纤维上的纳米片阵列进行水热处理，得到了高性能无定形的Co-Mo-S纳米片阵列，当其参与析氢反应时，其制作的纳米片阵列表现出了显著的活性。 Mukundan等[8]制备了在活性炭上负载具有促进作用Co的Mo-S纳米催化剂，可用于在液相中对木质素衍生的酚进行选择性加氢脱氧，在实践过程中该催化剂表现出了出色的催化活性。研究表明，Co-Mo-S在光反应下也表现出了较高的催化活性[9]。同时，在加氢脱硫反应中Co-Mo-S也表现出了较好的性能[10,11]。纳米级的Co-Mo-S材料被认为是用于构建C-S键结构的出色催化剂[12]，该反应是通过氢自动转移（借入氢）机制发生的。对于析氢和析氧反应而言，制造低成本、原料丰富且稳定可靠的双功能催化剂是很有必要的， Lu等[13]用一种基于多金属氧酸盐的分子方法构建了纳米片Co-Mo-S催化剂，从其实验中发现Co-Mo-S具有出色的析氢、析氧和整体水分解催化性能。对于可持续发展的能源系统而言，制作用于电化学析氢反应（HER）和尿素氧化反应（UOR）的高效、低成本和高稳定性的催化剂非常重要，Li等[14]在碳布（CC）上合成了分层的Co-Mo-S纳米片，所制备的纳米片材料具有丰富的活性位点并在一定条件下对电化学HER和UOR表现出了优异的催化性能。

密度泛函理论[15]是量子化学中重要理论之一，该理论主要是以电子密度替代波函数作为基本研究单元，用电子密度来表述和判断体系的性质。近年来，密度泛函理论在微观粒子的电子结构研究中大量使用[16,17]，对于含有过渡金属原子或离子的体系更显现出优越性。密度泛函理论已被成功地应用于物质结构和性质、磁性产生、化学催化反应机理、过渡态结构和活化势垒等问题的研究。团簇是通过一定的作用力组成的相对稳定的微观聚集体，它是连接宏观与微观之间物质构造的新层次。团簇模型[18]广泛存在于生产实际和理论研究的活动中，该模型的主要特点在于采用局域化的原子集团模型用以模拟整个晶体，该模型方法是研究非晶态材料局部性质的有效方法。团簇模型的不断发展，引起了化学、材料、凝聚态物理等多个学科的共同关注，并且随着理论和技术的深层次发展，对团簇模型的结构和性质从密度泛函理论出发进行热力学和动力学等理论分析成为了可能，这极大地加深了对一种物质的研究深度并拓宽了研究空间。

不难看出，Co-Mo-S体系在催化剂方面有着较多的应用，但普遍缺乏在微观领域探究其催化性能是如何产生的研究，为了理清Co-Mo-S体系催化作用机理以及活性位点的位置和影响，同时也为了给其他科研人员在设计催化剂时提供一定价值的理论参考，本文依据文献[14]和团簇模型理论设计出团簇Co3MoS用来模拟Co-Mo-S体系，并以密度泛函理论为基础，从该团簇模型的HOMO和LUMO轨道贡献率、能隙差、态密度图、HOMO和LUMO图及库普曼斯定理等方面，开展得、失电子能力及反应活性等相关理论的研究。

1 模型和计算方法

选取合适的团簇模型尤为关键，其既能反映非晶态材料的局部结构，又不失小范围内的晶体对称性，从而可对局部的电子结构、物理和化学性质进行理论探讨和预测。 B3LYP杂化泛函是量子化学计算领域中应用最广泛、综合性能最强的经典泛函，可以对过渡金属元素和开壳层结构进行较为准确的计算，而Lanl2dz赝势基组是目前广为使用的有效核势（ECP）基组之一，运算过程较为可靠和稳定。根据拓扑学原理及密度泛函理论，在Gaussian09[19]量子化学软件辅助下，运用B3LYP泛函和Lanl2dz基组，分别在二、四重态下对团簇Co3MoS设计的20种初始构型进行了结构优化，经过频率验证和排除相同构型后，最终在二、四重态下分别得到四种稳定构型。其中对Co、Mo和S原子采用Hay[20]从头算计算基组，即18-eECP双ξ基组（3s，3p，3d/2s，2p，2d），S原子加极化函数为ξS,d= 0.55[21]。以上所有运行和计算均在计算机HP-Z440上完成。

2 结果和讨论

2.1 团簇Co3MoS稳定构型

设计团簇Co3MoS的初始构型主要有平面五边形、三角双锥型及四棱锥型三种初始形态。排除经Gaussian09分析后的相同构型和含虚频构型后，最终得到8种稳定构型。通过对稳定构型的能量比较得知，四棱锥构型1(4)较其它构型而言最为稳定，三角双锥构型4(2)稳定性最差。以构型1(4)能量为参考，并将其能量设为0 kJ/mol，其它构型能量以此为基准重新计算，并按能量从低到高原则对8种稳定构型排序，如图1所示（括号内数字表示重态）。

图1 团簇Co3MoS优化构型及能量Fig. 1 Optimized configurations and energy of cluster Co3MoS

由图1可知，经排除剩余后的稳定构型主要以四棱锥型、三角双锥型和单帽三角锥型3种空间形态存在，说明立体构型比平面构形较为稳定。其中三角双锥构型比其余两种构型形态稳定存在得较多，有1(2)、2(4)、3(4)、4(4)、4(2)等5种构型；四棱锥构型有1(4)和3(2)；单帽三角锥构型有2(2)。

2.2 团簇Co3MoS各原子HOMO、LUMO轨道贡献率

上世纪50年代，福井谦一[22]提出了前线电子的概念，之后以此概念为雏形，又进一步提出了对研究化学反应等问题有着重要支撑的前线轨道理论。由前线轨道理论可知，HOMO轨道（能量最高占据轨道）和LUMO轨道（能量最低未占轨道）对催化反应活性有着关键性作用[23]。因此，为了找出团簇Co3MoS潜在的活性位点，根据前线轨道理论计算出了团簇Co3MoS中Co、Mo、S原子分别对HOMO和LUMO轨道的贡献率，具体数据如表1所示。

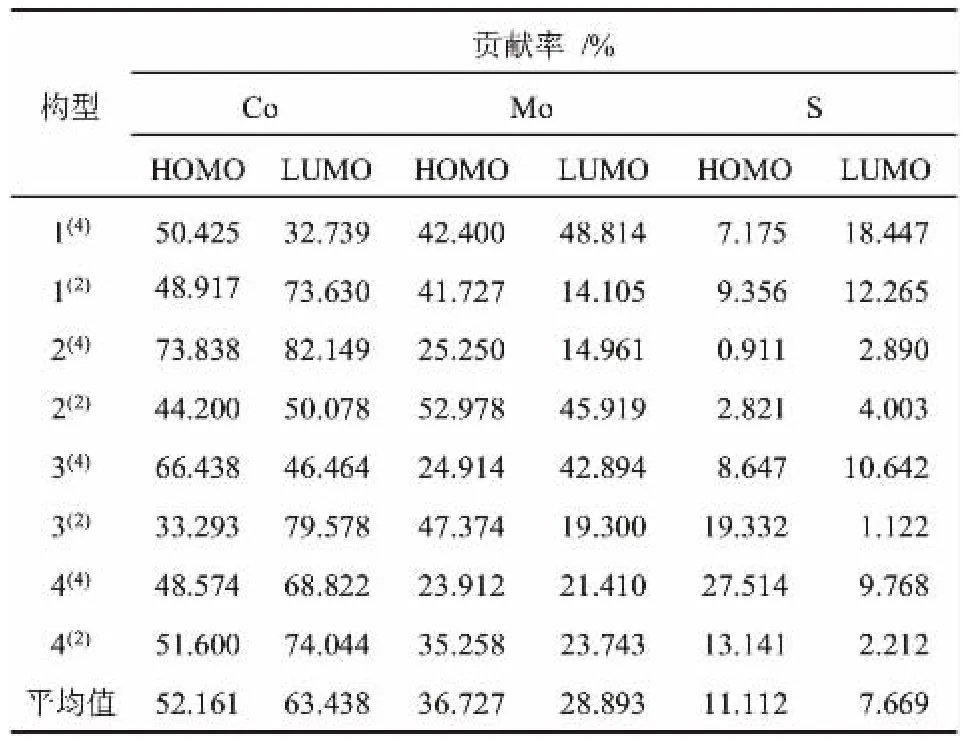
表1 团簇Co3MoS各原子对前线轨道贡献率Table 1 Contribution rate of each atom of cluster Co3MoS to frontline orbitals

从表1中可知，团簇Co3MoS中Co、Mo、S三个原子对HOMO和LUMO轨道的贡献率均大于0，说明三个原子对团簇Co3MoS的活性都有一定的贡献，其中构型2(4)的S原子对HOMO轨道的贡献率（0.911%）为全局最小。不难看出，除构型4(4)中S原子对HOMO轨道贡献率（27.514%）较大外，其余构型中的金属原子Co和Mo对HOMO和LUMO轨道的贡献率普遍比本构型中的非金属原子S对轨道的贡献率要大，这可进一步推测出团簇Co3MoS金属原子的活性比非金属原子大[24]。对金属原子Co和Mo的HOMO、LUMO轨道贡献率分析可知，除构型2(2)、3(2)中Co原子对HOMO轨道贡献率（44.200%、33.293%）比其对应的Mo原子小（52.978%、47.374%）、构型1(4)中Co原子对LUMO轨道贡献率（32.739%）比Mo原子小（48.814%）外，其余构型中的Co原子对HOMO和LUMO轨道贡献率均比Mo原子大，说明团簇Co3MoS中Co原子提供的活性相对Mo原子较多，是该团簇的潜在活性位点[13]。结合团簇Co3MoS中各原子对HOMO、LUMO轨道贡献率平均值来看，Co原子对两类轨道的平均贡献率（52.161%、63.438%）远大于 Mo 原子（36.727% 、28.893%）和S 原子（11.112%、7.669%）的贡献率，这正好印证了前面得出的“Co原子是潜在活性位点”的结论。

2.3 团簇Co3MoS活性能隙差、费米能级、态密度图分析

物质的催化活性大小可以由能隙差（EGAP）来表征[25,26]，能隙差计算方法为LUMO能级与HOMO能级之间的差值（EGAP= ELUMO- EHOMO）。一个物质的能隙差越小，表明该物质的活性能力就越强；能隙差越大，则该物质的活性能力越弱。费米能级由HOMO能级与LUMO能级相加和的一半得出（EFermi= (ELUMO+EHOMO) / 2），通过计算，团簇Co3MoS 8种稳定构型的能隙差数据如表2所示。

表2 团簇Co3MoS的前线轨道能级、费米能级和能隙差Table 2 Frontline orbital energy level, Fermi energy level and energy gap difference of cluster Co3MoS

由表2可知，构型3(2)能隙差最小（139.266 kJ/mol），说明该构型相比其它构型具有更强的催化活性能力。结合轨道贡献率来看，构型3(2)中的潜在活性位点Co原子对LUMO轨道贡率也较大，其值为79.578%；能隙差最大构型为1(4)（189.868 kJ/mol），表明其活性能力在所有稳定构型中最差。

电子云密度一般由态密度图来分析，通过Multiwfn程序得到该团簇各构型的态密度如图2所示。图中虚线表示费米能级，费米能级是表征物质催化活性能力的又一种方法[27-29]。费米能级附近的电子云密度大小可反映出该物质的催化活性能力高低，电子云密度大，则该物质的催化活性能力便较强。费米能级左侧表示物质在化学变化中提供电子的能力，费米能级右侧表示物质在化学变化中接受电子的能力。提供和接受电子能力在催化反应中都可反映出该物质的催化活性的强弱，并且可以根据费米能级左右两侧的最高峰分别距其的距离来判断物质的得、失电子能力大小，距离费米能级越近其得、失电子能力就越强。

图2 团簇Co3MoS的态密度Fig. 2 Density of states of cluster Co3MoS

由图2可知，团簇Co3MoS 8个稳定构型中，费米能级距左侧最高峰的距离均小于距右侧最高峰的距离，表明该团簇的8种稳定构型在催化反应中都具有较强的提供电子能力。其中4(4)、4(2)两构型左侧最高峰距离小于右侧更加明显，说明这两个构型比其它构型的提供电子能力更强；不难看出，构型2(4)、2(2)相比其它稳定构型而言左侧最高峰距费米能级距离稍大些，因此其提供电子能力可能比其它构型稍弱些，但也不能忽略。从图中进一步发现，费米能级左侧只有一个峰，而费米能级右侧却有多个峰，且右侧峰面积明显大于左侧峰，此外构型2(4)和4(2)最高峰均在费米能级右侧，其余构型的费米能级右侧最高峰相较于左侧最高峰高度也较为接近，进一步说明费米能级右侧的峰对催化活性也有一定的影响，同时也表明团簇Co3MoS的接受电子能力也较强。由Co、Mo、S三个原子对前线轨道贡献率可知，Co原子相比Mo和S原子而言对HOMO轨道、LUMO轨道的贡献率最大，分别为52.161%、63.438%，可推测出Co原子是造成费米能级两侧最高峰的主要影响因素。Mo原子、S原子对HOMO轨道的贡献率（36.727%、11.112%）均大于其对相应的LUMO轨道的贡献（28.893%、7.669%），这便是在态密度图中费米能级右侧除最高峰外其余峰产生的主要原因。

整体来看，团簇Co3MoS具有一定强度的得、失电子能力，进一步说明其催化活性能力也较强[14,30]，这正好印证了前文中Co-Mo-S在实际应用下具有较高的活性这一观点。同时，费米能级两侧的最高峰也为Co-Mo-S成为双功能催化剂提供了潜力。

2.4 团簇Co3MoS活性HOMO、LUMO图分析

前线轨道的HOMO、LUMO图是判断物质得、失电子能力进而判断化学反应活性的又一方法。团簇Co3MoS各稳定构型的HOMO图和LUMO图如图3所示。图中各原子周围的不规则区域为电子在此部分出现的概率，电子出现时所形成的覆盖面积则代表前线轨道中的离域空间，其与物质的活性密切相关。图中白色表示轨道波函数的正相位，黑色表示轨道波函数的负相位。图3中HOMO图面积大小表示其对应构型的提供电子能力的强弱；LUMO图面积大小代表得到电子的能力。整体来看，团簇Co3MoS各构型内的HOMO图和LUMO图面积大小差距不是太大，并未形成明显的差异，因此可以说明团簇Co3MoS的得、失电子能力都具有一定的强度，其活性能力也较强，这点与分析态密度得出的结论相一致。

图3 团簇Co3MoS各构型HOMO和LUMO图Fig. 3 HOMO and LUMO diagram of each configuration of cluster Co3MoS

从图3中进一步发现，构型2(2)、3(2)、3(4)、4(4)、4(2)的HOMO和LUMO图面积相比其它构型而言较大，各原子形成的轨道波函数正负相位重叠部分较多，说明以上5种构型的得、失电子能力比其它构型更强，进一步也表明其活性能力也稍强。反观构型1(4)和2(4)其HOMO和LUMO图面积比其它构型较小，尤其是构型2(4)的HOMO和LUMO图中的Co1和Co2原子外围电子出现概率的面积，表明以上两个构型在该团簇稳定构型中得、失电子能力比其它构型弱，其催化活性能力也随之较低。通过对不同重态构型的HOMO和LUMO图面积大小对比分析得出，重态对得、失电子能力的影响并没有必然的联系。

2.5 团簇Co3MoS活性库普曼斯定理分析

电离势（EI）、电子亲和能（Eea）、电负性（）和亲电指数（ω）4种物理量是衡量物质活性又一判断方法。电离势值越大，其对应物质的反应活性就越差；电子亲和能则恰恰相反，其值越大，对应物质的反应活性就越强；电负性和亲电指数分别代表了物质在催化反应中吸引和接受电子的能力，两种量的数值越大，其活性就越强，对其反应就越能起到促进作用。由库普曼斯定理可知，以上4种物理量分别由式(1)～式(4)计算得出：

式中，EI为电离势，kJ/mol；EHOMO为HOMO轨道能级值，kJ/mol；Eea为电子亲和能，kJ/mol；ELUMO为LUMO轨道能级值，kJ/mol；为电负性，kJ/mol；ω为亲电指数，kJ/mol。

采用库普曼斯定理计算所得结果如表3所示。

表3 团簇Co3MoS反应活性参数Table 3 Reactivity parameters of cluster Co3MoS

由表3可知，该团簇的亲电指数波动较其余物理量更为剧烈，其极大极小两个值相差为486.642 kJ/mol，远远高出了电离势、电子亲和能和电负性的极值差（73.685 kJ/mol、78.014 kJ/mol和70.275 kJ/mol）。其中构型3(2)的亲电指数最大，为1148.570 kJ/mol；同时，构型3(2)的电子亲和能、电负性数值也最高（330.313 kJ/mol、399.946 kJ/mol）。由此推测，构型3(2)有着较强的得、失电子能力，相比其它构型有着较强的催化活性，与上文能隙差分析所得结论一致。