基于蚁群算法的受电弓故障检修管理优化

顾建凯

（南京铁道职业技术学院 机车车辆学院，讲师，江苏 南京，210000）

1 引言

本文研究如何提高受电弓故障检修维护管理效率。对工业应用设备故障检修维护管理程序优化分析，学术研究中主要有两种方式：一种是结合设备结构和应用原理，并通过对预期故障建模或将现场典型故障汇总建模从而对设备后期运行维护形成管理风控的理论支持；另一种是通过长时间检修故障信息累积进行模型数据嵌入和相关结论分析。本文旨在兼顾两种方式进而得以户型验证从而达到结论的准确性。

本文以TSG15B型受电弓结构和工作原理为分析基础，结合机车应用过中受电弓故障情况以及检修人员相关工作，从两个方向对故障信息进行权重指标分析。一方面基于故障树和各故障点影响度；另一方面通过基于蚁群算法的模糊层次分析法明确各故障底事件的权重指标，完成对受电弓故障理论分析，并将两方面数据互相比较以增强结论鲁棒性，达到提高处置故障效率进而降低故障发生概率研究预期。

2 受电弓失效分析及故障树建模

2.1 TSG15B受电弓功能失效分析

以电控气动为动作机理的受电弓在弓网耦合机制下高速运行并从接触网上汲取电能，其故障形成原因主要有两方面：一是自身机构原因，如机械零部件、升降弓气路和逻辑控制阀板等故障导致受电弓无法正常工作；二是外部环境因素，如雨雪天工作环境恶化、突发物件撞击等造成受电弓功能实效。受电弓典型故障见表1。

表1 受电弓典型故障

2.2 TSG15B受电弓故障树建模鉴于TSG15B型气囊式受电弓组成零部件繁多、电控气动机理关联较为复杂以及与机车其他电器设备存在硬件连接和逻辑联系，实际应用要综合考虑受电弓应用故障的多源异构特点，通过故障树对受电弓故障关联建模，能够明了表示出器件各组成部件以及各故障状态联系，为后续进一步数学分析提供依据［1］。受电弓故障树的建立分成三层结构，以表格中“T受电弓故障”作为顶事件，“A1-A5”作为中间事件，“X1-X24”作为底事件，其中逻辑关系为A1-A5之间为或的关系都可引发顶事件的发生，底事件中除了X23和X24需要共同发生才会引起A5中间事件的发生，其他底事件都为或的关系，其发生都会引起对应中间事件的发生。

2.3 受电弓故障树定性和定量分析通过定性和定量对模型进行初步分析，其中定性分析的目的在于明确底事件当中的最小割集，最小割集的集合映射出了受电弓失效的全部故障种类，也即明确了故障树当中的系统薄弱环节。在分析过程中采用下行法，即自上而下对故障树进行探究，以下层事件替换上层事件，如事件为与的关系则将其添加入对应割集中去，如为或的关系则增加割集数量即可，如此重复直至所有事件都替换为底事件，再通过布尔函数进行简化至确保统一割集中事件关系都为相与即可得到最小割集［2］。根据以上要求可以明确出受电弓故障树模型的布尔表达式（见式1），在明确好最小割集的基础上。

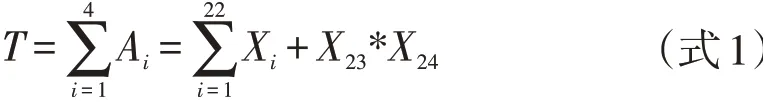
定量分析基于定性分析的结果对目标顶事件（受电弓失效）发生的概率进行估算，以TSG15B型受电弓百万公里故障率为采样参数，对各底事件概率进行统计。共对样本中的6台机车进行数据采集，日行5 506 km，年度走行为3 920 450 km。通过故障树定性分析可以得知故障底事件的逻辑关系，再结合概率公式（式2）进行顶事件受电弓故障概率计算，最终可以得到受电弓故障顶事件发生概率可以用公式（式3）表示。

将表格中各底事件发生概率代入公式当中可得受电弓故障发生的概率为0.197，以百万公里的故障率来看还是比较高的，原因在于其中计入了接触压力匹配度差的这一考虑因数，而从应用角度讲，目前的弓网接触压力都是事先设定好的固定参数，所以很难根据现场使用环境进行自动对应调整，该处寄望于后期在受电弓主动控制环节进行进一步的智能控制实现。

2.4 故障底事件的重要度分析故障树底事件的重要度分析包括结构重要度、概率重要度以及关键重要度，本文以反映各基本底事件概率变化对受电弓故障概率影响的关键重要度进行数值统计分析，各底事件的关键重要度根据式4进行计算，其中g（P）为顶事件的发生概率，g（1iP）为对应底事件发生时顶事件发生的概率。

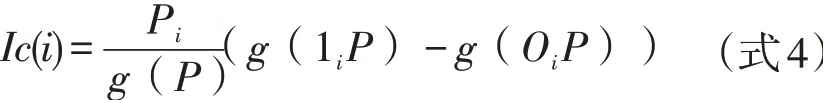
运用公式及前述受电弓故障发生的概率和各底事件故障率进行关键重要度数据统计，通过故障树中定量分析中的底事件重要程度对比分析其中碳滑板因为接触压力匹配度差、弓网之间滑动摩擦引起的物理损耗、雨雪天因为较易引起弓网之间的拉弧进而引起碳滑板灼伤，与现场应用中所反映出的故障情况相符，但该分析体系有赖长时间故障事件积累，相关部件的周期性使用劳损将会出现，导致故障概率进一步增大。鉴于该分析结果有一定的片面性，本文采用模糊层次分析法对故障底事件重要度进行计算。

3 模糊层次分析法矩阵

模糊层次分析法具备良好的数学表达能力，可以将其与故障树分析法进行有效结合从而方便求取各底事件相对顶事件的重要度数值［3］。模糊层次分析法步骤如下：①目标明确；②搭建层次模型；③根据专家评测明确同一层各因数相对重要度；④搭建模糊判断矩阵；⑤计算各因数重要度数值。在分析过程中前2步的建模过程与故障树分析法是一致的，之后对同一层各事件元素之间相对重要度依据专家参与制定的受电弓故障0.1-0.9九标度法进行模糊判断矩阵建模。

由于受电弓各故障间关联性强弱不尽相同、依据九标度法所构成的判断矩阵往往很难具备一致性，解决的方法是首先通过以上九标度法的度量标准衡量比较，并且满足于aij+aji=1（i，j=1，2，...，n）［4］，即可得到底事件X1-X22，X23*X24相对于顶事件受电弓故障的模糊判断互补矩阵，矩阵形式如下所示，再经由一定的变换使得矩阵具备一致性，也即满足等式aij=aik-aik+0.5，其中一致性具备当中的每个元素表示为：也即将原模糊判断矩阵按照行进行求和）。

4 权重优化分析

在通过现场专家经验并且结合模糊层次分析法当中的数学转换计算即可得到反映受电弓故障底事件两两之间重要程度关系的模糊一致判断矩阵，而模糊一致判断矩阵所反馈的关系信息决定了是可以基于其本身的数值关系来求取每个元素的权重指标。设每个底事件X1-Xn对应的权重值为w1-wn，根据文献［5］所述内容，有关系式rij=0.5+a（Wi-Wj）（i，j=1...n）成立，最终权重值求解将以

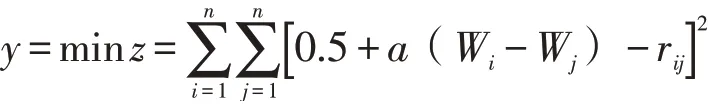
考虑计算数据量繁多，本文采用蚁群算法，此法模拟了同等时间内蚂蚁觅食以外激素浓度作为信息传递媒介并因此形成信息正反馈，其算法思想吻合于模糊判断矩阵进行权重值最优值的求解，设定运行参数为：蚁群规模为50，最大迭代次数为100，信息重要度因子、启发函数重要程度因子、信息素挥发因子、常系数分别为1、6、0.2、8，通过迭代求解，每次运算完成对信息素进行更新，并且记录当次运行的最优解，通过MATLAB进行软件算法迭代100次后，得出最优权重适应度变化图形如图1所示，从图中可以观察到大约40次迭代后达到收敛状态，最终得到的蚁群觅食终点即为每个故障底事件的重要度数值为［0.04368 0.02918 0.13568 0.02256 0.02286 0.02255 0.04915 0.02816 0.05129 0.04512 0.0015 0.04745 0.04815 0.04622 0.04815 0.02025 0.02011 0.04335 0.4015 0.1991 0.04991 0.02451 0.05119 0.1991］。

图1 底事件重要度计算收敛度

通过故障树定量分析中的底事件重要度数值确认对比基于蚁群算法的模糊层次分析法的底事件重要度计算数值结果，通过图2可以发现对应重点底事件的重要度数值接近，同时也满足现场受电弓检修实际，该理论分析结果能够对现场受电弓的检修起到支持和帮助作用。

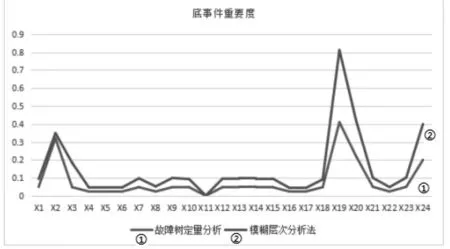
图2 受电弓故障底事件重要度数值

5 结论

综上所述，通过对受电弓故障点分别进行以现场检修数据为建模基础的故障树分析，以及基于蚁群算法的模糊层次法分析，两者结论趋于一致，可以得出受电弓故障中，以碳滑板结块，裂纹的重要度权值最高，滑板气管破裂故障紧随其后，所以在检修维护中要关注与接触网进行高速相关摩擦接触的碳滑板部分；控制环节部分在检修维护过程中要加强单部件检修完成后重新组装的气密性试验以保证运行的可靠性。