超声铣削对镁合金在模拟体液中腐蚀性能的影响

李甜，马保吉，边建潇，屈锋，程杰

（西安工业大学 机电工程学院 陕西省特种加工重点实验室，西安 710021）

我国人口老龄化问题日益严重，骨损伤患病率逐年增长。镁合金因密度低、相对比强度高且具有优良的可降解吸收性和生物相容性，成为一种新型可降解植入材料，被广泛应用到医疗领域[1]。但其耐蚀性较差，用作骨植入材料必然要进行机械加工，这会影响材料表面的完整性。牛金涛等人[2]研究表明，材料的腐蚀性能与其表面完整性密切相关。因此，探究一种合适的表面改性机加工工艺方法来提高镁合金的耐蚀性，对医用镁合金的应用推广有着举足轻重的意义[3]。

镁合金的切削性能良好，一般采用最广泛的机加工方式（铣削）进行加工，但在铣削过程中，伴随着切削力以及切削热的产生，这对材料表面质量影响较为明显，故超声振动切削技术应运而生。超声振动切削的加工原理是：在切削加工中引入超声波信号，刀具频率为20～50 kHz，沿切削方向高速振动，将连续的加工方式改变为周期性分离的脉冲式加工[4]，进而降低切削力以及切削热。因此，基于传统铣削工艺，通过施加超声振幅，可改善铣削系统的动力学特性，降低铣削力和铣削温度，最终实现改善材料表面完整性的目的[5]。

评价材料表面完整性的重要指标有表面粗糙度和表面硬度等[6]，二者的变化会对材料表面加工质量造成较大影响[7]。近年来，不少国内外学者探索了超声铣削工艺的加工参数对表面完整性的研究，并取得了丰硕的成果。Pradeepkumar 等[8]利用响应曲面法（RSM）探究了铣削工艺参数对AZ91D 镁合金表面粗糙度的影响，并对响应目标进行优化。Reza Teimouri 等[9]基于RSM 研究了超声辅助抛光工艺参数对6061-T6 铝合金表面粗糙度和硬度的影响，在给定范围内，得到了粗糙度最小、硬度最大的最佳工艺参数。Yixuan FENG 等[10]在不同工艺参数下进行了传统铣削和超声铣削铝合金的对比实验，得到表面粗糙度的变化规律。Roy 等[11]通过普通铣削与超声铣削钛合金的对比试验，验证了超声铣削加工钛合金的优势。牛金涛[12]研究了铣削工艺对2A97 合金表面完整性及腐蚀行为的影响，发现表面粗糙度的增大会导致材料耐腐蚀性能降低，而引入加工硬化后，材料的耐腐蚀性能得到增强。以上文献的结果表明，可以通过超声铣削工艺对材料进行表面改性，以提高材料的耐腐蚀性能，但鲜有文献报道超声铣削工艺对镁合金腐蚀特性的研究。

因此，本文将AZ31B 作为研究对象，基于RSM采用中心复合试验方法（CCD）建立了回归预测模型，探析超声振动铣削加工参数对材料表面完整性以及腐蚀性能的影响规律，根据电化学试验结果，探讨了表面完整性与腐蚀性能间的关系，最终确定了超声铣削工艺的最优参数条件，为镁合金作为一种新型医用材料的应用推广提供理论支撑。

1 试验

1.1 平台

超声铣削试验材料为AZ31B 型号的镁合金锻压板（诚硕金属材料有限公司，河北）。表1 为AZ31B的化学组分。表2 为AZ31B 的机械性能参数。铣削设备为VMC850 立式加工装置（鲁南有限责任公司，山东），其最高工作转速为8000 r/min，如图1a 所示。刀具为硬质合金（YG10X）四刃立铣刀（HE4A08060-8.0），直径为8 mm，铣削方式采用顺铣。超声振动设备为HKUSM35-20 型的豪克能加工系统（华云机电科技有限公司，山东），其振动频率为40 kHz，振动方式为轴向振动铣削（即工件的振动方向垂直于加工表面），如图1b 所示。表面粗糙度（Ra）采用白光干涉轮仪（Talysurf CCI）进行测量，其分辨率为8 nm，测量结果用已加工面上随机3 点位置的Ra均值代替。硬度采用电子布氏硬度计（THB-3000E）进行测量，压头钢球直径为5 mm，压力为2452 N，负荷保持时间为30 s，取已加工面上3 处随机位置的压痕直径均值作为表面硬度（HB）。

表1 AZ31B 的化学组分Tab.1 Chemical components of AZ31B wt.%

表2 AZ31B 的机械性能参数Tab.2 Mechanical properties f AZ31B

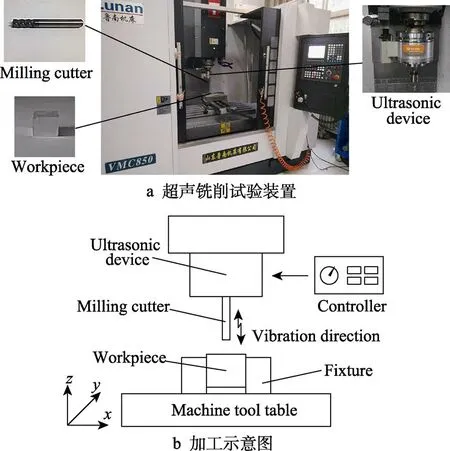
图1 超声铣削试验装置及加工示意图Fig.1 Ultrasonic milling test device and processing diagram:a) the device of ultrasonic milling; b) processing diagram

电化学腐蚀试验在电化学工作站（Zahner，札纳德国）上进行，采用对电极（Pt 电极）、参比电极（饱和甘汞电极）和工作电极（超声铣削镁合金试样）的三电极系统[13]，见图2。腐蚀介质采用磷酸缓冲溶液（Phosphate Buffer Saline, PBS），PBS 组分如表3 所示。试件的非加工面用环氧树脂密封，并用铜线引出，留下工作面积20 mm×20 mm。待开路电位相对稳定后，开始测试极化曲线，扫描电压为–0.1～0.1 V，扫描速率为2 mV/s。测试完成后，通过Zahner Analysis软件对曲线进行拟合，得到腐蚀速率（WV）、自腐蚀电位（Ecorr）和自腐蚀电流密度（Jcorr）。最后，利用扫描电镜（SEM, VEGA 3 SBH）观察试件加工面的腐蚀形貌。

图2 电化学测试装置Fig.2 Electrochemical device

表3 PBS 磷酸缓冲溶液组分Tab.3 Components of PBS g/L

1.2 方案

根据文献阅读和前期预实验的研究，选取主轴转速n、进给量f、铣削深度aP和振幅A4 个工艺参数进行超声铣削试验[14]。其中，n为1000～7000 r/min,f为0.016～0.048 mm,aP为0.15～0.45 mm。通过输出电流I（0～0.2 A）改变振幅A，空载电流1 A 对应振幅15 μm，试验过程均用超声电流表示振幅。试验基于RSM 选用CCD 方法设计，考虑4 因素3 水平进行30组试验（含6 组重复试验），试验方案如表4 所示。试验前，先将AZ31B 镁合金用带锯机（MJ3971×350）处理成20 mm×20 mm×20 mm 的立方块，再对每个试件进行0.5 mm 的预铣削，减小铣削深度产生的误差，使表面状态一致。试验后，测得试件Ra、HB 和WV值。试验流程如图3 所示。

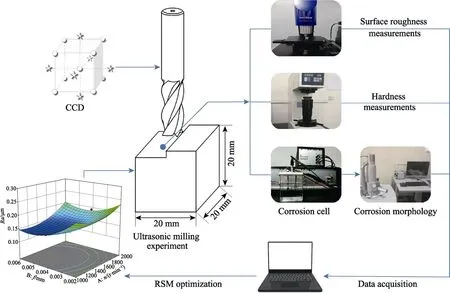
图3 试验流程示意图Fig.3 Experimental flow diagram

表4 试验因素和水平Tab.4 Experiment factors and levels

2 结果与讨论

2.1 试验结果

按照上述试验方案进行试验，得到Ra、HB 和WV的数值，结果见表5。

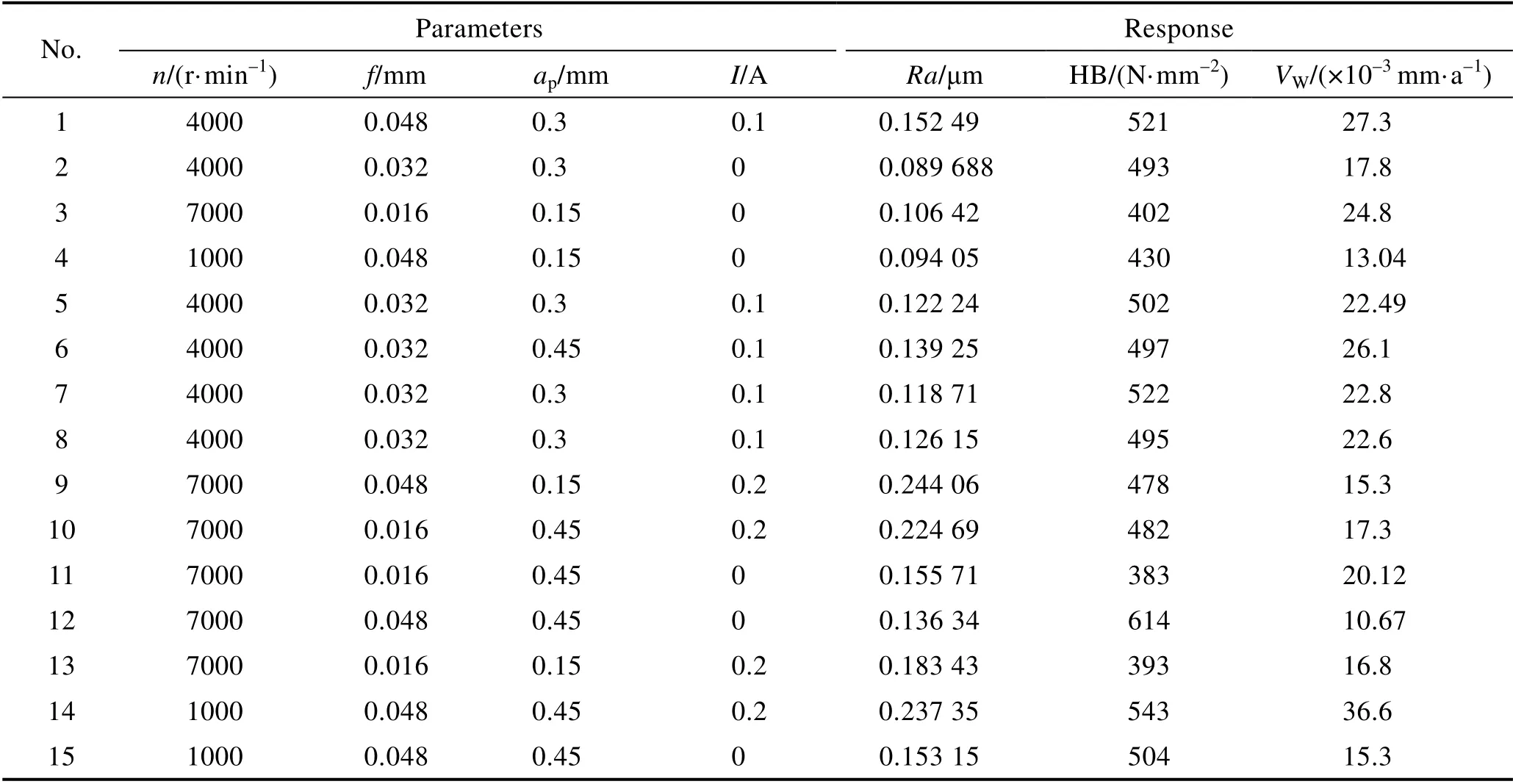
表5 试验方案及结果Tab.5 Experimental scheme and results

2.2 RSM 模型及方差分析

RSM 用于确定多因素-多响应之间的关系。通过二阶RSM 模型可以评价相关工艺参数（即输入因子）对工艺特征（即响应目标）的影响规律[15]，构建输入因子与响应目标之间的二阶数学预测模型为：

续表5

式中：0β、iβ、ijβ、iiβ为模型系数；1x、x2、3x、x4为输入因子；ε为误差。

为得到超声铣削工艺自变量（n、f、aP、I）对因变量（Ra、HB、WV）的影响规律，建立输入因子与响应目标之间的回归模型，利用最小二乘法得到二次响应曲面方程，并进行方差分析（ANOVA），进一步评估模型的有效性。得到Ra、HB 和WV的多元二阶预测模型为：

对Ra、HB 和WV的预测模型进行方差分析，结果见表6—8。F值代表整个回归方程模型的显著性，P代表回归方程模型的显著性水平。自变量数目为14，自由度为15，查F检验（F-test）临界值表，给定显著性水平的标准F值为F0.05(14,15)=2.424，3 个回归模型的F值分别为11.45、9.20 和9.58，均大于2.424，且P值全都小于置信系数0.0001，表明模型的可信度较高[16]。因此，此多元二阶回归模型可靠，可用来描述输入-输出二者间的关系。分析表6—8 中n、f、aP和I对应的P值、F值可知，对于Ra，P值由小到大依次为P(I) ＜P(aP) ＜P(n) ＜P(f)，F值由小到大依次为F(I) ＞F(aP) ＞F(n) ＞F(f)，由此可得，对Ra影响最大的参数依次为I、aP、n、f；对于HB，P值由小到大依次为P(aP) ＜P(f) ＜P(n) ＜P(I)，F值由小到大依次为F(aP) ＞F(f) ＞F(n)＞F(I)，由此可得，aP对其影响最大；对于VW，P值由小到大依次为P(n) ＜P(I) ＜P(f) ＜P(ap)，F值由小到大依次为F(n) ＞F(I) ＞F(f) ＞F(ap)，由此可得，n对其影响较大。综上所述，基于RSM 得到的超声铣削工艺参数与响应目标的多元二阶预测模型可作为Ra、HB 和WV的预测模型。

表6 表面粗糙度ANOVA 分析结果Tab.6 ANOVA results of surface roughness

表7 表面硬度ANOVA 分析结果Tab.7 ANOVA results of hardness

表8 腐蚀速率ANOVA 分析结果Tab.8 ANOVA results of corrosion rate

2.3 参数影响

2.3.1 表面粗糙度分析

图4 为主轴转速、进给量、铣削深度和输出电流与表面粗糙度之间的关系曲线，Ra为0.089 688～0.185 58 μm。由图4a 可知，提高n会使Ra值先增大后减小，田远巍等人[17]的研究结果表明，在加工过程中，塑性材料易产生积屑瘤以及鳞刺，这是由于切削速度的影响和较低的主轴转速造成的。由于切削速度较低时，切屑会产生塑性流动，且发生在刀具和切屑之间的外摩擦力增大，使作用压力加强，引起切削底层与刀具前面产生冷焊现象，产生积屑瘤和鳞刺，Ra增大。而当n超过临界值4000 r/min 时，切削温度逐渐升高[18]，热膨胀分子逐渐增加，松弛过程加快，导致工件和刀具间的摩擦系数下降，使鳞刺凸起减小。此外，n升高使镁合金的塑性形变减缓，Ra值也随之减小，这个变化趋势也与张宏基等人[19]的研究结果一致。由图4b 可知，f的增加，促使表面粗糙度值愈渐增高。其主要原因是，当f逐渐增大时，铣削热塑性作用增强，并占据主导地位，使材料的热软化程度加剧，刀尖处容易形成积屑瘤，且随其不断成长，在后刀面的挤压作用使得已加工表面有较多的材料压覆与粘结，导致Ra值增大。因此，可选择较小的进给速度以取得较为良好的表面质量。由图4c 可知，aP加深，表面粗糙度随之增大。这是因为，aP的增加易提高刀具对已加工表面的挤压作用，使得接触面积增大，铣削热增加，材料表层软化且受挤压变形，形成微观鳞刺凸起，故Ra增大。进给量和铣削深度的变化规律与文献[20]和文献[21]的结果趋同。由图4d 可知，振幅与Ra值正相关。主要原因是，振幅的增加导致机床系统振动愈发剧烈，促使应变作用增强，工件受到高应变率硬质合金刀具的冲击，导致磨损加剧，Ra值持续增大，这与文献[22]的研究结果较为吻合。

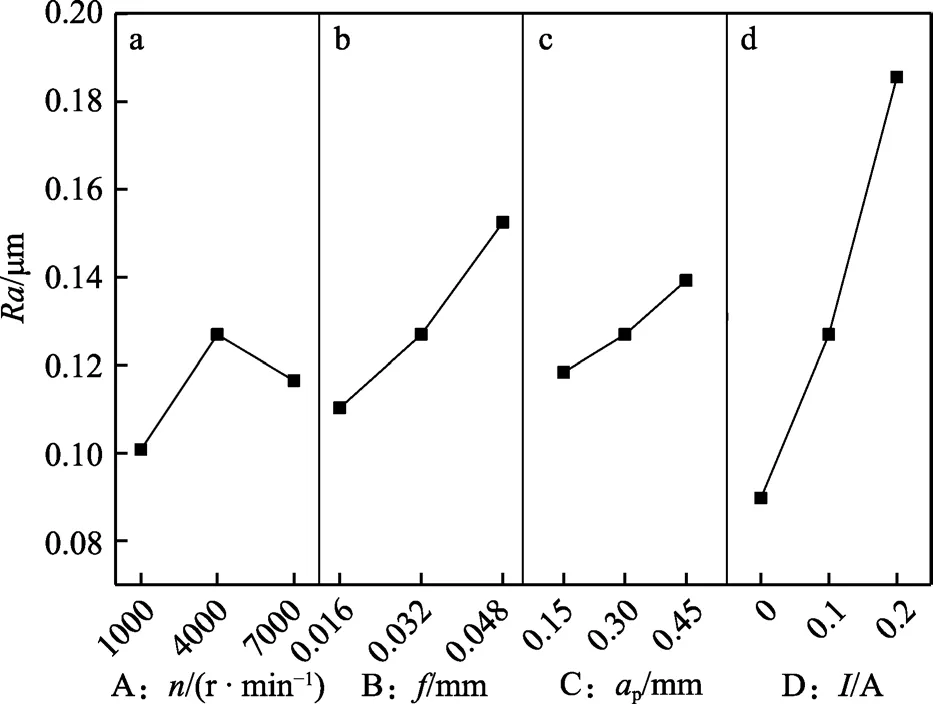
图4 不同超声铣削参数下的表面粗糙度Fig.4 Surface roughness under different ultrasonic milling parameters

改变输出电流，固定其余3 个工艺参数（n=4000 r/min，f=0.032 mm，aP=0.3 mm），得到如图5 所示的已加工表面三维形貌图。输出电流为0 A 时，测得试件表面Ra为0.089 688 μm，由图5a 可见，试件表面的轮廓曲线较为平缓，峰值与谷值之间的距离较近，且分布均匀性较好。输出电流最大（0.2 A）时，测得试件表面Ra为0.185 58 μm，由图5b 可见，试件表面的走刀痕迹较为明显，波峰与波谷处过渡尖锐且凹凸分布不均。因此，施加振幅（改变电流）后，材料的表面质量下降。

图5 不同电流下的表面形貌图Fig.5 Surface morphology under different currents

根据Ra、HB、 WV的预测方程，在确定某些影响因素的水平后，可得到其余两因素间交互作用对Ra、HB、 WV的影响规律。以工艺参数的零水平为参考，讨论输入因子间的交互作用分别对Ra、HB、WV的影响规律。由于部分交互项的P值高于0.05，这意味着交互作用显著差异小，因此只讨论交互影响较大的交互项。

图6 为n-f和n-ap两组参数的交互作用对表面粗糙度的响应曲面。由图6a 可见，当n=1000 r/min 且f=0.032 mm 时，表面粗糙度取最小值，为0.088 305 μm。由图6b 可见，当n为1000 r/min 且aP为0.15 mm时，Ra有最小值，为0.088 305 μm。这表明n和aP的减小有利于降低表面粗糙度。

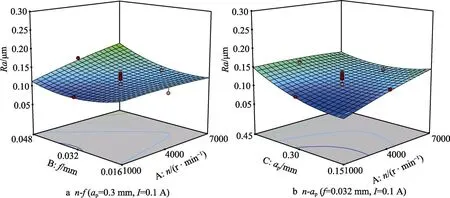
图6 表面粗糙度的响应曲面Fig.6 Multi-factor interactive response surface for surface roughness

2.3.2 表面硬度分析

图7 为不同加工参数下的HB 值，其值为47.9～54.8。由图7a 可知，主轴转速提高会使HB 值先增后减。其原因在于，n较低时，n的增加导致切削力不断增大，加工表面在机械效应作用下发生剧烈的塑性变形，使硬度有所增加。当n超过临界值时，切削温度持续递增，热效应作用变得显著，材料强度减弱，达到再结晶温度后，高温变形引起动态回复以及动态再结晶，弱化了加工硬化。由图7b 可知，f与HB 值呈正向递增关系。因为铣削过程中，f增大，则切削厚度加深，引起切削力增大，机械效应更为显著，使金属表面的塑性变形程度增大，硬化效应增强，与齐金等人[23]的研究结果相符。由图7c可知，随着aP的增加，硬度先增后减。这是因为aP增大时，由于晶粒出现滑移引起位错缠结，且在金属内部产生残余应力，使表面组织硬化，最终加工表面的强度及硬度都有些许提升。当aP的值达到0.3 mm 以后，载荷作用的加强、切削温度的上升以及残余应力的弱化使HB 值降低[24]。由图7d 可知，随着超声振幅的增大，HB 呈现逐渐增大的趋势。考虑到超声铣削过程中振动幅值逐渐加剧，后刀面与已加工面间的熨压作用增强，导致已加工表面产生明显的塑性变形[25]。

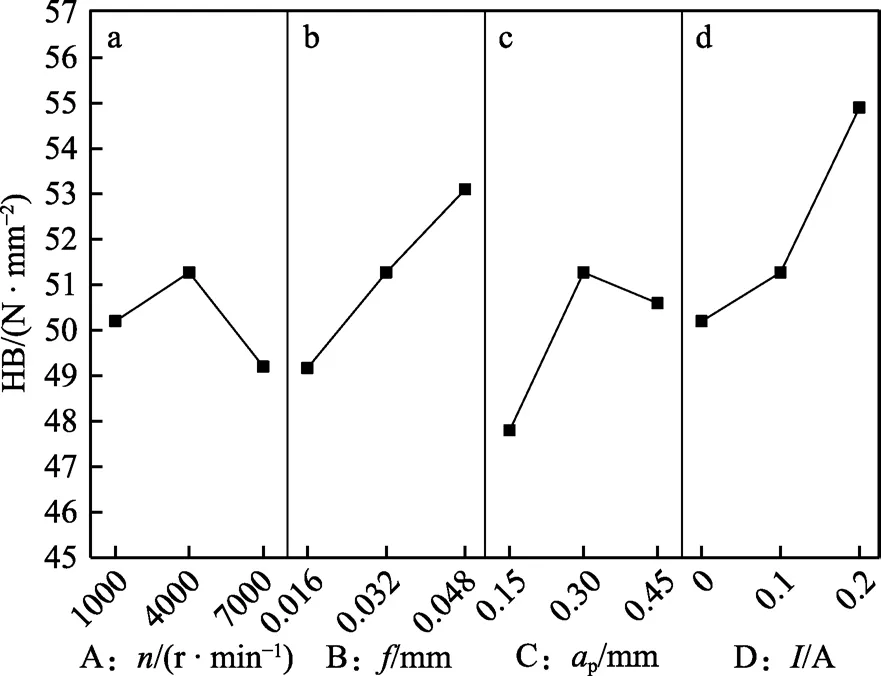
图7 不同超声铣削参数下的表面硬度Fig.7 Surface hardness under different ultrasonic milling parameters

图8 为n-f和aP-I两组参数的交互作用对硬度的响应曲面。由图8a 可以看出，当n=1000 r/min 且f=0.016 mm 时，镁合金的硬度达到最大值，为646 N/mm2，这表明要想取得较大的HB，需要较小的n和f。由图8b 可见，当aP=0.45 mm 且I=0.2 A 时，镁合金的硬度达到最大值，为646 N/mm2，在最大aP和最大I的协同作用下获得最大的HB 值。

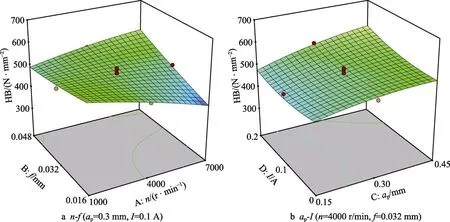
图8 表面硬度的响应曲面Fig.8 Multi-factor interactive response surface for surface hardness

2.3.3 腐蚀特性分析

图9 为主轴转速、进给量、铣削深度和输出电流与腐蚀速率之间的关系曲线。由图9 可见，WV随n的增大，呈现先增大后减小的趋势，而随f的增加，WV则是先减小后增大，aP和I的增加都会使WV增大。自腐蚀电位Ecorr和腐蚀电流密度Jcorr可以作为材料耐蚀性能的重要评判指标[26]。

图9 不同超声铣削参数下的腐蚀速率Fig.9 Different milling parameters on corrosion rate

图10a—d 分别为镁合金经不同主轴转速、进给量、铣削深度和输出电流处理后，在PBS 溶液中的极化曲线。图11a—d 分别对应图10a—d 经极化测试后镁合金表面的腐蚀形貌。图10a 为n对镁合金WV的影响。由图10a 可见，n在从1000 r/min 增大到4000 r/min 的过程中，Ecorr由–1.50 V（相对参比电极电位）负移至–1.53 V，Jcorr由2.06×10–6A/cm2增大至2.62×10–6A/cm2，当n超过4000 r/min 时，Ecorr正移至–1.52 V，Jcorr减小至–2.64×10–6A/cm2。这反映出，n增加，材料的耐腐蚀性增强。从图11a 可以看出，在低主轴转速下，镁合金表面开始有腐蚀产物析出，镁合金发生晶间腐蚀，这是因为在高电位下，细小的Mg2Zn相与低电位基体相（α-Mg）形成了微电偶腐蚀。当n继续增大到临界值时，由于已加工表面质量较差，易发生电荷转移，减小了极化电阻值，镁合金发生了大面积腐蚀，且可以观察到晶间开裂，并有许多的胞状以及块状腐蚀产物分布在表面。随主轴转速继续增大，腐蚀产物形态呈现鳞片状，产生这种现象的原因是，镁合金表面质量的改善减缓了电荷转移，使极化电阻增大，Ra值减小，这与表面粗糙度的变化规律一致。

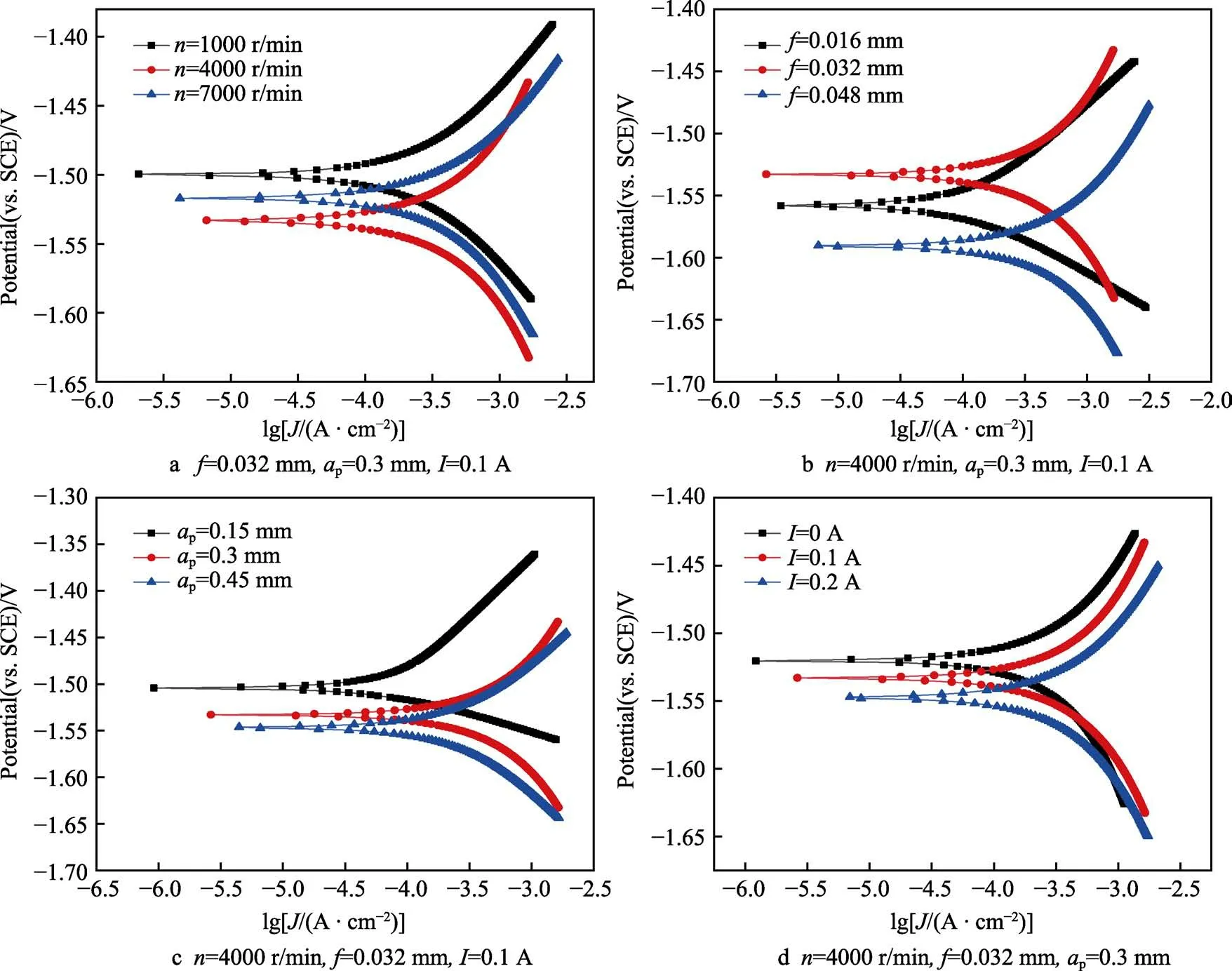
图10 不同工艺参数下的极化曲线Fig.10 Tafel curves on different milling process parameters

图11 不同工艺参数下的腐蚀形貌Fig.11 Different milling process parameters of corrosion morphology

图10b 为f对镁合金WV的影响。进给量从0.016 mm 增大到0.032 mm 时，Ecorr由–1.56 V 正移至–1.53 V，Jcorr由3.45×10–6A/cm2减小至2.63×10–6A/cm2；当f从0.032 mm 增大到0.048 mm 时，Ecorr负移至–1.59 V，Jcorr增大至6.91×10–6A/cm2。随着f的增加，材料的耐蚀性能先增强后减弱。由图11b 可以看出，f较小时，在低倍放大下观察到，有大量条状腐蚀产物附着于镁合金表面，在高倍放大下可以看到，裂纹沿晶界扩展，此时材料的晶粒尺寸较大，表面的硬度值较小，极化电阻值较大。f为0.032 mm 时，相比低进给量，材料表面的腐蚀程度有所减缓。随着f的进一步增大，镁合金发生大面积腐蚀，可以看到材料表面的凹凸较多，高倍镜下可以观察到，各晶粒之间有较大裂缝，这是由于腐蚀坑点数量的上涨且部分小坑点汇聚为大坑点，Jcorr逐渐增大，表面膜层腐蚀加速，表层氧化膜的均匀性变差[27]。

图10c 为aP对镁合金VW的影响。随着aP的加深，Ecorr由–1.50 V 负移至–1.55 V 且阳极极化电流密度由–9.16×10–7A/cm2增至4.44×10–6A/cm2，这反映出材料的耐蚀性受到抑制。当aP为0.45 mm 时，加工表面的耐蚀性能最差。从图11c 可以看出，随着aP的增加，镁合金表面开始发生点蚀，点蚀发生的部位一般为阴极相，如β 相等中间相粒子周围。随着aP进一步增大，点蚀程度加剧，发生不均匀腐蚀，可以观察到镁合金表面的局部腐蚀现象，最终形成大面积腐蚀，腐蚀产物也由开始的颗粒状向块状发展。其原因在于，随着aP的增大，切削力渐渐增大，进而产生的切削热增多，因刀具挤压于已加工表面，强化了刀具振动作用[7]，使表面粗糙度值增大，硬度值先增后减。因此，镁合金表面完整性的降低使其腐蚀速率WV增加，耐腐蚀性能降低。

图10d 为振幅对镁合金WV的影响。当施加了超声振幅后，Ecorr由–1.52 V 向负电位方向移动至–1.55 V，Jcorr由–6.11×10–6A/cm2增大至6.96×10–6A/cm2。这表明材料加工表面的腐蚀倾向性增大，腐蚀速率不断加快。由图11d 可以看出，随着振幅的增大，在镁合金表面发现裂纹且在缝隙中存在胞状和蜂窝状腐蚀产物，这些产物汇聚，造成大面积腐蚀。这是由于振幅增大，导致机床系统振动加剧，工件受到硬质合金刀具冲击时，磨损加剧，Ra持续增大。虽然硬度值也呈上升趋势，但表面粗糙度的影响大于硬度值的影响，因此主要是较大的Ra在试件表面产生微裂纹，促使氧化膜层被快速击穿，导致腐蚀加剧[28]。

图12a—c 分别为ap-f、f-I、ap-I3 组参数的交互作用对腐蚀速率的响应曲面。由图12a 可见，f=0.048 mm 且aP=0.15 mm 时，WV有最小值，为10.06×10–3mm/a，这说明要想取得较小的WV，需要较大的f和较小的aP的协同作用。由图12b 可见，f=0.048 mm且I=0 A 时，WV有最小值，为10.06×10–3mm/a，说明在最大f和最小I的协同作用下，可获得最小的WV。由图12c 可见，aP为0.45 mm 且I为0 A 时，WV最小。

图12 腐蚀速率的响应曲面Fig.12 Multi-factor interactive response surface for corrosion rate

3 试验验证

以n、f、aP、I的各工艺参数的阈值为约束条件，以响应目标Ra、HB 和WV为目标函数，优化目标为Ra和WV值最小，HB 值最大。用最小二乘法求解二阶预测模型进行优化分析，得到理论最优解如表9 所示。将表9 中的工艺参数组合作为可行工艺参数组合的一个试验方案。

表9 表面粗糙度、硬度、腐蚀速率的最优加工参数Tab.9 Optimum processing parameters of surface roughness, hardness and corrosion rate

表10 为最佳工艺参数组合下表面粗糙度、表面硬度及腐蚀速率的测量值和预测值的误差计算结果。分析试验结果可知，Ra和HB 的预测值和试验值的误差均低于5%，WV的预测值和试验值的误差低于15%，预测值与试验值的一致性良好，试验结果符合参数优化要求。

表10 表面粗糙度、硬度、腐蚀速率的预测值和试验值误差计算Tab.10 The error of predicted value and measured value of surface roughness, hardness and corrosion rate

4 结论

本文基于RSM 采用CCD 的试验方法对AZ31B镁合金进行超声铣削试验，并在PBS 中进行电化学腐蚀试验，建立了工艺参数（n、f、aP、A）和响应目标（Ra、HB、WV）之间的预测模型，对其进行显著性分析，并探讨了4 个因素与3 个响应之间的变化规律，确定了超声铣削的最佳工艺参数组合，并进行了试验验证。结论如下：

1）预测模型的精度较高，由模型的ANOVA 分析可知，超声铣削工艺参数对Ra的影响次序为I＞aP＞n＞f，n-aP的交互作用对Ra的影响最显著；对HB 影响最大的因素为aP，n-f的交互作用对其影响最显著；对WV影响最大的因素为n，f-I的交互作用对其影响最显著。

2）AZ31B 镁合金的腐蚀性能与表面粗糙度的变化规律密切相关。主轴转速的递增使镁合金的耐蚀性由弱到强，而进给量的变化规律与之相反；aP逐渐增大时，Ecorr逐渐向负极移动，且Jcorr呈现出增大的趋势。振幅增大导致表面粗糙度增大，加剧了已加工面的腐蚀。

3）最佳工艺参数组合为：n=6920.75 r/min，f=0.044 249 8 mm，aP=0.384 858 mm，I=1.077 59×10–6A。

4）通过试验验证最优加工参数组合，发现Ra和HB 的预测值和试验值的误差小于5%，WV的误差小于15%，预测值与试验值的一致性较好。