基于单目摄像机的光学立体标定技术

褚鑫磊，隋国荣

（上海理工大学 光电信息与计算机工程学院，上海 200093）

引言

双目立体视觉测量是一种非接触、实时、高精度的三维测量技术，在非接触测量、机器人导航、在线监测等领域得到了广泛的应用[1-4]。利用视觉方案对不同尺寸的目标进行非接触的高精度测量是光学工程领域的研究方向之一。摄像机的光学参数标定在光学测量和计算机视觉等许多应用中都起着重要的作用。

光学标定的任务是确定图像点的二维坐标与物体的三维世界坐标之间的关系。摄像机标定方法主要有：传统标定方法[5]、自标定方法[6]和主动视觉标定方法[7]。双目图像采集类型分为3 类：双摄像机模型[8]、单摄像机动态模型[9]、单摄像机镜像模型[10]。

通常，双目立体视觉系统需要通过采集不同角度的图像才能进行标定，然而，在现实中很难找到内参完全一样的两个摄像机，摄像机的内参数不同将影响系统的测量精度。2019 年，Chai 等[11]提出了一种单摄像机镜像双目视觉系统的标定方法，但该方法标定精度会受到景深变化的影响。2019 年，殷晨晖等[9]使用单摄像机和高精度的电动平移台构建了三维视觉系统，减少了相机内参不同对标定精度的影响。

双目立体视觉测量系统的关键指标是精度，而光学标定的精度对测量系统的精度影响最大。2001 年，张正友提出了一种灵活的标定方法[5]，所有参数的最终值是经过非线性优化后得到的，其目的是最小化平均重投影误差。这些标定算法是通过一个超定线性方程组来估计一个初始的封闭解，主要区别在于对初始解的估计和非线性优化过程。通常，目标是最小化像素坐标的误差。例如，经典方法中广泛使用均值重投影误差[12]，它表示的是真实图像坐标与根据标定结果计算得到的重投影图像坐标之间的误差。目前双目标定的优化方法几乎都是基于二维图像平面进行的，而实际的视觉测量是在三维世界坐标系中进行，优化和测量之间不同的参考坐标可能会导致标定精度下降。

2014 年，Cui 等[13]提出了双目视觉系统的精确标定方法，该方法在三维世界坐标系下，通过最小化重建点与真值之间的误差，并结合极线约束对参数进行优化。2015 年，Jia 等[14]提出了一种基于主动视觉和垂直度补偿的内参校正方法。该方法消除了摄像机运动不垂直对标定精度的影响。2016 年，Poulin-Girard 等[15]研究了不同标定条件对重构质量的影响，结果表明，平均重投影误差不应该总是被用来评估标定过程的性能，低质量的特征检测并不一定导致高平均重建误差。2018 年，Gai 等[16]提出一种基于重构误差的标定方法，在耦合程度较小的情况下，计算了摄像机之间的相对位置关系，计算出精确的三维坐标，利用重建结果的平均误差对参数进行评估和优化。Liu 等[17]致力于减小三维重建特征点与真值之间的误差，基于重投影误差、共线约束等多种约束提出了一种高精度、鲁棒性强的双目摄像机标定方法。

本文构建了一种基于单摄像机的平行双目视觉系统。通过控制高精度位移平台移动单摄像机，从而实现立体视觉；计算左、右摄像机位的初始参数，引入质心坐标法计算两摄像机间的旋转平移矩阵；利用三角剖分重构标定点的三维坐标，计算重构坐标与真值间的重构误差；通过最小化重构误差来优化标定参数。与传统方法相比，本方法在精度和鲁棒性上得到了明显提高。

1 系统原理与结构

1.1 摄像机成像模型

摄像机的成像透镜将三维点投影到二维像平面上，这种投影可以用摄像机模型的图像变换来描述。采用常用的针孔模型对摄像机进行建模[5]，世界坐标系上的物点Pw=(Xw,Yw,Zw)T到左、右摄像机的图像投影点pl=(ul,vl)T和pr=(ur,vr)T（l、r 分别代表左、右）之间的坐标变换关系如下：

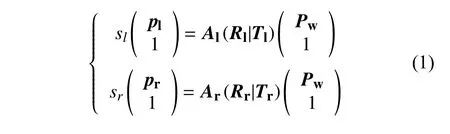
式中：sl、sr分别为左、右相机的尺度因子；Al、Ar分别是左、右相机的内参矩阵；Rl、Rr和Tl、Tr分别表示左、右相机的旋转矩阵和平移矩阵。式（1）中Al、Ar又可表示如下：

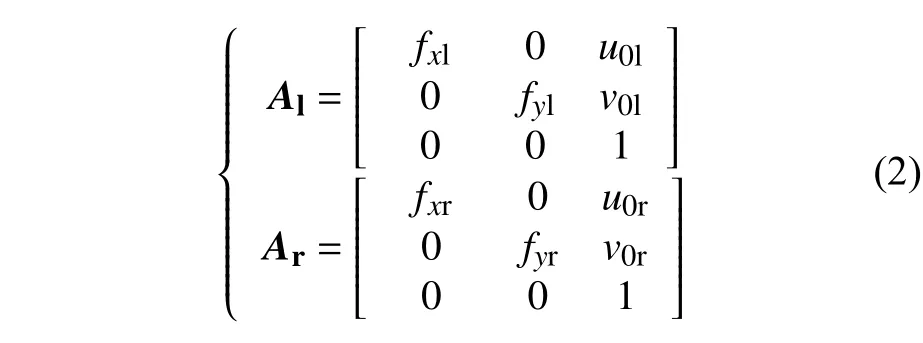
式中：fxl、fyl和fxr、fyr分别为左、右相机在x、y方向上的焦距；(u0l,v0l)、(u0r,v0r)分别为左、右相机的主点坐标。

由于相机透镜自身特殊的球形形状以及相机装配误差、制造上的缺陷，导致相机产生畸变误差。使用畸变模型来处理透镜的畸变效应，只考虑径向畸变的前两项，则关系如下：

式中：pld和prd分 别为pl和pr畸 变后对应的像点；rl和rr是无畸变像点pl和pr到各自主点坐标的距离；k1l、k2l和k1r、k2r分别是左右相机径向畸变系数的前两项。

1.2 双摄像头系统模型

两个摄像机可以用常用的针孔模型进行建模，对于三维世界坐标系中的物点Pw，存在左相机系统坐标Pcl=(Xcl,Ycl,Zcl)T和右相机系统坐标Pcr=(Xcr,Ycr,Zcr)T，世界坐标与相机坐标之间的关系如下：

式中，旋转矩阵Rl和平移矩阵Tl将世界坐标系与左相机坐标系联系起来，根据式（4），可以得到关系如下：

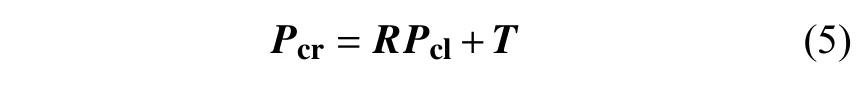
式中：R=RrRl−1为旋转矩阵；T=Tr−RrRl−1Tl为平移矩阵，表示左右相机坐标系之间的关系。在不失一般性的前提下，可以将物体三维坐标统一到左相机坐标系中，可以得到关系如下：

式中：I为一个3×3 的单位矩阵，0 为一个3×1的全0 矩阵。

通过张氏标定法[5]计算出两个相机的初始参数，建立两摄像机重投影误差之和的目标函数，该目标函数表达式如下：

式中：m为标定板上有m个特征点；n为左、右摄像机在n个不同的位置获得的n对标定板图像；为利用标定参数计算的重投影图像坐标。该参数优化方法是基于二维图像平面和通过合并两个单目系统的平均重投影误差目标函数来进行优化。

表示的是第j个标定板上第i个特征点的世界坐标，分别表示第j对图像所对应的左、右相机的外部参数，在左、右相机坐标系下对应的坐标分别为。因此，将这些参数代入式（4）和式（5）可以得到如下关系式：

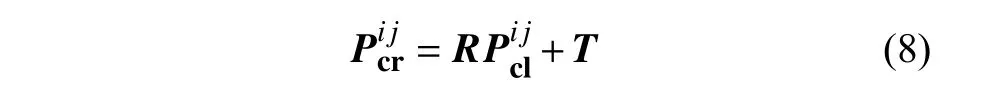
根据式（8），建立两摄像机之间位置关系的目标函数，其表达式如下：

通过最小化式（9）所示的目标函数可以估计R和T。

由于目标函数有6 个变量，并且在优化过程中很容易得到局部极小值，因此，涉及的计算过程很复杂。为了简化计算过程，本文提出了一种基于质心的计算方法。

1.3 基于质心的双目标定模型

首先分别计算左、右相机所有特征点对应的质心，然后将坐标系的原点平移到质心。和的质心坐标分别用和表示，关系如下：

将每个坐标系的原点转换成相应的质心，此时新的坐标可以转换为，关系如下：

此时，各像点之间的关系如下：

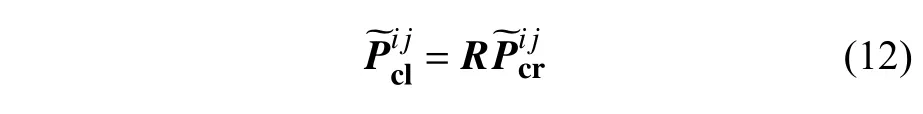
目标函数可以简化为如下:

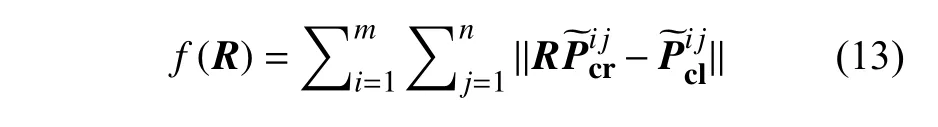
旋转矩阵R可以通过最小化目标函数f(R)得到，然后由下式：

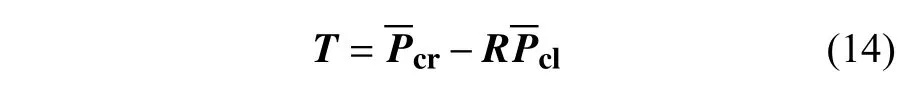
得到平移矩阵T。

1.4 基于三维空间坐标的双目标定模型

得到左、右两个图像坐标系统中的图像坐标后，需要得到三维重建的特征点。为此，利用最优三角剖分法[18]，对图像坐标pl和pr重建三维标定点，并计算特征点的空间坐标。利用式（6），将图像坐标pl和pr在左相机坐标系中重构，重构后的坐标用表示，然后将左相机坐标系的重构点转换为世界坐标。根据式（8），可得到Pw与Pclr之间的关系，其表达式如下：

将重构误差最小化，得到所有参数的最终值。为了更直观地表示标定方法的有效性，对三维重构误差进行了研究。利用平均重构误差Ew来描述标定结果的准确性，其表达式如下：

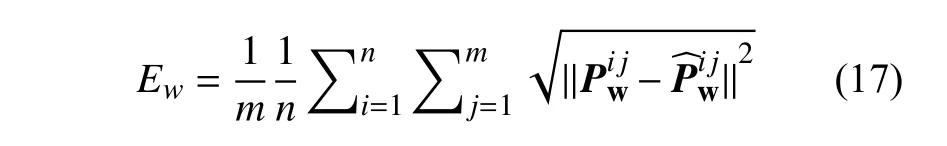
式中，Ew表示真实三维坐标与重建得到的三维坐标之间的平均误差大小。

1.5 双目立体视觉的实现

对图像坐标pl和pr重建三维标定点，将图像坐标pl和pr在左相机坐标系中重构并用Pclr表示。在重构过程中，如果两个摄像机间的内差数差别较大，会导致重建误差的增大。因此，利用单摄像机配合高精度机械结构，并通过平移或旋转实现立体视觉，使得左右摄像机参数一致，以提高标定精度。本文使用单目摄像机和电控位移平台实现双摄像机系统，这种模型是双目模型中的一种特殊情况，如图1 所示。这是一种左、右摄像机两光轴平行的平行双目系统，保证了左、右摄像机参数一致性并降低了实验的复杂度。

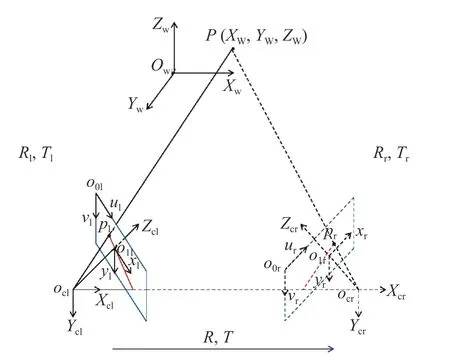
图1 单目摄像机实现双目立体视觉Fig.1 Monocular camera to achieve binocular stereo vision

2 实验设计与验证

2.1 实验系统设计

为了验证本文方法的有效性，建立了一个由单目摄像机和一维电控位移台组成的双摄像机系统。本文使用的摄像机分辨率为1 600×1 200，变焦范围为12～36 mm，像元尺寸为4.4 μm×4.4 μm，使用的标定板外形尺寸为400 mm×300 mm×5 mm，棋盘格尺寸为30 mm×30 mm，高精密一维电控位移台的分辨率为3.125 μm（8 细分下），实验装置如图2 所示。在图2 中，位置1 为左机位，位置2 为右机位，分别表示同一水平线上单目摄像机的不同位置。利用一维电控位移台，使单目摄像机在左机位与右机位间移动，从而实现双目系统。

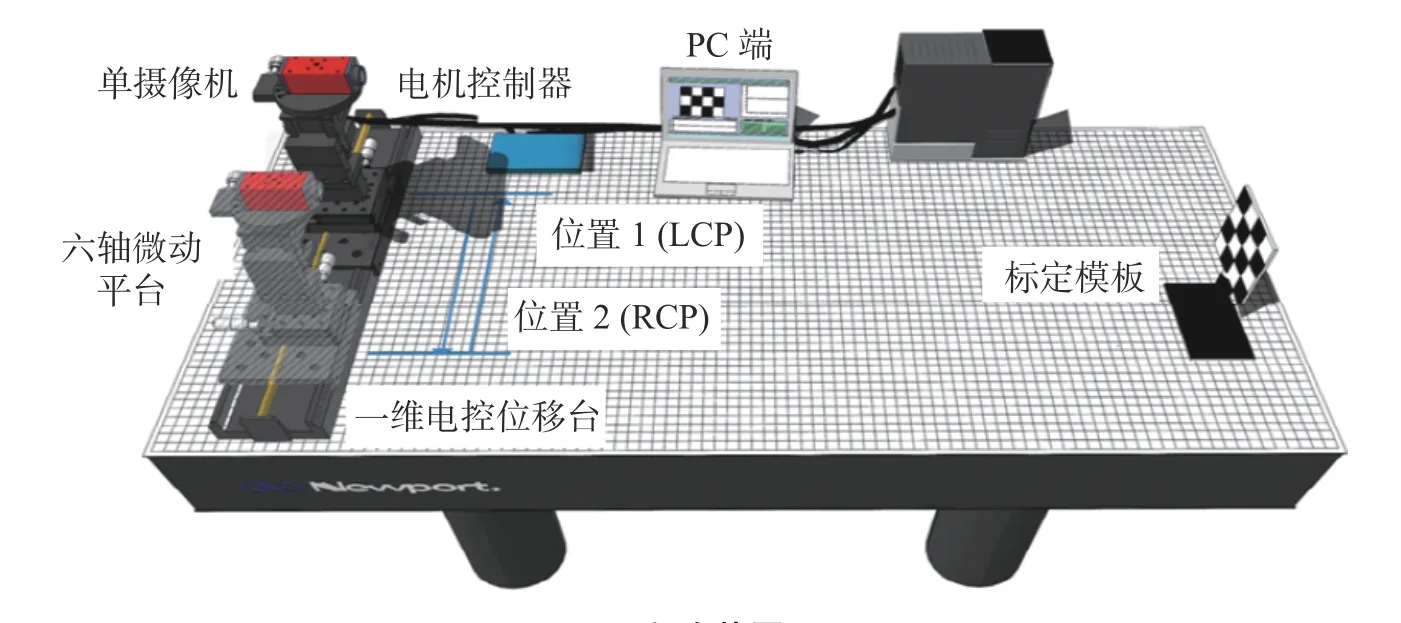
图2 实验装置Fig.2 Experimental equipment

实验步骤如下：

（1）将单目摄像机固定于一维电控位移台上，在12～36 mm 焦距范围内随机选取一组焦距值，保持标定板位置不动。一维电控位移台的往返步数设置为20 000 步，平移的理论距离为62.500 mm。

（2）在左、右机位分别采集左、右位置的标定板图像。改变标定板位姿，再采集左、右位置的标定板图像，得到左、右位置下各20 对标定板图像，其中14 对作为训练数据进行标定，另外6 对用于测试。

（3）利用张氏标定法分别计算左、右相机的初始参数，并用质心距离增量矩阵计算出旋转矩阵R和平移矩阵T。

（4）重构标定点的三维坐标，利用平均重构误差建立优化目标函数，得到最终的校准结果。

2.2 实验结果

相机的内参数和外参数的计算结果如表1、表2 和表3 所示，表中方法1 是指文献[8]的方法，2D 是指二维 优化方法，3D 是指三维优化方法。表1 和表2 表示了用不同方法得到的内参和畸变系数，可以看出，不同的标定技术对这些参数的影响不大，因为这些参数取决于单台相机的成像传感器或光学透镜的特性。表3 表示了用不同方法得到的外参，表中rx、ry、rz是旋转矩阵R的3 个分量，tx、ty、tz是平移矩阵T的3个分量。从表3 可以看出，不同技术得到的结构参数之间的差异更明显。结构参数在非线性优化过程中起着更为重要的作用，是影响标定结果的主要因素。

表1 左相机内参数和畸变系数的比较Tab.1 Comparison of left camera internal parameters and distortion coefficients

表2 右相机内参数和畸变系数的比较Tab.2 Comparison of right camera internal parameters and distortion coefficients

表3 相机外参数的比较Tab.3 Comparison of external camera parameters

对不同方法计算得到的参数进行三维物点重构，并用散点图直观地画出每个重构后的物点与其真值的误差分布图。图3 是不同方法重构误差散点图，可以看出，经过优化和重构后，物点与其真值的误差明显减小。对不同方法获得的标定结果进行平均重构误差的计算，计算结果如表4所示。以 δxoy、δxoz、δyoz表示3 个平面上的平均重构误差，δxyz表示三维空间的平均重构误差，基于2D 和基于3D 的优化方法相较于方法1 都有较大提升，平均重构误差从0.490 9 分别减小到0.388 9 和0.284 7。

表4 平均重构误差统计Tab.4 Average reconstruction error statistics

图3 不同方法重构误差散点图Fig.3 Reconstruction of error scatter graph by different methods

为了进一步验证标定算法的鲁棒性，在图像的角点坐标上加入均值为0、标准差为0～1 像素的高斯噪声，每个噪声级为0.2。通过对每个噪声级进行25 次的独立试验，得到平均结果，如图4所示。与传统的二维优化方法相比，在标定精度方面，本文提出的三维优化方法显然占优势。

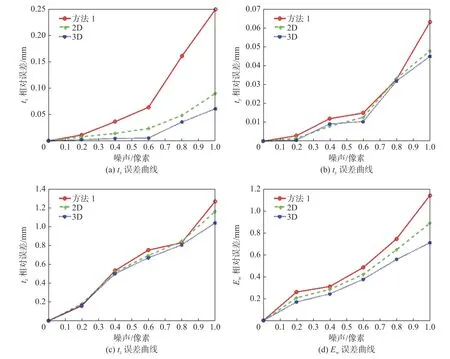
图4 平移矩阵和重构误差结果对比Fig.4 Comparison of translation matrix and reconstruction error results

对用于测试的特征点进行三维重构，得到三维重建结果，如图5 所示，图中Position1～6 表示6 个不同位姿的标定板测试图上的所有特征点进行重构后的分布图。为进一步说明优化后的标定方法的有效性，利用得到的标定结果，对得到的图像进行立体畸变校正、极线对齐、立体匹配，最后得到视差图对应的三维空间位置。根据三维空间位置与二维像素点及视差的对应关系，对目标物体进行测量。图6 是用3 种方法得到的最终视差图，可以看出，3D 优化后的视差图的特征轮廓最清晰。

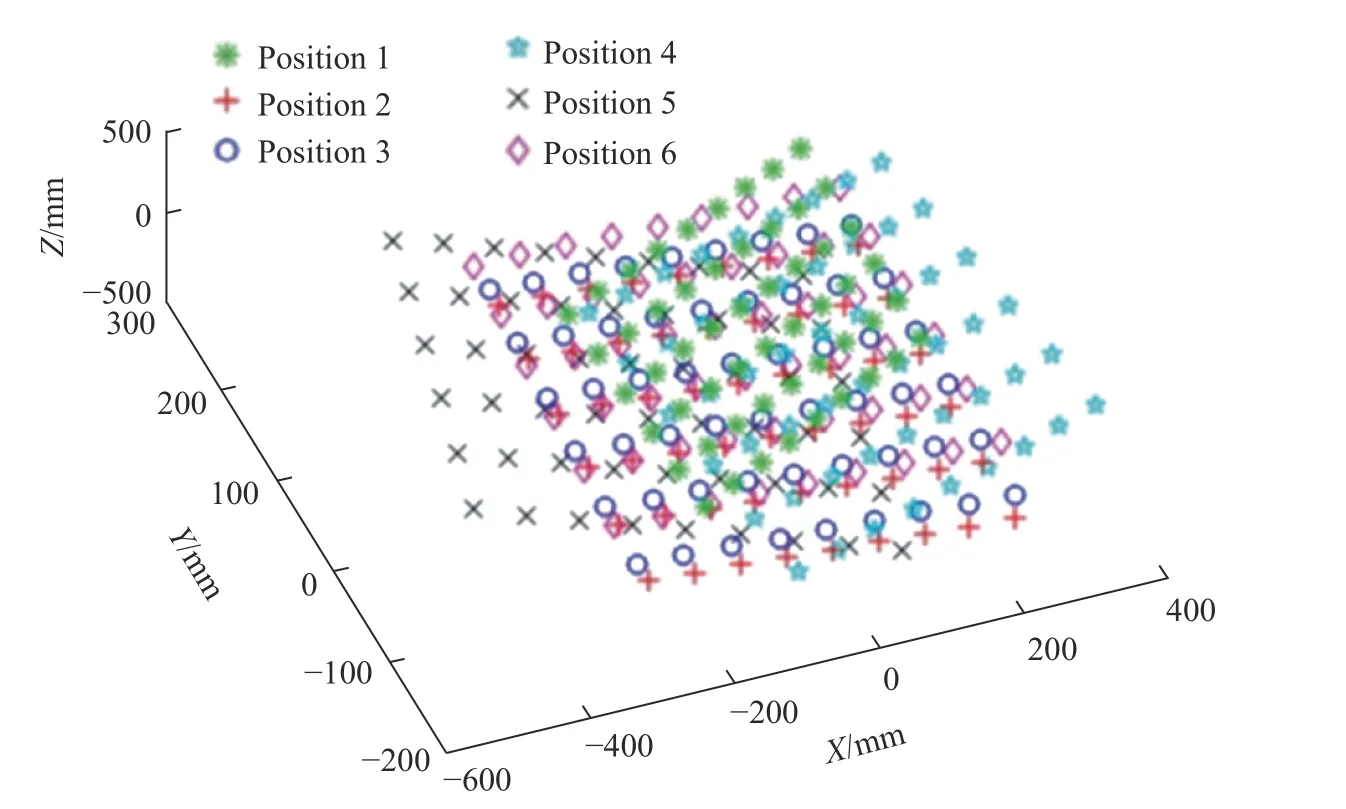
图5 测试数据的所有特征点重构图Fig.5 Reconstruction of all feature points of the test data

图6 不同方法对应的立体匹配结果图Fig.6 Stereo matching results of different methods

对3 种方法得到的视差图提取特征点，对实际尺寸为30 mm×30 mm 的方格进行测量，每种方法各进行10 次测试，得到的测试结果如表5所示。从测量结果的平均值和标准差统计中可以看出，3D 方法使测量误差从0.112 3 mm 减小到0.019 1 mm，标准差从0.183 8 减小到0.127 5，说明测量结果更加精确，波动更小。

表5 实物重构测量结果统计Tab.5 Statistics of physical reconstruction measurement results

3 结论

本文采用单摄像机和一维电控位移台实现了双摄像机系统。通过计算左、右摄像机位的初始参数，并引入质心坐标法计算两摄像机间的旋转平移矩阵。利用三角剖分重构标定点的三维坐标，计算重构坐标与真值间的重构误差。通过最小化重构误差来优化标定参数的方法。与传统方法相比，该误差直接反映了三维重构的效率，在精度和鲁棒性上得到了明显提高。研究结果表明，基于三维重构的标定误差能更加直观地提升后续三维重构的准确度，而基于单摄像机的立体视觉系统可以保证左右摄像机参数一致性。由于机械结构的限制，本方法目前还不适用于机器人导航、自动驾驶等一些实时性要求较高的任务。但是，在变焦标定领域有较广泛的应用，可为光学非接触式三维测量提供参考。