精心设计校本作业 培养学生数学学习能力

高清文

小学数学校本作业是基于学生实际情况，针对教学中的重难点而编写的适合于学生学情的学科作业。教师应发挥校本作业的针对性、层次性、时效性等优势，以学生学情和教学反馈为依据，设计出能促进学生数学能力发展的作业。

一、指向现实情境，培养知识应用能力

数学学习的根本目的之一是实现数学知识的现实应用，因此，校本作业中的数学问题如果能充分结合现实生活情境，寻找学生喜闻乐见的生活素材，便能让学生在解题时感受数学与生活实际的联系，感悟数学方法的现实应用，让他们在发现和分析问题时不断提升解决问题的能力。

如这样一道作业：姚明的身高是2.26米，腿长1.28米。有人说，姚明一步能走3米，你觉得可能吗？请你用学过的数学知识解释一下。此题考查的是学生能否应用三角形的三边关系来解决生活中的实际问题，以姚明的两条腿长组成三角形的两条边，他跨一步的距离是第三条边。因为1.28+1.28=2.56，根据三角形任意两边之和大于第三条边，所以姚明跨一步的距离一定比3米短。像这样把数学的知识点赋予一个现实的情境，培养学生用数学的眼光观察生活，能有效提高学生从现实生活中找寻数学原型的意识，从而提升知识应用能力。

二、指向学习过程，培养数学思考能力

数学教学不仅要让学生掌握基础知识和基本技能，更要让学生积累数学活动经验和感悟数学思想。在设计校本作业时，要特别重视学生对知识产生过程的理解，考查学生对问题的数学理解和思考情况，以此来诊断和分析学生的思维水平，从而有的放矢地展开教学，培养学生的数学思考能力。

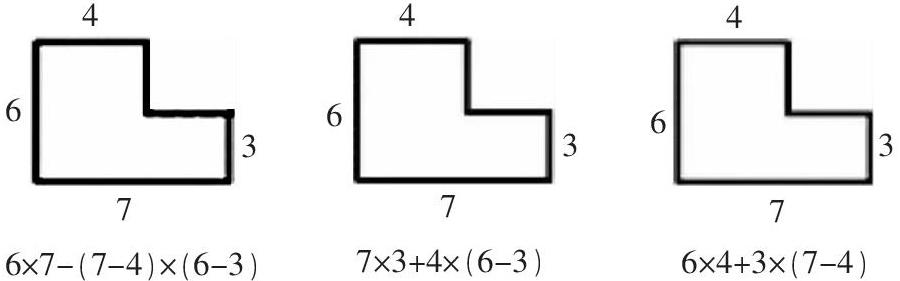
如这样一道题：求下列图形的面积，各种算法分别是怎么算的？请你用虚线表示出来。

这道题给出每个图形的面积算法，要求学生表示出每一种算法的图形分法，主要考查学生对算法背后的算理理解。这样的校本作业能显露学生探究、解决问题的过程，让学生的思维可视化，有利于教师及时了解不同层次学生对知识的学习情况，从而调整教学策略，促进学生思考能力的提升。

三、指向数学本质，培养知识理解能力

数学教学中，不仅要让学生掌握基础知识和基本技能，更要让学生理解知识背后蕴含的数学本质。因此，校本作业的设计要指向数学知识的实质性联系，促使学生聚焦知识的数学本质，以积极联想和主动迁移为途径，通过辨析、归纳、推理等方式厘清知识之间的区别和联系，自主建构螺旋上升的数学知识体系。

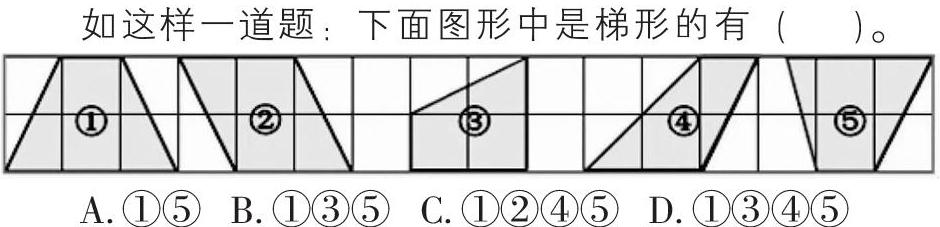
如这样一道题：下面图形中是梯形的有（      ）。

A. ①⑤   B. ①③⑤   C. ①②④⑤   D. ①③④⑤

在教学“认识梯形”时，学生头脑中的表象通常是像图①⑤这样比较“中规中矩”的标准位图，这样很容易让学生产生只有标准位图才是梯形的错觉。这道题正是针对学生的认知误区，通过对图形的变式呈现，引导学生在“变”与“不变”的辨析中聚焦概念的内涵，提升学生对概念本质的理解。

四、指向思维支点，培养说理表达能力

《义务教育数学课程标准（2011年版）》（以下简称《课程标准》）强调，数学学习要注重“四基”，培养“四能”。在设计校本作业时，应关注并体现《课程标准》提倡的能力导向，合理设计作业类型，指向学习内容的思维支点，提升学生数学综合素养。而说理正是学生表达其数学理解和数学思考的重要方式，通过学生说理情况的反馈，教师能较全面地了解学生的思维层次。

如这样一道题：将一根 10 cm 长的绳子剪两次（剪的都是整厘米），分成三段，怎样剪一定能围成三角形？（1）第一刀一定不能剪在刻度几？为什么？（2）第二刀必须剪在哪一段？为什么？（3）如果第一刀剪在刻度“3”处，那么第二刀应剪在刻度（      ）处，才能保证剪成的三段能围成一个三角形。

解决这三个问题，都要围绕三角形的三边关系这一知识点进行说理。第一刀不能剪在刻度“5”的地方，因为如果这样剪，第二刀无论剪在哪一段，那么另外两段的长度之和都会跟第一段相等，跟三角形的三边关系相违背，所以第一刀得剪在除了刻度“5”之外的任意一点。以此类推，第二刀就必须得剪在剩下的较长的那一段，这样才能满足三角形任意两边之和大于第三条边。解决第3个问题，仍然利用三角形的三边关系进行推理，不难得出第三刀只能剪在刻度“6”或“7”的地方。

本道题颠覆了传统的检测方法“给出三条线段长度，判断能否围成一个三角形”，设置的三个问题层层递进，让学生通过判断、思考、说理，进一步深刻理解三角形的三边关系。在解决这几道题的过程中，有效培养了学生运用所学的数学知识进行说理表达的能力。

五、指向开放设计，培养创新思维能力

开放性的校本作业设计可以为学生提供广阔的思维空间，引导学生综合运用所学的数学知识多角度分析问题，让他们基于自身数学经驗产生自己的解题策略。学生展现出的不同解题策略，是他们对问题的探究与理解，能有效激发他们的发散思维，也是创新意识的萌芽。

如在学习“不规则物体的体积”之前，笔者布置前置性作业：如何测量一个土豆的体积？学生在进行实验探究后，提出多种多样的方法。有的学生回答用带有刻度的量杯去测量，知道放入土豆前和放入土豆后两次水面的刻度差就是这个土豆的体积;有的回答用长方体的容器测量，知道了放入土豆后上升的水的体积就是这个土豆的体积;有的回答把土豆煮熟了捣成泥，装在立方体容器里，量出立方体的棱长，可以求出土豆的体积;有的回答可以把土豆切成一块一块，再把它们拼成近似的长方体或正方体，一样也可以求出它的体积……

开放性的作业设计，给学生提供了一个更为广阔的思考空间。最后呈现的多样化解决问题策略，既培养了学生思维的发散性与灵活性，也培养了他们的创造能力。

（作者单位：福建省厦门市同安区莲花中心小学   责任编辑：王振辉）