“三重视”为简便计算教学保驾护航

王婷婷

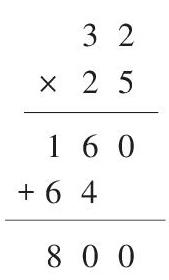
“数与代数”是小学数学的一个主要领域，而简便计算又是“数与代数”中的重要内容之一。简便计算要求学生观察算式的特点，掌握数与数之间的关系，依据四则运算定律或运算性质灵活改变运算顺序，使算式变得简便易算。这些要求看似简单，有些学生认为只需套用定律，但在实际应用过程中却并非如此。在学习运算定律之前，有的学生对四则运算还是比较熟悉的，可学习了运算定律之后，他们反而对计算题感到无所适从了。在教学过程中，教师不能把简便计算看作学生学习的一个阶段，而应把它视为一个不断渗透的过程，贯穿于运算定律学习的前前后后，让学生在一步步的积累和沉淀中逐步培养简算意识，提升计算技巧，提高运算能力。具体来说，可以从以下三个方面入手。

一、重视简算意识的培养

学生能否在平时的学习与生活中自觉地应用简便计算，很大程度上取决于其是否具備简算的意识。在大多数学生的意识里，简便计算是一种题型，而不是一种能力，题目中有要求用简便算法，才会想到采用运算定律来进行简算。究其原因，主要是学生较少体会到简便计算的价值，内心深处没有产生简便计算的需要。因此，教师要通过多种方式和途径，让学生体验简便计算的好处，感受简算的价值，让学生明白有的题目可以根据实际情况而利用运算定律进行简算，以提高自己的计算效率和计算能力。

在平时的教学中，笔者比较重视学生口算能力的训练，口算能力的培养对于学生的简算意识的养成有着一定的促进作用。这里的口算练习指的是有针对性的口算，能够凑整的计算。如1.6+3.4、2.5×0.4、125×8、78+22等。通过大量这一类型口算练习的积累，帮助学生初步建立凑整的模型，发展学生的数感。以后当学生看到78+57+22或25×14这样的题目时，自然而然地就会想到把78+22、25×4这样的数凑在一块，由此自觉地使用简便算法。当然，在对学生进行计算训练的过程中，教师应当注意不同年级的训练侧重点有所不同。低年级主要训练100以内的数凑成整十数;中年级主要训练凑成整百整千的数和小数凑成整数;高年级主要是分数凑成整数的口算。

在日常教学中，通过这样的专项训练，学生在脑中对数与数的关系会有清晰的认知，从而在解决问题时能自发地调动头脑中已有的凑整模型，让能够凑整的数先行计算。当学生从这样的凑整过程中看到计算的方便快捷后，就能感受到简算带来的好处，从而达到自觉简算的目的，逐步让技能上升为意识。

二、重视定律的学习渗透

虽然说简便计算是在人教版四年级下册开始让学生系统学习（以运算定律的学习为标志），但由于简便计算可以有效地发展学生对数的意义及运算意义的理解，盘活学生的运算思路，增强学生的数感，所以在各年级的教学中都有所体现。教师如果能在学生系统学习运算定律之前经常把这部分知识提前渗透进学生的学习中，那么学生就会随着时间的推移，积累丰富的数学活动经验。这种学生亲历的学习体验，必将潜移默化地影响学生的后续学习，带来积极的正迁移。

如教学“笔算两位数乘两位数”的内容，有右图这样一个算式，笔者在讲解算理时，让学生充分沟通计算过程的每一步算的是什么。师生最后得出结论：32×25表示25个32相加，在计算时先算5个32是160，再算20个32是640，最后把两个部分的结果相加，也就是把25个32拆成5个32和20个32两部分。这里就蕴含着乘法分配律的运用。

等到四年级学习“乘法分配律”时，笔者安排如下教学环节。首先出示一道题：一个排球25元，体育老师先买了40个，后来又买了4个，一共用了多少钱？学生列出两个不同的算式：25×（40+4）和25×40+25×4。他们计算后，发现两个算式结果相等，可以用等号连接，即25×（40+4）=25×40+25×4。此时，笔者提问：“除了通过计算结果可以说明这两个算式相等，还有其他方法可以证明吗？”学生回答：“25×（40+4）表示一共有44个25，可以拆成40个25和4个25，所以25×（40+4）等于25×40+25×4。”

学生从几个几的角度来分析两个算式之间的联系，实际上就是在不知不觉中调动了以前学习笔算乘法时的知识积累。乘法分配律对他们来说虽是新面孔，却是“老朋友”。由于有了此前笔算乘法关于几个几拆成几个几加几个几的渗透，学生学习乘法分配律就更容易，且印象深刻，很好地构建了乘法分配律“两积求和=和×一个数”的模型。

运算定律的学习不能局限于某一个阶段，而应该贯穿于计算教学的相应过程中，教师应当善于抓住机会适时渗透。这样的渗透越多，学生脑中储备的经验就越丰富。当他们系统学习运算定律的时候，就会有丰富的表象去完善自己的认知结构，从而使新知的学习变得轻松与深刻。

三、重视生活经验的提升

纵观人教版教材，我们不难发现，教材在教学运算定律时都是依托生活实际问题进行情境创设，通过引导学生在解决实际问题中分析比较不同的方法，让他们更为直观地理解简便计算的算理。因此，在教学中，我们应创设与生活相关的问题情境，把简便计算根植于情境中，让它成为学生理解简便计算算理的经验支撑，使得解决问题策略的多样化与计算方法的多样化相得益彰、同步发展。

如在教学“减法性质”时，笔者创设如下的日常生活购物情境：王老师带了450元钱去体育用品商店，她买了一个足球128元，又买了一个篮球172元，还剩多少钱？学生列出以下两种算式：第一种，450-128=322-172=150（元）;第二种，450-（128+172）=450-300=150（元）。随后，笔者引导学生讨论两种算法的含义，学生回答：第一种解法先求买一个足球后剩下多少钱，再求又买一个篮球后剩下多少钱;第二种解法先求买一个足球和一个篮球一共用了多少钱，再求剩下多少钱。接着，笔者引导学生对两种解法进行比较，学生发现计算结果都是150元，可以用“=”把两个算式连接起来，表示它们计算结果的相等，即450-128-172=450-（128+172）。这样便初步建立起了减法性质的模型。而在第二种解法的计算过程中，学生发现128+172可以凑成整百，而计算450-300可以直接口算，由此他们也深刻体会到简便计算的好处。

这样可以直接口算的计算过程，给学生带来了积极的情感体验，因此更易于将新知内化成学生自己的知识。今后学生面临相似的算式时，即便没有强调能简便计算的要简便计算，学生也会主动地运用减法性质去尝试进行简便计算。像这样在解决问题的过程中探究运算定律，激发学生对简便计算的需求，最后让学生感受简便计算的优势，能培养学生思维的灵活性，是提高学生简算能力的有效途径。

（作者单位：福建省福清市玉屏东方红小学）