三种组合浮囊型浮式防波堤的消浪特性对比研究

李娇娇，冀坷帆，张金凤，王玉红，马 瑞

（1.中交第一航务工程勘察设计院有限公司，天津 300220；2.天津大学水利工程仿真与安全国家重点实验室，天津 300072）

引言

浮式防波堤可分为箱板式和板阻式两种结构方案[1]，板阻式结构是在箱板式结构的下部增加阻尼结构。根据消浪机理及弹性性能，浮筒式结构属于反射型的刚性浮式防波堤[2]，但当多个浮筒进行组合后，可以形成柔性的多浮筒式浮式防波堤结构[3-6]。在浮筒结构的基础上，增加柔性网笼形成板阻式结构后，消浪效果优于传统箱板式浮式防波堤[7]。

近年来，数学模型分析得到了越来越普遍的应用，缩短了研究周期，成为了有效的分析手段[8]。浮式防波堤的研究内容主要包括结构锚链力和运动特性[9]、透射系数的影响因素，包括相对宽度、相对吃水、相对波高等参数[10-11]、波高、波陡[12]、堤宽、刚性[13]等。

本文针对中等水深的长周期波提出了多种组合浮囊型浮式防波堤（图1），其中，前两种组合型式为箱板式，第三种组合型式是在第一种的基础上改变而成的板阻式浮式防波堤，拟通过对比不同组合下的浮囊式浮式防波堤结构透射系数，得到较优的组合型式。

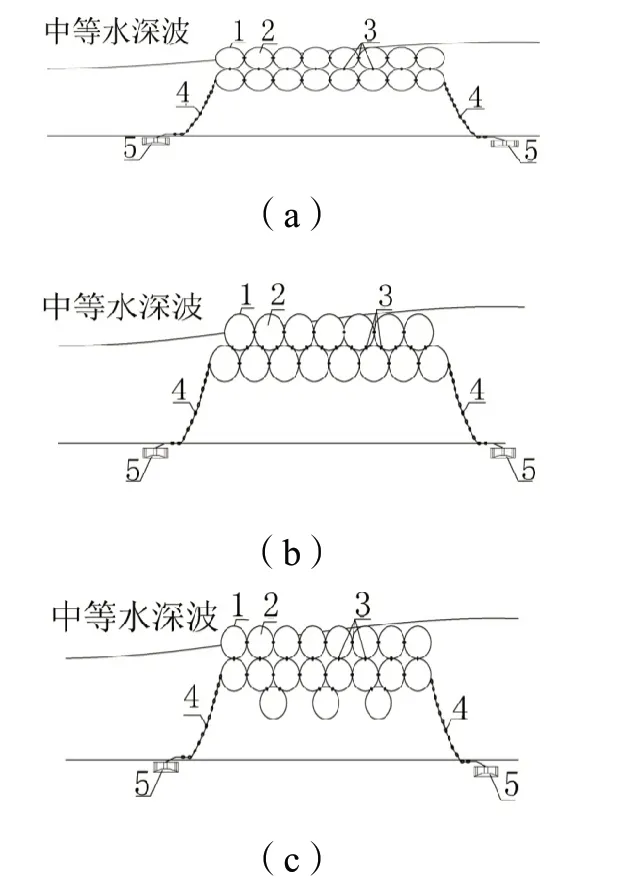
图1 组合浮囊型浮式防波堤断面图

1 数学模型的建立

1.1 模型设置

数值模型入射波浪条件为：波高2.5 m、水深15 m、周期12 s。数值波浪水槽长850 m，宽0.1 m，高28 m，建立二维模型进行波浪-防波堤相互作用数值模拟。模型中水槽网格划分共分为三部分（图2），第一部分为造波区，该区域长度取160 m，约1 倍波长，第二部分为浮式防波堤结构区，该区域长度取80 m，第三部分为波浪消减区，为防止水槽出口的边界对内部波浪的影响，该区域长度取610 m，约5 倍波长。其中，防波堤结构区需要精细模拟，因此该区域内网格较小，其他两个区域网格相对粗糙。计算网格最大尺寸为0.8 m，在水面处一个波高范围内以及浮式防波堤周围对网格加密，尺寸取为0.1 m，网格纵横比均控制在1.25 以下。

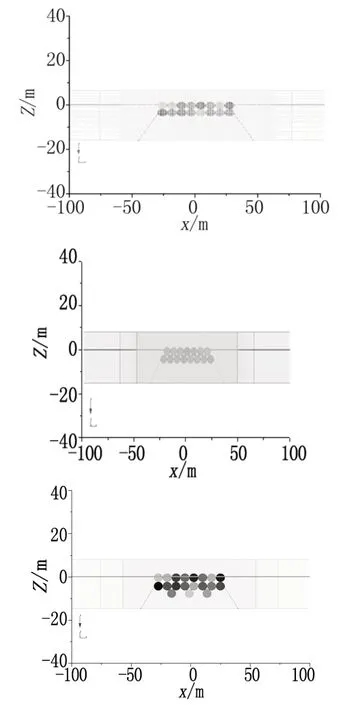
图2 数值模拟模型设置示意图

波高监测点布置在防波堤坐标为100 m 的位置处，本文中的透射系数为波浪通过浮式防波堤结构后该坐标点处的透射波高与入射波高的比值。

1.2 模型验证

为了检验模型的合理性，本文进行了不考虑结构物影响的波浪模拟，同时采用五阶Stocks 波浪理论[14]描述的入射波公式进行对比分析，理论的波面方程表达式为：

式中：k为波数；n为波浪的阶数；ω为圆频率；ηn为波形系数。

在约80s 之后，数值模拟与理论计算得到的结果（图3）匹配度很好，数值模拟的波浪场达到稳定状态。

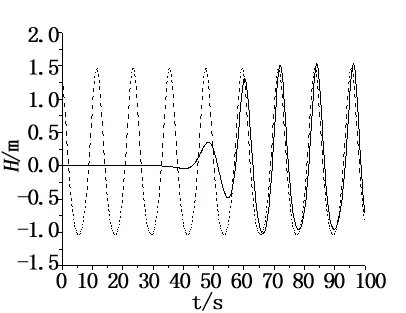
图3 数值模拟与理论计算波形对比图

为了验证数值模型的合理性，本文进行了室内试验验证。在南京水利科学研究所院的风、浪、流长波浪水槽中进行了物理模型试验，波浪水槽长175 m、宽1.2 m、高1.8 m。试验采用正态模型，按照Froude 数相似设计，模型几何比尺取为1:21。

室内试验中的浮式防波堤结构分为上、下两层，上层7 个浮囊、下层8 个浮囊。单个浮囊外径为4.6 m，整体密度为600 kg/m3。通过铰链将浮囊中心完全连接在一起，形成了一个刚性结构，单条长度4.6 m，每延米重量91.49 kg。锚固系统上部采用锚链与浮囊连接，单条锚链长度16.8 m，单延米重量47.64 kg。

本文建立了与该浮式防波堤结构相对应的二维数值模型，模型尺度与原结构相同。浮囊之间的弹簧加在浮囊中心位置，长度为4.6 m，弹性系数设为1.0e+08 kg/s2。浮囊与地面之间的锚链弹性系数设为2.4e+07 kg/s2，线性密度设为2 kg/m。

经数值模型计算得到的结构透射系数为0.65，而试验得到的结构透射系数为0.63，说明采用二维平面模型进行数值计算的方法是合理的。

1.3 工况设置

本文中提出的新型组合浮囊型浮式防波堤为柔性多浮筒式结构，在横断面方向通过柔性铰链将浮囊连接为整体，通过拖曳于海底的锚碇块及系泊于其上的锚链固定并漂浮于水体中。

为了模拟出浮式防波堤的柔性特征，使浮囊之间可以上下错动，因此，本文在数值模型计算时，将浮囊间的弹簧设置为点连接，位于浮囊壁上，长度仅为0.02 m。浮囊与海底的连接依然采用锚链进行模拟。

按照上述柔性连接设置建立室内试验断面的数值模型，经计算得到的结构透射系数为0.40，比试验得到的结构透射系数0.63 偏小，可知柔性结构通过浮囊间相互错动能够起到更好的消浪效果。

为了分析影响组合浮囊型浮式防波堤消浪特性的因素，本文建立了浮式防波堤的二维数值模型进行模拟，模型参数设置如表1 所示。

表1 数值模拟参数设置表

定义浮囊式防波堤相对吃水D/d，其中D为浮囊入水深度，即浮囊底部到静水位的距离，d为水深。相对堤宽B/L，其中B为下层浮囊宽度，L为波长。

针对相对吃水深度D/d、相对宽度B/L这两种影响透射特性的主要因素进行数值模拟。将通过单变量法分别研究分析相对吃水深度和相对宽度对结构透射系数的影响。研究工况如表2 所示。

表2 研究工况表

2 数学模型计算结果分析

本文中的组合浮囊型浮式防波堤的消浪原理主要是通过浮囊对波浪的反射和浮囊之间在水中的不规律的上下错动、左右摆动干扰水质点运动，从而消减波能。

2.1 对比相对宽度对透射系数的影响

保持相对吃水为0.433 不变（图4），随着相对宽度增大，结构方案一与结构方案二的透射系数逐渐减小，消浪效果越好，这是因为相对宽度增加后，波浪在行进过程中受扰动的范围增大，从而能量消耗越多。

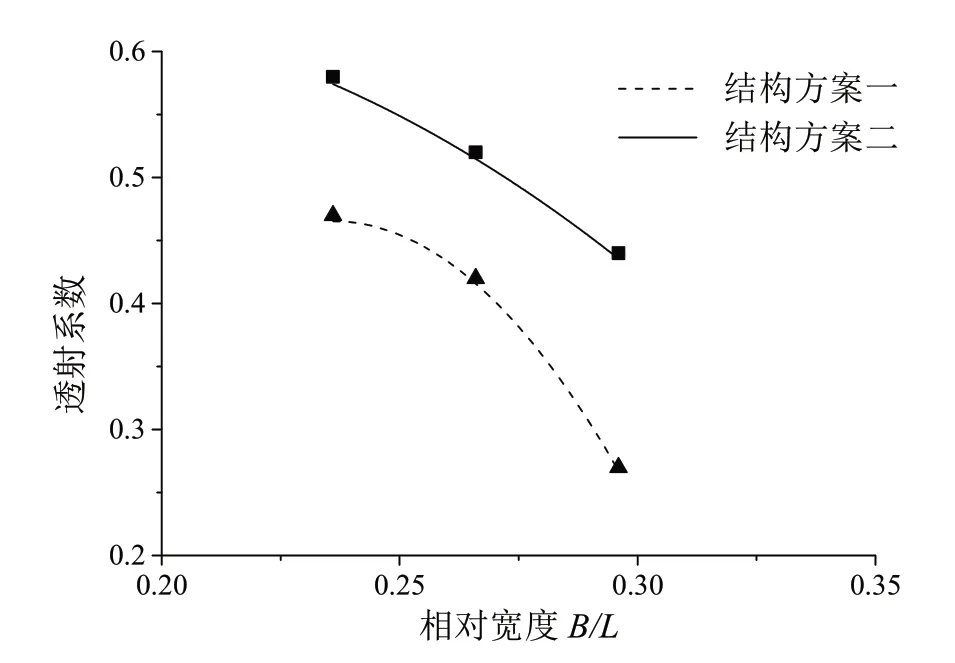
图4 相对吃水为0.433 时透射系数受相对宽度的影响

矩形组合型式的结构方案一中，透射系数与相对宽度呈可近似线性相关，当相对宽度约为0.21，结构方案一的透射系数可以达到0.5。

三角形组合型式的结构方案二中，透射系数随着相对宽度的增大而越来越陡，说明透射系数随相对宽度变化越来越敏感。当相对宽度约为0.28，结构方案二的透射系数可以达到0.5。

在同样的相对宽度条件下，相比结构方案二，结构方案一的透射系数更小，消浪效果更好，这可能是因为结构方案一在迎浪面形成直立壁，通过波浪反射消减波能，而结构方案二在迎浪面形成斜坡，波浪可以进行爬坡运动，消能效果减弱。

2.2 对比相对吃水对透射系数的影响

保持相对宽度为0.236 不变（图5），三种结构方案均随着相对吃水增大，透射系数减小，结构消浪效果越好，这是因为当相对吃水增大时，结构迎浪面的面积增大，因此能反射更多的波能。根据微幅波理论，波浪的动能大部分靠近水面，因此，当相对吃水达到一定深度后，继续增加吃水深度将不会影响波能消耗，因此相对吃水这一因素对结构透射系数的影响有限。

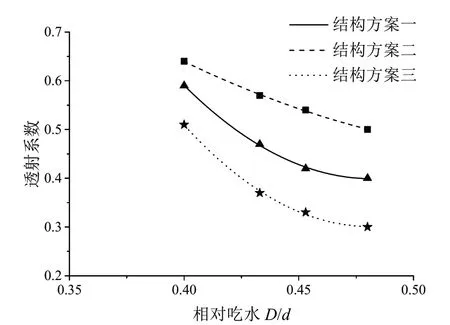
图5 相对宽度为0.236 时透射系数受相对吃水的影响

矩形组合型式的结构方案一中，透射系数与相对吃水可近似呈线性相关，当相对吃水为0.42 时，结构方案一的透射系数可达到0.5。

三角形组合型式的结构方案二中，随着相对吃水增大，透射系数减小趋势越来越缓，说明相对吃水对透射系数的影响越来越小，当相对吃水为0.47时，结构方案二的透射系数可达到0.5。

在同样的相对吃水条件下，相比结构方案二，结构方案一的透射系数更小，消浪效果更好。这可能是因为三角形布置浮囊时结构整体高度较小，在相同的吃水条件下浮囊露出水面部分较少，静水面以上部分对波浪的阻碍作用较小，因此消浪效果较差。

在结构方案一的下方间隔悬吊少量浮囊形成结构方案三的板阻式组合型式后，随着相对吃水增大，透射系数减小趋势逐渐趋于平缓。

取相对吃水相同为基准进行对比，从结果中可以看出结构方案三的透射系数比结构方案一更小，说明板阻式结构可以在箱板式基础上进一步提高消浪效果，这可能是因为下部浮囊的运动有效干扰了水质点的运动，使得波浪能量进一步被消减。

针对结构方案三，本文加入一个关于结构宽度的修正系数η，定义如式（2）所示：

其中n’为下层浮囊个数，n为上、中层浮囊单排个数，R’为下层浮囊直径，D为上、中层浮囊结构的入水深度。

可知，当下层浮囊个数n’与上、中层浮囊个数n 数量一致时，结构方案三的相对吃水可根据修正系数作如式（3）的换算，其换算结果与箱板式结构的相对吃水定义一致。

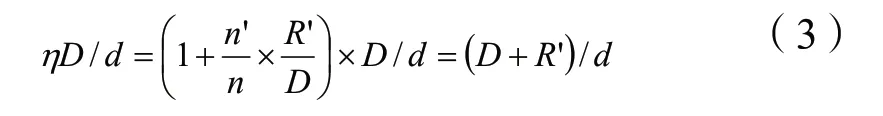
取结构方案三的相对吃水为ηD/d（图6），与结构方案一进行对比，经修正后两个方案的透射系数变化规律趋于一致，但依然难以通过一个公式表达透射系数与相对吃水的关系。这可能是因为结构方案三的组合型式除结构宽度的影响外，下部浮囊受到波浪作用后产生的横向位移可能对结构整体的透射系数也有很大的影响，因此还应考虑波浪等其他因素对结构透浪效果的影响。

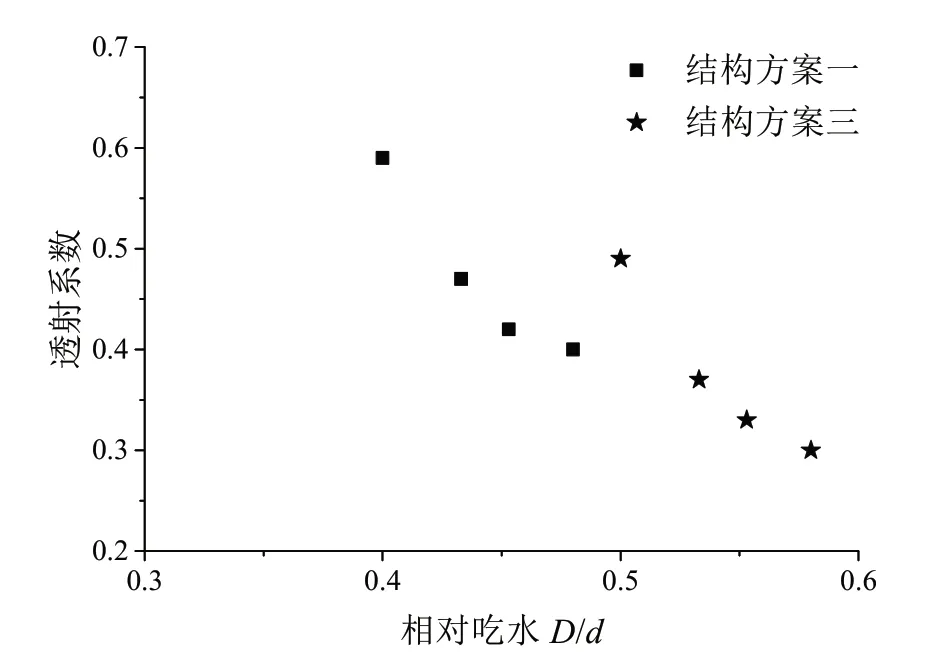
图6 相对宽度为0.236 时透射系数相对吃水的影响

3 结语

本文中提出了三种新型组合浮囊型浮式防波堤，通过不同的组合型式，该组合浮囊型浮式防波堤可以根据实际需要形成箱板式或板阻式的不同结构。文中采用Flow-3D 软件进行数值计算，在中等水深的长周期波条件下，建立了三种方案的数值模型进行分析研究，并得出以下结论：透射系数与相对吃水及相对宽度均呈正相关；矩形连接布置的结构方案一比三角形连接布置的结构方案二消浪效果更好；板阻式结构的结构方案三比箱板式结构的结构方案一、结构方案二消浪效果更好。同时，针对板阻式的组合结构，文中提出了一个关于结构宽度的修正系数，用以计算间隔布置浮囊的板阻式结构方案的透射系数，但从结果来看，除结构宽度外，其透射系数还应与波浪作用等其他因素有关。