局部热非平衡多孔介质圆管非达西强迫对流换热分析

2021-11-06岳飞龙李培超

上海工程技术大学学报 2021年2期

岳飞龙，李培超

（上海工程技术大学机械与汽车工程学院，上海 201620）

κ多孔介质由于其独特的结构和特殊的性能得到广泛关注，同时也吸引许多研究者专注于多孔介质多物理场耦合问题的发展. 在多孔介质热流耦合问题的研究中，分析研究局部热非平衡情形下多孔介质圆管或平板强迫对流对换热性能的提高具有重要意义[1−6]. 对于多孔介质平板，较多学者研究了达西流动下的换热分析. 例如，Yang等[7]研究了5种典型孔隙—流体界面的流体和固体温度分布，同时得到努塞尔数随参数变化的影响. 在Darcy线性流动模型的基础上，又有学者提出Brinkman流动模型[8]，由于其能够更好地满足多孔介质流动区域和纯流体流动区域交界面处的无滑移条件，并可说明边界之间的过渡流动，因此得到了广泛的应用[9−10]. Nield等[11]在该模型下考虑壁面恒温边界条件，研究饱和多孔介质平行平板通道内的强迫对流对换热性能的问题，得到局部努塞尔数的表达式. 除此之外，还有很多学者研究了其他不同边界条件下Brinkman流动下多孔介质平板的换热问题. 例如，Kuznetsov等[12]研究扰动流动条件下的多孔介质平板中的温度分布和努塞尔数分布，得出随着无量纲频率的增加会导致努塞尔数在幅值和相位上分布变化的结论；Cekmer等[13]提出上下壁面热流非对称边界条件下Brinkman流动下多孔介质平板的热传递特性，且定义了平板上下表面以及整体的努塞尔数分布. 在此基础上，还有许多学者考虑稀薄流体对传热的影响. 例如，Seetharamu等[14−15]分别对改变壁面热流与温度比值变化的边界条件和上下壁面均匀热流边界条件下多孔介质微平板通道内填充稀薄气体的换热进行了数值模拟，得出了相关参数对换热的影响.

同样，对于多孔介质圆管或圆环，很多研究者也研究了局部热非平衡情形下基于Brinkman动量方程的换热问题. 例如，Xu等[16]解决该模型下部分填充开孔金属泡沫的圆管中的热流交换问题，得到了努塞尔数的明确表达式；Wang等[17]得出多孔介质微环内气态滑移流下流体和固体温度分布的解析解；Xu等[18]对部分填充复合金属泡沫圆管中充分发展的强制对流进行数值研究，得到相关参数对摩擦因数和努塞尔数的影响.

在之前的工作中[19]研究了达西流动下多孔介质圆管的强迫对流换热问题，推导得出非均匀入口边界条件下的努塞尔数的解析解，并分析了相关参数对换热性能的影响. 在此基础上，本研究将分析同时基于Brinkman流动模型（即非达西流动模型）和局部热非平衡（LTNE）模型下饱和多孔介质圆管的强迫对流换热问题. 通过使用COMSOL Multiphysics仿真软件获得流体和固体温度、渗流速度和努塞尔数的数值解，并对参数如何影响多孔介质圆管的换热性能进行分析.

1 物理问题和数学模型

1.1 控制方程组

图1为多孔介质圆管强迫对流换热问题的原理图[19]. 图中：Tw为壁面温度，Tin为入口温度. 为简单起见，模型假设如下：1）多孔介质为饱和的、均匀且各项同性的介质；2）流体为稳定的、不可压缩的流体；3）忽略自然对流、扩散和辐射换热；4）忽略轴向热传导；5）流动的热物理性质不受温度影响.

图1 多孔介质圆管示意图Fig. 1 Schematic diagram of porous media circular duct

本研究利用Brinkman动量方程，并采用反映局部热非平衡现象的双温度场方程来描述传热问题. 在上述假设之下，三维圆柱坐标系下的Brinkman动量方程[20]和双能量方程[19]可以写为

式中：ϕ为多孔介质孔隙率；ks和kf为固体和流体的热导率. 符号说明见表1.

表1 符号表Table 1 Symbol table

1.2 边界条件

为求解控制方程式(1)至式(3)，对图1所示的多孔介质圆管外壁面上的无滑移速度边界和温度边界条件以及入口处的温度边界条件规定为

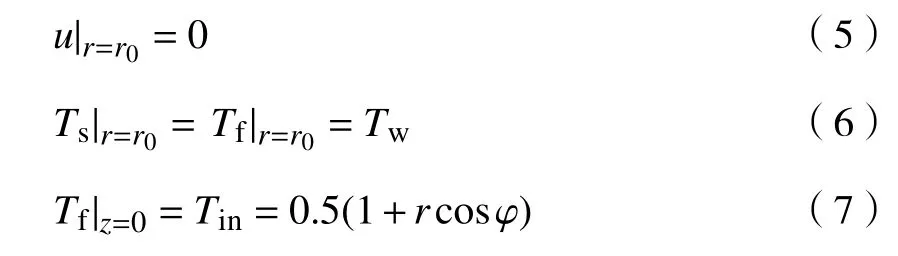
式中：r0为多孔介质圆管的真实半径；Tw为壁面温度；Tin为入口处温度.

1.3 无量纲化数学模型

为了将控制方程和边界条件无量纲化，引入无量纲变量为

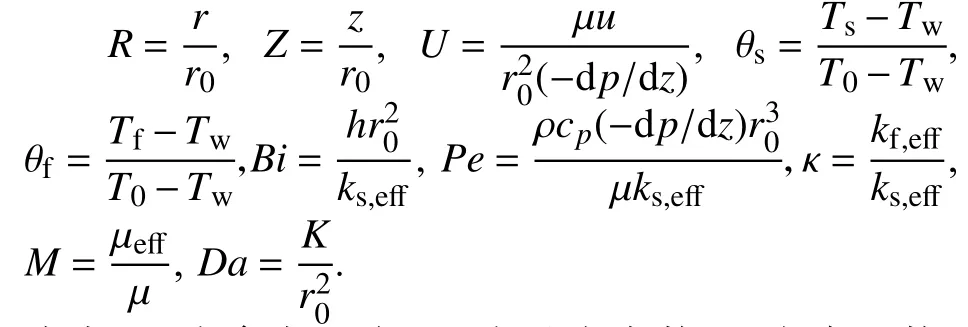
式中：T0为参考温度；Pe 为贝克来数；Bi为毕渥数，Da为Darcy数，κ为流体有效热导率与固体骨架有效热导率之比；M为流体有效动力黏度与实际动力黏度之比. 根据上述无量纲变量的定义，将控制方程式(1)至式(3)与边界条件式(5)至式(7)无量纲化，可得

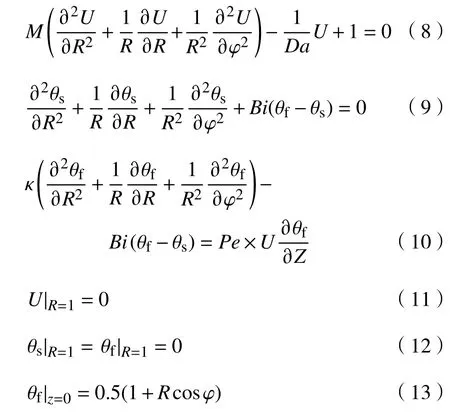
上述控制方程(8)至(10)与边界条件(11)至(13)共同组成所求解问题的数学模型. 其中未知量为无量纲速度(U)和无量纲温度(θs、θf). 物理模型中多孔介质的无量纲半径R0和长度l分别为1和5 0.

1.4 努塞尔数

努塞尔数表征壁面对流换热的强烈程度，Li等[19]推导得出壁面平均努塞尔数的计算式为

将该式输入到COMSOL Multiphysics软件中，即可求得多孔介质外表面的努塞尔数值，通过数值大小就可以判断出外壁面上对流换热的强烈程度.

2 结果与讨论

2.1 验证

经过仿真软件求解可以得到U、θs、θf和Nu. 无量纲速度和温度随坐标的变化如图2所示. 由图2(a)可以看出，U随R的增加逐渐降低；由图2(b)可以看出，双温度随φ值的增加，先减少后增加，但流体无量纲温度一直高于固体的无量纲温度；由图2(c)可以看出，温度θs和θf随Z的增加快速降低并趋于0.

图2 无量纲速度和温度随坐标的变化Fig. 2 Variation of dimensionless velocity and temperature with coordinates

为验证本研究中数值解的正确性，将Brinkman流动退化到Darcy流动的情形，并以努塞尔数随Bi变化为例，验证本文数值仿真结果与文献[19]中努塞尔数的解析解的一致性，结果如图3所示. 由图3可以看出两者具有很好的一致性. 因此，可以间接验证本文结果的正确性.

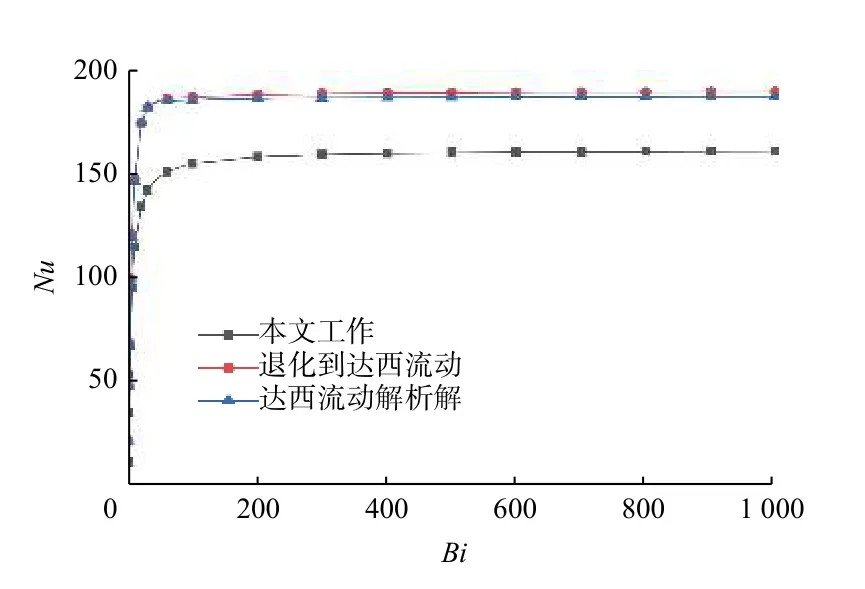
图3 努塞尔数的变化Fig. 3 Variation of Nusselt number

2.2 努塞尔数分布特性

在之后的模型中，默认M，Pe，Bi，κ及Da 分别取0.1，50，100，0.033 988，1.

努塞尔数随坐标的变化如图4所示. 图4(a)显示了Nu随坐标Z 的变化，可知当Z < 5时，Nu快速减小，随后趋于渐近值. 这意味着对流换热在入口处最强烈，随后快速减小. 这是由于对流换热的强烈程度依赖于温差的大小. 图4(b)显示了Nu随φ值的变化，为先减小后增大的余弦函数，这是由入口条件所决定的，所以壁面的对流换热强烈程度与入口边界条件有很大联系.

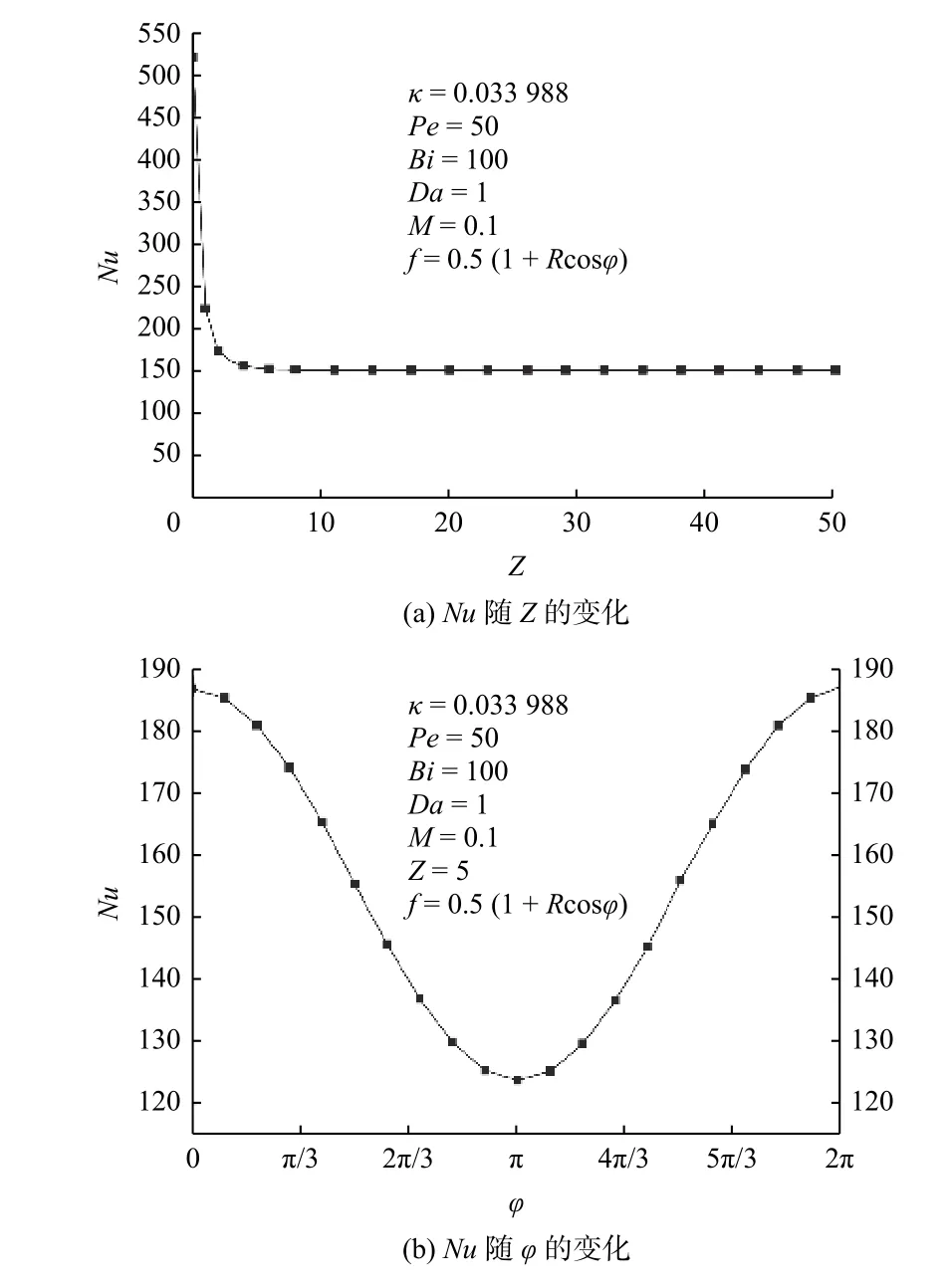
图4 Nu随坐标的变化Fig. 4 Variations of Nu with coordinates

2 .3 参数研究

2.3.1 毕渥数的影响

Bi对 Nu 的影响如图5所示. 由图可见， Nu随着Bi的增加先增加，后趋于一个渐近值. 这是因为随着 Bi的增加，流体与固体骨架之间的热交换速率逐渐变快，当Bi趋于无穷大时，LTNE模型退化为LTE模型（即局部热平衡模型），此时流体与固体快速完成热量交换，温度场控制方程也由双温度场控制方程变为单温度场控制方程. 当被退化到达西流时，Nu随Bi的变化与文献[19]中的解析解相同. 图中可以看出Brinkman流动下的 Nu要低于Darcy流动的情形，这是由于Brinkman流动考虑到了剪切能量耗散，流体流速降低，导致对流换热强烈程度减弱.

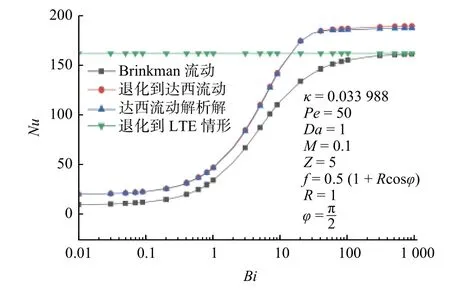
图5 N u 随B i的变化Fig. 5 Variations of Nu with Bi

2.3.2 贝克来数的影响

Pe 表征对流与扩散的相对比例，Pe 越大，就意味着对流越来越强烈. 图6展示了Nu 随Pe的变化，从图中可以明显看到Nu随Pe单调增加，这就意味着Pe越大，壁面的对流换热越强烈. 这是由于Pe的增加使管内的对流程度增大，因此加快了热量传递. 所以工程中可以通过提高Pe来增强多孔介质圆管的换热性能.

图6 N u随Pe的变化Fig. 6 Variations Nu of with Pe

2.3.3 导热比的影响

κ为流体有效热导率与固体骨架有效热导率之比. 图7展示了Nu随κ的变化. 图中可以看出，随着κ的增加，Nu逐渐下降. 这是由于随着κ的增加，固体的有效热导率相对于液体的有效热导率越来越小，固体内部导热变缓，温度明显降低. κ的增加严重影响了多孔介质圆管内温度的传递，因此Nu随着 κ的增加明显降低.

图7 Nu随κ的变化Fig. 7 Variations Nu of with κ

2.3.4 黏度比的影响

图8展示了Nu随M的变化. 图?中可以看出，Nu随M的增大而减小.M表征黏度的大小，M越大，流体黏度越大，当M趋于1时，流体速度变得极其缓慢，热量传递几乎由热传导实现. 因此，随着M增加，Nu 呈现下降趋势. 在工程中为提高热量交换程度，可以通过减小流体的M 来实现.

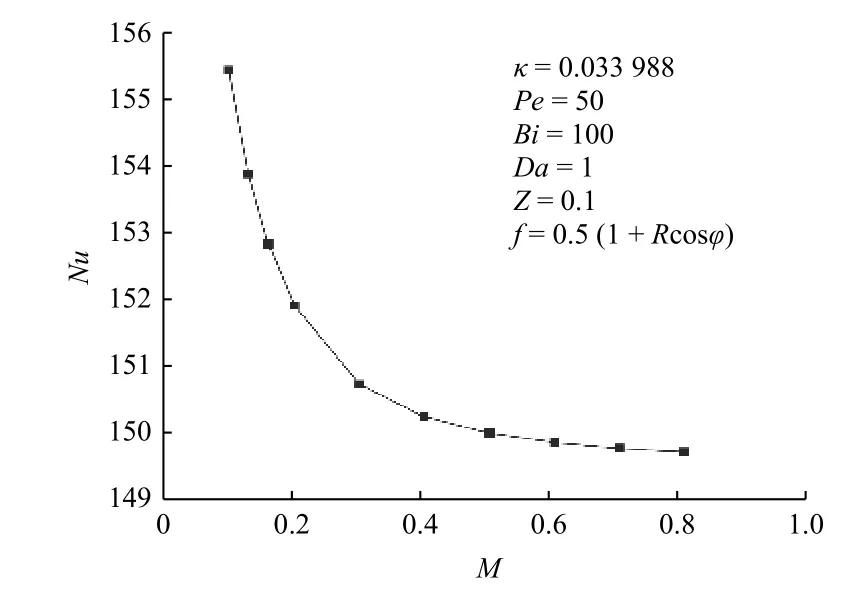
图8 Nu随 M的变化Fig. 8 Variations Nu of with M

2.3.5 达西数的影响

图9展示了Nu随Da的变化. 由图可见，随着Da的增加，Nu先增加，后趋于渐近值.Da表征多孔介质渗透能力的大小，Da越大，渗透能力越强.随着Da的增大，液体在多孔介质中渗透越快，对流增强，换热变快. 因此随着Da的增加，Nu逐渐增大. 当Da达到某个值时，Nu趋于一个渐近值且几乎不再变化，工程中可以利用此规律将Da调到合适的值即可得到较大的壁面换热效率.