核心素养下高中数学概念复习的策略

康响

摘   要：高中数学新高考注重考查学生六大核心素养，从概念复习入手，提高数学复习效率，是高中数学复习的重要策略。揭示数学概念的本质，探索考题考查的本源，强化概念固有的逻辑演绎功能，构建概念重要模型特征，是培养数学核心素养的有效途径。

关键词：高中数学概念;数学抽象;逻辑推理;直观想象

新课标倡导以人为本的教育理念，新高考命题从“知识立意”“能力立意”向“价值引领、素养导向、能力为重、知识为基”转变。在新高考背景下的高中数学复习，要顺应新课程改革潮流，紧紧围绕数学核心素养进行科学高效的数学备考复习。数学概念是高中数学知识体系的基石，是数学的逻辑起点，是培养数学核心素养重要载体。高中数学概念复习策略，是在深刻理解数学概念的内涵的同时，科学系统地拓展其外延，使数学知识脉络清淅，在培养直观想象、数学运算、数学抽象等素养方面具有极其重要的作用。

根据周期函数的定义，例2是求函数周期的问题，虽然与例1考察知识点不同，但其核心关于函数概念的考查是一致的，应当还原其概念本质，深刻理解其内涵，例2就不是单纯求周期的问题了，而是函数概念同一类题型，类似这种题就可以迎刃而解了。

许多高考题，表面上看很抽象，结果似是而非，让我们无从下手。从数学基本概念出发，还原概念本真，就可以找到解题途径，化解抽象问题，达到培养抽象思维能力的目的。

2  强化概念演绎，培养逻辑推理能力

数学概念是数学学科的精髓和灵魂，是数学思维的细胞，通过对数学概念一步步演绎推理，训练学生的解题思维能力，可以达到培养学生逻辑推理能力的目的。“定义- 方程- 性质”是研究解析几何常规手段，以抛物线为例，从抛物线的定义出发，通过“建系- 设点 - 列式 - 化简”得到抛物线轨迹方程，再通过数形结合，联立直线与抛物线方程，通过数学计算，得到抛物线内在性质及过焦点直线与抛物线的许多性质[ 1 ]。这个过程就是数学概念的演绎的过程。如果我们再进行如下的探究：

通过以上精彩的逻辑推理演绎，让学生们感受到数学美的同时，学生的逻辑思维能力进一步得到锻炼。

再探究：（3）点P是抛物线c∶y=x2-3的顶点，A，B是抛物线上的两动点，且[PA·PB][→][→]=-4。判断点D（0，1）是否在直线AB上？说明理由。

简析：本题抛物线顶点（0，-3），开口向上，D点是（0，2P），根据以上分析的结论，可得[PA·PB][→][→]=0。即D（0，1）是在直线AB上。

由此我们还可以得出更一般的结论：A，M，N点是抛物线上的点，只要满足∠MPN=90°。则直线MN一定过定点，这个点在抛物线对称轴上。

以核心概念为着眼点对数学概念层层演绎，有的放矢的探究，揭示核心概念和其他知识的思维逻辑连贯性，让学生的认知更加完整，知识掌握更加系统，而且在探究数学知识的同时，潜移默化的培养自身的数学逻辑思维能力。在辩证思维和创造性思维作用下，学生的思维能力得到不同程度的锻炼，更加准确的认识知识的形成过程。

3  构建概念模型，培养直观想象能力

数学模型对解决数学问题有直接的促进作用，把数学概念模型化，可以有效培养学生的直观想象能力。高中数学立体几何的点、线、面位置关系，线线、线面夹角，点、线、面距离，及空间几何体面积与体积等概念问题，都可以在长方体、正方体等图形中找到几何模型，引导学生把实际问题化归到概念模型，主动建立几何模型进行观察和分析，在一定程度上形成空间思维，这是培养直观想象力的基本前提。

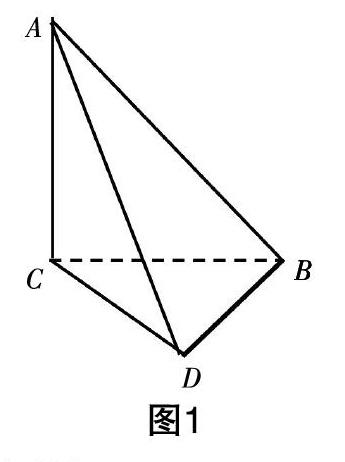
【例题4】已知AC⊥面BCD，∠CBD=90°，，AC=BC=BD（图1）。

（1）求AB与CD所成的角。

（2）求三棱锥A-BCD外接球的表面积[ 2 ]。

分析：根据条件，在已知三棱锥A-BCD的基础上，构造正方体（如图2），根据正方体的对称性质，∠EDC即为异面直线AB与CD所成角的平面角，ΔEDC是等边三角形，（1）得解。由三棱锥A-BCD与正方体的位置关系与正方体的外接球O的位置关系可知，外接球O就是三棱锥A-BCD的外接球O，此时线段AD是球的直径，AD中点O就是球心，球半径r=AD，（2）得解。

正因为正方体或长方体中，可以很直观构造出立体几何许多概念性模型，一旦这些数学问题能化归到正方体（长方体）这类模型上来，很多抽象的空间问题都可以转化到具体的直观的空间里，从而把陌生的、复杂的问题转化为熟悉的、 简单的问题，在增强学生学习信心的同时，又培养了学生的直观想象能力，发展了数学核心素养。

高中数学基于概念的复习是机遇也是挑战，数学概念的本质往往能够将问题的本质属性反映出来，再借助各种技能手段对概念外延进行深入探究，以此形成对数学概念的清晰认知。探讨高中数概念复习策略，挖掘数学概念教学的科学价值，不仅提高了教师概念教学水平，提升教师的专业素养，而且让学生亲身经历概念发生、发展过程，感受数学家思维的轨迹，促进学生对数学概念的深度理解，建构良性的数学观，有效提高学生的数学思维能力，进而实现学生核心素养的培养。

参考文献：

[1] 杨学雄.夯实基础提升能力——谈高三数学一轮复习策略[J].教师通讯，2017（14）.

[2] 胡方杰.基于直觀想象的数学核心素养的解题策略[J].中学数学研究，2020（7）.